基于幾何參數的橋式起重機主梁優化

朱 濤

(太原重工股份有限公司技術中心，山西 太原 030024)

0 前言

橋式起重機作為起重機的一種重要結構形式被廣泛應用于工礦企業，是生產作業過程中主要的裝卸設備[1]。橋架是起重機最重要的結構件，質量一般占整機自重的60%以上，而橋架的質量主要取決于2根箱形主梁的質量[2]。主梁是橋式起重機的主要組成結構件，也是整機載荷的主要承載部件，其設計參數取值的優劣對整機的設計起決定作用[3]。傳統的橋式機主梁結構設計，大都根據設計經驗或采用對原有設計圖紙進行修改的方法，這樣設計出的產品雖能滿足工程性能上的要求，但具有過大的安全系數和裕度，必然導致材料的浪費和主梁自重的增加。

實踐證明，在機械設計中采用優化設計方法，不僅可以減輕機械設備自重，降低材料消耗與制造成本，而且可以提高產品的質量與工作性能[4]。因此，優化設計已經成為現代機械設計理論和方法中的重要組成部分，并且越來越受到機械設計領域中的科研工作者及工程技術人員的重視。

本文對橋式起重機主梁結構進行幾何參數優化，使主梁的結構尺寸更加合理，減輕其自重。本文的研究對起重機設計和改進具有一定的指導意義和較高的參考價值。

1 主梁優化數學模型的建立

優化數學模型，就是用于描述優化問題的設計內容、優化意圖、變量關系和有關條件的數學表達式。數學模型是優化設計的基礎。優化數學模型包括三大要素，即目標函數、設計變量和約束條件。

在優化設計中，一個設計的優劣需要有一個指標，這個指標就是目標函數，在大多數優化中，常見的目標有重量、應力等[5]。目標函數通常是設計中變量參數的極小值，必須是設計變量的可計算函數，否則，優化會失敗或者沒有意義。目標函數的確定是優化設計中最重要的決策之一。本文主梁參數優化的目的在于使主梁的質量最輕，因此取主梁質量作為目標函數F(x)。

在對結構進行優化過程中，通過不斷調整賦值，以達到最優的獨立參數，即為設計變量。優化設計的目的就是要得到各個設計變量的最優組合。理論上任何影響目標函數的變量都可以作為設計變量，但設計變量的數量過多會使所求問題過于復雜，大大增加計算量，因此實際中設計變量的選取通常遵循的原則：從有相互依賴關系的變量中刪除非獨立變量，去除影響較小的參數，盡量減少設計變量的個數。

依據本文優化設計原則，選取該主梁的優化設計變量，包括：主梁高度、上蓋板厚度、下蓋板厚度、軌道側中部腹板厚度、另一側腹板厚度、軌道側端部腹板厚度、弧板厚度、主梁寬度、下蓋板寬度。

本文主梁優化數學模型的約束條件：(1)剛度約束條件：滿載時，主梁最大下撓小于許用值；(2)強度約束條件：滿載時，最大應力不超過許用應力。

2 有限元仿真流程自動化

本文研究的橋機主梁三維片體模型如圖1所示。要實現有限元仿真流程自動化，首先要對主梁幾何模型進行參數化。

圖1 主梁片體模型

根據橋機主梁的結構形式和受力特點，規劃和制定相應的參數化數據集，用以構建主梁的參數化框架。這些參數不僅要能夠反映主梁的幾何特點，還要能夠反映其受力特點。當參數變動時，仿真模型的各個環節都應該能夠自動變動和更新。

在有限元分析前處理中建立主梁的參數化模型草圖，如圖2所示。這些圖包括主梁的各向視圖和剖視圖，能夠充分反映主梁的形狀。最終建立的主梁模型全部參數約有130個，包括幾何尺寸參數和厚度參數。

圖2 部分主梁參數化模型圖

在主梁幾何模型參數化的基礎上，利用NX軟件自帶的API開放接口，采用二次開發的方法，實現整個仿真流程自動化。這種方法可控性強，正確性容易保證，不易出錯(NX軟件本身自帶的參數化方法也可以實現網格的自動劃分，但是經過測試，當參數改變后，有限元模型更新時容易出現部分片體網格丟失。)

仿真流程自動化包括：打開prt文件，導入表達式，更新prt模型，新建有限元仿真文件fem及sim，劃分網格，添加約束并加載(主梁有限元模型如圖3所示)，求解，打開結果文件并輸出到txt中。

圖3 主梁有限元模型

整個有限元分析流程(包括前處理、分析計算及后處理)都由計算機自己完成，不需要人工干預。這是后續實現參數優化數據循環的基礎。

3 參數優化

在通過二次開發實現仿真流程自動化的過程中，生成可執行程序文件。接著在多學科優化軟件中搭建主梁參數優化模型，如圖4所示，并調用這些可執行程序文件，進一步實現參數優化。圖4中，simcode實現以下功能：打開prt文件，導入表達式，更新prt模型，新建有限元仿真文件fem及sim，劃分網格，將主梁質量輸出到mass.txt中，添加約束并加載，求解。simcode1可實現讀取結果文件op2，并將最大位移及最大應力輸出到result.txt中。

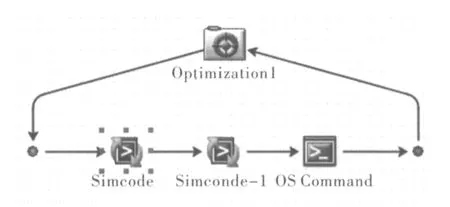
圖4 主梁參數優化模型

采用全局探索法進行優化，該方法適應性強，只評價設計點，無須計算任何函數的梯度，因此目標函數可以是多峰性、非線性、非連續、不可微函數。而且能求解全局最優解，避免了集中在局部區域的搜索。

將主梁高、腹板厚度等設計變量作為輸入，如圖5所示；主梁質量(目標函數)、最大下撓及最大應力(約束條件)作為輸出，如圖6、圖7所示。設計變量更新一次，整個仿真流程自動更新一次，從而實現循環，最終找到最優方案。

圖5 設計變量取值范圍

圖6 約束條件

圖7 目標函數

對優化模型進行求解，優化過程如圖8所示。每一行的數據為一組設計變量及相應的有限元計算結果(即目標函數和約束條件)。

圖8 優化過程

在主梁優化過程中，用戶可以對設計過程進行實時監控。目標函數隨設計變量的變化情況如圖9所示。

圖9 目標函數優化進程

主梁參數優化的優化結果如表1所示。從優化結果可以看出，在滿足約束條件的前提下，主梁質量減輕了2.67 t。

對優化后的主梁計算結果進行分析，查看優化后主梁的應力云圖和豎向位移(即下撓)云圖，如圖10～圖12所示。

優化后的主梁跨中工況最大應力為189.40 MPa，跨端工況最大應力為206.87 MPa，主梁最大下撓為34.67 mm，均小于許用值。

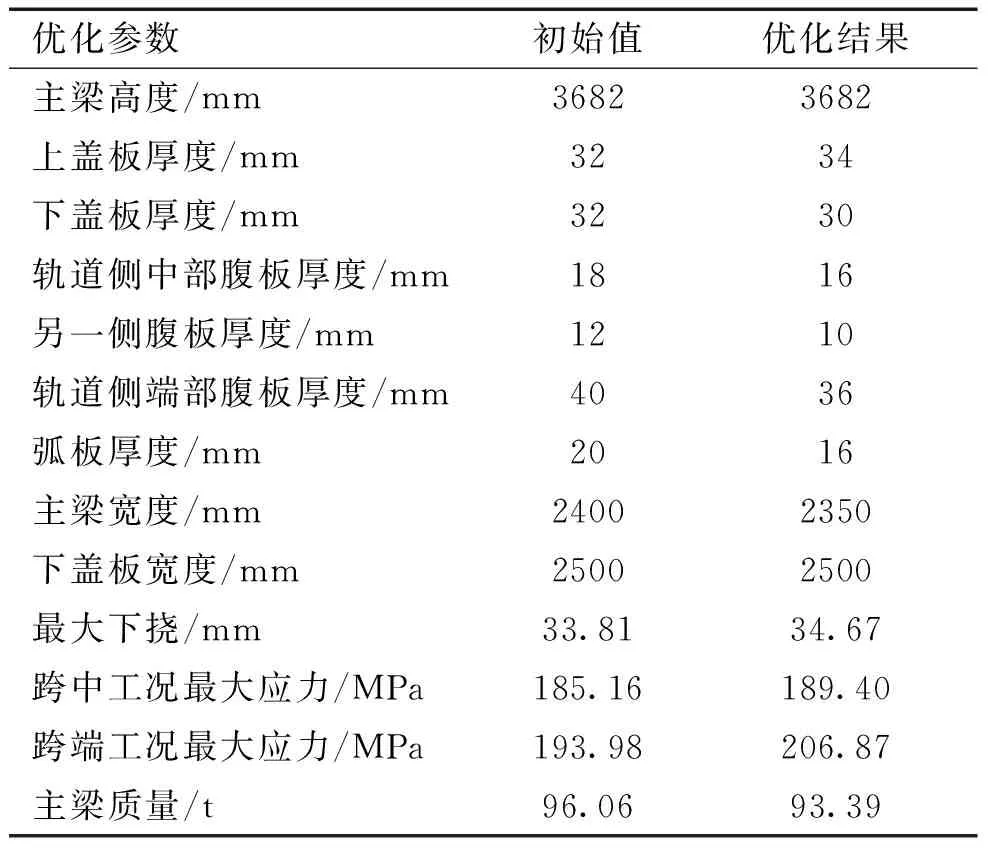
表1 優化結果

圖10 優化后的主梁跨中工況應力云圖

圖11 優化后的主梁跨端工況應力云圖

圖12 優化后的主梁豎向位移云圖

4 結束語

本文結合有限元理論及結構優化的方法對橋式起重機主梁進行分析和幾何參數優化。建立了主梁結構的優化數學模型，在主梁幾何模型參數化的基礎上，采用二次開發的方法，實現了整個有限元仿真流程自動化并利用多學科優化軟件對主梁進行了參數優化。

優化后的主梁強度和剛度均滿足要求，且質量減輕了2.67 t。從而達到了輕量化設計的目的，降低了產品成本。且優化過程不需要人工干預，縮短了研發周期，提高了生產效率。

本文的研究對起重機設計和改進具有一定的參考價值。并且此研究方法還可以推廣到其他產品的設計和優化中，應用前景廣闊。