二軸磁體的設計計算方法研究

陳 浩，林春生，賈文抖

(海軍工程大學兵器工程學院，湖北武漢430033)

0 引言

在水下磁場測控與反測控的對抗中，歷來磁場反測控的常用方法是在水下模擬艦船磁場以誘導水下磁場測控系統的觸發工作。隨著技術的發展，水下磁場測控分析系統越來越先進，對于單軸磁體模擬產生的磁場，測控系統用分軸磁場獨立分析的方法就可分辯出其是否為真正的艦船磁場。這就給水下模擬艦船磁場的反測控系統提出了更高的要求。

通過大量的分析研究和論證，仿真分析與試驗驗證均表明二軸磁體是目前水下模擬艦船磁場的最佳方案[1]。按現有設計條件要求，二軸磁體的體積和重量必須嚴格控制在指定的指標要求以內。通過設計計算和實驗研究，確定了采用同鐵芯、二繞組、同軸線、又正交的特殊繞制方法進行兩軸磁體的設計，并進行了可行性研究。

1 兩軸磁體的設計

兩軸磁體的原理結構圖如圖1所示。把同一圓筒形鐵芯做成中間段壁薄，兩端壁厚；再把螺線管繞組繞在中間段壁槽內，設計壁槽內空間正好繞滿螺線管繞組所要求的線圈匝數；然后在兩端壁厚段按圖1所示位置繞制馬鞍形繞組。這樣螺線管繞組產生縱向磁場，而馬鞍形繞組產生垂直磁場，只要馬鞍形繞組繞制時定位準確，那么二者所產生的磁場正好正交，保證了二軸相互垂直磁場的產生。繞線中的電流走向如圖中Iz所示。

圖1 磁體原理結構示意圖Fig.1 Schematic diagram of principle structure of magnet

本方案設計需要對以下3個方面進行設計計算：一是鐵芯的形式設計、材料選取和磁矩的計算；二是螺線管繞組的設計與計算；三是馬鞍形繞組的設計與計算。

2 鐵芯的設計計算

根據原單軸磁體論證指標要求，兩軸磁體總磁矩應該等于大于Mz。

圖2 部分材料的磁導率與磁感應強度的關系曲線Fig.2 Relation curve of permeability and magnetic flux density of partial materials

2.1 鐵芯材料選擇

為了盡量減小體積和重量，應優先選用磁導率高而矯頑力又小的磁性材料做鐵芯。圖2是部分材料的導磁率與磁感應強度B的關系曲線圖。圖中曲線標號對應的材質如表1所示。通過對比分析，綜合考慮后選取冷軋電工鋼做本方案鐵芯的材料，其最大磁導率可達38 000[2]。

表1 圖2中標號對應的材質Table 1 Corresponding material to labels in Fig.2

下面利用5-冷軋電工鋼的磁導率與磁感應強度的關系曲線來估算鐵芯的磁化強度M和磁化率X。為了充分發揮鐵芯的電磁效率，一般電磁鐵芯的工作點都是選在最大磁導率附近。本設計考慮兩軸不同類型的線圈共用一個鐵芯，為留有一定余量，選取工作點B＝1.3 T，則鐵芯的磁化強度M5及磁化率X分別為

2.2 鐵芯尺寸的初步估算

2.2.1 圓筒形鐵芯磁矩計算公式的確定

設圓筒形鐵芯外徑為2R，內徑為2r，長為L，則其體積V和磁矩M分別為

2.2.2 圓筒形鐵芯長細比計算公式的確定

按理論假設條件要求，圓筒形鐵芯的長細比λ等于鐵芯的長度L與橫向尺寸2R2之比，這里的橫向尺寸是電磁鐵芯最大橫截面積的圓的直徑2R2。

因為

則

2.2.3 鐵芯的磁矩估算

鐵芯的外形為中部凹槽的圓筒形，圓筒中間段的厚度為兩頭的一半，則兩頭厚的圓筒長度之和等于中間段長度，鐵芯圓筒的總體半徑為它們的平均半徑。 設圓筒形鐵芯平均外徑 2R′，內徑 2r′，長L′，代入上式計算得磁體鐵芯磁矩為

總磁矩應是鐵芯磁矩和線圈磁矩的總和，只是線圈磁矩較小，主要是鐵芯磁矩，這里設計鐵芯磁矩為Mz，計算結果表明總磁矩大于設定數值，完全滿足設計要求。

2.2.4 鐵芯的長細比計算

鐵芯的長細比

2.2.5 磁化場強度的確定

因為在長細比計算公式中已經考慮了圓筒形結構的因素，所以在圓筒形去磁系數計算公式中，可以用等效圓柱體去磁系數近似計算公式替代，其誤差將在允許范圍之內。其去磁系數近似計算公式有

則物理磁化率

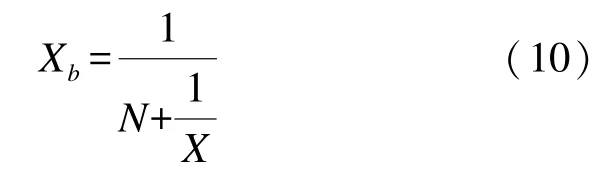
因此，鐵芯所需磁化強度為

按設計計算分析可知，兩端部磁場會逐漸減小，為保障工作區段磁場分布的均勻度，采用端部增加繞組匝數或增加端部鐵芯厚度的方法。鐵芯用一定厚度的冷軋電工鋼的薄板疊成，并通過2個壓環和8根符合要求的螺栓固緊。每個片層之間涂有絕緣粘合劑，使整個鐵芯固化為一個整體。鐵芯結構如圖3所示[3]。

圖3 鐵芯結構圖Fig.3 Structure diagram of iron core

為了保證鐵芯凹槽內正好繞下螺線管線圈所要求的匝數，必須按線徑大小經過嚴格的設計計算。在繞組間隙內填充密度符合要求的聚胺脂材料，可提供一定浮力。用同一鐵芯被2個正交磁場所磁化，其二繞組的設計計算方法按下述方法進行。

3 螺線管繞組的設計計算

首先分析螺線管繞組所產生的磁場與之對應的尺寸關系圖如圖4所示[4]。

圖4 有限長螺線管磁場與尺寸關系圖Fig.4 Relational graph between magnetic field and size of limited solenoid

按有限長通電螺線管軸上的磁場計算公式有：

式中：Hp是線圈軸線上某點P處的磁場；n是線圈單位長度上的匝數；I是線圈的通電電流；夾角β1和β2與線圈的尺寸關系如圖4所示。

如線圈長度為L，平均半徑為R，則中點處磁場為

根據圖3的三角函數關系有

將上述三角函數關系代入則有

4 馬鞍形繞組的設計計算

圖5 單匝馬鞍形線圈磁場與尺寸等效關系圖Fig.5 Equivalent relation diagram of magnetic field and size of single-turn saddle-shaped coil

馬鞍形線圈分上下二層，每層的幾何形狀和安匝數等參數都是一樣的，只是因為兩繞組合圍環抱鐵芯，其彎曲方向相反，但這不影響其產生磁場特征分析。按一層繞組中的一匝線圈，其所產生的磁場與之對應的尺寸關系等效圖如圖5所示。

把一匝馬鞍形線圈可看成是兩對邊相距為2C的平行直線，另外兩對邊是以0為中心，以R為半徑的兩段圓弧，只是圓弧段部分與直線段部分旋轉了90°。在求H0時，分別計算直線部分和圓弧部分，然后將二者按矢量和相加便是一匝線圈的模量值。

先按圖5一匝馬鞍形線圈磁場與尺寸等效關系圖，對單匝線圈通過函數積分運算求H0，然后再求二層整繞組的安匝數。單匝線圈通過函數積分運算如下。根據“分子電流”模型建立的觀點，有直線上dl段電流在0點處產生的磁感應強度的大小為

以β1為積分變數，因，又l＝ctanβ1，所以 dl＝csec2β1dβ1，又因為

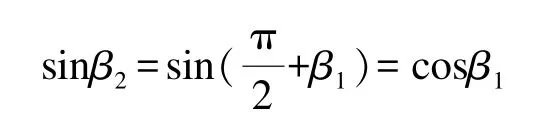
將上述關系式代入式(15)得

故兩直線段電流在0點處產生的磁感應強度的大小為

同樣，對每層單匝線圈兩圓弧段通過函數積分運算如下

所以得兩圓弧段電流在0點處產生的磁感應強度的大小為

同樣通過上述單位制關系的換算，即可得：

因為每層單匝馬鞍形線圈在0點處磁場應為

所以整個兩層馬鞍形線圈在0點處磁場應為

因為H＝C0H0＝0.86405C0IW，其中C0為調節系數，這與上下2個繞組之間的間隙大小有關，可選值在0.5～0.6之間，這里選0.5，根據H要求可得馬鞍形繞組總安匝數。

如選通電電流為I時，則馬鞍形繞組總安匝數為N2匝，為保證磁體磁場的對稱性和疊加效果，上下2個線圈繞組必須繞制方向一致，且串聯連接，設計每個線圈匝數為N1匝[5-8]。

5 結束語

采用同鐵芯、二繞組、同軸線、又正交的新方案設計了兩軸磁體用來模擬艦船磁場，相比于以往的單軸磁體，兩軸磁體提高了模擬艦船磁場的相似度。計算確定了鐵芯的材料、尺寸參數、繞組的通電電流及繞組的匝數。該兩軸磁體的設計方案既保證了兩軸磁體的體積和重量沒有超標，又使得磁體性能指標均達到或超過了預期目標。