基于數量化理論Ⅲ和極限學習機在小凈距隧道變形影響因素分析中的應用研究

趙淑敏

(陜西鐵路工程職業技術學院，陜西 渭南 714000)

0 引言

小凈距隧道受地形和線型的影響較小，且較連拱隧道具有更好的防水性能，使得其應用范圍越來越廣泛[1-2]。國內諸多學者開展了針對小凈距隧道的相關研究，并取得了相關的成果。如：李君君等[2-3]、宋章等[4]對小凈距隧道的變形機制及穩定性等進行了研究，雖取得了一定的成果，但多是偏重動荷載對隧道變形及穩定性的影響，缺乏針對隧道變形影響因素的綜合研究；婁霜[5]、于衛云等[6]、朱浩波等[7]通過對隧道變形影響因素進行綜合研究，為隧道施工方法及支護參數調整提供了依據，實現了隧道施工過程的動態設計，在保證施工安全的前提下，實現了工程造價優化。然而，上述研究對象均不是小凈距隧道。為準確分析小凈距隧道的變形影響因素，并考慮到分析對象的定性特征，為實現定量評價，提出利用數量化理論Ⅲ解決隧道變形問題；同時，也有將數量化理論Ⅲ應用于隧道工程的相關方面的研究，如沈中其等[8]、鄧皇根等[9]將數量化理論應用于隧道圍巖分級，為圍巖分級評定提供了一種新方法。另外，極限學習機是一種新的智能算法，具有參數設置簡單、泛化性好等優點，但該方法缺乏在小凈距隧道中的應用。

因此，本文提出利用數量化理論Ⅲ研究小凈距隧道的變形影響因素，并對各影響因素的影響程度進行評價判定，進而確定隧道變形的主要影響因素；其次，利用極限學習機構建小凈距隧道的變形預測模型，以驗證變形影響因素判斷準確性，以期為工程設計和施工提供參考依據，并驗證數量化理論Ⅲ和極限學習機在隧道工程應用中的有效性。

1 基本原理

1.1 數量化理論Ⅲ

數量化理論Ⅲ隸屬于多元統計分析，能有效實現定性變量對定量變量的影響程度分析，其基本思想為：基于若干分析樣本，以構造反應矩陣為基礎，通過矩陣變換，對相應影響變量及評價對象賦予相應得分，以判斷定性變量對定量變量的影響程度。鑒于文獻[10]已對數量化理論Ⅲ進行了介紹，該文不再贅述。

值得指出的是，為進一步評價定性變量對定量變量的影響程度，引入得分范圍R和方差比η來劃分各定性變量的影響程度，2個參數的計算公式為：

Rjk=maxbjk-minbjk；

(1)

(2)

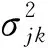
特征值個數與類目數相同，且特征值與得分向量b間具有一一對應的關系，使得樣品得分也有與之相對應的關系；同時，特征值越大，說明該特征值相對應的特征向量的可信度越高。由于最大特征值僅表示一維評價，因此，該文提出利用最大3個特征根進行組合，來分析定性變量對定量變量的影響程度。

1.2 極限學習機

極限學習機只需設置隱層神經元節點數即可，具有使用簡單、泛化能力強、可靠性高等優點[11-13]。若將分析樣本表示為(xi,ti)，i=1,2,…,n(n為分析樣本總數)，則極限學習機的激勵函數可表示為

(3)

式中：oj為網絡輸出向量；M為隱層節點數；βi為輸出權值向量；wi為輸入權值向量；bi為隱層神經元的偏置；g(x)為激勵函數。

極限學習機可以零誤差逼近訓練樣本，即：

(4)

因此，存在wi、βi和bi，得：

(5)

式(5)可進一步轉化為矩陣形式，即：

Y=Hβ。

(6)

式中H為輸出矩陣。

由于H矩陣為常數矩陣，因此，極限學習機的學習訓練過程可表示為式(6)最小二乘解β′的求解過程，其計算公式為

β=H+Y。

(7)

式中：H+為H矩陣的廣義矩陣(摩爾-彭羅斯)。

2 實例分析

2.1 工程概況

小凈距隧道已被廣泛應用，由于小凈距隧道的雙洞間距較小，使得施工過程中的變形控制格外重要，有必要對其變形影響因素進行系統分析，以便指導現場工程施工，保證施工安全。該項目主要研究小凈距隧道的變形影響因素，數據來源于寧績高速十里巖小凈距隧道，隧道全線為Ⅴ級圍巖。隧址區位于丘陵構造剝蝕區，具低丘溝谷微地貌特征，區內最低高程為181.58 m，最高高程為302.0 m，高差120.42 m。隧道進口仰坡較陡，坡度大于50°，洞身地形起伏較小。

隧址區地表土層以第四系殘坡積層為主，呈灰黃色，中密—密實，土質不均，含60%碎石，粒徑2～4 cm，磨圓度較差，成分以泥灰巖為主；下覆基巖以泥灰巖為主，青灰色，較軟，具泥質結構、層狀構造，工程性質一般。區內地表水較發育，主要沿環繞隧道所在山體的溝谷流過，水質較好；地下水以裂隙水為主，受大氣降雨影響較大，且由于區內節理多為閉合狀，使得區內基巖的富水性較差。

在該隧道的實施過程中，對區內不同斷面的地質條件、施工條件及變形情況進行統計，共計21組樣本，監測數據包含了先行洞、后行洞的拱頂沉降和水平收斂，共計4組數據[14-15]。

2.2 變形影響因素分析

結合文獻[5-7]的研究成果及工程實踐經驗，隧道變形影響因素主要分為2個方面。一是隧道圍巖因素，即隧道周邊圍巖的固有性能參數；二是隧道施工因素，即施工過程涉及的參數，如支護參數等。因此，基于上述2個方面，確定隧道圍巖參數包括圍巖重度、變形模量、泊松比、抗剪強度、剪脹角及側壓力系數；而施工因素包括隧道埋深、噴射混凝土厚度、系統錨桿長度和隧道間距。同時，根據各參數的變形范圍，將其劃分為若干區間，劃分依據為以各影響因素的最大值和最小值為臨界值，將其近似等分為3個區間。通過劃分，得11個項目，32個類目，各項目、類目統計如表1所示。

表1 隧道變形影響項目、類目統計Table 1 Influencing factors for tunnel deformation

2.3 影響程度分析

基于數量化理論Ⅲ的分析原理，以matlab軟件實現該方法的理論計算，得到3個最大特征值分別為λ1=0.212 3，λ2=0.116 4，λ3=0.087 7，各特征值對應的特征向量如表2所示。各特征值對應的特征向量即為相應類目的得分。

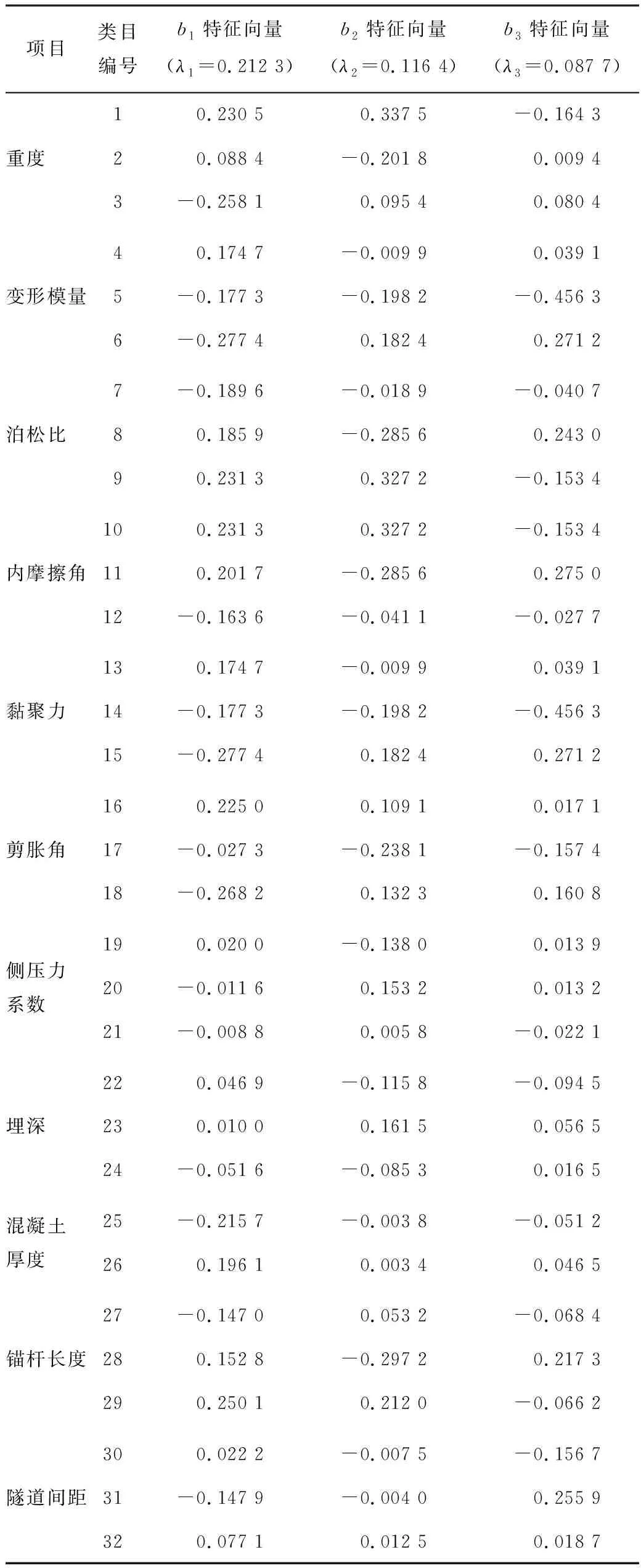
表2 各類目得分Table 2 Scores for every influencing factor

2.3.1 類目影響程度篩選

由于上述3個特征向量均能不同程度地代表各類目得分，為實現各類目得分的綜合分析，將3個特征向量分別投影到3個坐標軸上，并以其距離原點的距離(l)為評價指標，對各類目的影響程度進行篩選分類，共劃分為3類。其中，A代表主控因素(l>0.3)、B代表重要因素(0.2≤l≤0.3)、C代表一般因素(l<0.2)，結果如表3所示。

由表3可知: A類主控因素的類目編號為1、5、6、8、9、10、11、14、15、18、28、29，占類目總數的37.5%；B類重要因素的類目編號為2、3、16、17、25、26、31，占類目總數的21.9%；其余為C類一般因素，占類目總數的40.6%。同時，對比隧道圍巖因素和施工因素可知，圍巖因素中所占的A類控制因素相對較多，而施工因素中的B類控制因素相對較多，說明隧道圍巖條件對隧道變形起較強的決定作用，但通過對施工因素的控制，可以很大程度上控制隧道變形，這與實際工程相符。

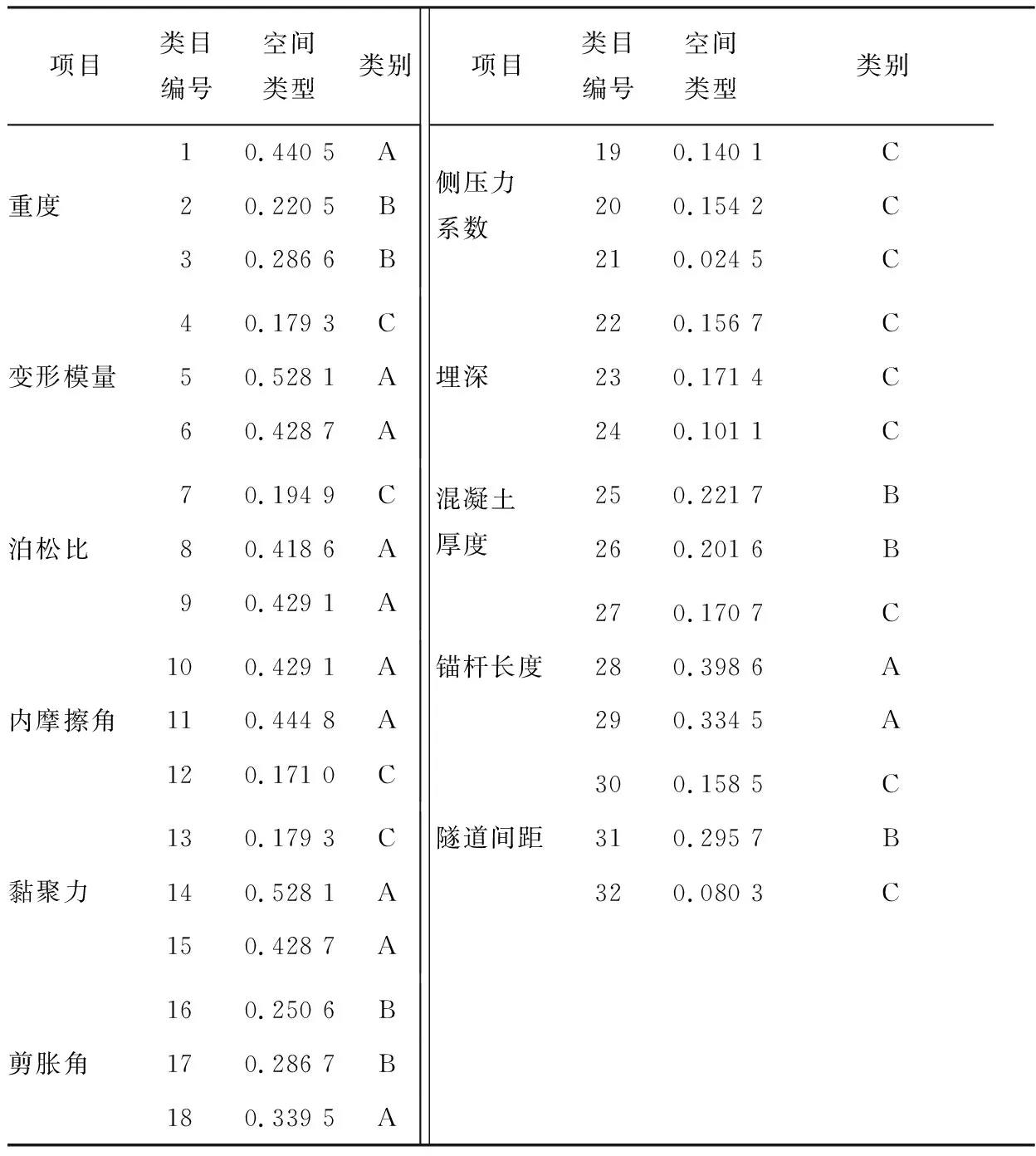
表3 各類目影響程度篩選統計Table 3 Screening results for influencing degree of every influencing factor

2.3.2 項目影響程度篩選

結合數量化理論Ⅲ的基本原理，再以得分范圍R和方差比η為評價指標，對各項目的影響程度進行篩選，且將各項目的影響程度也劃分為3類，即主導因素(R>0.45,且η>0.05)、重要因素(0.15≤R≤0.45,且0.008≤η≤0.05)和一般因素(R<0.15,且η<0.008)。同時，鑒于前述3個特征向量均能不同程度地代表類目得分，且當特征值越大，其分析所得參數的可信度越高。因此，為充分分析3個特征向量所蘊含的信息，該文以特征值為歸一化對象，進行歸一化處理，確定3者的組合權值，即[w1w2w3]=[0.509 8 0.279 5 0.210 6]。根據統計組合，得各項目的篩選統計如表4所示。

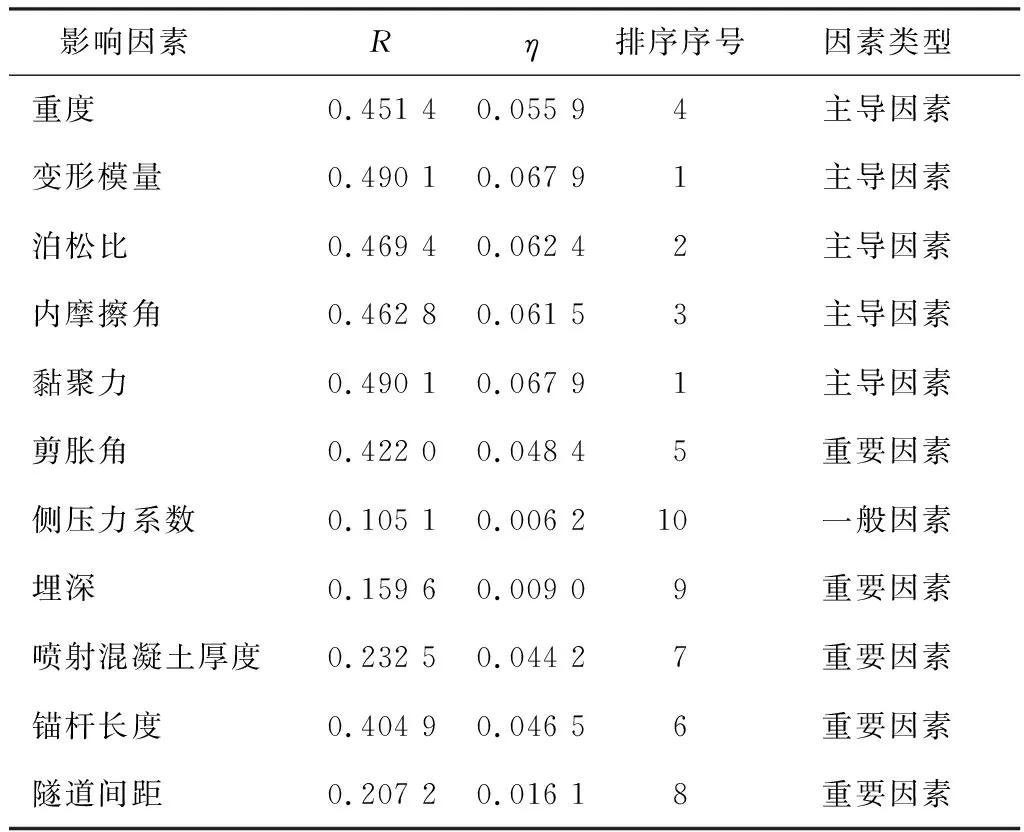
表4 各項目影響程度篩選統計Table 4 Screening results for influencing degree of every influencing factor

由表4可知：隧道變形的主導因素有圍巖重度、變形模量、泊松比、內摩擦角和黏聚力；重要因素有圍巖剪脹角、隧道埋深、噴射混凝土厚度、錨桿長度及隧道間距；而圍巖側壓力系數為一般因素。同時，據各項目的影響程度篩選結果可知，主導因素均為隧道圍巖因素，而施工因素全為重要因素，這也與各類目的分析結果相符。

結合工程實際應用，各影響因素在工程應用中應具有一定的限定條件或取值區間，因此，該文以表4中的分析結果為參照，建議以B、C類影響程度的各類目取值區間作為實際工程中的參考取值。

2.4 耦合作用分析

根據各類目得分，可求解各樣品得分，且考慮到基于3個特征向量計算可得到3個相應的樣品得分向量，因此，也對3個得分向量進行組合分析，組合權值仍為0.509 8、0.279 5和0.210 6，綜合確定各樣品得分。同時，為探討隧道變形影響因素間的耦合程度，基于項目影響程度篩選，剔除一般影響因素，類比上述過程，再次求解樣品得分，通過對比包含和不包含一般因素條件下的樣品得分來判斷影響因素間的耦合程度。結合文獻[10]的研究成果，樣品得分(K)可判斷樣品的危險性程度，結合該項目統計結果，將樣本危險性程度劃分為3級，即危險性高(K>0.03)、危險性中等(0≤K≤0.03)和危險性低(K<0)；同時，以2次計算得到的樣品得分差值為評價指標，確定各樣本的耦合程度，且當樣品得分差值大于0.015時，認為耦合度高，反之，則認為耦合度低。計算結果統計如表5和圖1所示。

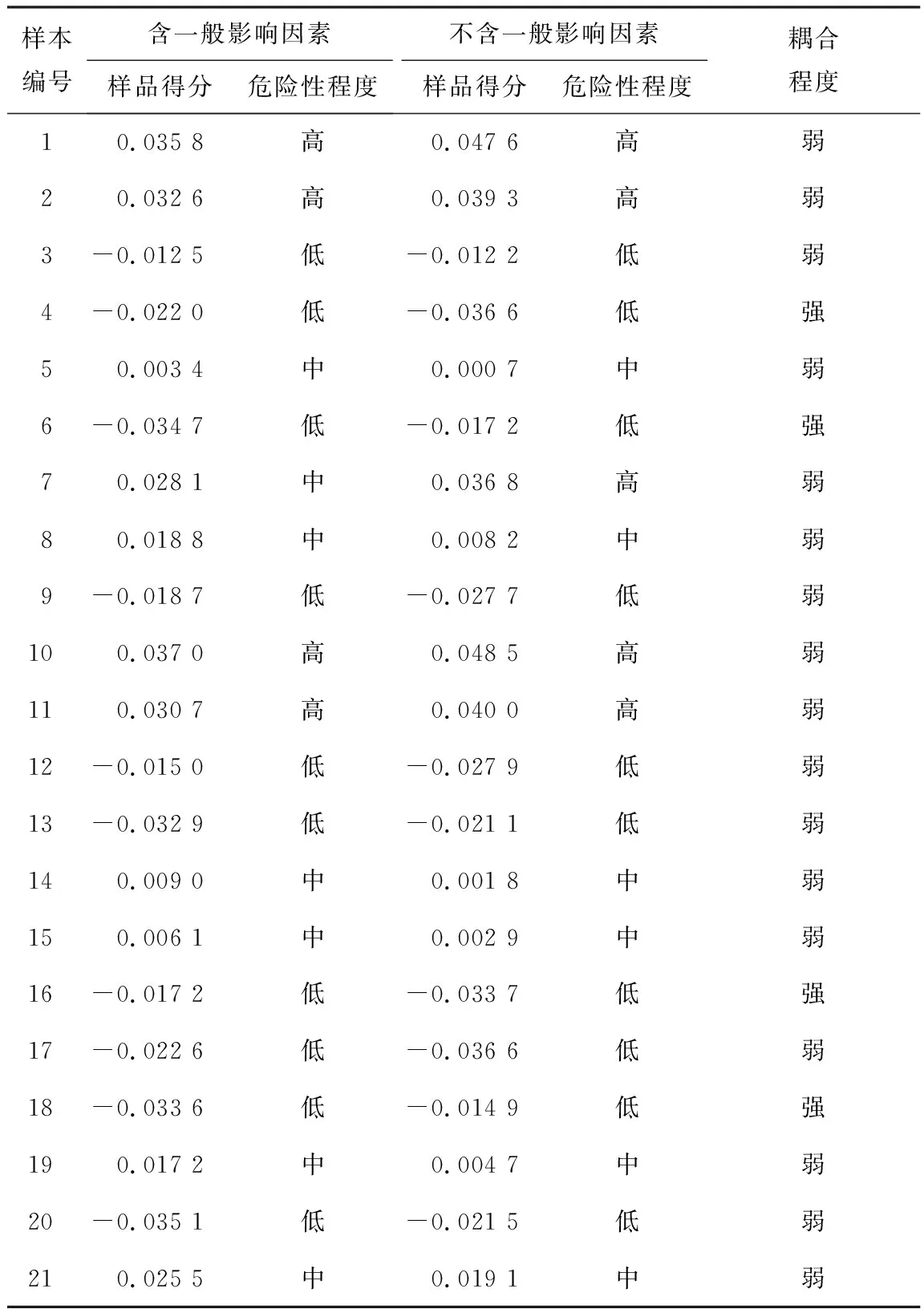
表5 影響因素間的危險性及耦合程度統計Table 5 Statistics on risk and coupling degree among different influencing factors

圖1樣品得分分布
Fig.1 distribution of sample points

由表5可知，通過去除一般影響因素，樣本得分存在一定的差異，說明一般影響因素對分析樣本的危險性判斷確實存在影響。其中：在含一般影響因素情況下，分析樣本危險性高所占的比例為19.05%、危險性中等所占的比例為33.33%、危險性低所占的比例為47.62%；在不含一般影響因素情況下，分析樣本危險性高所占的比例為23.81%、危險性中等所占的比例為28.57%、危險性低所占的比例為47.62%。同時，分析樣本4、6、16、18的耦合度高，占樣本總數的19.05%，其余樣本的耦合度均為低，說明一般影響因素對樣本得分的影響有限，也驗證了前文將影響因素劃分為一般影響因素的準確性。

2.5 可靠性驗證

為進一步驗證上述分析結果的可靠性，該文提出利用極限學習機構建隧道變形預測模型，輸入指標為隧道變形影響因素，輸出指標為對應的變形值；同時，為探討上述分析結果的準確性，該文先對先行洞的水平收斂進行預測，對剔除一般影響因素前后均進行預測，以驗證一般影響因素對預測結果的影響。另外，考慮到各樣本危險程度的差異，該文以危險性中等和低的15個樣本為訓練樣本，以危險性高的5個樣本為驗證樣本，預測結果如表6所示。

表6 先行洞水平收斂變形預測Table 6 Prediction of horizontal convergence deformation of advance tunnel

由表6可知: 剔除一般影響因素前后的預測結果具有差異，說明一般影響因素對預測結果具有明顯影響;在含一般影響因素情況下，預測結果的相對誤差均值為3.60%，而在不含一般影響因素情況下，預測結果的相對誤差均值為1.79%，后者預測精度明顯大于前者，說明一般影響因素會減弱變形影響因素與變形值間的關聯性，對變形規律分析不利，這與前文分析結果一致，驗證了隧道變形影響因素的影響程度劃分的準確性和可靠性。

同時，為驗證極限學習機在隧道變形預測中的適用性和可靠性，在剔除一般影響因素的情況下，再進一步對先行洞拱頂沉降、后行洞水平收斂和拱頂沉降進行預測，結果如表7所示。

由表7可知：先行洞拱頂變形預測結果的相對誤差均值為1.78%，后行洞水平收斂變形預測結果的相對誤差均值為1.95%，而后行洞拱頂變形預測結果的相對誤差均值為1.73%，得出極限學習機對先行洞和后行洞的變形預測效果均較好，驗證了該方法在隧道變形預測中的適用性和可靠性。

表7 隧道變形預測結果統計Table 7 Prediction results of tunnel deformation

同時，結合該文模型的實例驗證情況，將本文模型在工程實例中的應用機制分析如下：

1) 根據隧道工程實際，可初步分析相應的變形影響因素，再利用數量化理論Ⅲ分析各影響因素對隧道變形的影響程度；同時，基于分析結果，針對主導因素，采取針對性的控制措施，以保證隧道施工過程的安全。

2) 通過本文變形預測模型，可有效預測隧道的變形趨勢及變形量，可根據變形預測結果選擇合適的支護時機，以便更好地指導現場施工。

3 結論與討論

1)通過對小凈距隧道變形影響因素的數量化分析，得出隧道變形的主導因素有圍巖重度、變形模量、泊松比、內摩擦角和黏聚力，重要因素有圍巖剪脹角、隧道埋深、噴射混凝土厚度、錨桿長度及隧道間距，而圍巖側壓力系數為一般因素。

2)根據樣本得分計算，可有效判斷樣本的危險性程度；同時，隧道變形的一般影響因素會對樣品得分造成一定影響，即隧道變形影響因素間存在耦合性，且以分析樣本4、6、16、18的耦合度高，占樣本總數的19.05%，其余樣本的耦合度均為低。

3)通過構建隧道變形預測模型，進一步驗證了變形影響因素分析結果的準確性，也驗證了極限學習機在隧道變形預測中的適用性和可靠性。

4)該文僅分析了單一實例的變形影響因素，雖驗證了數量化理論在隧道變形影響因素分析中的適用性，但鑒于不同區域的工程實例具有不同的影響特征，因此，建議在該方法的應用過程中，應針對具體實例進行重新分析。