大瑞鐵路高黎貢山隧道原巖溫度預測

尹 龍, 李宜軒, 王樹剛,*, 蔣 爽, 羅占夫, 王 卓

(1. 中鐵隧道局集團有限公司勘察設計研究院， 廣東 廣州 511458； 2. 大連理工大學, 遼寧 大連 116024；3. 大連民族大學， 遼寧 大連 116600)

0 引言

隨著交通運輸的迅速發展及隧道施工技術的不斷提升，鐵路、公路等隧道建設規模越來越大。由于長隧道可以克服地形障礙，近年來深埋長隧道的數量得到快速增長。相比以往的鐵路、公路隧道，深埋隧道的熱害問題突出，作業環境惡化，嚴重影響施工人員的工作效率，而且由于產生的附加溫度應力還可能引起襯砌開裂，破壞隧道的穩定性[1]，故需要根據地溫的分布特征來對隧道高溫地段采取必要的降溫措施。本文研究的隧道地溫場位于大瑞鐵路高黎貢山越嶺地段。大瑞鐵路位于云南省西部，起于大理市，終于瑞麗市，線路在穿越高黎貢山時，以隧道形式通過。

一般來說，隧道周圍的原巖溫度隨埋深的增加而升高，特別是隧道上方的原巖溫度。隧道原巖溫度場的預測可以采用數值模擬和解析方法，并應用現場監測結果修正有關參數。陳永萍等[2]針對秦嶺隧道可能存在的熱害問題，分析鉆孔實測溫度等相關資料，建立了秦嶺隧道巖溫預測經驗公式，并對秦嶺隧道巖溫進行預測。楊平平[3]根據吉沃希嘎隧道鉆孔的實測溫度，運用加權平均值對數據進行回歸公式計算，得到相應的地溫計算公式及高地溫區地溫梯度。文獻[2-3]的研究針對地域性強，沒有廣泛的適用性。

陳尚橋等[4]運用導熱方程建立數學模型，并依據地質及地溫實測資料，在已知少量地溫數據作為擬合點的條件下，運用有限元反演法對水電站引水隧洞溫度場進行較準確的數值模擬研究。邵珠山等[5]通過建立兩端簡支的二維穩態熱傳導方程和平衡方程，導出了圓形斷面隧道邊界和圍巖的溫度場、位移場及應力場的解析解，在假設圍巖溫度已知的情況下，分析了隧道開挖造成的圍巖溫度變化的影響范圍。實際上在1950年，F.Birch[6]基于地質演化歷史的幾種不同假設提出了對地形的修正方法，獲得了2種地溫梯度修正值，分別對應于2個假設： 一是現有地形保持不變； 二是地貌特征來源于百萬年以來古老地表面的抬升和侵蝕。由此獲得了山體地表下某一埋深處的原巖溫度數學表達式，主要用于地熱流的計算，但沒有在隧道原巖溫度計算中得到廣泛應用。1979年和1994年，P.Bodmer等[7]和L.Rybach等[8]將F.Birch[6]方法中三維地形對某一點原巖溫度的影響簡化為溫度修正值，代入一個由地表面溫度和局部地溫梯度計算原巖溫度的表達式，并編寫計算程序預測隧道地溫場，將其應用于Gotthard公路隧道中進行地溫場測算，在受地下水影響較弱的隧道施工地段，計算值同溫度實測值吻合較好;但是未分析溫度修正值的簡化表達式對預測結果的影響。

本文基于F.Birch[6]提出的地質演化歷史方法，應用相應的地溫場計算模型(將P.Bodmer等[7]和L.Rybach等[8]的溫度修正表達式復原為F.Birch[6]提出的原始表達式)，特別是引入“谷地地理信息系統”獲取較為準確的地形數據，對高黎貢山隧道進行原巖溫度預測，并對隧址區的溫度場進行簡單劃分。

1 數學模型的描述

假定山體初始地表面和隧道橫斷面如圖1所示。經過地質演化(定義時間為t)后，抬升高度為L。隧道所處位置位于初始地表面下的距離為D，經過抬升后距離不變。P5為計劃開挖隧道中某個位置點，其對應的地表點為P2。

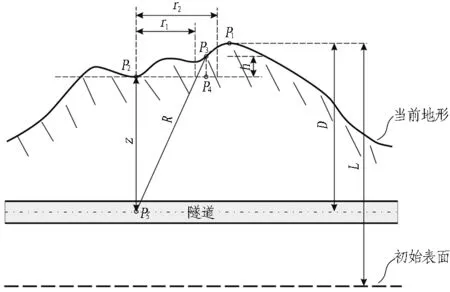
圖1 隧道橫斷面示意圖

一般情況下原巖溫度隨深度增加而升高，但是復雜的地形表面也會對地下埋深至數千米的巖溫產生影響。其他的影響因素還包括地表溫度、當地熱流密度及各種地質參數(如地質構造、熱導率、侵蝕率等)，其中地質參數影響導熱系數分布。在隧道未開挖條件下，基于固體熱傳導理論，在考慮地質演化歷史(包括抬升和侵蝕過程)的情況下，得到圖1中P5點溫度的簡化計算式，如式(1)所示[6]。

(1)

為簡化計算過程，以P2為圓心，將經過P2的平面劃分為若干個圓環，式中hr為每個圓環內地形的平均海拔高度與P2點海拔高度的差值。Er的計算如式(3)所示。

Er=E(β)=2erfc(β)-4i2erfc(β)。

(3)

其中：

ΔΩr/(2π)為圓環(內外半徑分別為r1和r2)與P5點的立體弧度，計算如式(6)所示。

重復上述過程，計算出隧道方向每間隔一定距離(如1 km)的原巖溫度。將計算結果與實測數據進行對比，可對α的取值進行修正。

對上述計算模型編制計算程序，根據每個采樣點的坐標位置更新所劃分圓環的數據，計算地形修正值，進而獲得預測的溫度值。

2 隧道山體概況和地形數據獲取

2.1 隧道山體概況

高黎貢山隧道位于怒江車站與龍陵車站之間，隧道進口里程為D1K192+302，出口里程為D1K226+840，隧道全長34 538 m。研究區域屬熱帶—亞熱帶季風氣候區，日照豐富，雨量充沛，氣溫年差小，日差大，年平均氣溫為14.9～19.5 ℃。受孟加拉灣暖溫氣流控制，研究區每年5—10月為雨季，11月—次年4月為旱季，年平均降雨量為967.1～2 105.7 mm，最大可達 2 597.7 mm。受地形條件的影響，降雨量有隨地形增高而增加的規律。

2.2 地形數據獲取

基于“谷地地理信息系統”，獲取計算點周圍約35 km的地形數據，對施工圖中地形數據進行擴充。將所獲取的地形數據與施工圖中若干位置的海拔高度進行對比，誤差在可接受的范圍之內。北京54坐標系下計算區域地形如圖2所示。

圖2 北京54坐標系下計算區域地形

Fig. 2 Calculation of regional topography in Beijing 54 coordinate system

2.3 計算參數取值

式(1)計算用到的幾個參數中，D近似取隧道在整個山體中的最大埋深，即1 200 m；L為山體抬升高度，近似取2 000 m；地表面溫度梯度α′根據實測數據擬合得到，為0.005 ℃/m；溫度擴散系數k，根據巖性參數近似取為0.02×10-4m2/s，經過敏感性分析發現k取值對計算結果影響較小；初始巖溫梯度α對結果影響較大，其取值根據實測數據，經過反算獲取，針對該隧道項目取值為0.013 5 ℃/m。此外，在地形修正值的計算中，距離計算點地面水平距離越近的地形對計算點溫度影響越大，故距離越近的圓環劃分越細，本文計算時，對于第i個圓環的內外半徑分別取為30×1.5i-1m和30×1.5im。

3 溫度預測

3.1 鉆孔溫度計算

將北京54坐標系下的鉆孔點平面坐標和相應埋深輸入計算程序中，計算相應的溫度，與實測溫度數據進行對比，從而對模型進行驗證。實測地溫數據選取文獻[9]中公布的若干鉆孔溫度數據以及項目施工圖中的地質勘測數據。北京54坐標系下計算區域鉆孔點坐標如表1所示。鉆孔溫度計算值與實測值對比分別如表2和圖3所示。從溫度值對比來看： 1)大部分計算值與實測值的變化趨勢一致，表明所建立的數學模型和計算程序是可靠的；2)個別鉆孔的計算值與實測值誤差較大，主要受地下水流的影響。當鉆孔內有以下滲為主的地下水垂向運動時，鉆孔內原始地溫將受地下滲水流的影響而降低；當鉆孔位置有地下熱水向上排泄的通道時，鉆孔位置附近原始地溫將會升高。程序計算時，參數取統一的數值，尤其是初始巖溫梯度α對結果影響較大，但并未針對局部特殊的地質特征進行修正。在隧道建設過程中，當發現實際地溫與預測值偏差較大時，應特別注意地下斷層及水流情況[10-11]。

3.2 隧道溫度計算

將從“谷地地理信息系統”中獲取的地形數據及相應的關鍵參數作為數據基礎。將隧道進口里程D1K192+302處取為計算起點，沿隧道約770 m取為第2點，此后以1 km為采樣間距，沿隧道取33個采樣點，第35采樣點距第36采樣點(計算終點)約768 m。將采樣點在北京54坐標系下的平面坐標及相應埋深輸入計算程序中，計算得到沿隧道方向未開挖情況下的地溫數據(不考慮斷裂帶的影響)。沿隧道方向巖石溫度曲線如圖4所示。可以看出： 1)在距隧道起點約8 770 m處，隧道原巖溫度達到最高，約 31.7 ℃； 2)沿隧道向瑞麗方向，巖溫呈現出先增大后減小的規律。

表1 北京54坐標系下計算區域鉆孔點坐標

表2鉆孔計算溫度與實測溫度對比

Table 2 Comparison between calculated temperature and measured temperature of boreholes℃

圖3 鉆孔溫度計算值與實測值對比

Fig. 3 Comparison between calculated temperature and measured temperature of boreholes

圖4 隧道巖溫預測

3.3 山體溫度計算

依據文獻[12]中介紹的高地溫分級和規范[13]：“隧道內氣溫不得高于28 ℃”，當氣溫超過28 ℃時，高地溫引起的熱害問題開始嚴重，需要采取降溫措施。山體溫度場分布如圖5所示。可沿隧道洞線方向進行溫度劃分： 沿隧道瑞麗方向，隧道開始大約2.5 km以內及18 km至隧道終點段，隧道巖溫為28 ℃以下；2.5～18 km段隧道巖溫為28～31.73 ℃，需要進行實時溫度監控，采取必要的降溫措施，例如加強隧道內通風、采用冰制冷系統及建立制冷站作冷源等[14-15]。綜上可知，需根據隧道所處環境及施工條件選擇最有效的解決方案。

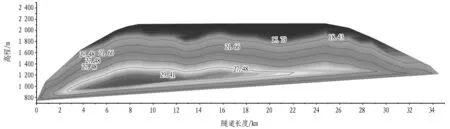
圖5 山體溫度場分布圖(單位： ℃)

深埋隧道的水文地質環境相對復雜，存在很多不可控因素，如山體內的溫泉水流和地表的補給水流都將影響著隧道上方山體的溫度場；但在純導熱模式下計算的隧道原巖溫度趨勢與同時存在熱傳導-對流條件下的鉆孔實測溫度總趨勢基本一致。

4 討論與結論

1)基于地質演化歷史的方法，結合“谷地地理信息系統”獲取的地形數據，首先應用地溫場計算模型計算鉆孔位置的溫度，并將計算值與部分實測鉆孔溫度進行對比分析，修正當地地表溫度梯度、初始狀態下的巖石溫度梯度及溫度擴散系數等參數。經驗證，基于地質演化歷史方法的原巖溫度預測模型符合計算需求。

2)依據原巖溫度預測模型編制相應的計算程序，在純導熱模式下計算隧道原巖溫度。沿隧道向瑞麗方向，隧道原巖溫度有先增大后減小的趨勢，最高點溫度為31.73 ℃。

3)根據隧道山體的預測溫度，沿洞線方向進行溫度區域劃分，隧道開始大約2.5 km以內及18 km至隧道終點段，隧道巖溫為28 ℃以下；2.5～18 km段隧道巖溫為28～31.73 ℃。三維坐標系下的原巖溫度預測模型及隧道山體原巖溫度計算需進一步研究和改進。

4)原巖溫度預測模型是在純導熱模式下建立的，計算鉆孔溫度時，部分鉆孔的計算值與實測值誤差較大，其誤差主要是由于鉆孔受到地下斷裂和地下水流影響引起的。考慮斷裂和地下水的存在，對流-導熱的原巖溫度預測模型需進一步研究。