基于小波分析的灰色SVM在變形預測中的應用

陸杰，覃書林，徐寧輝

(南寧勘察測繪地理信息院，廣西 南寧 530001)

1 引 言

隨著國家經濟快速發展，變形預測已成為工程和自然災害防災減災最直接、最重要的方法之一。定期對變形體進行監測，收集變形數據，分析變形規律，建立更為準確的變形預測模型，對保證人民生命財產安全具有重要的意義。針對這一問題，國內外許多學者已提出了多種方法，如時間序列模型、灰色模型、神經網絡、支持向量機以及各種組合方法等[1～3]。然而，受多種因素共同作用的結果，滑坡或建筑物往往呈現出較強的非線性和隨機性，給模型預測帶來了難度，且每一種方法都存在自身的局限性，沒有一種方法能夠完全適應各種情況下的預測和分析。支持向量機[4](Support Vector Machines，SVM)作為一種新的人工智能學習方法，在解決小樣本、非線性及高維模式識別等領域具有許多特有的優勢，已在變形預測中得到廣泛應用。因此，針對各單一預測模型存在的缺陷，許多學者展開了多模型融合預測的研究，取得了較好的結果[5～8]。然而，組合模型的思路往往局限于從原始變形序列本身探討變形預測問題，通過對預測殘差修正或各預測值組合加權方法實現變形的預測。這樣的組合思路并沒有從變形體自身的變形特點出發，忽略了變形體隱含的特征信息，不利于預測模型的推廣和預測精度的提高。

基于上述研究，本文從時頻挖掘出發，提出基于小波分析的灰色支持向量機變形預測新算法。算法主要研究如何從復雜的原始變形序列中提取出不同頻率的特征信息，并針對各分量的特點，建立更為合適的灰色支持向量機預測模型。同時，考慮到SVM模型的參數優化問題，采用網格搜索法[9]進行尋優，該方法用于小樣本數據預測時比遺傳算法、混沌優化算法較有優勢。經兩個算例，并與灰色模型、BP神經網絡和支持向量機對比分析，驗證新算法的可行性和有效性。

2 基于小波分析的灰色支持向量機預測模型

2.1 小波分析

小波分析是現代分析方法中的一種強有力的工具，小波分析的核心內容為小波變換，傅里葉變換是小波變換的數學基礎。小波變換的概念是在1983年由法國地球物理學家J.Morlet在分析處理地球物理勘探資料時提出來的，具有多尺度分析的功能。由于變形序列是通過實際觀測得到的離散數據，用小波變換進行預處理，可以有效提取數據的特征信息。本文采用Daubechies小波對變形監測數據序列進行分解。其原理參考文獻[10]。

2.2 灰色支持向量機預測模型

(1)灰色模型

灰色系統分析方法建模可以做到所需序列信息少，不用知道原始數據分布的先驗特征，可以通過有限次的生成便可將雜亂無規律的序列轉化為有規則、規律性較強的序列，建立生成序列和時間的關系函數模型。其方法和原理參考文獻[11]。

(2)SVM模型

其模型如下[4，9]：

設一組樣本訓練集為{(xi，yi)|i=1，2，…，l|}，其中xi∈Rn，yi∈R，xi為n維輸入向量，yi為輸出向量。將樣本通過非線性映射函數運算，從原空間映射到高位特征空間上，在高維特征空間中構造最優決策函數。

f(x)=WTφ(x)+b

(1)

式中，f(x)為估計函數，WT為權值向量，W∈Rn；φ(x)為核函數，φ(x)∈Rn；b偏置量，b∈R。W、b為待定系數。

引入結構風險函數，在優化問題的實現過程中，估計函數會被不敏感損失函數轉化，而不敏感函數ε可以表示為：

(2)

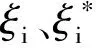
上述函數轉化的過程中，應滿足下面的約束條件：

(3)

為實現二次規劃求解，利用對偶理論對其進行轉化，則對偶式可表示為：

(4)

式中，拉格朗日乘子用a、a*表示；函數乘積用Q表示。

可將約束條件表示為：

Qij=K(xi，yj)=φ(xi)Tφ(xy)

(5)

式中，K(xi，yj)指的是支持向量機的核函數。

經過上述運算可將SVM的預測模型表示為：

(6)

由于SVM的性能很大程度上取決于核函數K(xi，yj)、核參數δ和正則化參數γ的選取。因此，選定能較好地反映模型復雜程度的徑向基核函數作為SVM的核函數，采用網格搜索法進行最優參數的選取。

2.3 模型預測流程

本文采用db6小波對變形序列進行分解。根據已有的文獻和資料，小波分解往往采用3層～5層較為適合。因此，本文將變形序列分解為4層，得到低頻余量a3和高中頻分量d1、d2、d3。設監測序列有n期，選取各分量和余量的前m期序列建立訓練樣本，后(n-m)期作為預測結果測試。由于d1、d2和d3分量往往具有一定的非線性和隨機性，低頻余量a3體現出趨勢項的變化，因此，本文選取能夠較好解決非線性問題的支持向量機模型和對線性問題具有較好預測能力的灰色模型進行預測，具體流程如圖1所示。

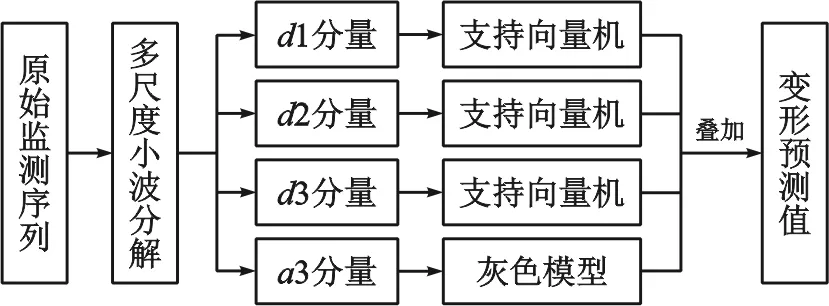
圖1 模型預測流程

3 算例分析

3.1 算例1

選取某滑坡9號監測點46期拉裂變形觀測數據進行分析[12]，其垂直位移變形如圖2所示。

圖2 滑坡垂直位移序列

由圖2可看出，滑坡位移變形總體呈現下降趨勢，隨機變化性較強，呈現非線性變化趨勢，變形的最小值為 2.3 mm，最大值為 24.8 mm。直接采用傳統的模型進行預測，不利于準確把握變形的規律。

因此，本文選取db6小波對原始序列進行4層分解，分解結果如圖3所示。

從圖3可看出，經小波分解得到的各分量能夠更好地反映原序列的局部特征和變化趨勢，具有較低的非線性和非平穩性特征。對比發現，d1、d2、d3分量明顯趨于平穩，且頻率依次降低，其中，d1預測分量表現了變形序列中的隨機性，而d2、d3預測分量則反映序列中一定的周期性。余量a3屬于低頻部分，代表了變形序列中隨時間變化的趨勢。可見，經小波分解后各分量變化曲線比原變形序列曲線更光滑、更平穩，有利于下一步的建模預測和分析工作開展。

圖3 小波分解結果

為驗證本文算法的可行性、有效性和優越性，建立4種方案進行分析比較：方案1—灰色GM(1，1)模型；方案2—BP神經網絡模型；方案3—支持向量機模型；方案4—本文算法。以前36期作為訓練樣本，后10期作為測試樣本。其中，方案1～3直接采用原始數據建模，方案4采用經小波分解重構后的各分量建模，即支持向量機模型對d系列分量進行訓練和預測，灰色模型對a3余量進行訓練和預測。為了加快SVM的收斂速度和降低建模誤差，將d系列分量歸一化到[-1，1]區間，經模型預測后再還原到原始區間。對于支持向量機模型的參數選取，利用網格搜索法對懲罰參數c和核參數g進行尋優，設置δ和γ的選擇范圍和參數步長分別為：δ∈[2-8，28]，γ∈[2-8，28]；粗選步長為1，精選步長為0.5。

4種方案的預測結果對比如表1所示，圖4反映了各模型的預測殘差結果。

各模型預測結果對比表 表1

圖4 各模型預測殘差對比

由表1和圖4可見：方案1對非線性變化的變形序列預測極不穩定，預測值呈線性變化，大部分預測值和實際值相差較大，最大、最小殘差值分別為 5.370 mm、0.180 mm。方案2的預測結果優于灰色模型，但容易出現極大和極小值，最大殘差值為 2.610 mm，最小殘差值則為 -0.010 mm，總體預測結果依然不穩定。而方案3和本文算法對原始序列的預測結果都比較好，相對來說本文算法預測結果最好，殘差曲線變化較為平緩，殘差最大值為 0.292 mm，最小殘差值僅為 0.004 mm。

3.2 算例2

為了進一步驗證本文算法對突發變形預測的性能，以某大壩的0+119壩段具有代表性的DC01監測點垂直位移量[13]，如圖5示。該變形序列共21期，監測時間從1996年7月開始，一直持續到1997年1月，觀測頻率為每個月3次。

由圖5可以看出，大壩變形極其不穩定，具有較強的非線性變化趨勢，前10期總體表現出有一定周期性的下降態勢，后11期則總體表現出強隨機性的上升態勢，18期～21期更是持續急劇上升，且變形的最小值為 42.18 mm，最大值為 60.68 mm。可見該大壩變形隨機變化性較強，采用傳統的預測算法，很難得到較好的預測值數據。

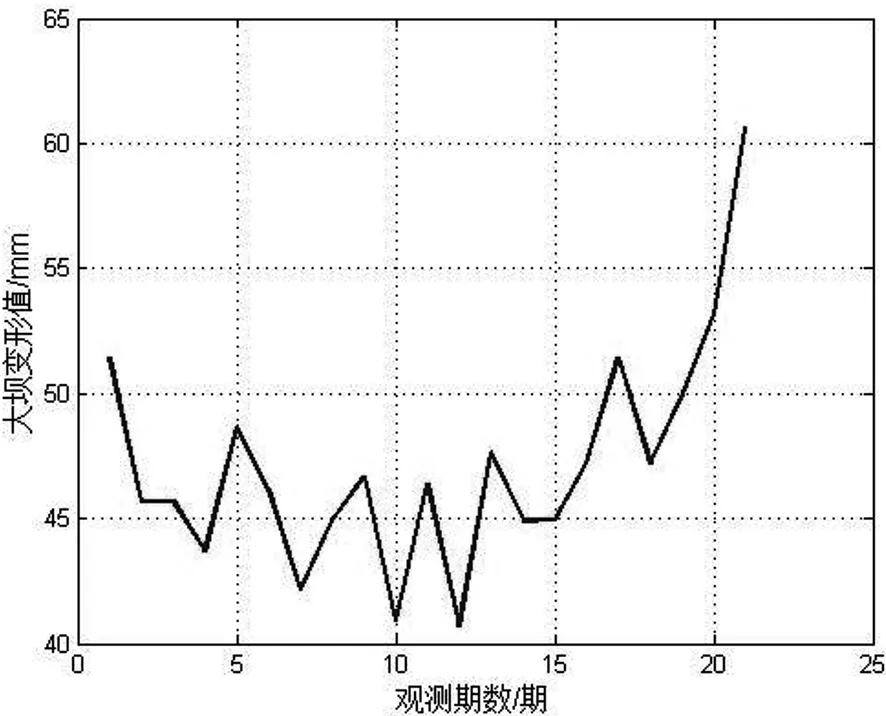
圖5 大壩變形垂直位移序列

同算例1，選取db6小波對大壩變形原始序列進行分解，分解結果如圖6所示。分別選取1期～16期數據作為訓練樣本，17期～21期數據作為測試樣本，建模方法和算例1一樣。各模型預測結果如表2所示，圖7給出了各模型的預測殘差曲線圖。

圖6 小波分解結果

各模型計算結果對比 表2

圖7 各模型預測殘差對比

由表2和圖7可見，灰色模型和BP神經網絡的預測結果極不穩定。在變形序列急劇變化的情況下，灰色模型的預測結果極不穩定，出現失真現象，特別是21期的預測結果已遠遠偏離監測值，無法找到變形規律；BP神經網絡模型在監測值急劇上升階段也出現了極大、極小值的情況；支持向量機模型的部分預測結果也不夠穩定，預測的誤差曲線呈線性遞增。而本文算法的預測殘差曲線較為平緩，殘差最大值僅為 -0.300 mm，最小值為 -0.013 mm，預測精度遠優于其他模型。

為了進一步綜合評定本文算法的性能，采用均方根誤差(RMSE)和平均絕對誤差(MAE)兩項精度指標進行評定，如表3所示。

各模型計算結果對比 表3

由表3可知，灰色模型的預測精度最低，其次是BP神經網絡模型，單一的支持向量機模型和本文模型的預測精度都表現出較好的預測精度，而本文算法的預測精度相較支持向量機有了進一步提高，均方根誤差分別為 0.184 mm和 0.165 mm，平均絕對誤差分別僅為 0.173 mm和 0.139 mm。可見，基于本文算法在一定程度上保證了較好的局部預測值和較優的全局預測精度。

4 結 論

本文將小波分析、灰色模型和支持向量機相結合引入到變形預測中，經理論和算例表明：①采用小波原理能有效分離出變形中隱含的非線性、隨機性和趨向性特征信息，優化了原始信號，更好地反映變形的局部特征和變化趨勢。②采用支持向量機和灰色原理相結合建立各分量預測模型，在一定程度上避免了灰色模型存在的理論缺陷，充分發揮了人工智能的優勢，進一步提高了預測精度。考慮到僅從單一的變形序列本身建立多尺度預測模型，對于各種環境條件下的變形預測問題需要進一步的驗證，如何將各特征信息與各影響因素相結合建立多尺度預測模型將是下一步研究的內容。