兩種縱骨端部連接形式的疲勞強度分析

(南通中遠川崎船舶工程有限公司，江蘇 南通 226005)

H-CSR[1]制定和實施直接關系到船舶設計、建造，以及新船型開發等一系列重要問題[2]。《H-CSR規范》要求計算縱骨端部的疲勞強度，其中，確定縱骨端部連接形式的應力集中系數十分關鍵。IACS H-CSR TB Report[3]介紹了《H-CSR規范》中的應力集中系數是通過數值計算和結構試驗得來的，且該系數與腹板加強筋的深度、縱骨面板的厚度以及細化網格的尺寸等均有關系。

《H-CSR規范》對32種特定類型的縱骨端部連接形式的應力集中系數進行了統一，做成了應力集中系數表格。但如果設計的結構形式不在這32種當中，《H-CSR規范》提供了替代設計方法來計算這種結構形式的應力集中系數。

Type A和Type B為船舶結構設計中常用的兩種縱骨端部連接形式(見圖1)，不在《H-CSR規范》提供的32種縱骨端部連接形式中。但Type A和《H-CSR規范》縱骨端部連接形式應力集中系數表格中的Type 2比較相近，均屬于非軟趾、軟根結構形式；Type B和其中的Type 4比較相近，均屬于軟趾、軟根結構形式。

文中重點證明Type A和Type B的應力集中系數與Type 2和Type 4的應力集中系數相當，因此針對以上4種結構形式選取相同腹板加強筋尺寸、相同的縱骨尺寸、相同的細化網格尺寸以及相同的載荷和邊界約束等條件進行研究，對比分析其應力集中系數差異。

介紹縱骨端部連接形式的應力集中系數替代設計方法的計算過程，說明名義應力和熱點應力計算的理論基礎，計算Type A & Type B與Type 2 & Type 4應力集中系數的差異，并基于該應力集中系數，以某型船舶為例，分析該應力集中系數對某縱骨疲勞壽命的影響，以及對腹板加強筋屈服強度的影響，證明使用Type 2 & Type 4替代Type A & Type B形式計算縱骨疲勞強度是可行的。

1 縱骨端部連接形式的應力集中系數替代設計方法

由《H-CSR規范》第9章可知，承受軸向載荷時的縱骨端部連接形式的應力集中系數Ka，和承受彎曲載荷時的應力集中系數Kb，可按下式計算：

(1)

式中：σHSAx為計算點承受軸向載荷時的熱點應力；σNomAx為計算點承受軸向載荷時的名義應力；σHSBd為計算點承受彎曲載荷時的熱點應力；σNomBd為計算點承受彎曲載荷時的名義應力；Kn為非對稱型材的應力集中系數，對于T型材Kn=1

1.1 有限元模型范圍及網格尺寸

在縱骨方向上取4個強框架間距，所考慮節點位于中間框架；在寬度方向，兩邊各取半個縱骨間距；垂向方向，取腹板高度的一半。

網格尺寸與縱骨面板厚度相同，其他部分網格尺寸取為縱骨間距的1/10，模型以mm為長度單位建模。

縱骨面板單元的x軸方向與縱骨方向相同，且法向需調成一致，便于插值計算熱點應力；外板單元法向需調成一致，便于加載。

1.2 軸向載荷工況

載荷工況為在模型后端部施加1 mm的縱向強迫位移，見圖2。

邊界條件為對稱邊界條件，見圖3。

1)帶板縱向邊緣：線位移δy=0，角位移θx=0。

2)強框架垂向邊緣：線位移δy=0，角位移θz=0。

3)強框架頂部：線位移δz=0，角位移θy=0。

4)腹板加強筋頂部：線位移δz=0，角位移θx=0。

5)模型前端剛固。

1.3 側向載荷工況

在縱骨帶板上施加均布單位載荷(0.001 MPa)，見圖4。

邊界條件為對稱邊界條件，見圖5。

1)帶板縱向邊緣：線位移δy=0，角位移θx=0。

2)強框架垂向邊緣：線位移δy=0，角位移θz=0。

3)橫框架頂部：線位移δz=0，角位移θy=0。

4)腹板加強筋頂部：線位移δz=0，角位移θx=0。

5)模型前端和后端剛固。

2 名義應力的計算

1)軸向載荷工況下，點A和點B的名義應力可按如下公式進行計算。

(2)

式中：Δl為軸向強迫位移，通常取單位長度，1 mm；L為有限元模型的總長度，mm；E為彈性模量，2.06×105，MPa。

2)側向載荷工況下，計算點A和計算點B的名義應力σNomBd可按如下公式進行計算[4]。

(3)

式中：s為縱骨間距，mm;l為縱骨總彎曲跨距，mm；P為側向壓力，通常取單位載荷1 kN/m2，即0.001 MPa；Zeff-n50為計入帶板扣除0.5tc腐蝕增量的剖面模數，mm3。xe為熱點位置到總跨距端部的最短距離，見圖6。

3 熱點應力的計算

通過對軸向載荷工況和側向載荷工況的有限元計算，可得到各單元的表面應力，熱點應力插值單元見圖7，熱點應力讀取位置Xshift如黑點所示，距趾端0.5tn50，其中tn50為縱骨面板凈厚度。

讀取縱骨面板上插值單元上表面的應力分量σxi，σyi，τxyi，其中i=1、2、3、4。對插值單元應力分量的線性內插[5]，得到σxj，σyj，τxyj，其中j=A,B。再通過線性內插或線性外插得到Xshift位置處的應力分量σx，σy，τxy，見圖8。

疲勞計算用熱點應力σHS可由Xshift位置處的應力分量σx，σy和τxy求得，理論基礎是材料力學中的一點的平面應力狀態理論。

如圖9所示，設Y軸為焊縫方向，也就是初始裂紋產生方向，X軸為焊縫的垂直方向，主應力1(σ1)作用于焊縫的垂直方向±45°范圍內，主應力2(σ2)作用于焊縫的垂直方向正負45°范圍外。

設主應力1與X軸成θ角，則由一點的平面應力狀態中主應力1和主應力2相互垂直可知，主應力2與X軸成θ+90°夾角。

(4)

(5)

為與《H-CSR規范》中對熱點應力計算方法的要求一致，進一步區分焊縫的垂直方向±45°范圍內和±45°范圍外的主應力，則±45°范圍內主應力為

(6)

±45°范圍外主應力為

σHS2=σ1+σ2-σHS1

(7)

所以，Xshift位置處的熱點應力為

σ=max(|σHS1|,|σHS2|)

(8)

根據《H-CSR規范》熱點應力計算方法，疲勞計算用熱點應力值為

σHS=1.12σ

(9)

4 結果分析

采用替代設計方法，基于相同腹板加強筋尺寸、相同的縱骨尺寸、相同的細化網格尺寸以及相同的載荷和邊界約束等條件，對Type A和Type B、以及Type 2和Type 4共4種結構形式的應力集中系數進行分析，將計算所得的縱骨端部連接形式的應力集中系數帶入某型船數據庫進行疲勞強度分析，分析其對疲勞壽命的影響，以及對腹板加強筋曲服強度的影響。

相關計算參數數值見表1。

表1 有限元模型尺寸 mm

1)通過有限元計算，Type A和Type 2的應力集中系數及其疲勞壽命見表2。

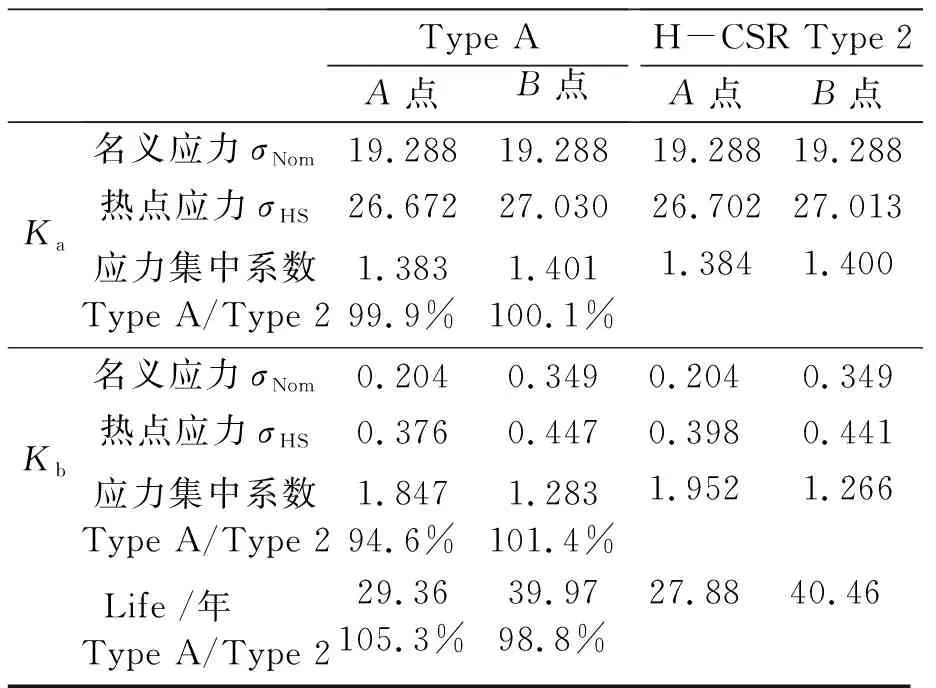
表2 Type A和Type 2的應力集中系數及其疲勞壽命

由表2可知：

(1)針對A點，Type A相對于Type 2應力集中系數略有減小，疲勞壽命略有增加。

(2)針對B點，Type A相對于Type 2應力集中系數略有增加，疲勞壽命略有減小。

(3)對于非軟趾、軟根形式的縱骨端部連接形式，疲勞強度通常由非軟趾(A點)處決定。

(4)總體來說Type A使非軟趾、軟根形式的縱骨端部連接形式的疲勞壽命略有增加。

2)通過表2了解到了Type A和Type 2軟根(B點)的形狀變化對縱骨疲勞強度的影響，對腹板加強筋屈服強度的影響可由以下兩組圖說明，見圖10、11。

由圖10～11可以看出：

(1)針對腹板加強筋趾端(A點)，Type A相對于Type 2的Mises應力略有減小。

(2)針對腹板加強筋根部(B點)，Type A相對于Type 2的Mises應力略有增加，由于腹板加強筋根部通常情況屈服強度余量較大，且過往沒有發生屈服破壞或疲勞破壞的實例，因此該影響可以忽略。

3)Type B和Type 4的應力集中系數及其疲勞壽命見表3。

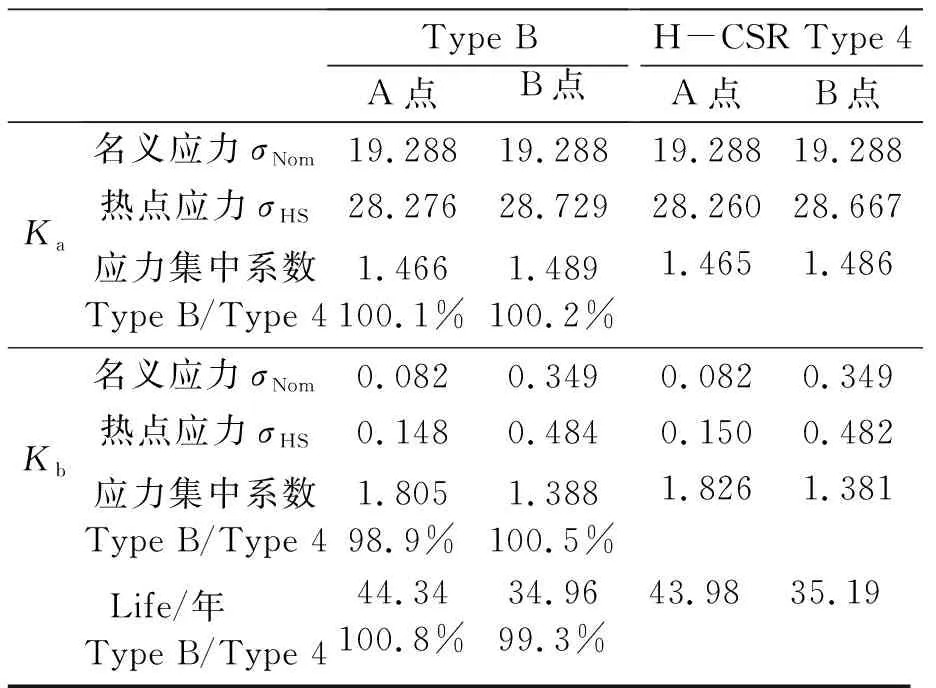
表3 Type B和Type 4的應力集中系數及其疲勞壽命

由表3可知：

(1)針對A點，Type B相對于Type 4應力集中系數略有減小，疲勞壽命略有增加。

(2)針對B點，Type B相對于Type 4應力集中系數略有增加，疲勞壽命略有減小。

(3)對于軟趾、軟根形式的縱骨端部連接形式，疲勞強度通常由軟根(B點)處決定。

(4)總體來說Type B使軟趾、軟根形式的縱骨端部連接形式的疲勞壽命略有減小，但減小幅度在1%以內。

4)通過表3了解到了Type B和Type 4軟根(B點)的形狀變化對縱骨疲勞強度的影響，對腹板加強筋屈服強度的影響可由圖12、13說明。

由圖12、13可見：

(1)針對腹板加強筋趾端(A點)，Type B相對于Type 4的Mises應力略有減小。

(2)針對腹板加強筋根部(B點)，Type B相對于Type 4的Mises應力略有增加，由于腹板加強筋根部通常情況屈服強度余量較大，且過往沒有發生屈服破壞或疲勞破壞的實例，因此該影響可以忽略。

5 結論

1)對于非軟趾、軟根形式的縱骨端部連接形式，疲勞強度通常由非軟趾(A點)處決定。

2)對于軟趾、軟根形式的縱骨端部連接形式，疲勞強度通常由軟根(B點)處決定。

3)Type A相對于Type 2的縱骨端部連接形式的疲勞壽命略有增加，且對腹板加強筋的屈服強度影響不大，因此在計算Type A形式的縱骨端部連接疲勞壽命時，使用Type 2的應力集中系數是可行的。

4)Type B相對于Type 4的縱骨端部連接形式的疲勞壽命略有減小，但減小幅度在1%以內，且對腹板加強筋的屈服強度影響不大，因此在計算Type B形式的縱骨端部連接疲勞壽命時，使用Type 4的應力集中系數是可行的。