幅度及多普勒信息輔助的多目標跟蹤算法

彭華甫，黃高明，田威，邱昊

1. 海軍工程大學 電子工程學院，武漢 430033 2. 中國人民解放軍92773部隊，溫州 325807

多目標跟蹤(Multi-Target Tracking, MTT)是未來信息化戰爭的關鍵技術之一，其目的是利用傳感器觀測數據估計目標數目及狀態[1]，在戰場監視、防空反導等領域應用廣泛。

經典的多目標跟蹤算法基于數據關聯的思想，將跟蹤過程分為數據關聯和狀態估計兩步。隨著目標及雜波數目的增加，數據關聯的復雜度呈指數增長。基于隨機有限集(Random Finite Set, RFS)[2]的多目標跟蹤技術，能有效避免復雜的數據關聯過程，成為目前多目標跟蹤領域的研究熱點。概率假設密度(Probability Hypothesis Density, PHD)濾波器是泊松分布下多目標后驗概率密度在Kullback-Lerbler準則下的最優近似[3]，證明了RFS算法的可行性，但算法穩定性差；勢概率假設密度(Cardinality Probability Hypothesis Density, CPHD)濾波器[4]在其基礎上引入目標數目的二階信息，以增大計算量為代價提高了跟蹤穩定性；由于PHD及CPHD采用序貫蒙特卡羅(Sequential Monte Carlo, SMC)實現時，狀態提取精度取決于聚類算法的穩定性，多目標多伯努利(Multi-target Multi-Bernoulli, MeMBer)濾波器[2]對多目標后驗概率密度函數進行數值近似，可直接估計目標數目及狀態，避免了復雜而不穩定的聚類過程。然而，當雜波數量增大時，這些濾波器跟蹤性能嚴重衰減。為提高雜波環境下的適應能力，利用幅度信息及多普勒信息可提高目標跟蹤性能[5-6]。文獻[7-9]分別將幅度信息引入到PHD、CPHD、MeMBer濾波器中，文獻[10-12]分別將目標多普勒信息引入到高斯混合PHD(Gaussian Mixture PHD, GM-PHD)、CPHD濾波器，均有效抑制了雜波影響。但由于PHD、CPHD、MeMBer濾波器理論的局限性，這些改進算法在高雜波環境下跟蹤性能受限，且無法直接形成航跡。

近年來提出的δ廣義標簽多伯努利(δ-Generalized Labeled Multi-Bernoulli,δ-GLMB)濾波器[13]，是多目標跟蹤的一種閉式解決方案，被證明是貝葉斯最優估計[14]，具有更強的雜波抑制能力、更高的估計精度且可直接估計目標航跡，在機動目標跟蹤[15]、衍生目標跟蹤[16]、多傳感器信息融合[17]等領域受到了廣泛關注。然而，其在實現中面臨計算復雜度大、強雜波和密集目標環境下“組合爆炸”的問題。對此，文獻[13]采用K最短路徑及排列分配算法進行假設裁剪，文獻[18] 結合量測分組大幅降低了計算量，文獻[19]結合吉布斯采樣裁剪及預測、更新合并提出了一種快速實現算法。

現有多目標跟蹤方面的研究大多僅利用目標的單一信息，隨著戰場環境的日趨復雜，綜合利用多種信息可從多個維度對算法進行優化，提高適應能力，是未來的一個發展趨勢。目前，基于δ-GLMB濾波器的研究還未考慮將幅度信息或多普勒信息引入其中以提高跟蹤性能，且現有算法雖進行了各種簡化處理，但強雜波環境下計算量仍較大。對此，本文通過聯合幅度及多普勒信息，基于δ-GLMB濾波器框架，提出了一種綜合利用多輔助信息的融合算法。通過引入幅度及多普勒信息對目標量測狀態進行擴展，利用幅度、多普勒及位置的聯合量測似然函數代替單一的位置量測似然函數，增強目標與雜波的區分度，推導了新的量測更新方程，提出了幅度及多普勒信息輔助的δ-GLMB濾波器(ADI-δ-GLMB)。仿真實驗表明，本文所提算法估計精度更高、抗干擾能力更強，且有效降低了高雜波環境下的計算量。

1 目標建模

1.1 狀態建模

假設二維運動場景中，k-1時刻有Nk-1個目標，其狀態可表示為

i=1,2,…,Nk-1

(1)

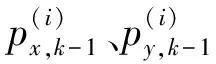
(2)

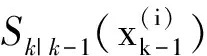
1.2 量測建模

引入幅度及多普勒量測信息后，k時刻目標量測可表示為

(3)

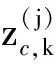
Zk=Θ(Xk)∪Kk

(4)

式中：Kk為虛警雜波量測集合；Θ(Xk)為檢測到的目標量測集合，檢測概率pD,k<1。

假設傳感器位于坐標原點，目標位置量測方程可表示為

zc,k=Hc,kxk+wk

(5)

式中：

其中：wk和Rc,k為位置量測噪聲矩陣和噪聲協方差矩陣。則目標位置量測似然函數為

g(zc,k|xk)=N(zc,k;Hc,kxk,Rc,k)

(6)

目標多普勒量測方程為

zd,k=hk(xk)+nk

(7)

式中：

其中：nk和Rd,k分別為多普勒量測噪聲和噪聲方差。

則目標多普勒量測似然函數為

g(zd,k|xk)=N(zd,k;hk(xk),Rd,k)

(8)

雷達系統中，回波信號幅度與回波平均信噪比(Signal-to-Noise Ratio，SNR)S有關，通常可將其建模為瑞利分布，目標幅度及雜波幅度的概率密度分別表示為[8]

(9)

(10)

假設檢測門限為τ，則經過門限檢測后，目標及雜波幅度的概率密度可表示為

(11)

(12)

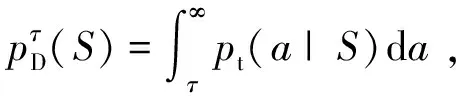
實際中，由于大氣、云層及目標雷達散射截面積(Radar-Cross Section，RCS)等因素的影響，目標回波SNR時變。假設回波SNR在[dB1,dB2]內均勻分布，對應S的取值范圍為[S1,S2]。則目標幅度似然函數可簡化表示為[8]

g(za|xk)=g(za)=

(13)

由式(5)和式(7)可以看出，目標位置量測、多普勒量測僅與目標狀態有關，回波幅度僅與回波信號SNR有關，可假設位置、多普勒及幅度量測間相互獨立。結合式(6)、式(8)和式(13)，位置、幅度及多普勒信息的聯合量測似然函數可表示為

g(zk|xk)=g{[zc,kzd,kza,k]|xk}=

g(zc,k|xk)g(zd,k|xk)g(za,k|xk)=

(14)

假設雜波量測的坐標、多普勒及幅度相互獨立，則聯合雜波密度可表示為

c(zk)=c(zc,k,zd,k,za,k)=

c(zc,k)c(zd,k)c(za,k)

(15)

式中：c(zc,k)為空間位置雜波密度函數；c(zd,k)為多普勒雜波密度函數；c(za,k)為雜波幅度似然函數[8]，其表達式為

(16)

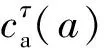
2 ADI-δ-GLMB濾波器

目標狀態可由標簽RFS表示為

X={(x,l)i}i=1,2,…,N

(17)

式中：x∈Xs為目標狀態向量；l∈Ls為其對應的標簽；X?Xs×Ls，Xs為目標狀態空間，Ls為離散的標簽空間。

假設k時刻，多目標后驗密度πk-1(X)服從δ-GLMB分布[13]

πk-1(X)=Δ(X)·

δI(L(X))(pk-1(·;ε))X]

(18)

式中：

I∈F(Lk-1)為標簽集合；Lk-1為k-1時刻的離散標簽集；F(L)為L的所有有限子集空間；L(X)為Xs×Ls→Ls的映射，有L((x,l))=l；ε∈Θ為歷史關聯；Θ為關聯空間；(I,ε)為關聯假設；ω(I,ε)為其相應權值；p(·;ε)為單目標概率分布；|·|為取勢計算；hX=∏x∈Xh(x)。

假設k時刻新生目標也服從δ-GLMB分布[13]：

πB,k(X)=Δ(X)·

(19)

式中：LB,k為新生目標標簽空間，Lk∩LB,k=?；pB,k(·)為新生目標概率分布。

2.1 預測

由于引入的幅度量測及多普勒量測信息并未影響目標的狀態轉移，因此，k時刻ADI-δ-GLMB濾波器的多目標預測分布πk|k-1(X)同標準的δ-GLMB濾波器，可表示為[13]

πk|k-1(X)=Δ(X)·

δI(L(X))(pk|k-1(·;ε))X]

(20)

式中：

2.2 更新

分析文獻[13]中標準δ-GLMB濾波器更新方程可以發現：引入幅度及多普勒量測信息對目標量測進行擴展后，僅對公式中的目標量測似然函數及雜波密度產生了影響。因此，分別用式(14) 和式(15)所示的聯合量測似然函數及聯合雜波密度代替原公式中的位置量測似然函數及雜波密度，則可得k時刻ADI-δ-GLMB濾波器的多目標更新分布

πk(X|Zk)=Δ(X)·

(pk(·;ε,ζk|Zk))X]

(21)

式中:

其中：Lk=Lk|k-1；pD,k(·)為目標探測概率；對于k時刻預測假設(I,ε)，ζk為目標與量測的關聯映射{l1,l2,…,l|I|}→{0,1,…,|Zk|}，當ζk(l)=0時，目標與空量測關聯，即目標漏檢；λ為雜波強度。

分析式(21)可以發現：當幅度信息無法獲取或利用幅度信息無法對目標與雜波進行區分時，gk(za,k|·)/c(za,k)=1，ADI-δ-GLMB濾波器僅受多普勒信息約束，退化為多普勒信息輔助的δ-GLMB(DI-δ-GLMB)濾波器；當多普勒信息無法獲取時，令gk(zd,k|·)/c(zd,k)=1，ADI-δ-GLMB濾波器退化為幅度信息輔助的δ-GLMB(AI-δ-GLMB)濾波器；當兩者都失效時，則退化為δ-GLMB濾波器。

2.3 計算復雜度分析

在算法實現時，為有效降低計算量，本文采用文獻[13]中的假設裁剪及文獻[18]中的量測分組技術來簡化計算。標準δ-GLMB濾波器僅利用位置量測信息，無法對真實目標與雜波進行區分，因此其更新步中的關聯過程需要考慮所有航跡假設，計算復雜度為O(NM3)，其中：N為目標個數，M為量測個數[16]。強雜波環境下，量測數據中包含大量雜波(M?N)，極限情況下量測分組失效，計算量成指數增長。而ADI-δ-GLMB濾波器綜合利用位置、幅度、多普勒信息，可從多個維度提高目標與雜波的區分度，從而可去除部分雜波量測的影響，理想條件下當利用輔助信息能將目標與雜波量測完全區分時，可使得M≈N，因此計算復雜度為O(N4)，大幅降低了計算量；當輔助信息失效時，計算復雜度為O(NM3)。

3 仿真實驗

假設有5個目標在二維觀測區域[-1 000,1 000] m ×[-1 000,1 000] m內作協同轉彎運動，目標運動狀態如表1所示，多普勒速度限定在[-35,35] m/s范圍內。

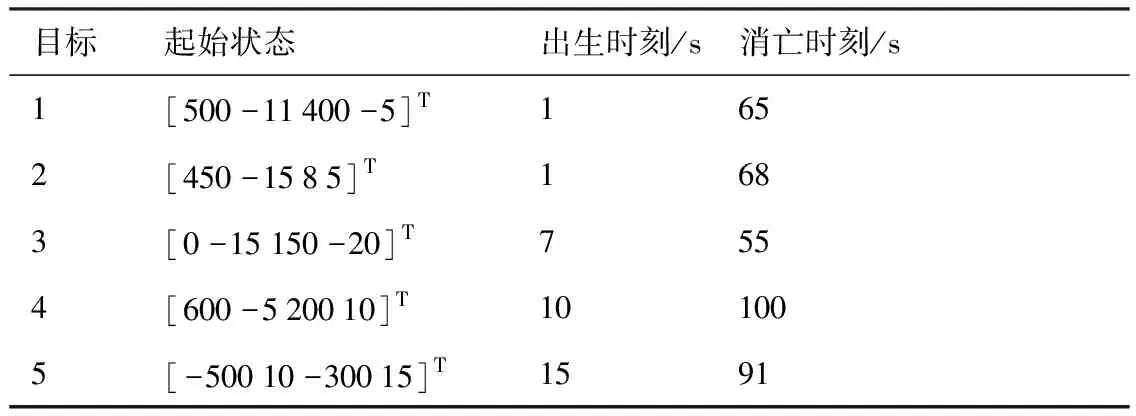
表1 目標運動狀態Table 1 Dynamic states of targets

目標狀態轉移矩陣為

過程噪聲協方差矩陣為

式中：σv=0.1 m/s為噪聲標準差；Ts=1 s為傳感器掃描間隔，掃描時間長度為100 s，目標存活概率pS=0.95。

圖1為ADI-δ-GLMB算法單次實驗結果，可以看出：強雜波下仍能對多目標進行有效跟蹤。

為評估算法的性能，對標準δ-GLMB[13]及信息輔助的幅度信息δ廣義標簽多伯努利(Amplitude Informationδ-GLMB, AI-δ-GLMB)[8]、多普勒信息δ廣義標簽多伯努利(Doppler Informationδ-GLMB, DI-δ-GLMB)[10]、ADI-δ-GLMB算法進行比較。分別進行100次蒙特卡羅實驗，并采用最優子模式分配(Optimal Sub-Pattern Assignment，OSPA)[20]作為評估因子，參數設置為：c=50、p=1。

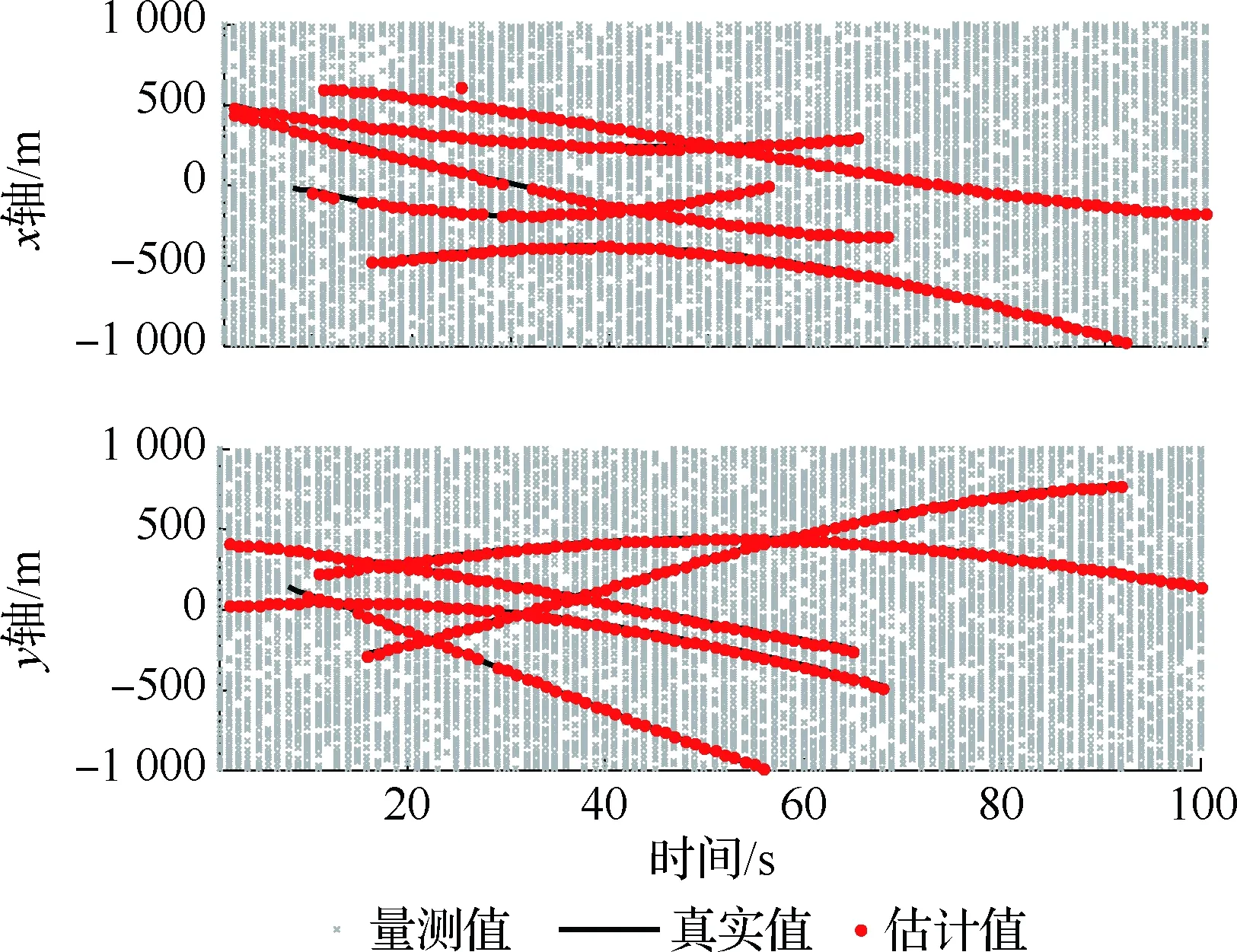
圖1 目標真實航跡和狀態估計Fig.1 True trajectories and state estimates of targets

圖2為不同算法的勢估計結果。可以看出：當雜波密集分布時，標準δ-GLMB會出現目標數目過估，且估計標準差較大；AI-δ-GLMB、DI-δ-GLMB、ADI-δ-GLMB濾波器能對目標數進行無偏估計，估計標準差更小。

圖3為不同算法的OSPA距離，可以看出：信息輔助的δ-GLMB相比標準δ-GLMB濾波器OSPA距離更小，且ADI-δ-GLMB濾波器OSPA距離最小，狀態估計精度最高。由于δ-GLMB類濾波器利用多幀量測信息計算假設概率，當目標消失時，之前的量測信息仍會影響當前時刻的概率分布，導致對目標消失反應慢，引起較大的估計偏差，因此當目標消失時這些濾波器的OSPA距離均會出現較大的尖峰。

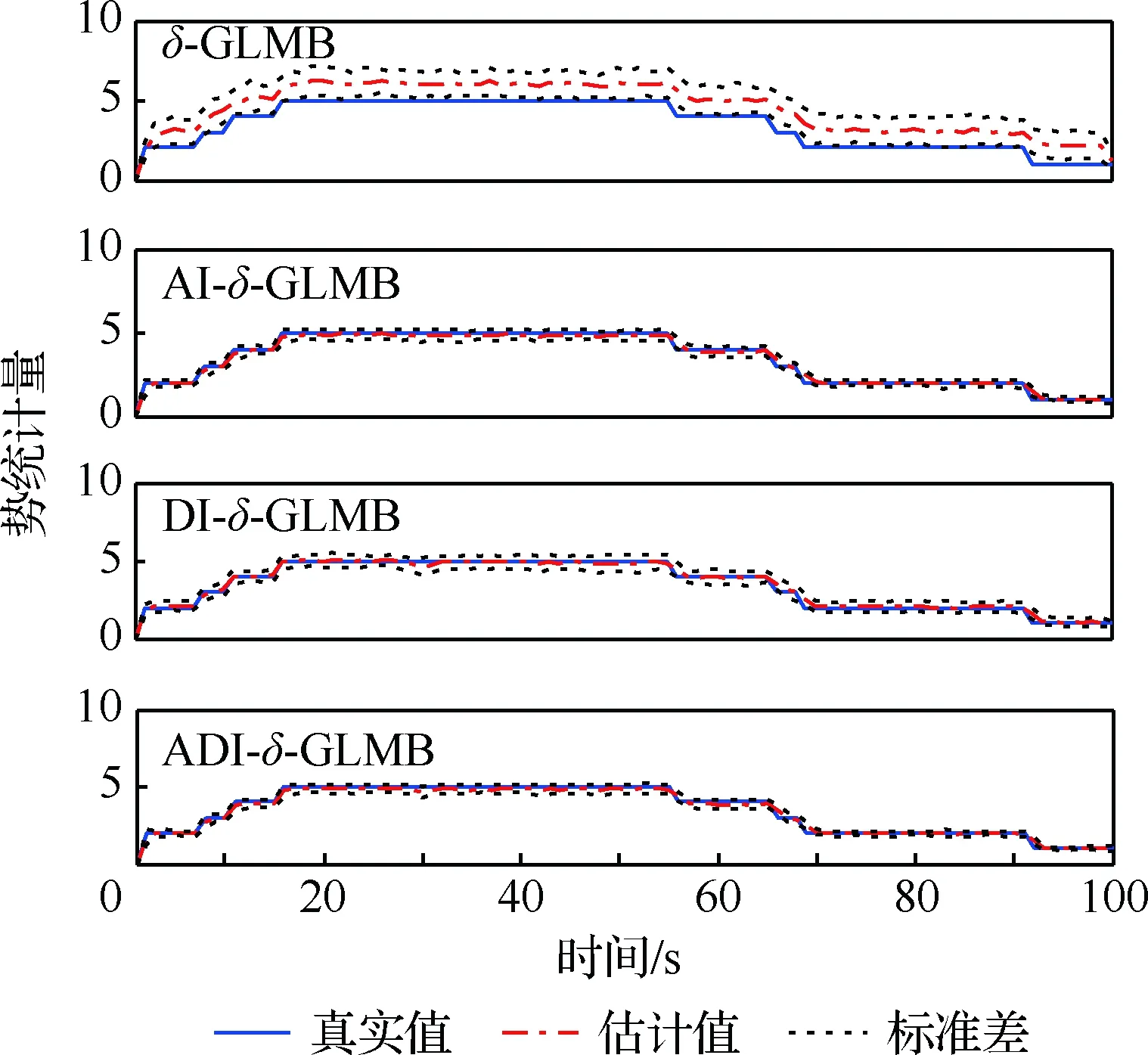
圖2 不同算法勢估計性能對比Fig.2 Comparison of estimated cardinality with different algorithms

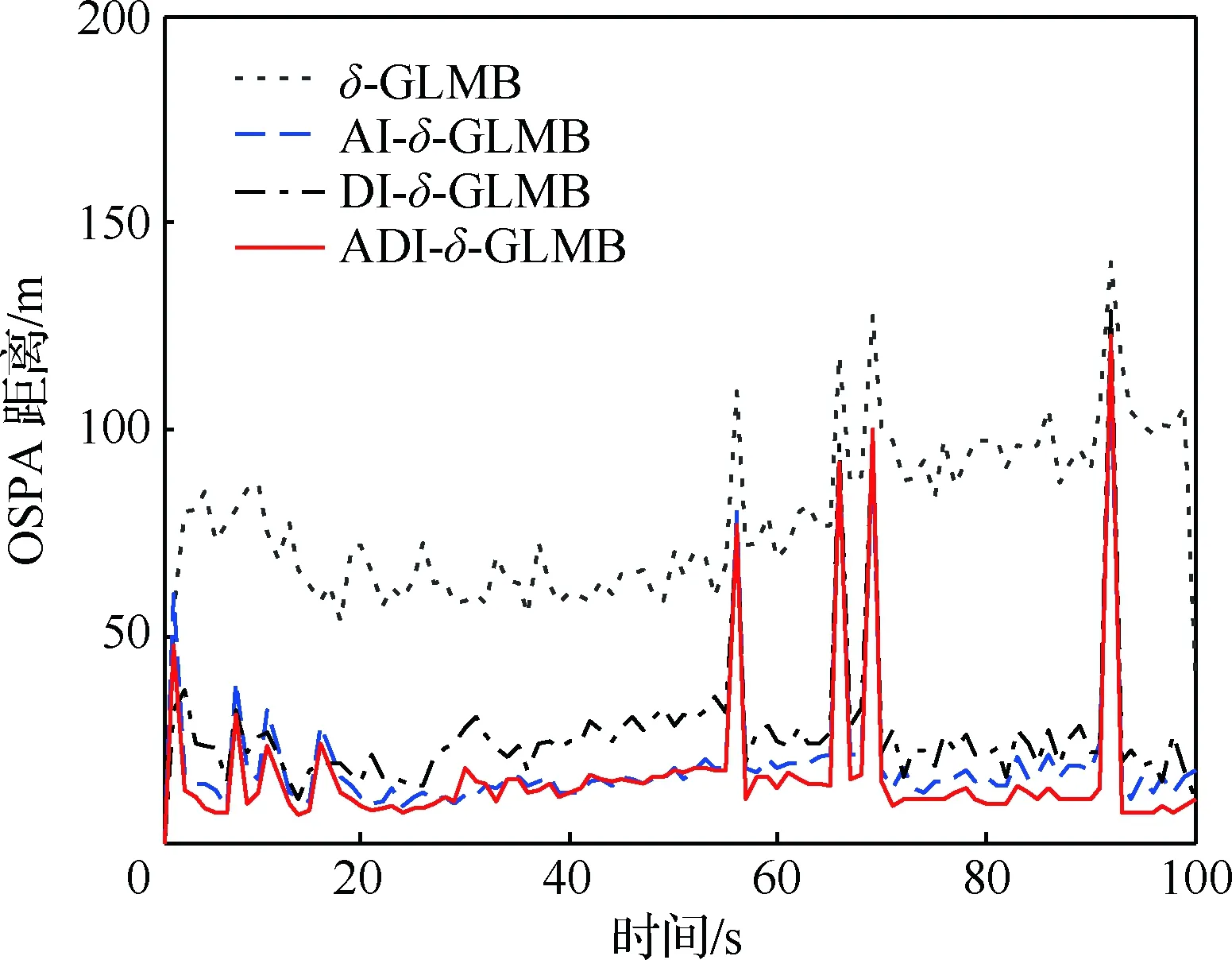
圖3 不同算法的OSPA距離Fig.3 OSPA distance with different algorithms

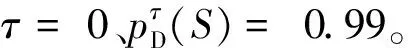
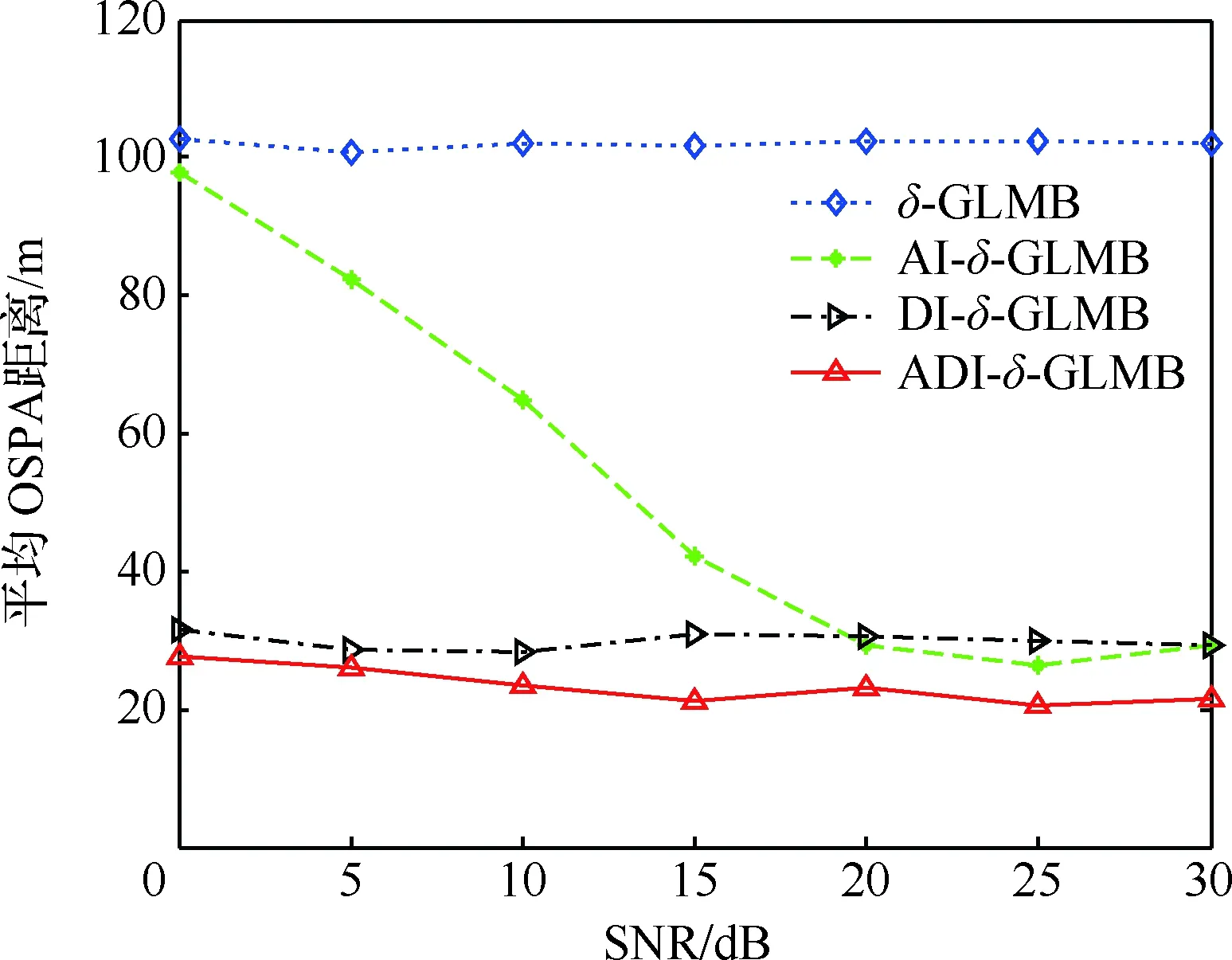
圖4 不同SNR下平均OSPA距離對比Fig.4 Comparison of average OSPA distance with different SNRs

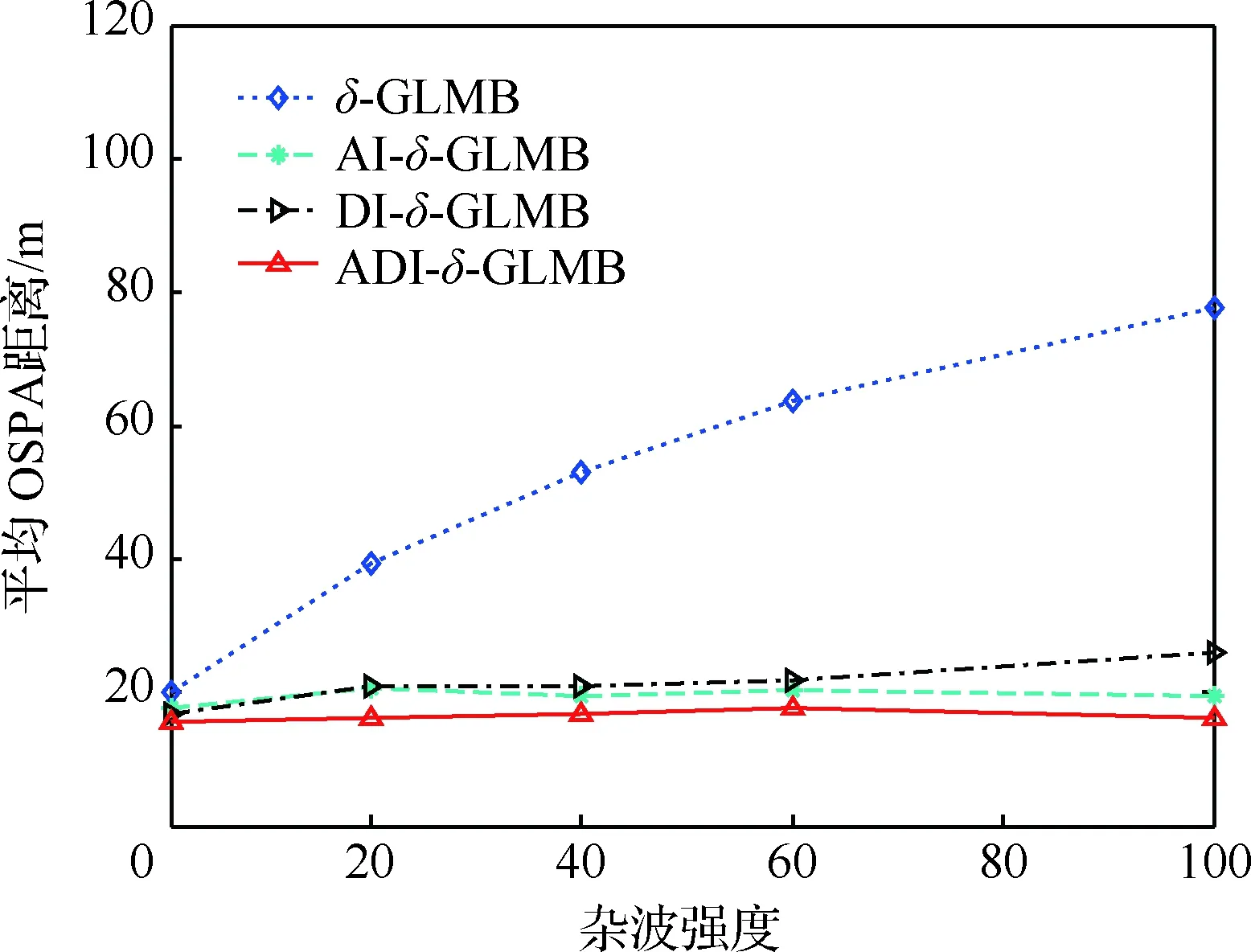
圖5 不同雜波強度下平均OSPA距離對比Fig.5 Comparison of average OSPA distance with different clutter intensity

圖5為不同雜波強度下算法的平均OSPA距離對比。可以看出，隨著雜波強度的增加，標準δ-GLMB濾波器的平均OSPA距離也隨之快速增大，說明其受雜波影響較大；而ADI-δ-GLMB濾波器平均OSPA基本保持穩定，說明其受雜波影響小，抗干擾能力強。

在i5-4590 3.30 GHz CPU，8G RAM，MATLAB 2011軟硬件平臺下，不同雜波強度下算法的平均運行時間對比如圖6所示。可以看出，隨著雜波強度的增加，標準δ-GLMB計算量快速增長，而AI-δ-GLMB、DI-δ-GLMB、ADI-δ-GLMB計算量增長緩慢。這是因為輔助信息的δ-GLMB采用位置、幅度、多普勒的聯合量測似然，利用目標與雜波的幅度及多普勒信息差異，增大了真實航跡假設的權重，并減小了虛假航跡假設的權重，當進行假設裁剪處理時，可去除大量虛假航跡假設，減少需要處理的假設個數，從而降低計算量。

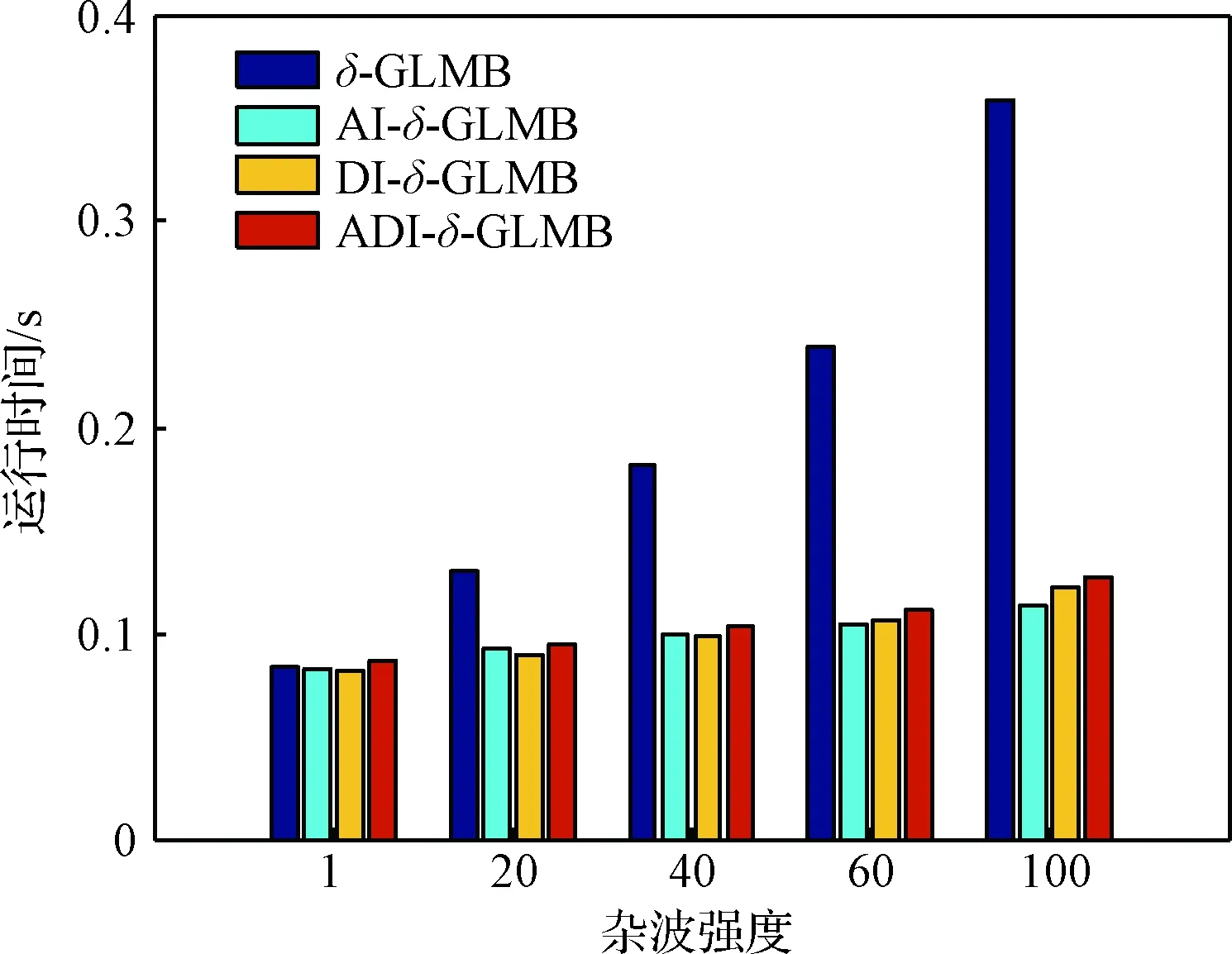
圖6 不同雜波下平均運行時間對比Fig.6 Comparison of average execution time with different clutter

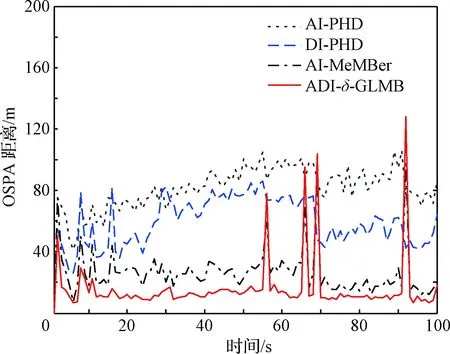
圖7 不同算法的OSPA距離對比Fig.7 Comparison of OSPA distance with different algorithms

為進一步驗證本文算法的性能，在上述實驗條件下，對AI-PHD、DI-PHD、幅度信息多目標多伯努利(Amplitude Information MeMBer, AI-MeMBer)[9]及ADI-δ-GLMB幾種濾波器進行對比。圖7所示為不同算法的OSPA距離對比，可以看出：ADI-δ-GLMB相比其他算法OSPA距離更小，狀態估計精度更高。

4 結 論

利用目標與雜波之間的幅度及多普勒信息差異，提出了一種ADI-δ-GLMB濾波器。

1) ADI-δ-GLMB濾波器能綜合利用幅度及多普勒信息，相比僅利用單一輔助信息，具有更高的跟蹤精度。當利用幅度信息無法對目標與雜波進行區分時，ADI-δ-GLMB會退化為DI-δ-GLMB；當多普勒信息無法獲取時，則退化為AI-δ-GLMB。

2) 引入輔助信息后，有效提高了標準δ-GLMB濾波器的勢估計穩定性及狀態估計精度，并有效降低了高雜波下的計算量，且具有良好的雜波抑制能力；同輔助信息的PHD、MeMBer濾波器相比，ADI-δ-GLMB狀態估計精度更高。