Lipkin-Meshkov-Glick模型中的能級劈裂與宇稱振蕩研究?

喻益湘 宋凝芳 劉伍明

1)(北京航空航天大學儀器科學與光電工程學院,光電技術研究所,北京 100191)

2)(中國科學院物理研究所,北京凝聚態物理國家研究中心,北京 100190)

1 引 言

Lipkin-Meshkov-Glick(LMG)模型最初在核物理中被提出,用來描述核子的集體行為[1?3].近年來,這個模型也被用來描述具有無窮維量子自旋系統的統計物理[4]、腔量子電動力學系統[5]等.1999年,Pan和Draayer[6]用基于Bethe ansatz的無窮維代數方法證明了這個模型是可積的,并找到了其在某些極限下的解析解.另外,LMG模型在熱力學極限下的能譜也具有豐富的結構[7,8].這些研究對了解和應用LMG模型是非常重要的,但是Bethe ansatz方法給出的結果對于計算很多物理量比如關聯函數是沒有用的,另外它們都是基于熱力學極限下的多體理論,而有限尺寸效應在能譜中會呈現出多體系統沒有的特征.最近文獻[9]則對沒有自旋交換相互作用時的有限尺寸LMG模型做了一些解析工作,其中給出了粒子數為2,3,4時的能級表達式.

本文研究了包含N個費米子的有限尺寸的LMG模型,為了獲得它的解,首先將其映射到角動量空間,變成一個約化的LMG模型,其維度從2N變成2J+1.在總自旋守恒的U(1)極限下可以輕易地將哈密頓量對角化,其能譜呈網狀結構;在Z2極限下,能級解析解較復雜,本文采用了量子微擾理論來研究在零塞曼場附近形成束縛態的子能級之間的劈裂行為;而對于更一般的情況,各束縛態將會發生宇稱振蕩行為,本文也給出了宇稱交叉點的臨界塞曼場.同時本文還使用精確對角化獲得了能譜的數值結果,與解析結果形成對照.本文還通過調節相互作用參數呈現了系統從U(1)到Z2的渡越.

2 LMG模型

LMG模型描述的是N個費米子的系統,它們分布在兩個N重簡并的能級上,兩能級之間的能量差為h(下文會看到,這個能量差有塞曼磁場的意義).可以用贗自旋來描述這兩個能級,分別記為↑和↓,而用i來標記N重簡并中的第i個簡并態,其中i=1,2,···,N.考慮兩類二體相互作用,一個是兩個能級之間成對的不改變各自簡并態的序號的散射,即一對下(上)能級的粒子散射成一對上(下)能級的粒子,或者以自旋的語言來描述,即一對自旋↓(↑)的費米子散射成一對自旋↑(↓)的費米子,所以這一項引起自旋z分量不守恒,用V來標記其強度;另一個是自旋交換相互作用,是角動量守恒的,用W來標記其作用強度.這樣,整個系統的哈密頓量表達為

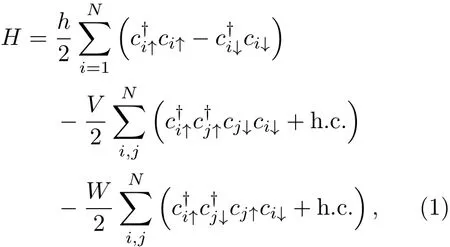
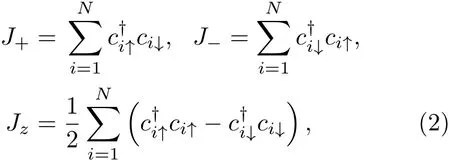
它們滿足角動量的對易關系[Jz,J±]=±J±,[J+,J?]=2Jz.(1)式可以重新寫成

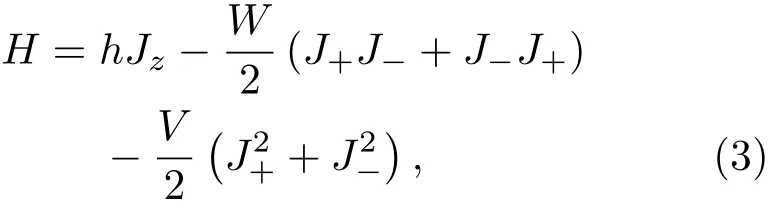
選取J2與Jz的共同本征態為基矢,

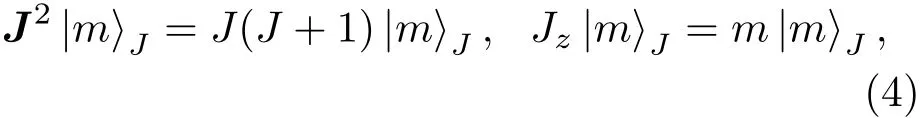
其中,m=?J,?J+1,···,J;Jz是角動量的z方向分量.可以看到宇稱算符

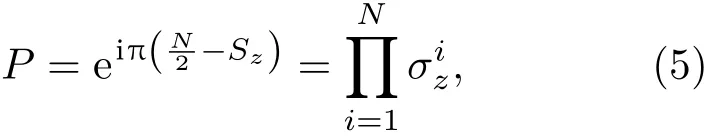
是個守恒量,即哈密頓量(3)有一個Z2對稱性.當V=0時,(3)式有一個U(1)對稱性,即在變換下,哈密頓量保持不變.接下來,本文將詳細分析哈密頓量(3)的能譜結構和物理特征.

3 結果與討論

首先,來看兩個極限的情形.

一個是U(1)極限,V=0,哈密頓量在基矢|m?J下是對角化的,本征能量為

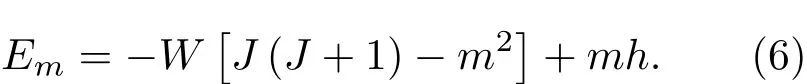
能級結構如圖1所示,可以看到N+1個能級相互交織成網狀,交點很容易算出,比如基態就是被Em與Em+1相交的N個交點隔開,所以容易得到交點處有

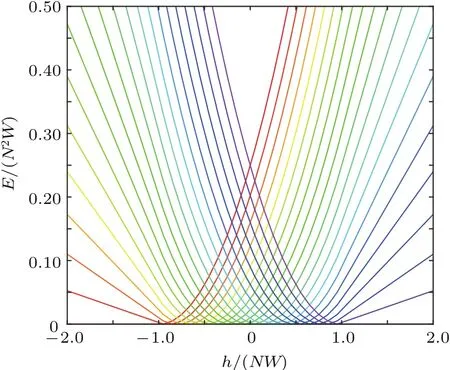
圖1 U(1)極限下,LMG模型的能級分布圖(這里,基態的能量已經從能譜中扣除了,所以基態能量對應于零,顏色從紅色到紫色的線條依次對應于m從J變到?J,這里取N=2J=20)Fig.1.Energy-level structures of LMG model in the U(1)limit.Here,the ground-state energy has been subtracted from all levels.Different colors of levels denotes different values of m,where red is for m=J,violet is for m=J and so on,where N=2J=20.

隨著塞曼場由負逐漸變到正,基態也會經歷N次能級交叉,基態各段對應的m也會從J變到?J.更高能級的交叉點也同樣滿足(7)式,只是交點數量逐漸減少.

另一個極限稱為Z2極限,對應于W=V的情形,系統的哈密頓量變成

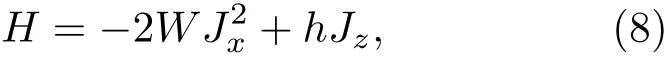
顯然Jz不再是一個守恒量,即系統沒有U(1)對稱性,只有一個Z2對稱性,此情形下能級結構如圖2所示.可以看到在h=0附近,各能級都是由一個奇宇稱和一個偶宇稱的態形成的二重簡并束縛態.這里需要分成兩種情況,對于N為奇數,經過零點時宇稱會發生交叉,比如在h>0和h<0兩端,系統的基態有不同的宇稱,這是很好理解的,只需看|h|?W時,系統在兩端對應的基態分別是m=?J和J,而這兩個態是具有不同宇稱的,所以相應的兩個子能級一定會發生交叉;而對于偶數N,對應的兩端的基態m=?J和J具有相同的宇稱,所以兩子能級不交叉.

那么,構成一個束縛態能級的兩個不同宇稱的子能級之間的劈裂是怎樣在h=0處,趨近于零的呢? 要回答這個問題,需要對于h?W做微擾理論.顯然,h=0時,哈密頓量的本征能量很容易得到,它們就是mx=±J,±(J+1),···對應的個能級,這里?···?表示向+∞取整,對于偶數N,最上面的能級是沒有簡并的,而其余的能級都是二重簡并的.做微擾計算時,要將形成束縛態的兩個無微擾子能級通過微擾項hJz聯結起來才能給出能隙的貢獻,所以只有考慮到2|mx|階的微擾才能得到一個不為零的修正,也就是說,兩子能級之間的間隔具有h2mx的行為,這也解釋了奇數N時發生能級交叉的原因,由于2mx是奇數,對于h>0和h<0兩邊能隙具有不同的符號,而偶數N則有相同符號.

接下來計算Z2極限時的能級劈裂.以基態為例,形成束縛態的兩個無微擾子能級是|J?J與|?J?J(為書寫方便以下略去了下標x,但要注意這不是Jz的本征態),微擾項是H′=hJz,顯然零階的修正是零,而二階和其他高階的修正項對于兩個能級都是一樣的,不能打開能隙,直到2J階的修正才有非零的非對角項出現,這個非對角修正的計算如下:

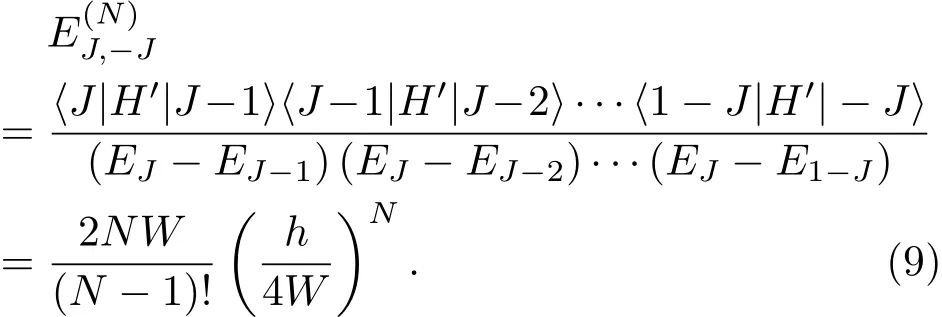
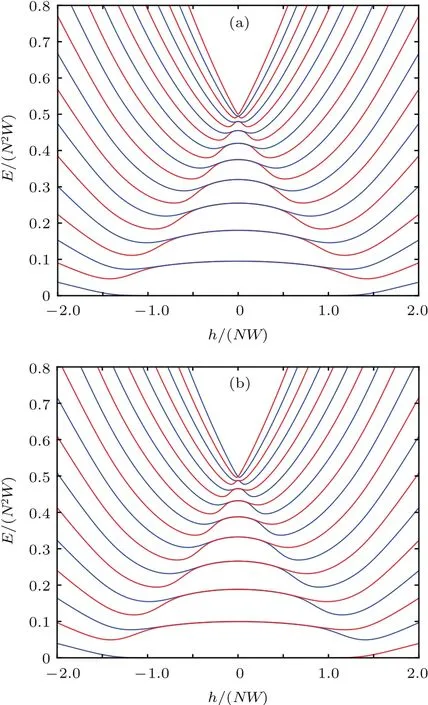
圖2 Z2極限下,系統能級分布圖(紅色代表偶宇稱能級,藍色代表奇宇稱) (a)N=20;(b)N=19;可以看到由于奇偶不同,它們呈現明顯差別,(a)的各束縛態的子能級不交叉,而(b)則會發生宇稱交叉,如(b)的基態在h<0具有偶宇稱,而在h>0具有奇宇稱Fig.2.Energy-level structures of LMG model in the Z2limit.Here,the ground-state energy has been subtracted from all levels.Red lines denote levels with even parity,while blue lines denote levels with odd parity:(a)For N=20,two levels with opposite parities in each bound state get touched without crossing at h=0;(b)for N=19,two levels with opposite parity in a bound state cross each other at h=0,e.g.the parity of ground state is even at h<0 and odd at h>0.

同樣另一個非對角項也是一樣,所以對角化后

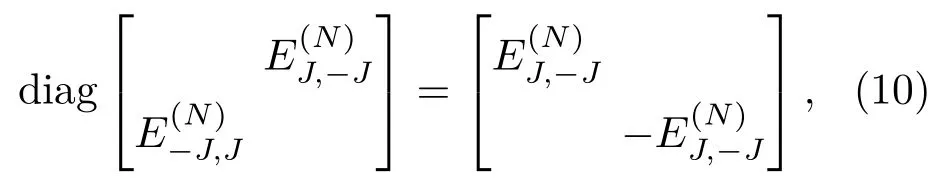
分別對兩個子能級提升和降低, 所以能隙大小為

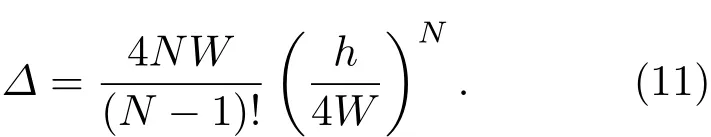
對于激發能級,也可以做類似的微擾計算,不再贅述.

離開上述兩個極限,對于一般的情況W與V不相等,結果又是如何？系統仍然只有Z2對稱性,它不同于U(1)的情況,相同宇稱之間的交叉不再發生,給定一個任意小的V都能使相同宇稱之間的能級交叉打開能隙,而不同宇稱之間的交叉繼續存在,但是交點位置會隨著V的不同而移動.如果重新來觀察基態,就會發現隨著塞曼場的連續變化,基態會在奇偶宇稱之間來回振蕩,這個現象在另一個系統——光學腔Dicke模型中也有發現[10],所以說明它是普遍存在的.圖3給出了不同的V對應的能級圖,可以看到系統是如何從U(1)極限逐步地過渡到Z2極限的.隨著V由零逐漸增大到W,各個束縛態的能隙不斷減小,而子能級之間的交叉點不斷向零點靠近,而有幾個交叉點就對應于Z2極限下,能隙是h的幾階無窮小.通過計算發現在v=W時,奇偶能級之間的交點仍然可以解析地得到

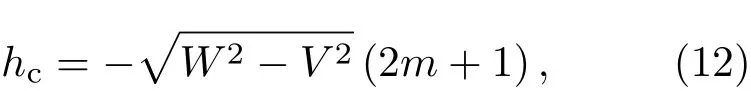
這與U(1)極限的交點位置也是一致的.

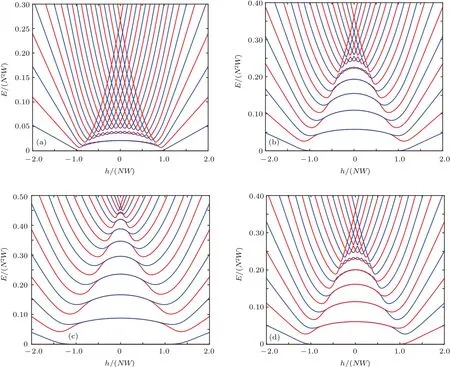
圖3 V取不同值時的能級圖 (a)N=20,V=0.1W;(b)N=20,V=0.5W;(c)N=20,V=0.9W;(d)N=19,V=0.5WFig.3.Energy-level structures for different values of V:(a)N=20,V=0.1W;(b)N=20,V=0.5W;(c)N=20,V=0.9W;(d)N=19,V=0.5W.

4 結 論

LMG模型在包含核物理在內的多個領域都有廣泛的研究價值.模型看似相對簡單,實際上蘊含著許多深刻的物理,自提出以來,不斷有新的研究結果出現.比如,清華大學的Huang等最近利用大N展開的方法研究了有限尺寸的LMG模型的自發對稱性破缺動力學行為[11],發現該系統與Wilczek提出的破缺時間平移對稱性的時間晶體[12,13]的概念極其相似,激發態的壽命是格點數的三次方形式.本文從能級結構的分析入手,發現了U(1)極限、Z2極限,以及介于它們之間更一般情況下的物理特征,在解析和數值兩個方面呈現出了系統的能級劈裂行為,以及宇稱振蕩現象.尤其是宇稱振蕩,我們之前已經在一個原子與光子糾纏的模型中發現了這一現象[10],該模型中驅動這種宇稱振蕩的不是塞曼場,而是原子與光子之間的耦合強度,而本文在一個完全不同的模型中再次出現宇稱振蕩效應,可能也暗示了它們之間存在某種聯系.除了以上兩個系統,我們發現早在十幾年前,在一個描述分子磁體的雙軸自旋系統中[14?16],研究者就已經發現了類似的宇稱隨外場振蕩的效應,他們采用的是費曼路徑積分的方法得到相關結果,與本文的數值和微擾論的結果一致.因此,我們認為宇稱振蕩現象是普遍存在的,未來如果在更多系統中發現這一現象,應該能總結出其一般規律.目前,已經有一些實驗方案被提出,用來模擬LMG模型,比如用光學腔量子電動力學的方法來模擬有耗散的LMG模型[5,17],又如用金剛石中的NV色心來模擬LMG模型中的自旋[18],并使用微波來調控自旋之間的相互作用,以及用光學腔中的玻色-愛因斯坦凝聚體誘導LMG模型[19].但是該模型仍然沒有真正在實驗室實現.LMG模型之所以被研究半個世紀還熱度不減,正因為其中還有許多未被探索的物理,而已經發現的效應對其他方向的研究也具有啟發意義.