用于深空通信的載波同步技術
魏苗苗,劉洲峰,王竹剛
(1.中原工學院電子信息學院河南鄭州451191;2.中國科學院國家空間科學中心,北京100190)
深空通信[1]由于其遙遠的傳輸距離和特殊的運動情況,對通信接收機系統有著很高的要求。在接收和遙測的過程中,首先要克服深空信道中的各種噪聲帶來信噪比極低的問題,其次火星EDL(Entry,Descent and Landing)階段探測器會處于較高的運動狀態[2-3],因此還需解決高動態適應性問題。
針對低信噪比的問題,近年來國內外學者提出了多種利用譯碼輔助同步算法[4-11],但是該類算法的同步范圍有限;為提高該類算法的動態適用性,文中將改進的頻域移位周期圖法與譯碼輔助算法相結合,設計了一種針對深空通信條件下的同步系統并根據算法特點完成參數設計,實現在低信噪比高動態環境下對載波相偏、頻偏以及頻偏變化率的估計。經仿真,該算法在信噪比1.5 dB、火星EDL動態模型下系統可以實現誤碼率達到10-3以下。
1 系統模型
系統采用LDPC(Low density Parity Check Code,低密度奇偶校驗)編碼方式,譯碼算法使用置信傳播(BP)譯碼方式,調制方式為BPSK,噪聲選擇高斯白噪聲(AWGN)。
當信號的高階多普勒變化率較小時,可以恒變化率模型來分析接收信號頻率,即多普勒變化率為常數,此時的接收信號等價于線性調頻信號,可表示為[13]:

采用零中頻接收系統,則中頻信號可表示為

式中:A為接收信號幅值;θk=[2qk+(1+(-1)M2)/2]π/M,qk∈{ }0,1,...,M-1為MPSK調制相位;fd為多普勒頻偏;a為多普勒變化率;n(t)為零均值的高斯白噪聲,方差為σ2。
針對殘留的頻偏和相偏成分,聯合算法采用改進的頻域移位周期圖法進行載波頻偏估計,采用譯碼輔助同步算法實現相偏估計。具體系統總體實現框圖如圖1所示。

圖1 系統總體實現框圖
2 去符號頻域移位平均周期圖法
頻域移位周期圖法[13-14]采用多速率頻域移位運算得到不同支路的頻譜信息,選擇最大值所對應的支路和頻譜位置作為頻偏和頻偏變化率的估計值。去符號頻域移位周期圖法以符號周期的一半作為FFT運算長度,削弱符號跳變對信號頻譜的影響,進一步提高了算法估計性能[16]。算法原理框圖如圖2所示。
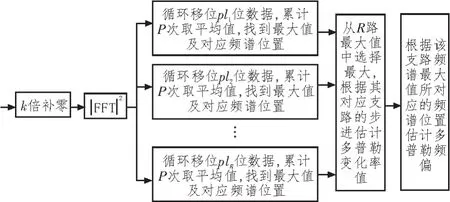
圖2 頻域移位平均周期圖法原理框圖
圖2中:p=1,2,…,P為累計次數。各匹配支路單次循環移位數l1,l2,…,lR分別與原算法中各支路時域匹配因子的a1,a2,…aR相對應。設系統采樣率為fs,單次取樣點數為N,二者對應關系為:

各匹配支路功率譜中sinc函數沿頻率軸移動速率為ΔarT,在預設ar與實際a最接近時,ΔarT為最小,經過累加后,其對應的功率譜在真實頻率附近累積,這也是該算法可工作于極低信噪比下的原因。經比較選大,可粗估計載波多普勒變化率及頻偏,使頻偏和變化率估計誤差降到后級跟蹤算法要求范圍內。
設信號多普勒頻偏范圍為[fdmin,fdmax],變化率范圍為[amin,amax],基帶碼速率為Rb,調制方式為BPSK,后級載波跟蹤對前級載波粗捕獲的精度要求是頻偏不超過fpre,變化率不超過apre,捕獲概率達90%以上,捕獲時間盡可能短。參數設計步驟如下[16]:
1)采樣率fs:為保證大頻偏范圍內信號均能被正確采集,需滿足fs≥2(fdmax-fdmin)。
2)astep:根據apre要求,匹配支路變化率步進astep≤2apre,為降低計算復雜度,取astep=2apre,根據[amin,amax],確定a1,a2,…,aR,R為總匹配支路數。
4)累加次數P:P值的增加可以提高接收信號信噪比,提高捕獲概率,但是過多的累加次數會造成系統計算負擔。針對極低信噪比,需保證P次累加,信號頻率能夠跨過一個頻率分辨率區間,即因此可得,這只是P取值的下限,可根據實際應用要求,兼顧運算量和捕獲概率,進行P值選擇。
5)補零倍數k:補零是為了增加多普勒頻偏估計的頻率分辨率,為使單次移位最小的匹配支路的每次可移位半個頻率分辨率,k值選取應滿足:

此外,為滿足FFT的2n點數要求,k的取值應為2n-1。
3 譯碼輔助載波同步算法
3.1 LDPC譯碼
LDPC碼是一種線性分組碼,需要通過構建校驗矩陣H實現對信息比特編碼。區別于其他奇偶校驗碼,LDPC碼的H矩陣必須為稀疏矩陣并且譯碼方式采用迭代譯碼。根據H矩陣中1的分布規律,可以分為規則LDPC碼和非規則LDPC碼,碼長為n的規則LDPC碼可以表示為(n,j,k),它的校驗矩陣H每列有j個1,每行有k個1,而且任意兩行不能在相同的位置同時為1,且j≥3;非規則LDPC碼表示為(n,m),n為碼長,m為信息位長,校驗矩陣H每行和每列中1的數量不固定[14]。
采用BP譯碼方式,校驗矩陣H定義:設與第n個校驗節點相連的變量節點m的集合為M(m)={m:Hn,m=1};與第m個變量節點相連的校驗節點n的集合為N(n)={n:Hm,n=1}。L(cn)為信號解映射輸出的信號對數似然比;cn,xn,yn分別為第n個碼元、判決信號和接收信號;rmn,qnm分別為校驗節點n與變量節點m之間傳遞的外信息概率。Qn為對應碼字cn的譯碼軟判決概率;C=[c1,…,cN]T為硬判決碼字向量。則在方差為σ2的高斯白噪聲中,譯碼實現步驟如下:
1)迭代變量初始化

2)節點信息更新及迭代過程
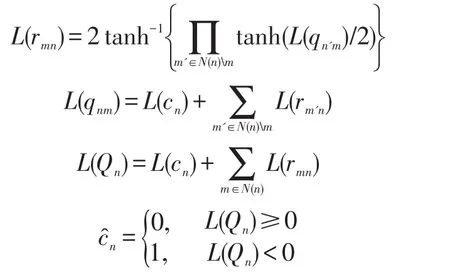
其中,為cn的估計值。若或者迭代次數達到設定的迭代次數,則為譯碼結果,迭代結束;否則轉至2)繼續迭代,直至條件滿足。
3.2 譯碼輔助相偏粗估計
經過多次迭代,譯碼器可以計算出當前碼字的對數似然比L(Qn),L(Qn)是譯碼可靠性的度量值,其絕對值越大,表示判決越可靠。當存在載波頻偏和相偏時,信號需要乘以相位偏移項,使接收信號的有效幅值降低,同時引起所有碼字L(cn)下降,由此得到軟信息絕對值的幅度也將降低。所以譯碼輸出對數似然比信息的大小不僅是譯碼可靠性的表征,也是載波同步優劣的判斷標準[8]。
選擇所有碼字軟信息絕對值累加后作為載波頻偏、相偏估計的代價函數:

其中,上標l表示迭代次數,Δf、θ分別表示在該載波偏差下目標函數、LDPC碼外信息和對數似然比的值。由于改進的科斯塔斯環法的有效相偏估計范圍為(-π/6,π/6),改進的頻域移位周期圖法只能完成頻偏及其變化率的估計,因此需要利用譯碼輸出軟信息對載波相位進行粗估計:分別以載波相位±2π/3,±π/3和0對接收信號進行補償,并根據補償后的譯碼信息計算代價函數,選擇最大值所對應的相位值作為相位粗估結果。
3.3 LDPC譯碼輔助costas環法
設接收信號采樣向量為r=[r0,r1,…rN-1]T,經線性化,得到簡化對數似然函數:

其中,αn表示第n個傳輸符號cn在接收向量為r和相位偏移向量為θ條件下的后驗期望值,可由LDPC譯碼器軟判決輸出求得(BPSK調制方式):

根據最大似然估計準則,可以實現載波頻相偏估計。
為求式(5)最大值,對其進行求導并去掉與參數無關的項得到:

則對應每個碼字的誤差信號為:

將誤差信號輸入環路濾波器,對NCO進行校正:
譯碼軟信息輔助迭代載波同步過程如下:
算法迭代過程:
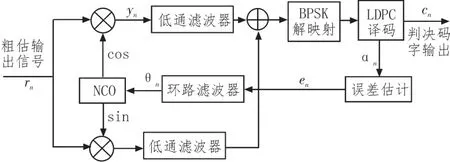
圖3 譯碼輔助載波同步原理框圖
3)環路濾波采用二階濾波結構,γ為迭代步進:
5)如果達到最大迭代次數,則停止迭代,輸出碼字。
4 仿真結果和分析
整個系統的仿真條件設置如下:AWGN信道;采用BPSK調制方式,符號速率Rb=20 bps,采樣率fs=800 kHz。設信噪比EbN0在0~2 dB內變化,多普勒動態模型參考火星探測器進入階段[2]的接收信號動態模型,多普勒頻偏fd∈(-300,300)kHz,變化率a∈(-800,800)Hz/s,相位偏差θ∈(-π,π)。信號fd、a、θ在設定范圍內隨機產生。
細同步部分及編譯碼參數設置:采用1/2碼率的LDPC 碼(2048,1024);LDPC 譯碼的迭代次數最大為20次;用于載波恢復軟信息計算的迭代次數為3次;以10幀數據對細同步進行初步仿真:

圖4 Eb/N0=1.5 dB、θ=π/6時不同頻偏和變化率下譯碼輔助科斯塔斯環法的誤碼率
根據細同步仿真結果可知,在Eb/N0=1.5 dB時,可實現誤碼率低于10-3的載波頻偏有效矯正范圍是,據此設置粗同步部分參為:astep=50 Hz/s,R=32,N=20000,fpre≤100 Hz,apre≤100 Hz/s。對不同累加次數和不同補零倍數進行仿真,結果如圖5所示。

圖5 不同信噪比情況下,累計次數和補零倍數對捕獲概率的影響
由圖5可知,隨著補零倍數和累積次數的增加,捕獲概率相應增大。當累加次數p=50、補零倍數為k=32時,可保證Eb/N0=1.5 dB情況下捕獲概率達到90%。故設定累加次數p=50、k=32,以1000幀數據,對組合算法進行仿真:

圖6 不同信噪比和頻偏下,組合算法誤碼率性能
由圖6,在比特信噪比為1.5 dB時,聯合算法可使系統誤碼率達到10-3,與理想同步誤差不超過0.1 dB,并且保證頻偏估計范圍(-300,300)kHz,相偏估計范圍(-180°,180°),頻偏變化率范圍(-800,800)Hz/s。
5 結論
針對深空通信系統的極限應用條件,本文采用改進的頻域移位周期圖法極大地擴展了有效接收信號的動態范圍,并通過與譯碼輔助的迭代載波同步算法相結合,提高了載波偏差估計的精度,且根據初步仿真結果設計算法參數。經驗證,組合算法可有效工作于極低信噪比高動態的應用環境中。

