基于改進型ELM的指靜脈識別算法研究

劉勝前 ，張烈平 ，趙 陽 ，孫 旋

（1.桂林理工大學 機械與控制工程學院 廣西礦冶與環境科學實驗中心，桂林 541004；2.桂林理工大學環境科學與工程學院，桂林 541004；3.69225部隊84分隊，和靜 841300）

與一般的生物特征圖像相比，基于人體指靜脈的身份識別系統具有一些獨特的優勢：①非接觸性，靜脈位于體表下面，不會因皮膚污染而影響靜脈圖像的采集；②活體性，只有手指或手掌處于活體時才存在成像特征，不會發生類似指紋生物特征的盜用現象，而且身體內部的血管特征很難偽造或是手術改變；③易接收性，圖像采集比較友好，相比DNA和虹膜，讓人心理上更容易接受；④易與其它生物識別技術如人臉、指紋等組成多模生物識別系統[1-4]。

目前對指靜脈身份識別方法的研究主要集中在指靜脈圖像采集、指靜脈圖像特征提取和匹配2個方面。受到手掌皮膚的遮擋、手掌位姿、背景光照、對比度等影響，指靜脈圖像分辨率和清晰度較低，在進行識別時具有一定難度。目前指靜脈圖像特征提取和匹配主要分2類：一類是利用指靜脈圖像的結構特征 （如靜脈紋路圖像的端點和交叉點）來識別指靜脈，這類方法對手掌姿態變換比較敏感，且耗時長[5-7]；另一類主要提取全局靜脈圖像的統計特征來進行識別，這類方法容易丟失圖像局部信息，識別率不高[8-10]。

PCA作為一個非監督學習的降維方法，能夠提取數據中的核心成分，用數據里最主要的方面來代替原始數據。在利用PCA對指靜脈數據進行處理時，僅僅需要以方差衡量信息量，不受特征集以外的因素影響，主要運算是特征值分解，易于實現，可提高檢測時間。由于各主成分之間正交，消除了收集靜脈數據時手指位置可能會移動產生影響，提高檢測準確性。

在進行識別時，神經網絡模型憑借其較好的魯棒性和容錯能力成為圖像分析中的一個熱點研究方向[11-12]。BP神經網絡算法是傳統的手勢識別方法之一，主要通過誤差反向傳播方式來建立手勢識別模型。然而BP方法需要多次迭代才可獲取最優解，無法滿足手勢識別的實時性要求。此外，當梯度下降步長較小時，BP方法容易陷入局部極小值，降低了識別的準確性。

極限學習機是近年來興起的一個新型生物學習網絡[13-14]，具有良好的泛化能力，在利用ELM進行指靜脈分析時，對研究對象數學模型的精確度和性能特性要求均不高，只需要對一定數量的樣本展開訓練和學習就可以完成對指靜脈的識別，具有計算簡單、學習速度快的特點。傳統ELM算法隨機設定輸入和隱層參數，僅采用偽逆算法估計輸出權重，存在容易過學習、算法泛化能力低的問題。本文提出一種PCA特征提取和超限學習機分類相結合的高效指靜脈識別方法，將經過PCA降維提取的最優指靜脈圖像特征信息作為特征向量輸入ELM進行訓練。其次在傳統ELM基礎上，在估計輸出權重時引入L1范數約束來控制整個模型的復雜度，引入L2范數約束來提高模型泛化能力。不僅大大降低了要處理的樣本數量，又保持了ELM學習速度快、精度高的優點。

1 基于PCA-ELM的靜脈識別方法

1.1 圖像預處理

1.1.1 靜脈圖像的增強

由于平滑處理后的圖像中靜脈血管可能會比較模糊，不利于后續處理，因此需要對圖像進行增強。針對靜脈圖像整體過暗的特點，采用提升灰度值的思想，使用對數灰度變換法[15]。對數灰度變換法的公式如下所示：

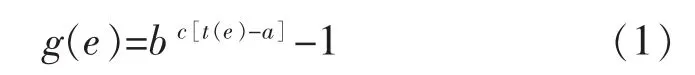
式中：e表示灰度相關變量；t（e）是原始圖像灰度函數；g（e）是轉換后的圖像灰度函數；b和c是用來調整曲線的位置和形狀，b用于控制曲線形狀，c用于控制變換速率；a相當于平移量，在灰度沒有達到a時皆將輸入定位為0。

1.1.2 靜脈圖像的分割

針對每一個像素點f（x，y），都有一個對應的灰度閾值T（x，y）。利用一種基于圖像統計的閾值選取方法來對原始指靜脈圖像進行分割[16]。閾值計算公式為

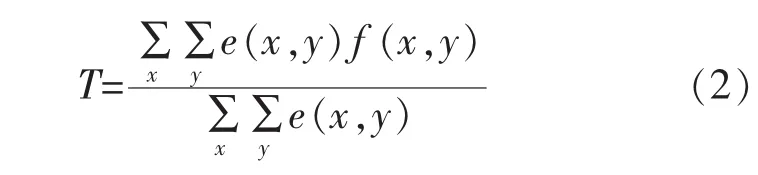
其中：

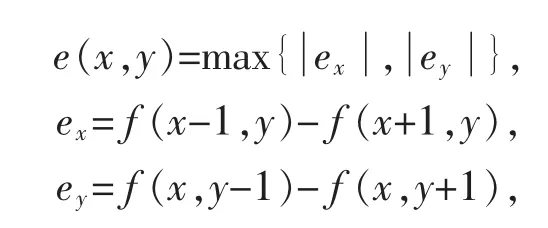
圖像預處理結果如圖1所示。

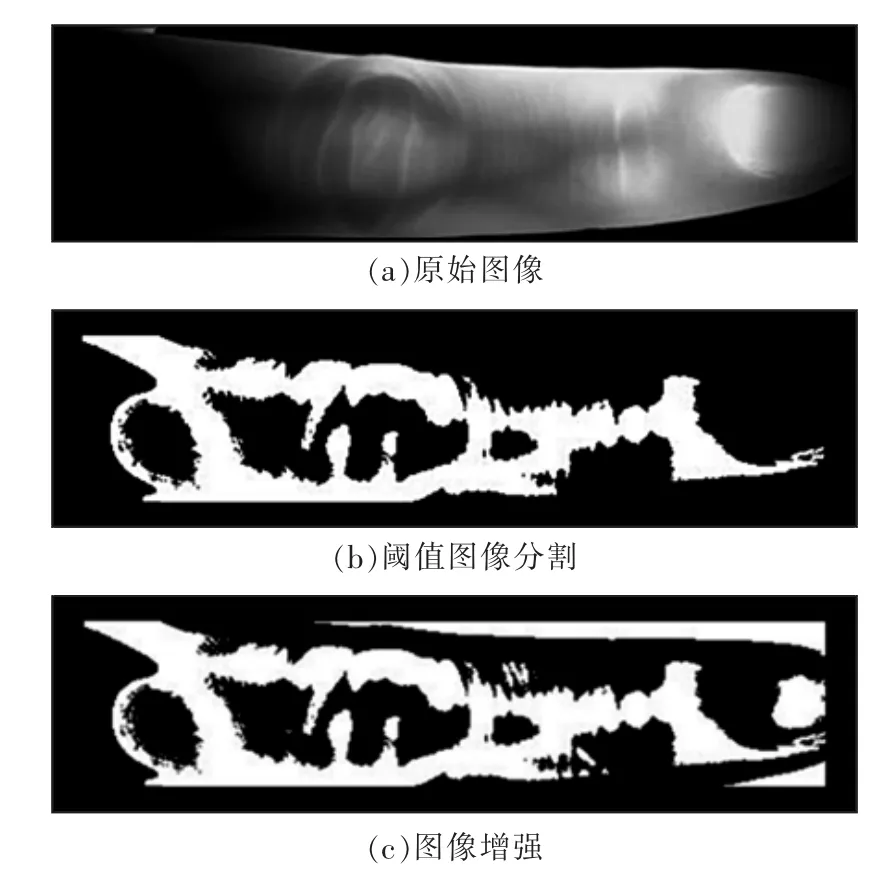
圖1 預處理結果Fig.1 Pretreatment results

1.2 基于PCA的靜脈圖像降維

首先建立樣本的協方差矩陣R：

式中：Λ=diag（λ1，λ2，…，λL），λ1≥λ2≥…≥λL為樣本相關矩陣；U=［u1，u2，…，uL］為與樣本相關矩陣中特征值對應的特征向量矩陣。定義主元方差貢獻率：

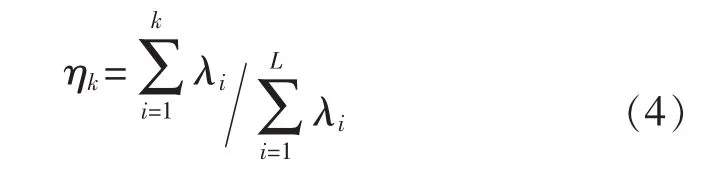
計算前k個主元的方差貢獻率，選取使貢獻率ηk≥85%的主元為最終主成分，并利用所選的主成分特征值對應的特征向量構建變換矩陣K=［u1，u2，…，uk］，k＜L。 新的樣本空間 A=（a1，a2，…，aN）T可以通過A=XK來進行重構。重構后的樣本不僅消除了靜脈圖像中相關性較強的一些特征，而且達到了降維的目的。

2 基于ELM的指靜脈識別模型

對于N個降維后的靜脈圖像訓練樣本（ai，ti），i=1，2，…，N，其中 ai=［ai1，ai2，…，aiK］∈Rk，ti=［ti1，ti2，…，tim]∈Rm，則一個有T個隱層節點的ELM數學模型可以表示為

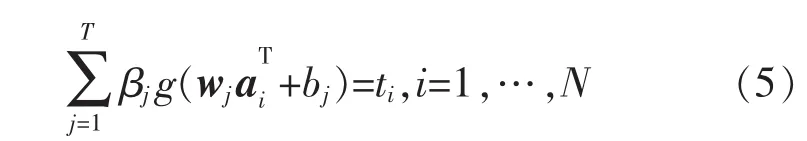
式中：wj=［wj1，wj2，…，wjk］為輸入節點同第 j個隱層節點之間的連接權重；βj為j個隱層節點輸出權重；bj為第j個隱層節點的偏置；g（·）為激活函數。借鑒類腦思維中隨機性思想，ELM算法對于wj和bj均隨機給定，并在整個過程中保持不變，大大節省了訓練時間，提高了算法運算速率。輸出權重βj是ELM中唯一需要解析確定的參數。用矩陣形式重新表示式（3），可以得到：

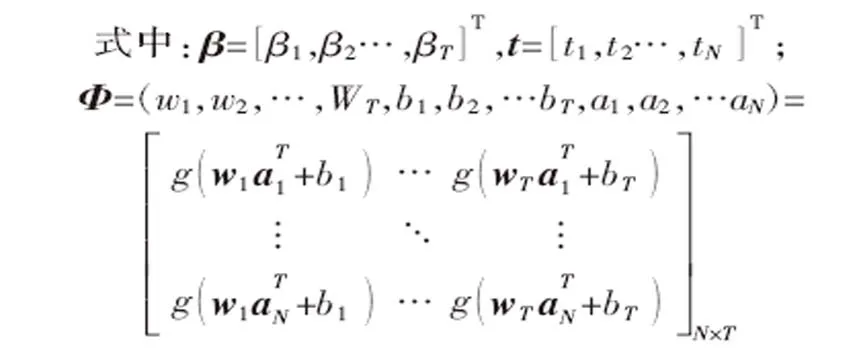
在傳統ELM算法中，輸出權重β通過求解最小二乘問題得到：

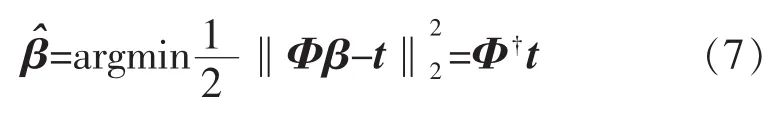
其中Φ?為偽逆，由于最小二乘算法實現簡單，使得ELM算法在計算效率方面明顯優于傳統BP算法。然而在實際數據分析中，發現當Φ存在不適定現象時，輸出權重β幅值會急劇增大，導致過擬合現象，極大影響ELM算法的模型準確性，降低ELM網絡的泛化能力。

為了解決上述問題，在式（7）中加入L1-L2范數約束，一方面憑借L1范數的稀疏能力可以使模型變得簡單，另一方面L2范數約束可以提高算法的泛化能力，得到如下公式：

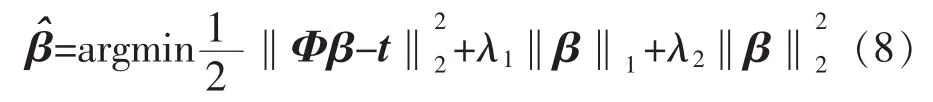
為了方便求解公式（8），定義如下矩陣：

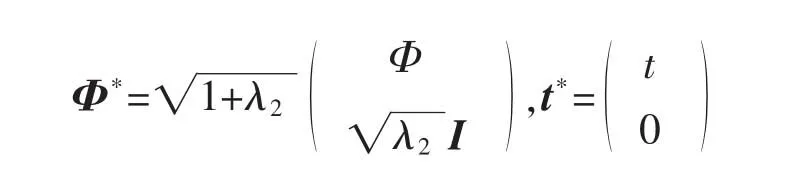
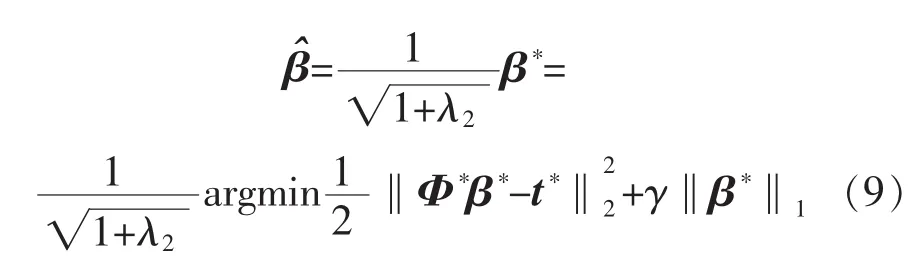
由于λ2為一預先設定的常數，式（9）進一步展開可以得到：

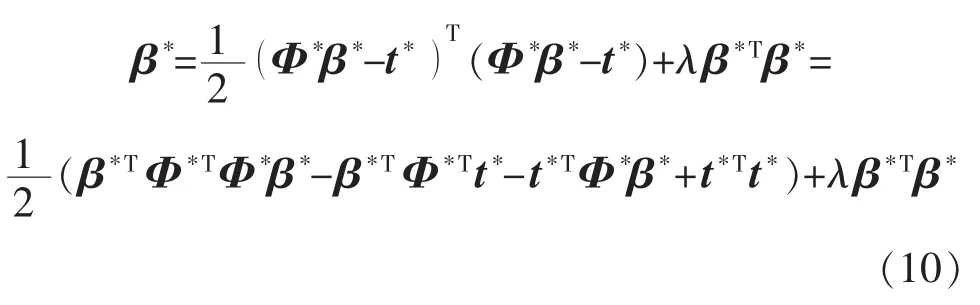
式（10）對β*求偏導，并令導數為零，可以得到：

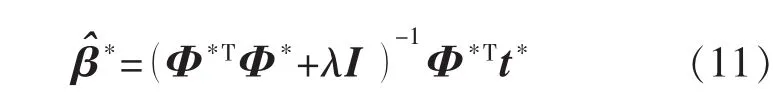
綜上所述，基于L1/L2-ELM算法的步驟可以概括為以下三步：

（1）隨機產生隱層節點參數wj和bj；

（2）計算隱層輸出矩陣Φ；

3 實驗結果分析

為了驗證所提出算法的有效性，選取了自采集數據和來自MMCBNU-6000的公共數據集。公共數據集有來自不同國家、血型、性別和年齡的人群，共100個人。每個人18張指靜脈圖片，其中無名指、中指和食指各6張，共100*18=1800張指靜脈圖片。實驗環境為處理器Inter1.60 GHz，內存1 GB，Matlab12平臺仿真。

圖2展示了PCA前后對指靜脈圖像的預處理效果，可以看出經過PCA操作在降維的同時有效保留了圖像中的靜脈分布。即使在圖像有小角度旋轉的情況下，PCA也可以抓住圖像中的有效特征，一定程度上提升了算法的魯棒性。

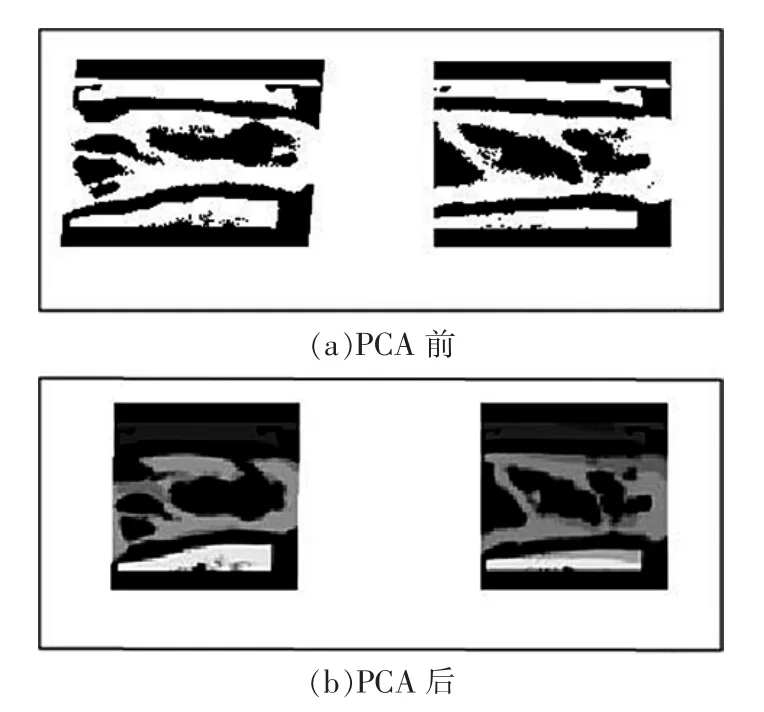
圖2 PCA處理前后的效果對比Fig.2 Comparison of the effect of PCA rendering

如圖3所示，經過三重交叉驗證之后，可以得到對三個不同用戶的身份識別準確率。所提出算法在識別準確率方面占據了明顯的優勢，主要原因在于指靜脈圖像采集過程中極易受到手指姿態、背景光線的影響，會造成圖像細微的旋轉，經過PCA的特征提取，可以減弱甚至消除圖像的負面變化，有利于分類準確率的提高。此外，由于訓練樣本較少，在利用ELM框架進行訓練時極容易發生過擬合，因此采用L1和L2范數約束可以有效避免過擬合，提升算法的范化能力。

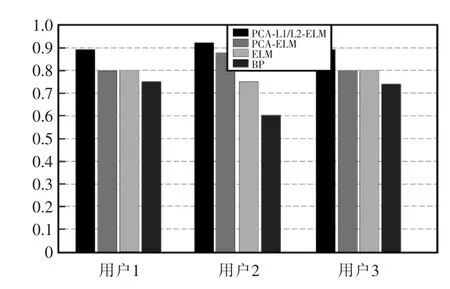
圖3 準確率對比圖Fig.3 Contrast figure of accuracy

ELM網絡在進行分類時，隱層神經元的數目需要人為設定。實驗發現隱層神經元數目對識別結果具有一定影響，為了設置合適的隱層神經元數目，文章分析了當隱層神經元數目從20增加至160時的指靜脈圖像分類準確率，并選取最高準確率對應的隱層神經元數目作為最終隱層神經元數目設定值。此外，表1對網絡規模進行了對比分析，可以發現經過傳統BP網絡訓練時間最長，且準確率較差。與傳統ELM算法相比，經過PCA進行特征提取之后，可以極大縮短ELM網絡的訓練時間。

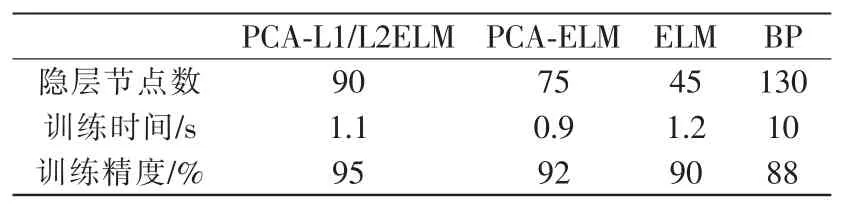
表1 網絡模型規模比較Tab.1 Comparison of network model scale

4 結語

本文在極限學習機的基礎之上，結合主成分分析法，提出了一種PCA-L1/L2ELM的神經網絡算法，本文提出的算法比ELM的訓練時間更短，準確率更高，穩定性更強。一方面通過PCA提取指靜脈圖像的特征信息，使得訓練數據更為簡單，消除了圖像特征之間的關聯度，強調圖像特征個體特性。另一方面結合ELM的快速訓練測試神經網絡，通過在ELM算法中引入L1范數約束來簡化模型，引入L2范數約束來提高模型的泛化能力。實驗結果證明該方法具有準確率高、響應快的優點。