自適應匹配追蹤圖像超分辨算法

華 臻,張海程,李晉江

1(山東工商學院 信息與電子工程學院,山東 煙臺 264000)

2(山東工商學院 山東省高等學校協同創新中心:未來智能計算,山東 煙臺 264000)

1 引 言

圖像超分辨率(super-resolution,SR)重建是指通過圖像處理算法對模糊的低分辨率(low-resolution,LR)圖像進行處理,以獲得高分辨率(high-resolution,HR)圖像,此圖像有高像素密度,可以提供更多的細節信息,能提高計算機識別圖像的準確性.該技術在醫學成像、視頻監控、遙感圖像等領域非常廣泛.

如果考慮噪聲e,低分辨率圖像Y和高分辨率圖像X可以表示為:

Y=SHX+e

(1)

其中,S為下采樣,H表示模糊濾波器.由于LR圖像數量的不足、病態配準問題以及未知的模糊操作,因此SR重建是一個典型的病態問題.要解決這個問題,需要通過合理的先驗知識并獲得某些約束條件來求得最優解.

目前,SR重建技術可以分為三類:基于插值、基于重構和基于學習的方法.其中基于學習的方法是目前研究的熱點[1-7],其基本思想是通過訓練樣本得到LR圖像到HR圖像的映射,從而預測出HR圖像.基于馬爾科夫網絡[3]、局部線性嵌入法[4]、錨定鄰居[5]等大量的學習算法被提出,但是這些方法都有各自的局限性,學習過程中特征提取和表達能力有限.

近年來,稀疏表示理論成為圖像處理領域的研究熱點,在圖像去噪、人臉識別[6]、超分辨率等領域都有廣泛的應用.為了避免人為的進行近鄰選擇,Yang等人從壓縮感知(Pressive Sensing)的理論出發,開創性地提出一種基于稀疏編碼的SR重構算法[7],但是有字典學習效率低,重建效果差等缺點.Zhan等人提出了一種耦合特征空間下改進字典學習的圖像SR重建算法,使用了迭代反投影算法對重建后的圖像進行處理,獲得了不錯的重建效果[8].為了提高稀疏表示系數的精度,文獻[9]在稀疏表示中引入了正則化技術.Zhang等人提出了基于K-SVD算法和半耦合字典學習框架融合的圖像SR重建方法,解決了字典訓練費時問題,同時提高重建質量[10].

這種基于稀疏表示的超分辨率重構算法,需要通過優化算法對稀疏表示模型進行優化.比如:正交匹配追蹤算法(Orthogonal MP,OMP)[11,12]、稀疏度自適應匹配追蹤算法[13]等.其中OMP 算法應用較為廣泛,但是重構時間較長,重構不夠精確.

最近,Vu等人提出一種新的貪心算法,即自適應匹配追蹤(Adaptive Matching Pursuit,AMP)算法[14].本文將此算法應用到SR重建中,進行稀疏優化.在Yang等人提出的稀疏表示框架的基礎上,本文提出了一個基于AMP稀疏表示的圖像SR重建算法.實驗發現,此算法重建效果較理想,特別是在細節重建方面更加突出,成功解決了OMP算法重構不精確的缺點.

2 相關工作

2.1 稀疏表示理論

Zhong和Mallat等人首先提出信號可以在冗余字典上稀疏分解的思想,選取合適的冗余字典可以用來更好的表示信號的基,且基的數目最少,這就是信號的稀疏表示.

假設信號x∈RN可以用過完備字典D∈RN×M(M>N)中有限的原子進行線性表示,即

x=Dα,s.t.‖α‖0≤n

(2)

其中‖*‖0是L0范數,‖α‖0代表向量α的非零元素的個數,稱α為x的 稀 疏 表 示系數.D是包含M個原子的過完備字典,D=[d1,d2,…,dn],D∈RN,di是D中列元素構成的向量,記η為D列向量線性相關的最小值.則當‖α‖0<η/2時,x的稀疏表示系數α是唯一存在的[15].因此,稀疏表示的問題就是求解稀疏表示系數α,即:

min‖α‖0,s.t.x=Dα

(3)

獲得(3)式的精確解被證明是NP難問題,而且是非凸優化問題,通常都考慮其近似解法.研究發現,將L1范數替換L0范數,可以使得上述問題從一個非凸問題轉變成凸優化的問題.目前應用廣泛的稀疏表示模型是:

(4)

其中xi表示每一個訓練樣本,‖αi‖表示每一列的稀疏表示系數,λ是稀疏平衡因子,這樣稀疏優化問題就轉化為凸優化問題,可以用一些標準的優化算法求得α*的解.

2.2 超分辨率重建算法的基本思想

圖像的超分辨率重建算法主要解決,如何將一幅低分辨率圖像恢復成高分辨率圖像的問題.其中有兩個最重要的問題:訓練字典和稀疏編碼.

設x∈RN為提取出來的HR圖像塊,y∈RM為相關的LR圖像塊,都以列向量的形式表示.本次工作就是將HR圖像塊x由字典中的原子線性稀疏表示出來,即x=Dhα,其中Dh為高分辨率字典,相應的低分辨率圖像塊可以表示為y=Dlα+e,Dl為低分辨率字典.

根據公式(4),此問題可以轉化為稀疏向量的α的優化問題,即:

(5)

本文所提出的自適應匹配追蹤圖像超分辨重建算法流程圖如圖1所示.

圖1 自適應匹配追蹤圖像超分辨重建Fig.1 Image SR algorithm based on AMP

3 訓練字典

3.1 K-SVD算法訓練單個字典

字典通常從一組訓練樣本X={x1,x2,…,xt}中學習.對于所有的訓練集,需要求解以下優化問題:

(6)

其中,A的列向量αi為樣本圖像塊的稀疏系數,‖dj‖為字典D的標準化原子,T0為信號稀疏度.求解此類問題通常需要固定其中一個變量來求另外一個變量.

(7)

3.2 訓練聯合字典

超分辨率是嚴重的病態逆問題,為了解決這個逆問題,采用稀疏性這個先驗知識,這個先驗知識要求訓練得到的字典Dh和Dl有較強的同構性.可以通過訓練單個字典達到訓練兩個字典的目的.

假設給出的訓練圖像塊對為P={Xh,Yl},其中,Xh={x1,x2,…,xn}為采樣后的HR圖像塊組,Yl={y1,y2,…,yn} 為相關的LR圖像塊組.根據式(4)可以知道,HR和LR圖像塊空間的稀疏編碼問題分別是:

(8)

和

(9)

要使兩個特征空間有相同的稀疏表示,即αh=αl,公式(8)(9)可以合寫成以下問題[16]:

(10)

其中,N和M是HR和LR圖像塊的維數,寫成訓練單個字典的形式為:

(11)

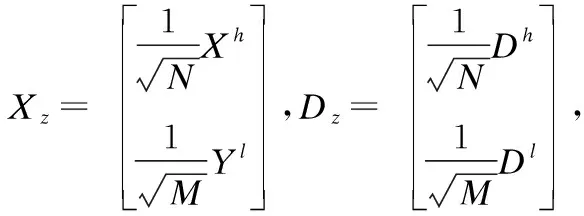
3.3 特征提取

目前提取高頻的方法有很多,Li等人[17]使用高斯邊緣濾波.Tang等人[18]使用LR圖像的一階、二階梯度作來提取圖像梯度信息.由于此方法簡單有效,本文使用將一階、二階梯度作為特征,用來提取的四個濾波器分別是:

(12)

其中T表示向量轉置,這四個濾波器不是直接應用到LR圖像塊中,而是應用到訓練圖像.濾波完成后會得到四個梯度圖.然后從梯度圖像的每個位置提取四個的小塊圖像,將四個小塊圖像連接成一個特征向量,將特征向量作為LR圖像塊的最終特征表示.同時,每個LR圖像塊的特征表示也對其相鄰信息進行編碼,提高SR圖像相鄰圖像塊的兼容性.

4 基于自適應匹配追蹤的圖像超分辨率重建

4.1 自適應匹配追蹤

AMP是解決稀疏表示最為新穎的算法.該算法的基本思想是通過依次迭代的方法更新每一步的稀疏信號的有效集合,然后推導出稀疏表示系數的解.

在每一步中,不斷更新殘差以確定是否吸收或移除集合中的元素.大多數OMP算法需要已知信號的稀疏性,這在實踐中通常是未知的.AMP算法可以自適應地解決這一問題,并且在準確度和效率上都得到了顯著提高.實質上,在算法的每一步中,通過添加或刪除索引來更新元素集時,無論哪個在效率上都有很好的改進.另外,該算法的中間步驟通過簡單的Cholesky分解來計算,這使得算法更快[14].

假設一組稀疏信號α∈Rp,根據y=Dα+e從較少的線性測度y∈Rq中恢復出來,其中q遠遠小于p,D∈Rq×p是測量矩陣,e表示高斯噪聲.

(13)

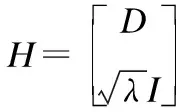
(14)

(15)

AMP 算法描述如算法1所示.

算法1.自適應匹配追蹤AMP 算法

function(α*)=AMP(y,D,λ,ρ)

% ifS=φ,thenL=[]

3. whiletruedo

4. 計算u和αS:LSu=wS,LSαS=u;

5. 更新殘差rS:rS=z-HSαS;

7. 判 斷條件

插入索引S=S∪{i},更新LS;

else 移除索引S=S{j},更新LS;

end if

8. end while

9. 依次更新:αS?α*

end functio

4.2 局部模型重建

通過2.2小節的介紹可知,SR重建的模型表示為公式(5).在實驗過程中,不是直接在低分辨率圖像上操作,而是先加入特征提取算子F用來提取LR圖像上的高頻信息.結合高低分辨率圖像塊間的聯系,將式(5)轉化為:

(16)

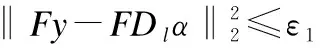
利用拉格朗日乘子法,式(16)可以進一步合寫成

(17)

之后采用AMP算法求解稀疏表示系數α*.通過公式x=Dhα*生成包含高頻信息的HR圖像塊,加上平均像素后得到初始HR圖像X0,但是,這時恢復出的HR圖像僅包含局部高頻信息.

4.3 全局模型重建

稀疏表示的約束并不是一個精確的等式,可能圖像中會有噪聲等污染,因此局部模型得到的高分辨率圖像X0可能不是最優結果.接下來需要通過全局模型重建消除局部模型中的人造結果,使圖像更為自然.

研究發現,將局部模型重建得到的高分辨率圖像X0投影到Y=SHX的解空間上可以消除誤差,即

(18)

此優化問題能夠采用反向傳播算法[20]和梯度下降法來解決.本文使用反向傳播算法進行求解,即通過式(18)進行每一步迭代更新,即

Xt+1=Xt+((Y-SHXt)↑s)×φ

(19)

其中,Xt是HR圖像經過第t次迭代之后的估計值,φ反投影濾波器,s表示上采樣.最終結果X*即為HR圖像的最終估計.

基于AMP的超分辨率重建算法描述如算法2所示：

算法2.基于AMP算法的超分辨率重建

Input:字典對Dh和Dl,低分辨率圖像Y

Output:重建后的超分辨率圖像X*

1. for 來自Y的每一個b×b大小的圖像塊ydo

2. 從左上角開始取圖像塊,每個方向重疊1個像素,計算平均像素p;

3. 調用AMP算法計算公式(20)中的稀疏表示系數α*;

4. 通過公式x=Dhα*生成包含高頻信息的HR圖像塊;

5. 將x加上平均像素p得到初始HR圖像X0;

6. for end

7. 使用反投影算法估計出最終HR圖像X*.

5 實驗結果與分析

5.1 實驗環境

為了驗證本文所提算法的有效性,所有的仿真實驗用Matlab語言編寫,軟硬件的運行環境為:Inter(R)Core(TM)i7-6700 CPU @ 3.40GHZ處理器、運行內存為8GB、64位Windows7 SP1 操作系統、Matlab R2016a.

5.2 數據集

數據集訓練:超分辨率重建所用的方法不同,使用的數據集也有所不同.例如,RFL[21]使用了兩種方法,第一種方法是使用了來自Yang等人[7]的91幅圖像,第二種方法是使用了291個圖像.SRCNN[22]使用了非常大的ImageNet數據集.

可以簡單地從類似的訓練圖像中隨機抽樣原始色塊來生成字典統計性質.本實驗使用來自文獻[21]的圖像進行訓練.準備了兩個字典:一個字典的訓練集是從花中抽取的,應用于具有相對簡單紋理的通用圖像;一個字典的訓練集從動物中抽取的,包括各種人頭、毛發等,具有精細的紋理,能夠更好的重建頭部等精細圖像.

數據集測試:本實驗采用了三個數據集進行測試,分別為:數據集“Set5”[24]、“Set14”和“B100”.數據集“Set5”和“Set14”通常也用于其他作品[5].數據集“B100”是Timofte等人[5]所用的伯克利分割數據集中的自然圖像.

5.3 字典訓練及參數的設置

實驗選取了30幅具有豐富紋理的高分辨率圖像,然后對這些高分辨率圖像2倍下采樣,模擬圖像的降質過程,得到對應的LR圖像.將這些HR和LR圖像,隨機采樣80,000個9×9大小的圖像塊,以訓練字典.利用前面所分析的聯合字典訓練方法,得到高、低分辨率字典.生成字典的大小為1024.

在重建過程中,將輸入的低分辨率圖像利用雙立方插值算法進行2倍上采樣,使用3×3的低分辨率圖像塊(上采樣到6×6),相鄰塊之間有1個像素的重疊,對應的9×9高分辨率圖像塊有3個像素塊的重疊,實驗5.4中也給出了放大2倍、4倍時的結果.對于彩色圖像,由于人類的視覺特性對亮度細節更為敏感,因此僅將算法應用到亮度通道,而色度通道(Cb,Cr)用雙立方插值算法進行計算.算法中的自由參數λ設為0.1,用來平衡稀疏性和重建約束的保真度,σ設為0.018.

5.4 算法對比

實驗中,將本文算法與Bicubic、Yang′s[7]、Fu′s[24]、 CFS[6]、WDM[25]算法進行了重建效果的比較.使用評價指標峰值信噪比(Peak Signal to Noise Ratio,PSNR)和結構相似性(Structural Similarity Index,SSIM)進行定量分析,通過重建效果對比圖進行定性分析.

表1展示了圖像“Set5”、“Set14”和“B100”在不同算法下重建后的PSNR和SSIM值,圖像的放大尺度分別為2,3 和4.從表中可以看出,Bicubic算法的性能最差,其他算法都使用了稀疏表示思想,性能明顯提高,PSNR大約提高1-3db.隨著倍數的增加,算法的PSNR和SSIM都相應的減少.本文算法雖然在放大4倍時性能有所下降,但是大多數情況下,PSNR和SSIM值都高于其他算法.

圖2至圖6為不同算法關于圖像child、lena、boy的效果對比圖.從圖中可以看出,Bicubic和Yang′s重建圖像比較模糊,Fu′s、 CFS和WDM算法雖然有了提升,但是細節上的重建效果不是很理想,而本文算法大大提升了細節上的重建效果,而且重建圖像也較清晰.為了更加清晰地看到不同算法在細節上的重建效果,將效果圖進行了放大,圖2的眼部放大效果圖如圖3所示.可以看出,相比其他算法,本文算法重建后的眉毛更加濃密、眼球更加清晰.圖5是boy圖像的局部放大圖,可以看到,本文算法鼻子上面的紅斑數量比其他算法更多,細節重建效果佳.圖6是lena圖像效果圖,本文算法與CFS、WDM算法效果差不多,能重建出較多的細節,但其他算法圖像模糊且出現鋸齒現象.

圖2 child圖像使用不同算法重建效果對比圖Fig.2 Effect of reconstruction comparisonchart of child image

圖3 child圖像局部對比圖Fig.3 Partial comparison chart of child image

圖4 boy圖像使用不同算法重建效果對比圖Fig.4 Effect of reconstruction comparison chart of boy image

圖5 boy圖像局部對比圖Fig.5 Partial comparison chart of boy image

表1 不同算法在PSNR和SSIM方面的對比值Table 1 Benchmark results.Average PSNR/SSIMs for scale factor 2,3 and 4 on datasets Set5,Set14 and B100

圖6 lena圖像使用不同算法重建效果對比圖Fig.6 Reconstruction comparison chart of lena image

本次實驗從定量和定性兩個方面對算法進行比較,大多數情況下,本文算法的PSNR和SSIM比其他算法高,PSNR大約高1～2dB.從視覺上也可以看出,本文算法對細節的重建較為突出,是較為理想的SR重建算法.

表2 各種算法字典訓練時間的比較(min)Table 2 Comparison of various algorithm dictionary training times(min)

為了證明所提方法的效率,對字典訓練所花費的時間進行了驗證.本實驗與Yang′s、Fu′s、CFS算法進行了比較,表2記錄了各算法在字典訓練階段所消耗的時間.可以明顯看出,本算法在一定程度上減少了運行時間.

6 結 論

針對目前算法重建圖像細節處理不足的現象,本文提出了一種基于自適應匹配追蹤的稀疏表示超分辨率重建算法,大大提高重建的效果.將大量的訓練集通過K-SVD算法進行字典訓練,訓練得到高、低分辨率字典,然后利用訓練得到的字典將輸入的低分辨率圖像進行超分辨率重建,使用自適應匹配追蹤算法進行稀疏編碼.實驗結果表明,與基于OMP的各種算法相比,不論在客觀上還是主觀上,本文算法都達到了不錯的重建效果,特別在細節方面,重建效果更為理想.同時,字典訓練的時間也明顯優于其他算法.因此,本文算法在精度和效率上都有明顯的提升.但是,隨著放大尺度的增加,算法的性能有所降低,下一步的研究將會集中在這一方面.