核協同近鄰表示的人臉識別算法

李昆侖，李尚然，王 琳，鞏春景

(河北大學 電子信息工程學院，河北 保定 071000)

1 引 言

人臉識別作為一種代表性的模式識別問題[1]，近幾年在計算機視覺領域中受到了廣泛關注，并且已應用到了諸多領域，例如基于人臉識別的門禁系統、視頻監控[2]、行人追蹤[3]等.

稀疏表示分類(Sparse Representation based Classification，SRC)[4]算法利用所有訓練樣本形成過完備字典，通過字典中少量元素的線性組合表示測試樣本，最后利用這種稀疏的線性組合完成分類任務.但在尋找最佳線性組合時，稀疏表示分類(SRC)需要線性組合的系數滿足L1-范數最小化的約束條件.文獻[5]指出在表示未知樣本時，訓練樣本的類間協同性有著更重要的作用，即實際改善人臉識別效果的并不是稀疏表示，而是協同表示，并且提出了協同表示分類(Collaborative Represention based Classification，CRC)算法.協同表示分類(CRC)利用L2-范數最小二乘法求解表示系數，不僅達到了與稀疏表示分類(SRC)近似的識別效果，而且還降低了時間復雜度.文獻[6]在最近子空間(Nearest Subspace，NS)分類器中加入吉洪諾夫正則項，隨后與協同表示分類(CRC)結合，提出最近正則子空間(Nearest Regularized Subspace，NRS)分類器.為了強化最近正則子空間(NRS)的分類能力，文獻[6]又將樣本投影到局部Fisher判別分析(Local Fisher Discriminant Analysis，LFDA)[7]的局部投影空間中，在局部投影空間中構造吉洪諾夫正則矩陣.文獻[8]將協同表示分類(CRC)與局部線性嵌入(Locally Linear Embedding，LLE)[9]結合，提出協同近鄰表示分類(Collaborative Neighbor Representation based Classification，CNRC)算法.協同近鄰表示分類(CNRC)利用歐式距離作為度量準則，在訓練樣本中自動地選擇最近鄰點作為表示基，將選擇的表示基和所有訓練樣本結合，利用正則最小二乘法求解線性表示系數，最后通過表示系數線性地重構未知樣本，進一步強化表示能力，改善識別效果.

協同近鄰表示分類(CNRC)利用樣本間的相似性表示人臉特征，由于忽略了因相似性造成的非線性性，使得它主要面臨以下兩個問題：

1)在輸入空間中利用歐式距離尋找未知樣本的最近鄰點，選擇的表示基很難準確表示測試樣本，導致識別誤差增大；

2)由于忽略了樣本間的非線性關系，使得協同近鄰表示分類(CNRC)很難利用樣本的非線性特征向量，從而限制了它的分類性能.

在解決非線性問題時，最常用的方法是引入核方法.核方法有諸多特點：

1)核方法定義的非線性映射將輸入空間的數據投影到高維甚至是無限維的核空間[10]，在一定程度上使輸入空間中非線性可分的特征向量在投影到核空間后線性可分；

2)通過核方法的非線性映射，可以改變樣本的分布，更容易聚集同類樣本，并可達到分類間隔的最大化；

3)由于核方法是基于VC維理論的，因而具有優秀的泛化能力.考慮到核方法在解決非線性問題時的優勢，文獻[11]將輸入空間的樣本投影到核空間，在核空間中構造稀疏表示分類(SRC)算法，提出基于核方法的稀疏表示分類(Kernel based Sparse Representation Classification，KSRC)算法.由于引入核方法必定會增加算法的時間復雜度，并且核稀疏表示分類(KSRC)仍需要求解L1-范數的最小化問題，文獻[12]將樣本投影到核空間后，利用協同表示分類(CRC)的正則最小二乘法構造表示框架，在核空間中嵌入協同表示分類(CRC)，提出核協同表示分類(Kernel Collaborative Representation Classification，KCRC)算法.文獻[7]在局部Fisher判別分析(LFDA)的降維過程中進一步考慮到非線性問題，利用核方法構造局部Fisher判別分析(LFDA)，提出核局部Fisher判別分析(Kernel Local Fisher Discriminant Analysis，KLFDA)算法.

針對協同近鄰表示分類(CNRC)忽略了樣本間非線性關系的問題，本文利用核函數能改變樣本空間分布的性質，對協同近鄰表示分類(CNRC)進行兩點改進：

1)利用核局部Fisher判別分析(KLFDA)的核局部投影空間定義度量準則distKLFDA，提出基于核局部投影度量的協同近鄰表示分類算法(CNRC_KLFDA).CNRC_KLFDA利用distKLFDA將樣本向量投影到核局部投影空間中，改變樣本的空間分布，在增大類間離散度和減小類內離散度的同時，使得協同近鄰表示分類(CNRC)在尋找最近鄰表示基時能利用一定程度的非線性關系，改善識別效果.

2)引入適當的核函數，將所有樣本投影到核空間，在核空間中利用核近鄰[13]算法尋找未知樣本的最佳表示基，提出基于核方法的協同近鄰表示分類(Kernel based Collaborative Neighbor Representation based Classification，KCNRC)算法，核協同近鄰表示分類(KCNRC)不僅能強化訓練樣本的表示能力，而且通過核方法的非線性映射，在一定程度上使一些線性不可分的樣本特征向量在核空間中線性可分，能進一步提高識別性能.

2 核方法和核局部Fisher判別分析

2.1 核方法

文獻[14]指出，利用核方法的非線性映射，幾乎所有的線性方法都可以找到對應的非線性方法.假設非線性映射為φ，φ將原始空間m中的樣本x投影到核空間H中：

m→H，x→φ(x)

(1)

通常情況下，由于我們不知道非線性映射φ的具體形式，樣本數據通過核方法投影到核空間后是無法計算的.但是利用核函數，使數據在核空間中的內積可以通過核函數求得[25]，這樣既使在不知道映射函數具體表達式的情況下，依然可以得到數據在核空間的解，即：

k(x，y)=〈φ(x)，φ(y)〉

(2)

這里〈φ(x)，φ(y)〉為φ(x)和φ(y)在高維空間的內積，k(x，y)是x和y的核函數.

2.2 協同近鄰表示分類(CNRC)

定義D=[D1，D2，…，Dc]∈m×n為所有樣本組成的訓練集，Di=[di，1，di，2，…，di，ni]∈m×ni表示第i類訓練樣本，這里i=1，2，…，c，n1+n2+…+nc=n，其中Di中的每個列向量表示一個樣本，共c類.CNRC從訓練樣本中尋找最佳的表示基，這些表示基張成的線性子空間和未知樣本y∈m×1所在的子空間近似相等，且它們能線性地重構y，最后利用最小二乘法構造協同近鄰表示函數：

(3)

求解式(3)可得：

x=(DTD+λI+σDNH)-1DTy

(4)

2.3 核局部Fisher判別分析

(5)

(6)

式(5)和式(6)中的Ai，j∈[0，1]為n維的度量矩陣，Ai，j表示A的第個(i，j)元素，di與dj的距離越小，對應的Ai，j越大，一般采用歐式距離作為度量方法.給定核函數k(x，y)，核局部投影空間定義為求解廣義特征值問題：

KL(m)Kφ=λKL(w)Kφ

(7)

Ki，j=〈φ(di)，φ(dj)〉=k(di，dj)

(8)

令式(7)解得的特征值λ1≥λ2≥…≥λr，則前P≤r個特征值所對應的特征向量構成核局部投影空間TKLFDA=(φ1，φ2，…，φp)∈m×p.

3 基于核方法的協同近鄰表示分類框架

3.1 基于核局部投影度量的協同近鄰表示分類算法(CNRC_KLFDA)

給定屬于第i類的測試樣本y，CNRC認為在局部流形域內的近鄰樣本，比流形域外的其它樣本能更好的表示y，所以在尋找表示系數的過程中，CNRC利用歐式距離優先選擇y的最近鄰點作為表示基.

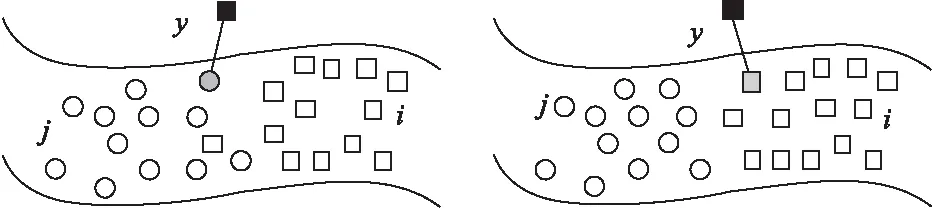
圖1 CNRC表示基選擇Fig.1 Representation bases selection of CNRC圖2 核局部投影度量示意圖Fig.2 Diagram of kernel local projection metric

由于一些特征向量在輸入空間中存在著非線性關系，歐式距離很難準確選擇未知樣本的最佳表示基，如圖1所示，小圓表示第j類，方塊表示第i類，黑色實心方塊表示y，灰色實心圓表示利用歐式距離選擇的最近鄰表示基，而在輸入空間中利用歐式距離選擇的最近鄰表示基屬于第j類，此時利用它和所有訓練樣本重構y，會使y與第j類最相似，最終導致誤分類.KLFDA在確保樣本類內散度最小，類間散度最大的基礎上引入核方法，生成核局部投影空間，通過核局部投影空間的投影后，一部分線性不可分特征向量變得線性可分.本文利用KLFDA的核局部投影空間對輸入樣本進行非線性投影，定義非線性度量準則：

(9)

經過TKLFDA投影后，投影樣本的空間分布被改變，樣本類間距離增大，類內間距減小，如圖2所示，此時利用distKLFDA所選擇的最近鄰表示基屬于第i類，所以重構的樣本與第i類最相似，這樣便使得識別性能改善.

針對CNRC在尋找最佳表示基時無法利用樣本間非線性特征向量的問題，本文在KLFDA的核投影空間中尋找能夠表示未知樣本的最佳近鄰點，提出基于核局部投影度量的協同近鄰表示分類(CNRC_KLFDA)算法.如圖2所示，在KLFDA的核投影空間中通過非線性映射使得同類樣本更容易聚集，在此基礎上CNRC_KLFDA利用式(9)定義的非線性度量準則distKLFDA選擇能夠更加準確重構y的表示基，從而提高識別率.CNRC_KLFDA在CRC的框架中利用distKLFDA選擇表示基，為了使距離y越近的表示基獲得的權值越大，同時使得求解的表示系數中距離y越近的表示基系數權值越大，本文定義CNRC_KLFDA的目標函數為：

(10)

(11)

此時，

(12)

求得x后，可得每類樣本的重殘差：

(13)

CNRC_KLFDA算法描述如下：

算法1.CNRC_KLFDA

輸入：字典D，未知樣本y，平衡參數σ>0和λ>0，核函數k(x，y).

1.字典和未知樣本歸一化.

2.利用式(7)解得核局部投影空間TKLFDA.

3.通過式(9)，(11)，(12)求解表示系數.

4.通過式(13)計算各類重構殘差ri(i=1，2，…，c).

輸出：y所屬類別，identity(y)=argminiri(y).

3.2 基于核方法的協同近鄰表示分類算法

CNRC_KLFDA在尋找最近鄰表示基時，通過核局部投影空間改變樣本的空間分布，利用distKLFDA尋找y的最近鄰表示基完成識別任務.本文提出第二種改進方法，將所有樣本投影到核空間，在核空間中嵌入CNRC，提出基于核方法的協同近鄰表示分類 (KCNRC)算法.首先，KCNRC利用非線性映射φ，將所有樣本投影到核空間H：

Di∈m→Φi∈H
D∈m→Φ∈H
y∈m→φ(y)∈H

(14)

公式(14)中Φ=[Φ1，Φ2，…，Φc]=[φ(D1)，φ(D2)，…，φ(Dc)]為訓練集在核空間的表達形式，第i類的訓練集為Φi=[φ(di)，φ(di)，…，φ(di)]，i=1，2，…，c，φ(y)代表核空間中的未知樣本.核空間中樣本φ(x)和φ(y)之間距離的平方為：

d2(φ(x)，φ(y))=k(x，x)-2k(x，y)+k(y，y)

(15)

則，定義KCNRC的目標函數為：

(16)

求解公式(16)可得：

x=(ΦTΦ+λI+σΓTΓ)-1ΦTφ(y)

(17)

是公式(17)中ΓTΓ表示在核空間中和φ(y)每個訓練樣本的距離所組成的對角矩陣：

(18)

(19)

為了進一步減小計算復雜度，本文引入定理1，重新定義殘差函數：

(20)

證明：

令

(21)

則式(19)的殘差方程可重新定義：

(22)

(23)

顯然，公式(20)在核空間中可以利用核函數求得，最終將未知樣本y分到殘差最小的類別中.KCNRC算法的具體識別步驟如算法2.

算法2.KCNRC

輸入：字典D，未知樣本y，平衡參數σ>0和λ>0，核函數k(x，y).

1. 字典和未知樣本歸一化.

2. 通過式(15)，(17)，(18)求解表示系數.

3. 通過式(20)計算各類重構殘差ri(i=1，2，…，c).

輸出：y所屬類別，identity(y)=argminiri(y).

4 實驗結果與分析

為了驗證CNRC_KLFDA和KCNRC算法對光照、姿態、面部表情變化的魯棒性，用ORL人臉庫、AR人臉庫[15]、Extended Yale B人臉庫[16]3個不同的人臉數據庫驗證它們的有效性.對于核函數的選擇，本文對提出的兩種算法都采用高斯核函數k(x，y)=exp(-‖x-y‖2/t).所有的實驗在CPU為i5-4200U，2.30GHZ，內存為4G的計算機上運行，實驗軟件為MATLAB- 2016a.

4.1 人臉庫

ORL人臉庫包括40類，每類10副圖像，圖像大小為92×112，包括姿態和面部表情變化，部分人臉圖像如圖3所示.

AR人臉庫包括4000副圖像，共126人，每幅圖像的大小為120×165，包括面部表情變化，光照變化和人臉遮掩圖像.我們采用文獻[4]和文獻[5]的實驗方法，選取人臉庫的一個子集，這個子集包括光照變化和面部表情變化，由50名男性和50名女性組成，每人14副圖像.部分人臉圖像如圖4所示.

圖3 ORL數據庫中的部分人臉圖像Fig.3 Part of the face image on ORL database

圖4 AR數據庫中的部分人臉圖像Fig.4 Part of the face image on AR database

Extended Yale B 由38個人的2414副人臉圖像組成，每人64副圖像，該數據庫為光照變化數據庫，且光照變化范圍較廣，主要用來驗證算法對光照的魯棒性，部分人臉圖像如圖5所示.

圖5 Extended Yale B數據庫中的部分人臉圖像Fig.5 Part of the face image on Extended Yale B database

4.2 參數設置

合適的參數可以讓實驗結果達到更好的效果，此部分采用PCA[17]提取圖像特征.

1)ORL數據庫：隨機選取每類的5副圖像共200副作為訓練集，剩下的為測試集，人臉圖像降到80維，取0<σ<1，0<λ<1，采用格點搜索法，改變一個參數，固定剩下的參數.核函數的參數設置采用整體到局部的搜索策略，t的搜索為范圍從1到15，每個參數的改變都取20次實驗的最大平均識別率，表1為ORL人臉庫上最佳參數和對應的識別率.

表1 ORL人臉庫上的最佳參數和對應的識別率Table 1 Best parameters and the corresponding recognition rate on ORL face database

2)AR人臉庫：每次實驗都隨機選取每人的7副圖像作為訓練集，剩下的為測試集.將所有樣本降維到300維進行參數設置，t的搜索為范圍從1到20，每次改變參數都重復20次實驗，表2為AR人臉庫中最佳參數和對應的最大平均識別率.

表2 AR人臉庫上的最佳參數和對應的識別率Table 2 Best parameters and the corresponding recognition rate on AR face database

3)Extended Yale B數據庫：隨機選取每類的32副圖像作為訓練集，剩下的為測試集，將所有樣本降維到500維進行參數設置，t的搜索為范圍從1到25，每次改變參數都重復20次實驗，表3為Extended Yale B人臉庫上最佳參數和對應的最大平均識別率.

表3 Extended Yale B人臉庫上的最佳參數和對應的識別率Table 3 Best parameters and the corresponding recognition rate on Extended Yale B face database

4.3 特征向量維數對識別效果的影響

特征向量維數的大小將直接影響算法的識別效果，特征向量維數越大，保留原圖像的特征信息也就越多，識別的效果也就越好.為了驗證本文所提算法的識別效果，訓練樣本的選擇方式與4.2節一樣，對比的算法有KSRC，KCRC，CNRC.算法的參數采用4.2節的最佳參數，最終取20次實驗的平均識別率，實驗結果如圖6～圖8所示，對比實驗結果可以發現：

圖6 ORL數據庫中不同特征向量維數和對應的識別率Fig.6 Different feature dimension and corresponding recognition rate in ORLdatabase

圖7 AR數據庫中不同特征向量維數和對應的識別率Fig.7 Different feature dimension and corresponding recognition rate in AR database

1)在CNRC中引入核方法后，能到達更好的識別效率，特別是在低維時，比如在ORL數據庫中，當人臉特征為10維時，CNRC_KLFDA和KCNRC比CNRC的識別率要高10%～15%，這是由于在低維時，樣本間線性不可分的特征較多，此時能充分發揮核方法的優勢，將一部分線性不可分的特征變得線性可分，能明顯改善識別效果.

圖8 Extended Yale B數據庫中不同特征向量維數和對應的識別率Fig.8 Different feature dimension and corresponding recognition rate in Extended Yale B database

2)當特征向量維數較低時，CNRC_KLFDA和KCNRC比CNRC都有較高的識別率，但隨著特征維數的增加，CNRC_KLFDA的識別效果與KSRC和KCRC基本相同.而KCNRC并沒有這種局限性，因為它將所有樣本投影到核空間，在核空間中樣本的分布被改變，樣本類內距離減小，類間距離增大，所以將原始算法嵌入到核空間后能達到更好的識別效果.從實驗結果中也可以看出，KCNRC的識別率要比CNRC_KLFDA高出1%～2%.

5 總 結

核方法在解決模式識別的非線性問題時所表現的高效性，使得很多算法在引入核方法后能取得更好的效果.在人臉識別任務中CNRC屬于線性算法，無法利用人臉圖像的非線性關系，針對此問題，本文引入核方法，提出兩種改進算法：

1)在CNRC選擇最佳表示基時，在KLFDA的核局部投影空間中定義新的度量方法distKLFDA代替輸入空間中的歐式距離，distKLFDA在核局部投影空間中度量樣本特征向量之間的距離，尋找能表示未知樣本的最佳表示基.

2)將所有樣本投影到核空間，將CNRC嵌入到核空間中，一定程度上解決了原始算法的非線性問題，提高識別效果.最終的實驗結果證明了本文所提算法對人臉的光照，姿態，表情變化的魯棒性.

CNRC_KLFDA僅僅在核局部投影空間中選擇樣本的最佳表示基，只是利用到樣本的局部非線性特征，很難達到更高的識別效果.KCNRC雖然能進一步利用到所有樣本的非線性特征，改善識別效果，但由于引入了核方法，并且需要設置較多的參數，當訓練樣本增加時，會進一步增加算法的時間復雜度.受字典學習[18-20]的啟發，本文的下一步工作是對訓練樣本進行學習，去除訓練樣本中的冗余元素，使在增加訓練樣本的情況下，盡可能地減小計算復雜度.