結合分數階微分與結構張量的醫學圖像細微結構增強

王 宇，王遠軍，靳珍怡，方麗萍

1(上海理工大學 醫療器械與食品學院，上海 200093)

2(復旦大學 附屬中山醫院，上海 200032)

3(上海市影像醫學研究所，上海 200032)

1 引 言

醫學圖像增強主要分為對比度增強和細微結構增強，常用的對比度增強算法有對數或指數變換、灰度拉伸線性變換、直方圖均衡化和Retinex算法等.但是對比度增強只能改善圖像的灰階層次，而圖像的紋理細節沒有得到改善，這會影響到醫生對病灶細節的判讀和診斷，所以研究醫學圖像細微結構的增強具有重要的臨床意義[1].目前常用的醫學圖像紋理結構細節增強方法根據不同增強方法原理特點，主要可以分為銳化增強、粗糙集模糊集增強[2，3]、多尺度幾何增強[4]以及基于微分算子的增強方法[5-7]等.針對不同的醫學圖像成像特點，各種方法既有其優勢也有其缺點，例如銳化增強可以增強圖像的小細節以及邊緣部分，但是對噪聲比較敏感；模糊集增強雖然可以處理醫學圖像中大量的不確定性，得到較好的增強效果，但是需要依賴較多先驗知識，魯棒性低；多尺度幾何增強可以從多個尺度對圖像進行有針對性的增強，但容易產生“振鈴”效應；基于微分算子的增強可以有效處理角點、管狀等結構，但是Hessian矩陣的特征值與特征向量計算量大，影響處理效率.所以本文在這些方法的基礎上，綜合其優點，選取分數階微分與結構張量相結合，希望可以對醫學圖像增強具有一般適用性，實現更優的細微結構增強效果.

結構張量首先被提出主要是用于數字圖像處理，現已被廣泛應用于圖像增強[6，7]、分割[8]、融合[9，10]以及重建[11]等方面.結構張量是基于圖像的梯度信息構建的一階矩陣，結合圖像的局部信息，可以獲得比梯度特征更多的圖像局部幾何結構信息，即更好地描述圖像的邊緣、形狀、角點等紋理結構信息[9，12].結構張量可以反映圖像鄰域內的像素變化特性，并且是由張量濾波后得到，因此結構張量對噪聲具有更強的魯棒性，可以提取出圖像的穩定結構特征，有利于增強圖像的紋理細節[13].盡管George[6]以及Moreno等人[7]結合擴散濾波使用結構張量可以有效增強醫學圖像中的管狀結構，但是這些方法大多都是結合擴散方程以針對血管這種管狀結構進行增強，而對分形樣紋理以及邊緣細節等特征沒有詳細描述.

傳統的微分算子如Sobel算子、Prewitt算子是一階邊緣銳化算子，可沿水平方向和垂直方向銳化圖像的邊緣，Laplacian算子是二階邊緣銳化算子，對噪聲比較敏感.這些算子都是整數階微分運算，可以增強圖像的高頻邊緣輪廓信息，但對圖像紋理細節增強效果甚微.分數階微分算子是整數階微分運算的推廣，研究發現，分數階微分算子比整數階微分算子更有利于分析和強化圖像紋理細節信息[14，15].

結合上述結構張量與分數階微分算子對圖像紋理細節處理的優點，本文嘗試將分數階微分算子與結構張量相結合，構建基于分數階微分算子的結構張量，從結構張量的特征值和特征向量可以研究所構建的分數階局部圖像描述算子對區分圖像紋理不同結構區域特征的特性，從低頻信號分數階微分不為零的特點可以研究其對圖像紋理的弱結構、小尺度以及結構信息的保持特性，在此基礎上提出了結合分數階微分算子與結構張量的醫學圖像細微結構增強的方法.在實驗中，我們選取了包括計算機斷層掃描(Computed Tomography，CT)和磁共振(Magnetic Resonance Imaging，MR)在內的多種模態的典型醫學圖像做了對比增強實驗，并對實驗結果分別進行定性和定量評價，結果表明本文提出的方法可以有效地增強圖像的紋理細節，并能較好地保留圖像的平滑區域以及弱紋理區域，具有良好的視覺效果，驗證了該方法的有效性.

2 理論介紹

2.1 結構張量

定義二維圖像I(x，y)：Ω→R2，I(x，y)表示點(x，y)處的灰度值，點(x，y)的梯度向量為▽I=(Ix，Iy)T，則輸入圖像的梯度可以在歐幾里得空間RT進行說明[13]：

(1)

dI的平方范數可以表示成：

=(dxdy)G(dx

dy)

(2)

其中G的表達式為：

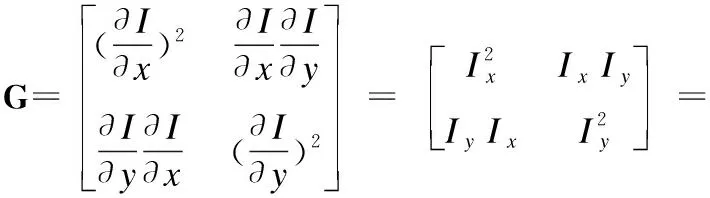
(3)

G即表示張量，T表示向量轉置.通過公式(3)可以看出矩陣G是一個對稱半正定矩陣，為了使其包含局部結構信息，通過濾波技術對張量場進行平滑，經過濾波平滑后的張量即為結構張量，表達式為：

(4)

gσ為方差是σ的高斯函數，*為卷積運算.矩陣的特征向量e1、e2表示該鄰域內信號變化的方向，其非負特征值λ1、λ2表示沿這些方向變化的大小信息，可以反映圖像的結構信息[16]：①若λ1≈λ2≈0，則表示圖像在該點附近任何方向灰度變化幾乎為0，可以認為是圖像的平滑區域；②若λ1≈λ2>>0，則表明圖像在該點無論是水平方向還是垂直方向變化率都很大，可以認為是圖像的角點部分；③若λ1>>λ2≈0，則表示圖像在該點附近的水平變化率要遠遠大于垂直變化率，可以認為是圖像的邊緣區域或流線區域.

根據特征值之間的關系可以進一步給出局部像素灰度值之間的相干性度量(Coherence)[17]來描述圖像的局部信息，同時為了突出圖像的紋理細節部分以及邊緣區域，使之具有更好的結構表達能力，相干性度量Coh定義如下：

(5)

2.2 分數階微分算子

分數階微分增強圖像主要是通過構建分數階微分掩模算子，計算像素點及其鄰域像素點關系的濾波增強.首先根據圖像應用中最廣泛應用的Grünwald-Letnikov(G-L)定義[18]，可推導出一維信號的分數階差分表達式，然后在一維的基礎上可推導出二維信號的分數階差分表達式.

假設一維信號f(t)的持續時間為t∈[a，b]，通過取單位間隔h=1可將信號分成相等間隔，即m=[(b-a)/h]=[b-a]，則一維信號f(t)的α階微分差分表達式為：

(6)

對于二維信號f(x，y)，因為像素點的最小間隔為1，根據公式(6)可以推導出f(x，y)在x和y方向的分數階偏微分近似表達式：

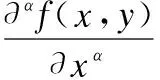
(7)

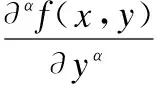
(8)

其中Γ(n)為Gamma函數，其定義為：

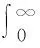
(9)

根據二維信號的分數階表達式，可以發現分數階微分要比整數階微分連續性更好，對圖像來說，紋理細節表達能力也要更好，連續性更強.根據不同方向上的系數取決于與中心像素點之間距離的關系，由此構建的八方向各向同性分數階Tiansi 微分算子掩模模板如圖1所示[15].在圖像掩模計算時，對模板要進行歸一化處理，對各項同時除以(8-12α+4α2).

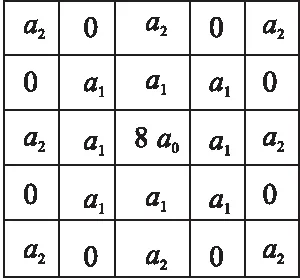
圖1 Tiansi 微分算子模板Fig.1 Tiansi differential operator template

其中，a0，a1，a2分別定義如下：

(10)

2.3 基于分數階微分算子的結構張量

由于紋理細節區域的整數階微分值可能幾乎接近零，而分數階微分在處理圖像紋理細節時，比整數階更加精準.因此，將分數階微分引入結構張量能更精確描述分形樣紋理和邊緣細節的特征，使之更加清晰連續.根據上述分析，α階分數階結構張量可以定義為：

(11)

為了盡量減小誤差又不使運算量過大，選取公式(7)(8)中的前三項做差分運算，所以：

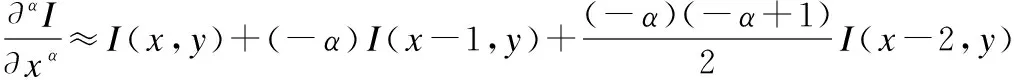
(12)

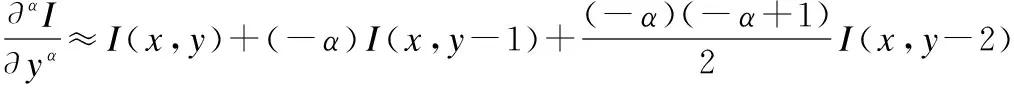
(13)

3 實驗結果與討論

由于圖像的細微結構主要是圖像的高頻信息，根據小波變換可將圖像分為近似信息的低頻部分以及包含細節的高頻部分，本文將結合小波變換實現具體算法.對圖像來說，利用小波分解后得到的低頻信息主要是圖像變化緩慢的區域，即圖像主要輪廓部分[19]，我們可利用Tiansi微分掩膜算子對低頻信號進行處理，加強圖像輪廓的提取；分解后得到的高頻信息主要是圖像變化迅速的區域，反應圖像的細節信息，主要分為水平、垂直和對角線三個細節子帶，利用分數階結構張量可以描述更豐富的局部細節信息，然后可根據加權各高頻分量得到具有更清晰連續的紋理細節的高頻信號.根據上述分析，整個實驗的算法流程圖如圖2所示.

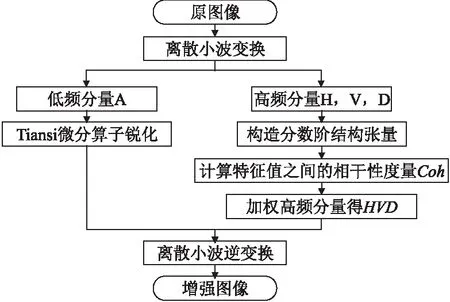
圖2 算法具體流程圖Fig.2 Detailed algorithm flow chart

流程圖中H，V，D分別代表小波分解后水平、垂直和斜對角方向的高頻分量；Coh表示高頻分量的相干性度量，是根據高頻分量的分數階結構張量的特征值構造而成，三個高頻分量的相干性度量分別為CohH，CohV，CohD；HVD表示為加權各高頻分量后得到的最后高頻分量，具體定義為：

(14)

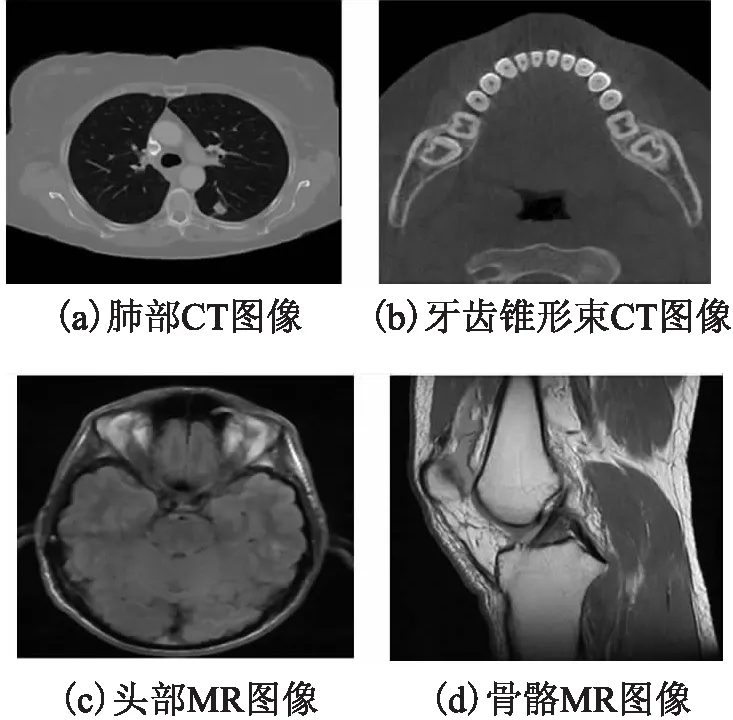
圖3 實驗原圖Fig.3 Experiment original images

為驗證算法的自適應性，我們選取了不同模態不同解剖部位的醫學圖像作為增強實驗的原圖像，具體如圖3所示，其中(a)是肺部CT圖像，(b)是牙齒錐形束CT圖像，(c)是頭部MR圖像，(d)是骨骼MR圖像.我們以MATLAB2016b為平臺進行算法驗證，選取結構張量增強、整數階微分算子(Sobel微分算子)增強、分數階微分算子(Tiansi算子)增強[15]、以及自適應分數階增強[20]作為對比實驗，結構張量增強方法主要是對高頻分量構造的結構張量，然后再根據相干性度量加權，低頻部分不做任何處理.實驗中用到的分數階次均選取α=0.6.具體實驗結果如圖4-圖7所示.

圖4是肺部CT圖像的增強效果對比圖，其中(a)是實驗原圖，(b)是本文方法得到的增強實驗結果圖，(c)表示的是結構張量方法得到的增強實驗結果圖，(d)表示的是整數階Sobel微分算子增強方法得到的增強實驗結果圖，(e)表示的是文獻[15]中分數階Tiansi微分算子增強方法得到的增強實驗結果圖，(f)表示的是文獻[20]中自適應分數階增強方法得到的增強實驗結果圖.對比各實驗結果圖可以發現，特別是針對圖(a)中標出的感興趣區域，(b)圖中的肺部血管增強較為明顯，且病灶的邊緣輪廓也有所增強，圖像更加清晰；(d)圖和(e)圖中，血管的清晰度也有所相應的增強，但整體視覺效果不如(b)圖；而(f)圖中，文獻[20]方法出現了較為嚴重的失真現象.

圖4 肺部CT圖像增強效果對比Fig.4 Effect contrast of lung CT image enhancement

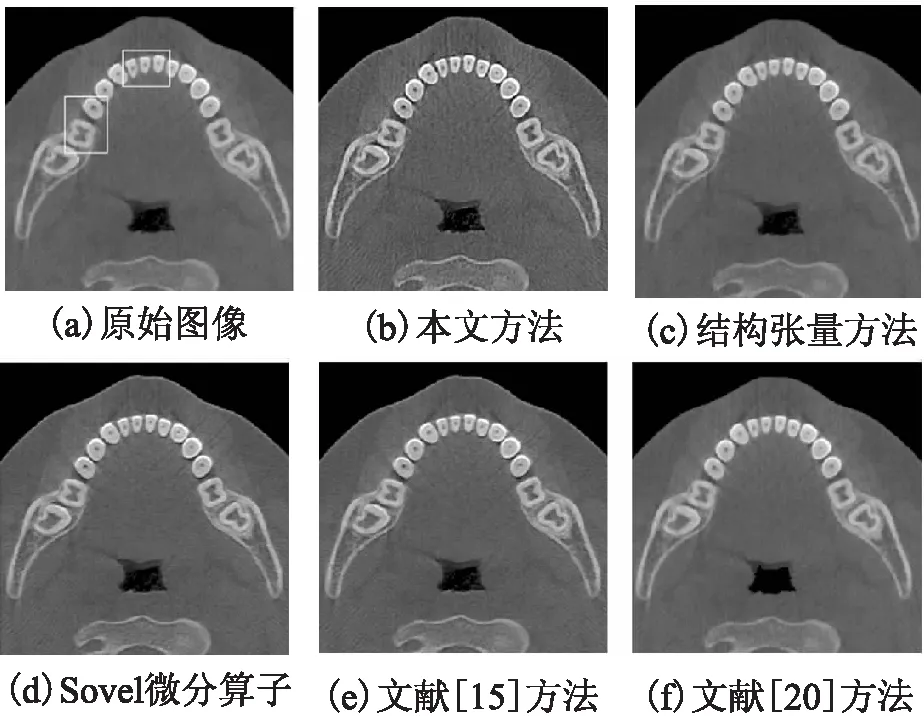
圖5 牙齒錐形束CT圖像增強效果對比Fig.5 Effect contrast of tooth cone beam CT image enhancement

圖5是牙齒錐形束CT圖像的增強效果對比圖，其中(a)是實驗原圖，(b)是本文方法得到的增強實驗結果圖，(c)表示的是結構張量方法得到的增強實驗結果圖，(d)表示的是整數階Sobel微分算子增強方法得到的增強實驗結果圖，(e)表示的是文獻[15]中分數階Tiansi微分算子增強方法得到的增強實驗結果圖，(f)表示的是文獻[20]中自適應分數階增強方法得到的增強實驗結果圖.對比各實驗結果圖可以發現，相對(a)圖中感興趣區域中的切牙、前磨牙和磨牙部分，(b)圖中牙齒的邊緣輪廓相比更為清晰，有利于進一步的分割等后續處理；(f)圖雖然增強效果不明顯，但是有效的去除了噪聲，具有良好的去噪效果.

圖6是頭部MR圖像的增強效果對比圖，其中(a)是實驗原圖，(b)是本文方法得到的增強實驗結果圖，(c)表示的是結構張量方法得到的增強實驗結果圖，(d)表示的是整數階Sobel微分算子增強方法得到的增強實驗結果圖，(e)表示的是文獻[15]中分數階Tiansi微分算子增強方法得到的增強實驗結果圖，(f)表示的是文獻[20]中自適應分數階增強方法得到的增強實驗結果圖.從圖6(b)可以看出，本文方法對頭部MR圖像有增強效果但不如之前CT圖像增強效果明顯，主要是因為頭部MR圖像的高頻信號相對較少，所以此方法得到的圖像增強效果不太明顯.

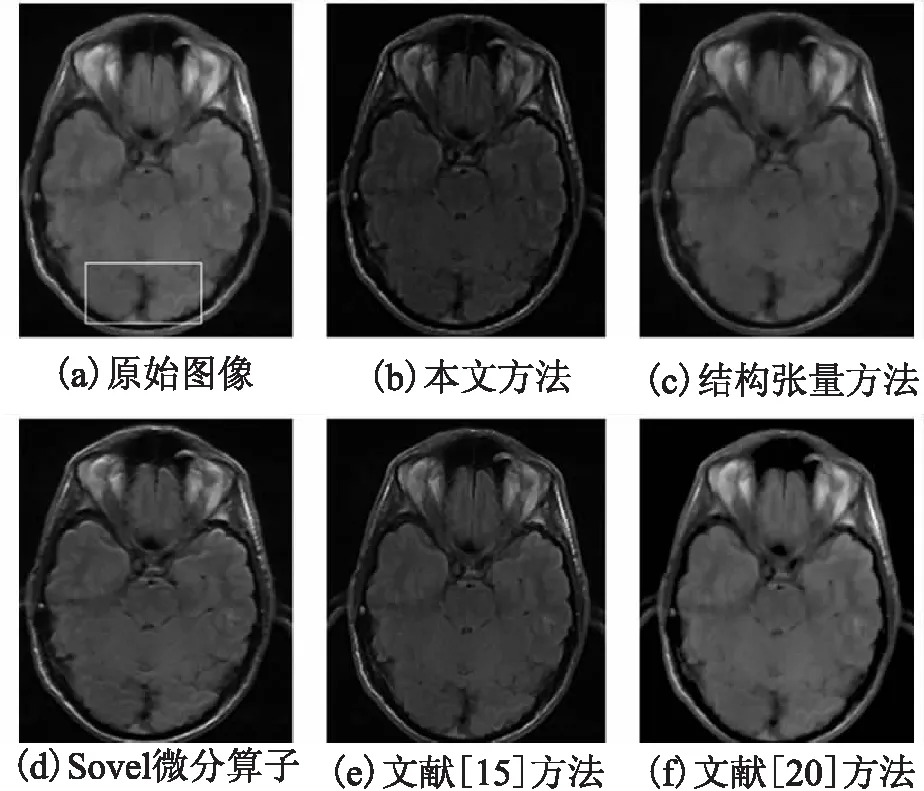
圖6 頭部MR圖像增強效果對比Fig.6 Effect contrast of head MR image enhancement

圖7是骨骼MR圖像的增強效果對比圖，其中(a)是實驗原圖，(b)是本文方法得到的增強實驗結果圖，(c)表示的是結構張量方法得到的增強實驗結果圖，(d)表示的是整數階Sobel微分算子增強方法得到的增強實驗結果圖，(e)表示的是文獻[15]中分數階Tiansi微分算子增強方法得到的增強實驗結果圖，(f)表示的是文獻[20]中自適應分數階增強方法得到的增強實驗結果圖.從圖7中可以看出，針對(a)圖中標出的感興趣區域，(b)圖中肌肉紋理以及與骨頭連接處韌帶的紋理細節相比其他圖像增強效果更加明顯，圖像的細微結構更加清晰，圖(c)(d)(e)相比較原圖也有增強效果，其中(d)圖主要是增強了圖像的邊緣輪廓.(b)(d)(e)圖中都不可避免的增強了噪聲，而(f)圖中對噪聲的魯棒性較強.

對圖4-圖7總體對比發現，本文方法的增強效果在圖4(b)、圖5(b)和圖7(b)中表現較明顯，說明本文提出的結合分數階微分算子與結構張量的增強方法在增強圖像輪廓邊緣的同時可以有效的增強圖像細微結構，具有良好的視覺效果；從圖4(d)-圖7(d)和4(e)-圖7(e)之間對比可以看出，Sobel算子雖然和Tiansi分數階算子均可以不同程度的增強圖像的細節，但是Sobel算子增強圖像主要是銳化圖像邊緣輪廓，其中以圖5(d)、圖6(d)較為明顯，而Tiansi 分數階算子則主要側重于增強圖像的紋理細節部分，其中以圖4 (e)和圖7 (e)較為明顯，說明分數階微分算子在紋理細節增強上要優于整數階微分算子.

為了進一步說明本文方法的有效性，將信息熵(Entropy)，平均梯度(Meangradient)以及對比度改善指數(Contrast Improvement Index，CII)作為圖像紋理細節增強定量評價指標，結果如表1-表4所示.其中信息熵，平均梯度以及CII定義如下：

1)信息熵是衡量圖像信息豐富程度的一個重要指標.圖像的信息熵越大，則圖像中包含的信息量越豐富，圖像的邊緣和紋理細節越明顯.圖像熵的定義為：

H(p)=-∑p(i，j)logp(i，j)

(15)

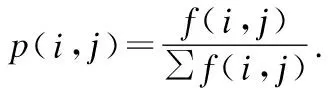
2)平均梯度又稱為清晰度，反映了圖像中的微小細節反差與紋理變化特征，同時也反映了圖像的清晰度.其定義為：

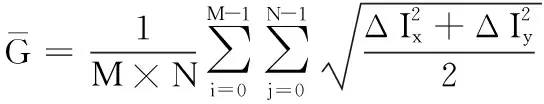
(16)

式中ΔIx與ΔIy分別為x，y方向上的差分.

3)CII用來衡量圖像的整體對比度，反映圖像整體和細節的增強效果.CII值大于1，表明有增強效果，值越大，表明圖像細節信息增強越明顯，且具有良好的視覺效果.其定義如下[21]：

(17)

Cproposed和Coriginal分別為增強后圖像和原圖像的局部對比度.C定義為：

(18)

分析表1-表4中數據可以看到，本文提出的方法在平均梯度參數值上約是原圖的2倍，說明本文方法有效增強了圖像中的紋理細節部分，增強了圖像的清晰度；同時可根據信息熵參數發現，本文方法對應增強圖像的信息熵也有相應的增加，可以說明該方法豐富了圖像信息，有效的保留了圖像平滑區域以及弱紋理區域；另外從對比度改善指數也可以發現，本文提出的方法CII值是對比方法中最高的，說明本文方法增強的圖像具有良好的視覺效果.從這三個指標可以總結出，結合分數階與結構張量增強的圖像具有分數階增強以及結構張量增強兩方面的優勢，相比較單一的分數階增強方法而言，分數階結構張量增強的圖像噪聲比較小，圖像信息豐富程度也較高；而相比較單一的結構張量增強方法，分數階結構張量可以更加清晰的表達圖像紋理細節.整體實驗說明本文提出的方法可以有效的增強圖像的紋理細節，并能較好的保留圖像的平滑區域以及弱紋理區域，具有良好的視覺效果.盡管在表3和表4中，針對MR圖像，文獻[20]方法增強圖像得到的信息熵值較為突出，主要是文獻[20]方法具有良好的去噪效果，但圖像的平均梯度值以及CII值都相比較低，圖像的清晰度不夠好.再者，從視覺評價上結構張量增強圖像效果不明顯，但是從客觀指標上還是可以看出結構張量增強方法對圖像的紋理細節還是有增強效果的.

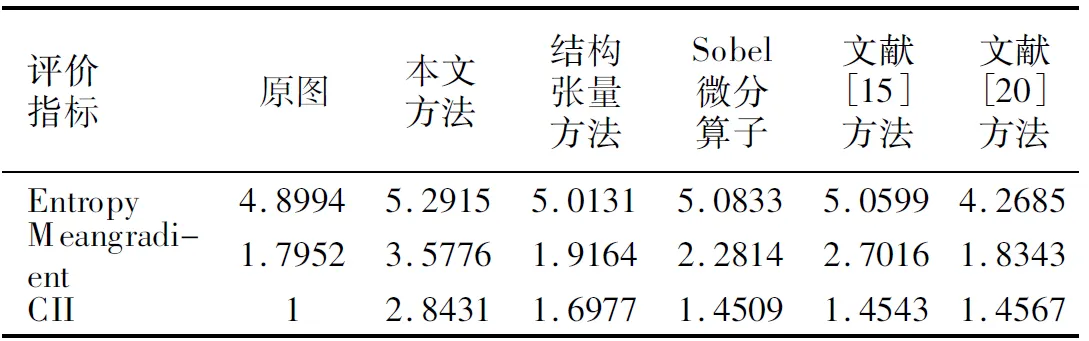
表1 圖4中各圖像評價參數

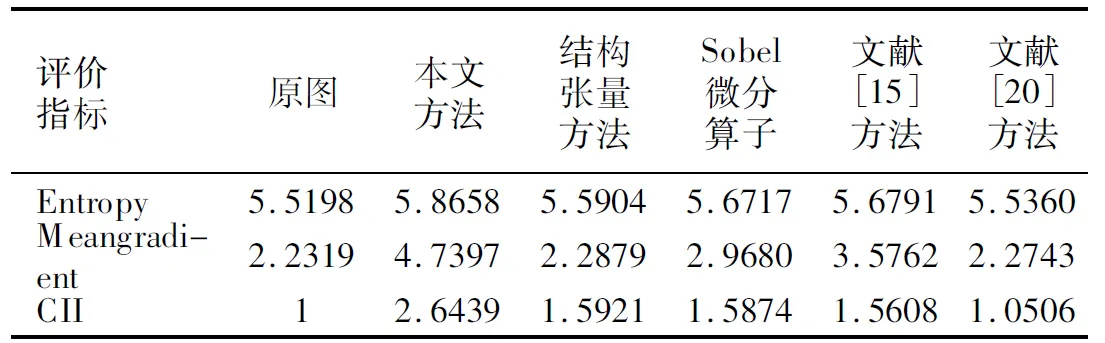
表2 圖5中各圖像評價參數Table 2 Evaluation parameters for each image in fig.5

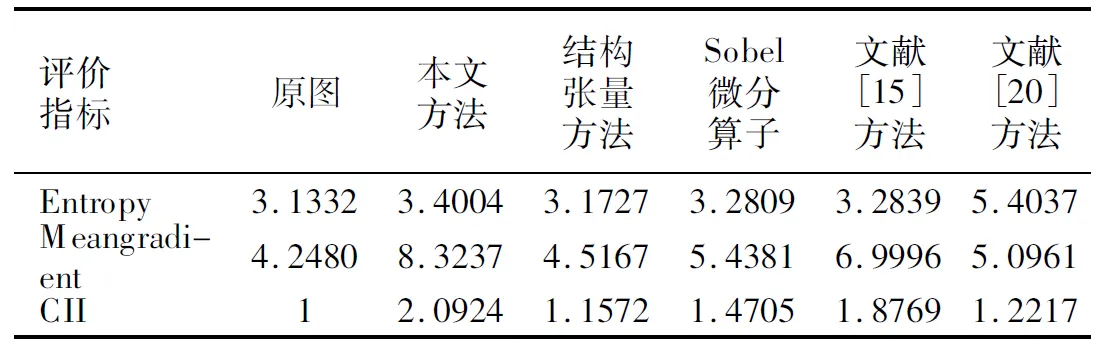
表3 圖6中各圖像評價參數Table 3 Evaluation parameters for each image in fig.6

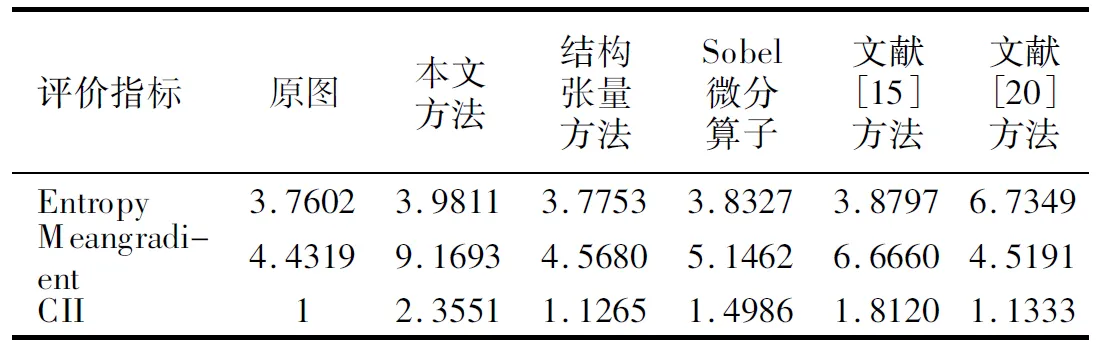
表4 圖7中各圖像評價參數

為了更直觀的表觀各圖像評價參數，做出了各表中評價參數的折線圖，具體如圖8-圖11所示.從折線圖中可以看出，與對比實驗方法以及原圖相比，本文方法具有明顯的高峰走勢.

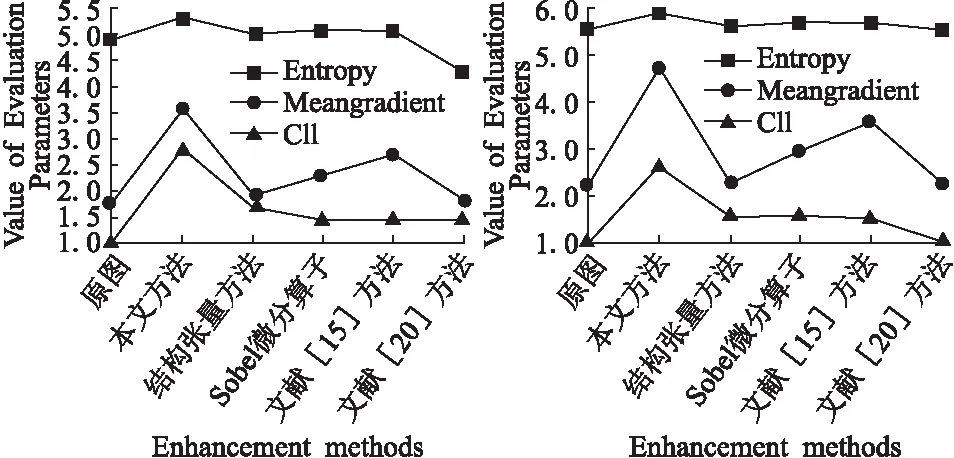
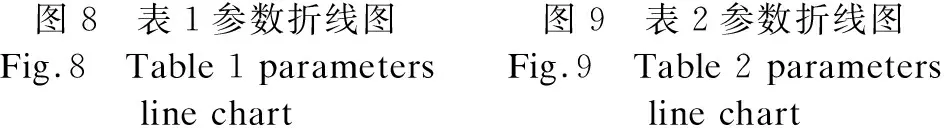
圖8 表1參數折線圖Fig.8 Table 1 parametersline chart圖9 表2參數折線圖Fig.9 Table 2 parameters line chart

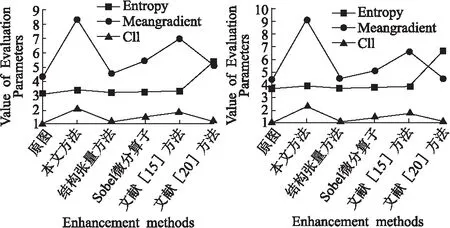
圖10 表3參數折線圖Fig.10 Table 3 parametersline chart圖11 表4參數折線圖Fig.11 Table 4 parametersline chart

4 結束語

本文提出了一種結合分數階微分和結構張量的醫學圖像細微結構增強方法.在基于小波分解的基礎上，低頻信號通過分數階微分算子銳化增強其圖像整體輪廓，高頻信號通過構建的分數階結構張量的特征值之間的相干性度量加權以加強其紋理細節的清晰連續性，最后重構得到增強后的醫學圖像.通過對不同的CT圖像和MR圖像進行實驗，驗證了該方法的有效性.實驗表明本文方法要比分數階微分增強方法得到更豐富的圖像信息，要比結構張量增強方法得到更加清晰連續的紋理細節，且細微結構的增強相對明顯，有著良好的視覺效果，說明此方法具有良好的臨床潛力.但此方法中只用到了結構張量的特征值，對于表示圖像局部灰度變化方向的特征向量還沒有加以應用，在后續的細微結構增強中需要做進一步研究.