GeoGebra軟件在高等數學課程教學上的運用

馬玉青

（唐山學院 河北 唐山 063000）

高等數學作為一門基礎課，是大學課程中的重點、難點學科，該學科知識點多、難度大、理論抽象，讓很多學生感到枯燥、乏味，很難提高學習興趣。將Geo-Geobra運用到高等數學的教學過程中，可以使抽象的數學理論直觀化、形象化，從而幫助學生理解、體會數學知識的形成過程，認識到數學的準確與嚴謹性。

1 GeoGebra軟件簡介

GeoGebra軟件是2002年由美國的Markus Hohenwarter教授研發的一款專用于教學的免費開源的動態數學軟件，它涉及到很多數學的分支，如：幾何、函數、數列、統計、圖表等等。該軟件具有易用易學、操作簡單、功能強大、形象直觀、可動態展示效果等眾多優點。

2 GeoGebra在高等數學教學中的具體運用

2.1 GeoGebra在數列極限概念教學中的運用。數列極限概念的難點就是對于無限增大、無限接近的理解。在傳統教學過程中一般都是老師口頭闡述，學生想象，很難直觀化。這樣學生對概念理解的就不夠透徹，體會不到它的實質，在教學過程中利用GeoGebra，結合課本上的實例，制作相應課件，步驟如下：①創設滑動條n(從1到50增量為1)；②命令區輸入函數③命令區輸入(n，f(n))，右鍵開啟跟蹤；④創設復選框：標題an=，定義為輸入框(f)。

在授課過程中老師拖動滑動條，學生觀察點的變化情況，很容易發現隨著n的增大，點越來越靠近Y軸，這樣學生就很清晰的看到了an的變化趨勢。還可以在輸入框中輸入其他多項式……分別體會觀察當n無限變大時，an的變化趨勢，讓學生充分感受無窮及無限接近的概念，自然而然的形成數列極限的概念。

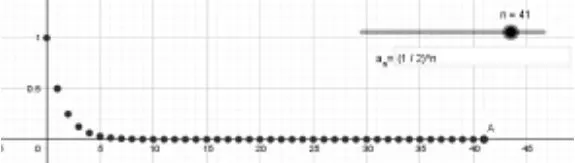
圖1

2.2 GeoGebra在定積分概念教學中的運用。定積分概念是一個典型的過程性概念，對于“分區間—取近似值—求和、取極限”這個過程很多學生理解的不深刻，不透徹，死記硬背，沒能體會真正的數學思想。用GeoGebra輔助該課程教學，學生不但可以直觀地體會“分區間—取近似值—求和、取極限”過程，還可以加深對定積分原型的理解。課件步驟如下：①在命令框中輸入在繪圖區出現該函數對應的圖像；②創設滑動條n(從1到100，增量為1)；③在X軸上設置兩個點A，B；創建曲邊梯形ABCD；④在命令區輸入：上和=上和(f，x(A)，x(B)，n)，下和 = 下和(f，x(A)，x(B)，n)；⑤創設復選框，標題：上和，關聯對象：上和；再把上和函數拖到繪圖區，這樣就設置了上和復選框，同理設置下和復選框；⑥在命令區輸入：曲邊梯形的面積=積分(f，x(A)，x(B))，計算出曲邊梯形的面積。

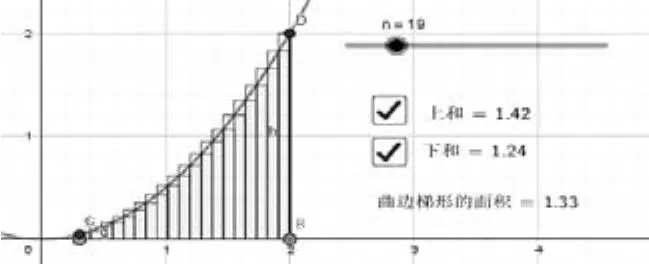
圖2

授課過程中當堂直觀演示：動態移動滑桿n，在n不斷變大的過程中，曲邊梯形被分割的越來越多，對應的上和、下和的值越來越接近曲邊梯形的面積，學生更易理解定積分的實質，提高了教學效率。

2.3 用GeoGebra進行復雜運算。GeoGebra具有大量的運算功能，在高等數學階段我們一般經常運用的計算功能就是求導、定積分。導數、定積分的運算是高等數學學習的一個重要環節，學生一般通過大量的習題體會計算的方法，題目的分類，這時可以借助于GeoGebra來檢驗運算的正確率。

2.4 GeoGebra在空間解析幾何上的運用。GeoGebra具有3D功能，利用它可以很輕松的繪制二元函數的圖像或其他立體圖形，比如橢圓錐面、雙曲拋物面、橢球面等等，我們只需在命令區輸入方程即可，操作起來簡單、方便，產生的圖形逼真、形象，便于問題的學習。