基于對象數量的寬度加權聚類kNN算法

陳 輝，關凱勝，李嘉興 ，2

1.廣東工業大學 計算機學院，廣州 510006

2.廣東省大數據分析與處理重點實驗室，廣州 510006

1.School of Computer Science and Technology,Guangdong University of Technology,Guangzhou 510006,China

2.Guangdong Key Laboratory of Big Data Analysis and Processing,Guangzhou 510006,China

1 引言

k最近鄰算法廣泛用于數據挖掘和數據分析中，這種算法以一個樣本集和一個查詢對象作為輸入，能夠找出距離查詢對象最近（或相似度較高）的k個對象。kNN算法是一種經典的方法，在不同領域有著廣泛的應用[1]，例如數據分類[2-4]、空間數據庫查詢、入侵檢測[5-6]、模式識別[7]、異常值檢測[8-10]、道路網絡查詢[11]、文本分類[12]等。目前很多與kNN算法相關的研究已經提出了許多改進方法用于計算得到精確結果或者近似結果。在損失精度的前提下取得近似結果，這種方式效率較高。與此相反，雖然得到精確結果的算法更為復雜，但是能得到精確的結果。傳統計算精確結果的方法需要遍歷整個數據集，為了解決這個問題，目前很多研究工作都集中在數據的預處理上，其目的是通過計算數據集的一部分來找到查詢對象的k個精確最近鄰（k-NNs）。

一些研究提出基于樹[13-16]的索引結構對數據進行預處理，其索引結構采用二進制分區技術對數據進行預處理，每個樹的葉節點中包含距離相近的對象。kNN算法利用樹的索引結構對數據進行預處理并使用三角不等式修剪不包含結果的節點。高維數據往往具有稀疏而且不相似的特點，使用基于樹的索引結構其內部節點之間將會有較高的重疊度。因此三角不等式將無法修剪大多數的節點。為了解決上述問題，現有工作使用聚類技術將數據集劃分為一些數據集群以得到更好的聚類結果。固定寬度聚類（FWC）[17-18]、k-Means[19]和kNNVWC[20]這三種算法是根據特征空間直接將數據集劃分為若干個子集群，并使用產生的子集群有效地計算k-NNs。FWC算法生成的每個集群都有相同的半徑，這將導致部分集群擁有大量的對象，而部分集群對象數量則很少，這將不利于修剪數據。kNNVWC算法是對FWC算法的一個改進，但是這種方法需要進行復雜的寬度學習，增加聚類的迭代次數，相應的會導致預處理時間的增加。k-Means算法將稀疏分布的對象分給最接近的集群，因此生成的集群可能會有一個很大的半徑。

針對上述方法的局限性，本文提出一種新的基于對象數量的寬度加權聚類算法用于kNN查詢（NOWCkNN）。該算法能產生分布較好的集群，同時建模時間會明顯的減少。本文的貢獻如下：

（1）提出一種新的數據聚類算法，在不同分布的高維數據中生成較好的集群。該算法既有基于tree index聚類算法的優點，也繼承了基于flat index聚類算法的特點。這樣該算法不需要經過大量計算便可得到聚類寬度值，更加有利于劃分數據集，能夠有效地減少迭代次數，降低聚類時間。

（2）基于對象數量的寬度加權聚類算法，提出NOWCkNN算法用于kNN查詢。不同于FWC算法，該算法的寬度值是可調節的，根據其對象數量和調和系數能有效的調節寬度權值，從而減少迭代計算。

2 相關工作

在沒有數據預處理的情況下計算一個給定查詢對象的k個最近鄰需要計算整個數據集，現有的研究工作是為數據建立一個索引結構以避免計算整個數據集。現有的方法大致分為兩類：近似搜索算法和精確搜索算法。

2.1 近似搜索算法

kNN近似搜索算法在處理高維數據時具有很好的性能，但是它的結果精確度較差，得到的k個鄰居中并不都是最近的。局部敏感哈希算法（LSH）[21]包含幾個哈希函數，該方法基于越緊密聯系的對象就越有可能擁有較相近的哈希值這樣一個假設。基于LSH也提出了很多方法，如多探針LSH[22]和LSH森林[23]，前者減少了哈希表的數量但是增加了存儲空間，而后者移除了手動調整參數的必要性。最近以空間分區結構為基礎的算法被用于kNN的近似搜索，例如隨機kd樹[24]和k-Means優先搜索樹[25]，這些算法比LSH算法在近似查詢方面有更好的表現。

2.2 精確搜索算法

2.2.1 Tree-Based Index

目前有很多研究使用二叉樹[14，26-27]（例如KDTree[26]）來構建數據集的索引結構，每個樹的葉節點都包含彼此相近的對象。這些葉節點的集合組成父節點，其父節點都包含彼此相近的子節點，這個過程被遞歸的調用，直到根節點包含所有節點。kNN算法利用基于樹的索引方法，使用三角不等式來修剪不包含結果的節點。每個基于樹的索引以不同的遞歸調用方式構建索引結構，樹型索引的主要不足在于采用二進制分割技術構建索引結構。該方式對于對象分布未知且維度較高的數據集并不是一個很好的解決方法。高維數據往往是比較少而且也不相似的，基于樹的索引結構其內部節點之間將會有很高的重疊度，因此使用三角不等式將無法修剪掉大多數的節點，kNN算法通常還是需要遍歷整個數據集（或數據集的大部分）。

2.2.2 Flat-Based Index

當樹節點之間的重疊度較高時，樹結構就失去了作用。受此啟發，一些研究提出Flat-Based Index，例如FWC[17-18]、k-Means[19]和 kNNVWC[20]算法，這些方法使用聚類算法直接將數據集分成集群來獲取更好的分區效果，并使用這些集群來有效地計算k-NNs。

現有的Flat Index聚類方法可能會產生分布不均的集群，其生成的集群大小差別很大，這會降低三角不等式的修剪效率。例如，k-Means將稀疏的對象分配給其最近的集群，因此這些集群的半徑會很大，與其他集群重疊度就會很高，這也就增加了kNN算法的查詢時間。同樣地，FWC算法生成集群中的對象數量并不均勻，該算法的時間復雜度為O(cs)，其中s為對象的數量，c為產生集群的數量。設置一個較小的固定寬度值可以防止較大集群的產生，但是這將會導致產生大量的集群，無疑會增加預處理時間。針對FWC算法的不足，Almalawi等人[20]提出一種寬度自學習聚類算法，該算法把數據集分割成多個不同寬度大小的集群。但是這種方法在集群再次劃分時需要進行集群寬度計算，對于生成有較多對象的集群，需要經過多次迭代才能很好的分割數據，這會導致聚類過程需要不斷的迭代進行。基于此種情況，本文提出一種基于對象數量的寬度加權聚類算法用于kNN查詢，每個集群的寬度在聚類時根據對象數量進行寬度自學習。

3 提出的寬度加權聚類算法

針對上述方法的不足，本文提出一種基于對象數量的寬度加權聚類算法，該算法是在FWC算法的基礎上進一步聚類劃分。本章首先介紹FWC的聚類步驟，然后介紹NOWCkNN算法的兩部分：聚類和查詢。

3.1 FWC算法

定義1待聚類數據集DS：DS={O1,O2,…,On}，其中Oi為數據集DS的第i個對象，n為對象的個數。

定義2對象O={a1,a2,…,aj,…,am}，其中aj為對象Oi的第 j個屬性，m為每個對象屬性的個數。

定義3聚類輸出集群集合C={C1,C2,…,Ct,…,Cn}，其中n為聚類生成的集群數，Ct表示第t個集群。

定義4集群C={Cd,Cc,Cw}，其中Cd用來存儲生成集群的數據，Cc存儲集群的中心，Cw存儲集群的半徑寬度。

固定寬度聚類（FWC）算法[17-18]是將數據集分成多個具有相同半徑的集群。算法1描述了FWC的算法步驟，表1是對算法1中一些符號和函數的定義。FWC算法每次分割一個數據集。首先把數據集中第一個對象設為第一個集群的中心（5～8行），對于下一個對象需要先計算距離其最近的一個集群did，并與固定寬度值W比較（第6行）。如果計算距離值did大于W，則需要重新創建一個集群并把此對象插入該集群（第8行）；若距離did不大于W ，則把此對象插入到該集群中（9～10行）。比較距離did與該集群的半徑wid，若小于半徑wid，則需要重新更新其半徑值（11～12行）。算法依次循環執行，直到數據集中的對象都被分到不同的集群中。

表1 算法1的符號和函數定義

算法1 FWC算法

1.InputDS

2.OutputC

4.n=0

5.forOiinDS.objects

7.n=n+1

8.addOitoCnew

9.else ifdid≤W

10.addOitoCid

11.ifdid＜wid

12.setwid=did

13.returnC

FWC算法的性質限制了它在異常檢測中的應用，創建具有固定寬度的集群集合可能無法修剪大多數的數據對象。Eskin等人[17]提出的FWC算法雖然可以將數據集分解成較小的集群，并用這種方法找到查詢對象的k-NNs。然而當數據分布不均時，這種分解效果并不是很好，雖然kNNVWC算法[20]對此進行了改進，但是其寬度計算量偏大，算法迭代次數較多，不能很好地控制生成集群的大小，同時該算法寬度的計算會隨著維度的升高而增加。

聚類產生較好的集群能夠有效的提高kNN算法的修剪率。基于此理論，需要盡可能的生成效果較好的集群。數據的聚類需要經過大量的計算，要產生效果較好的集群還需要避免計算量過大。集群的大小或者集群數量都能影響聚類的效果，集群的寬度決定集群的大小和產生集群的數量。因此需要調整集群寬度的大小，使其能夠產生質量較好的集群。每個集群的寬度與集群中的對象數量正相關，根據對象數量調整寬度再設置一個系數調節大小，可以有效地控制不同集群寬度的產生。例如，超過閾值具有相同對象數量的集群，其集群寬度可能會不相同。對于寬度較大的集群，其數據相對稀疏，設置較小的系數，使寬度權值相對較大，這樣可以減少集群的數量，避免產生具有極少對象的集群；對于寬度較小的集群，其數據相對稠密，設置較大的系數，使寬度值相對較小，這樣可以減少迭代。

3.2 基于對象數量的寬度加權聚類算法

3.2.1 集群寬度加權計算

令D為要進行聚類的數據集，s為數據集中的對象數量，函數Quotien(a,b)返回a/b的整數部分，用ωCn表示第n個集群的半徑寬度，p為調和系數。此過程中有一個變量：閾值β，這是用來限定集群大小的閾值，集群中的對象數量不能超過閾值β，其寬度表達式如下：

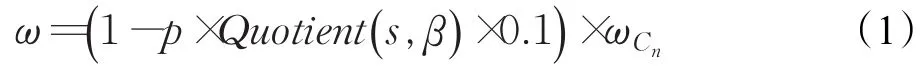
這里調和系數 p的大小和函數Quotien的范圍將會影響到聚類的效果，在4.2節中會分析 p的大小和函數Quotien的范圍。

3.2.2 聚類過程

該過程將數據集劃分成多個集群，以解決在高維空間中數據對象的聚類問題。但是，數據集中在數據比較集中的區域可能會有大的集群產生，因此需要將產生具有較多對象的集群再次進行劃分，直到每個集群的大小都不超過所規定的閾值（最大值）。本文在算法2中總結了聚類過程，表2是算法2的一些符號和函數定義。

算法首先把數據集劃分為具有固定寬度的集群（第3行），初始化迭代次數為1。然后循環找出對象數量大于β的集群，把這些對象數量大于β的集群添加到MultiClusters中（5～7行），把對象數量小于 β的集群添加到LessClusters（第9行），同時標記對象數量小于β的集群為不可再分（第10行）。對于對象數量大于β的集群需要重新計算其寬度值，用公式（1）的方法計算集群下一次聚類時的寬度值（第13行），然后繼續對該集群進行劃分，迭代的劃分集群直到所有集群中的對象數量都不大于β（第16～17行）。每次迭代后，迭代次數都要加1（第18行）。

表2 算法2的符號和函數定義

算法2 NOWC算法

1.Input：data

2.Input：β

3.Clusters=Algorithm1（data，W）

4.t=1

5.foreach cluster in Clusters

6.ifcluster.objects＞β

7.put cluster in Multi Cluster

8.else

9.put cluster in Less Clusters

10.LessClusters←NonCluster

11.for each cluster in Multib Clusters

12.D←cluster.data

13.w ← equation（1）

14.tmp Clusters← Algorithm1（D，w）

15.put tmp Clusters into new CLusters

16.for new Clusters

17.go to line 4

18.t+=1

19.return

同時設定其迭代上限為t（t通常小于等于3），由于迭代次數越多生成集群的數量就會相應的增加，集群中對象的數量就會越來越少。此時進行kNN查詢時，這會增加計算消耗。在每次迭代時，設定迭代聚類產生的集群數量都不大于前一個迭代聚類產生的集群數量，這樣可以防止較小集群的產生，提高聚類質量，提升kNN查詢時的修剪率。

3.3 kNN查詢過程

定義5（k-最近鄰（kNN））一個查詢對象q的k個最近鄰居到q的距離小于數據集中剩余對象到q的距離。設Uqk={X1,X2,…,Xk}是查詢對象q的k個最近鄰對象，MAXk表示查詢對象q與數據中所有對象的距離按從小到大排序的第k個距離值，則其k個最近鄰表示為：

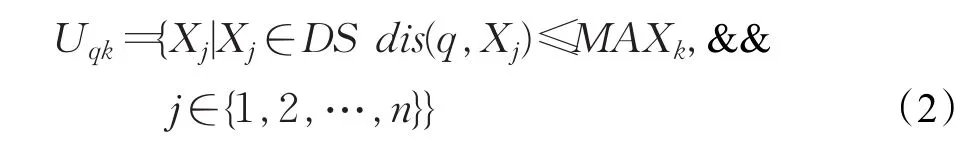
定義6（候選集群）對于給定的查詢對象q，其中Li={O1,O2,…,Ok}是q在集群Ci的最近鄰對象，wk表示q到其k個最近鄰中最遠對象的距離，wi是集群Ci的半徑寬度，C={C1,C2,…,Cn}是集群的集合，其中，如果，則集群Cm是 q的一個候選集群。

表3 算法3的符號和函數定義

算法3 NOWCkNN算法

1.Input：Clusters

2.Input：k

3.Input：q

4.Output：kNNObjects

6.CluDisID ← SortClustersByq（Clusters，q）

7.foreach{ID，Distance}in CluDisID

8.tmpCluster=getCluster（ID）

9.kNNObjects=kNNObjects∪tmpCluster.Objects

10.If|kNNObjects|＞k

11.break

12.{wk，kNNObjects}=kNNDistance（kNNObjects，q，k）

13.foreach CluDisID

14.tmpCluster← getCluster（ID）

15.if（tmpCluster.radius+wk）＞CluDisID.Distance

16.put tmpCluster.Objects in kNNObjects

17.go to line 12

18.else（tmpCluster.radius+wk）＜=CluDisID.Distance

19.continue

20.return kNNObjects

如圖1的B所示，Ci是要進行計算的下一個集群，{O1,O2,O3,O4,O5}是集群Ci的對象，其中O1是集群Ci的中心，集群半徑radius為23.5。查詢對象q到集群中心的距離為w=32.4，以q為圓心，wk為半徑畫圓，該圓到集群中心O1的距離小于兩個圓半徑的距離之和（第15～16行），即32.4＜23.5+14.7，則此聚類中可能存在比wk更近的對象，然后把此集群添加到候選集群表中，并把候選集群中的對象添加到候選對象表中，重新計算其k個最近鄰和到第k個鄰居的距離wk（第17行）。如圖1的A所示若兩個圓沒有相交，則說明此集群中不存在比wk更近的對象了，此集群被修剪。算法循環遍歷每個集群，直到所有集群到查詢對象q的距離都大于其集群半徑和wk之和（如圖1的A所示），則算法停止，返回這k個最近鄰對象（第20行）。

時間復雜度分析：

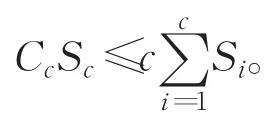
4 實驗結果與分析

本章中，在各種數據集中驗證NOWCkNN算法的性能，實驗從三方面分析算法的性能：（1）建模過程消耗的時間；（2）進行距離計算的對象數量；（3）kNN查詢所用時間。將四個算法KDTree、kNNVWC、FWC、k-Means與NOWCkNN算法進行比較，每次實驗時將整個數據集作為訓練集，隨機從訓練集中選取一些對象作為測試集，所有測試對象的平均值作為總體結果。所有算法都是用Java實現，實驗操作系統為macOS，CPU頻率為2.9 GHz，內存為8 GB。

4.1 數據集

選用不同維度特征空間的數據集用于測試所提出算法的性能，這些被選擇的UCI公開數據集來自各個領域，被廣泛地應用于數據挖掘，只是使用它們來驗證NOWCkNN算法在k最近鄰搜索中的性能。這些數據集的簡要描述如下：

shuttle數據集有43 500個對象組成，每個對象有9個數字特征表示，它用于歐洲StatLog項目測試機器學習的性能；

arcene數據集通過SELDI獲得的觀測數據，用于從正常模式中辨別出癌癥，該數據集有900個對象，每個對象有1 000個特征屬性；

waveform數據集由5 000個對象組成，每個對象有40個特征，其中有一些噪音數據；

圖1 基于三角不等式的NOWCkNN查詢實例

spambase數據集有4 601個（電子郵件）對象，其中包含1 443條垃圾郵件，每個對象有57個屬性；

optdigits數據集是識別0～9的數字，optdigits數據集訓練集有3 823個對象，測試集有1 797個對象，每個對象有65個屬性；

madelon是NIPS 2003比賽中5組數據集中的其中一組，共有數據對象4 400個，每個數據有500個屬性；

gasSensors是來自16個傳感器的13 910個對象，每個傳感器提取8個特征，這使每個對象有128個特征屬性；

DUWWTP數據集來自城市廢水處理廠的傳感器的日常測量值，由527個對象組成，每個對象有38個特征。

4.2 參數的設置

不同的算法需要不同的參數設置，對于FWC算法最重要參數的就是集群寬度，而k-Means方法最重要的參數就是k值的選擇。文獻[19]提出的k-Means方法證明了k值為2時效果最佳，其中s為數據集的大小。對于FWC算法，找到合適的寬度值是非常困難的，因此本文選擇產生集群數量盡可能接近2。本次實驗中KDTree方法的葉子大小設置為40，該數值對于大多數的數據集能取得最佳效果。由于本文所提方法不確定所產生的集群數，因此測試了β的各種取值，選擇在不同維度、不同大小以及不同領域的數據集進行測試。如圖2所示，橫坐標表示生成的集群數量，調整β值改變生成的集群數量。如圖2所示，各個數據集聚類產生集群數大約在到3之間時算法的性能較好，因此把生成此范圍集群數量的β值作為最優β值。

式（1）中調和系數 p的大小將會直接影響到生成集群的數量，而函數Quotient的取值范圍也會影響到算法的性能。一個較大的 p值會使每次迭代計算得到的寬度值都接近于最小寬度值，這會導致有大量的集群產生。函數Quotient的取值范圍越大則迭代的寬度值越小，其取值越小的情況下其迭代得到的寬度值越大，寬度值較小則會產生大量的聚類，較大則會增加迭代次數，影響算法性能，因此產生較好的聚類效果依賴于調和系數p的大小和函數Quotient取值范圍。在這次測試中選擇的數據集在維度、數據集大小和疏密度方面都有差異。用對象距離修剪率ord表示數據集的修剪效率，其計算表達式為：

其中，s為數據集的大小，Cm為在數據集中找到k個最近鄰參與計算的集群數量。

如圖3所示，較高維度的數據集arcene中寬度值較大，數據較為分散，p值越大其聚類寬度值在迭代時減小的越快，而產生聚類的對象數量很難影響函數Quotient的取值。從圖3（a）中可以看出，提出算法在p=2時各個數據集都具有較高的數據修剪率，而函數Quotient范圍在QMAX=6時（即取值范圍2至6之間）效果較好。而在數據集shuttle、pendigits和spambase中，p的值為2或3時較好，函數Quotient范圍在2與6之間時其數據修剪率較高，效果最優。因此，在聚類時參數 p的值一般設為2或3，其函數Quotient范圍為2至6。對于 p值較大時，可能也會取得較好的結果，但是這樣會導致一些數據集有大量的集群產生，這樣不利于基于三角不等式的kNN查詢。同時Quotient函數范圍小于2或者大于7時，如圖3所示算法的性能明顯下降，根據算法的時間復雜度降低迭代次數能夠有效地降低計算量。因此，當Quotient函數范圍小于2時，寬度值減少的速率較慢，這無疑會增加迭代次數，當范圍大于7時寬度值較小，則會產生大量的集群。

從圖3中可以設定Quotient(s,β)函數的范圍為2≤Quotient(s,β)≤6（即QMAX=6），Quotient函數值大于6的時候，設其值為6，特別地，Quotient函數值為0或1的時候，設其值為2。使用式（1）中寬度計算公式，設定其迭代的子集群寬度權值最小為父類寬度值的0.4倍，最大為父類寬度值的0.8倍。聚類中對象數量越多其寬度值權值則越小，這樣可以減少算法迭代的次數，同時能夠減少聚類時間。其函數范圍表示如下：

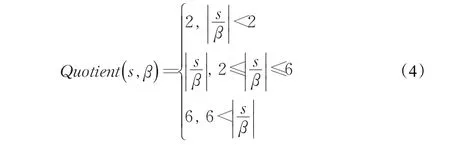
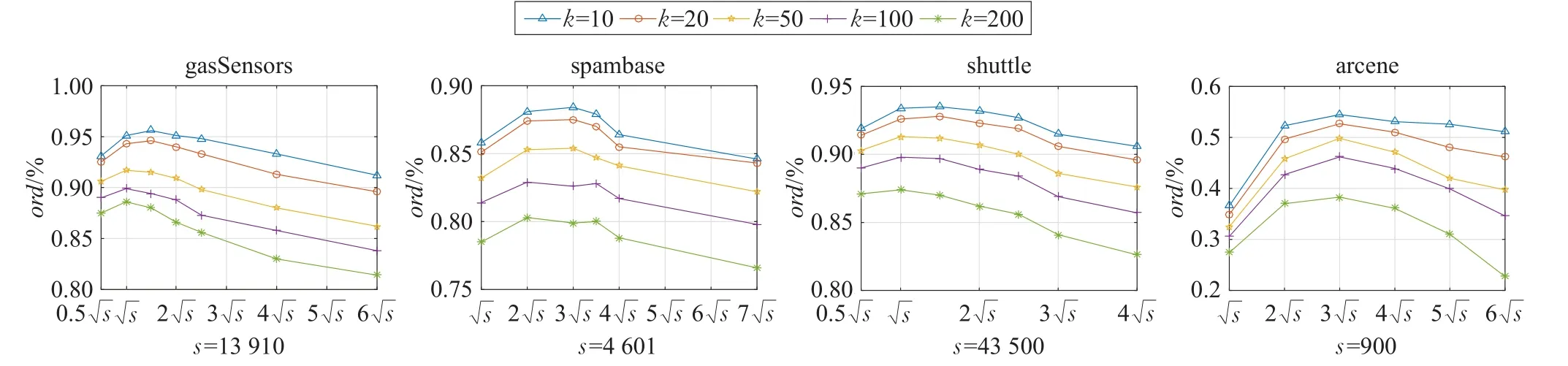
圖2 不同β值對應生成的集群數量對算法性能的影響

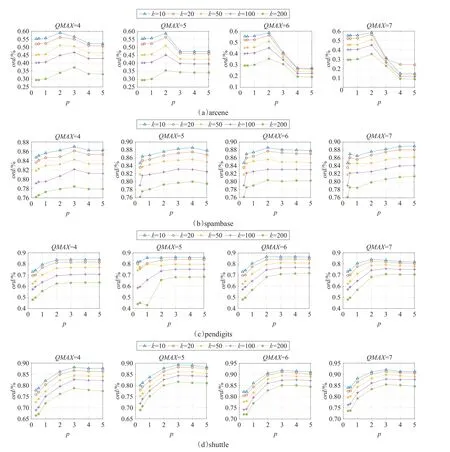
圖3 不同p值和不同函數Quotient的范圍對本文算法性能的影響

4.3 性能指標

原始kNN查詢方法的不足在于它需要一個冗長的計算時間，這是由于對數據集中的每個對象都要進行距離計算。因此現有的改進kNN搜索方法的主要目標就是減少數據集中對象的距離計算，為了衡量這種方法的效率，采用建模時間、kNN查詢時間和數據集中參與距離計算對象的數量作為評價標準。

4.3.1建模時間

這些方法都是kNN搜索之前的預處理步驟，每個方法都以自己的分解技術來構建索引結構。圖4顯示了這幾種方法在每個數據集上的建模時間，從圖中可以看出k-Means方法是最差的，而且會受到數據大小的影響，固定寬度算法（FWC）則是第二差的方法，相較于kNNVWC與NOWCkNN方法，FWC算法的建模時間通常是比較長的。而KDTree方法在低維度數據集中效果較好，在高維度數據集中建模時間較長。kNNVWC由于每次進行聚類迭代時，寬度計算都會消耗大量的時間。本文所提方法NOWCkNN建模時間相對較短，對比kNNVWC算法，NOWCkNN能減少寬度學習時的對象計算消耗，對于不同數據集都能得到較好的聚類集群。對于高維數據，本文所提方法的建模時間相較于其他方法有明顯優勢，建模時間低于其他方法，對于其他維度的數據也有很好的效果。

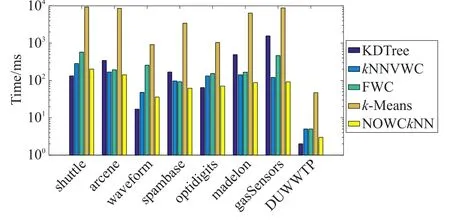
圖4 本文方法和其他方法在每個數據集上的建模時間

4.3.2查詢時間加速率

對比原始kNN算法評估所提出算法的性能，令ty表示原始kNN算法的查詢時間，tn表示運行一個算法的kNN查詢時間，算法的查詢時間加速率sr表示為：

查詢時間加速率反應了改進算法對于原始kNN算法的影響程度，即查詢時間加速率為2說明該算法相較于原始kNN算法提高了1倍，加速率為0.5說明算法比原始kNN慢了1倍。同時，當加速率為1時說明，該算法和原始kNN查詢時間相同，也就是說對數據進行預處理后并沒有減少查詢時間，反而有可能增加查詢時間。因此把sr=1作為一個分界點，大于1說明該方法效果較好，能夠減少kNN查詢的時間；不大于1時表示數據的建模沒有減少查詢時間，說明該數據集不用預處理即可實現查詢。

在kNN查詢時，把k值設為5種不同的取值，分別為10、20、50、100、200，圖5顯示了不同方法在不同數據集以及不同k值的查詢時間加速率。從圖中可以看出KDTree方法在高維數據中效果不佳，但是在維度較低時能夠得到較好的結果。在一些大的數據集中（如shuttle、gasSensors），雖然FWC、kNNVWC、NOWCkNN、k-Means方法得到了很好的結果，但是綜合來說NOWCkNN是最有效的方法。對于一些中等數據集KDTree方法效果較差，k-Means方法受到數據集分布的影響表現出稍差的結果。在高維數據集（如arcene、madelon）中，數據量較小時，NOWCkNN與kNNVWC其查詢時間加速率都能大于1，本文方法相比kNNVWC能夠提高10%，而且NOWCkNN在建模時間上明顯小于kNNVWC。在中等維度的數據集中，數據量較大時（gasSensors），KDTree查詢效率較低，而k-Means受到數據分布的影響每次查詢時間并不固定，并且大部分的查詢時間加速率都低于FWC，kNNVWC能把數據集分成更小的聚類，其查詢時間加速率優于FWC算法。但是NOWCkNN能根據聚類數量的大小設定寬度值的范圍，這能得到效果更好的集群，因此其查詢時間加速率要略優于其他幾種方法。因此在高緯度數據集中，本文方法的查詢時間加速率要明顯優于其他方法。

5 結束語

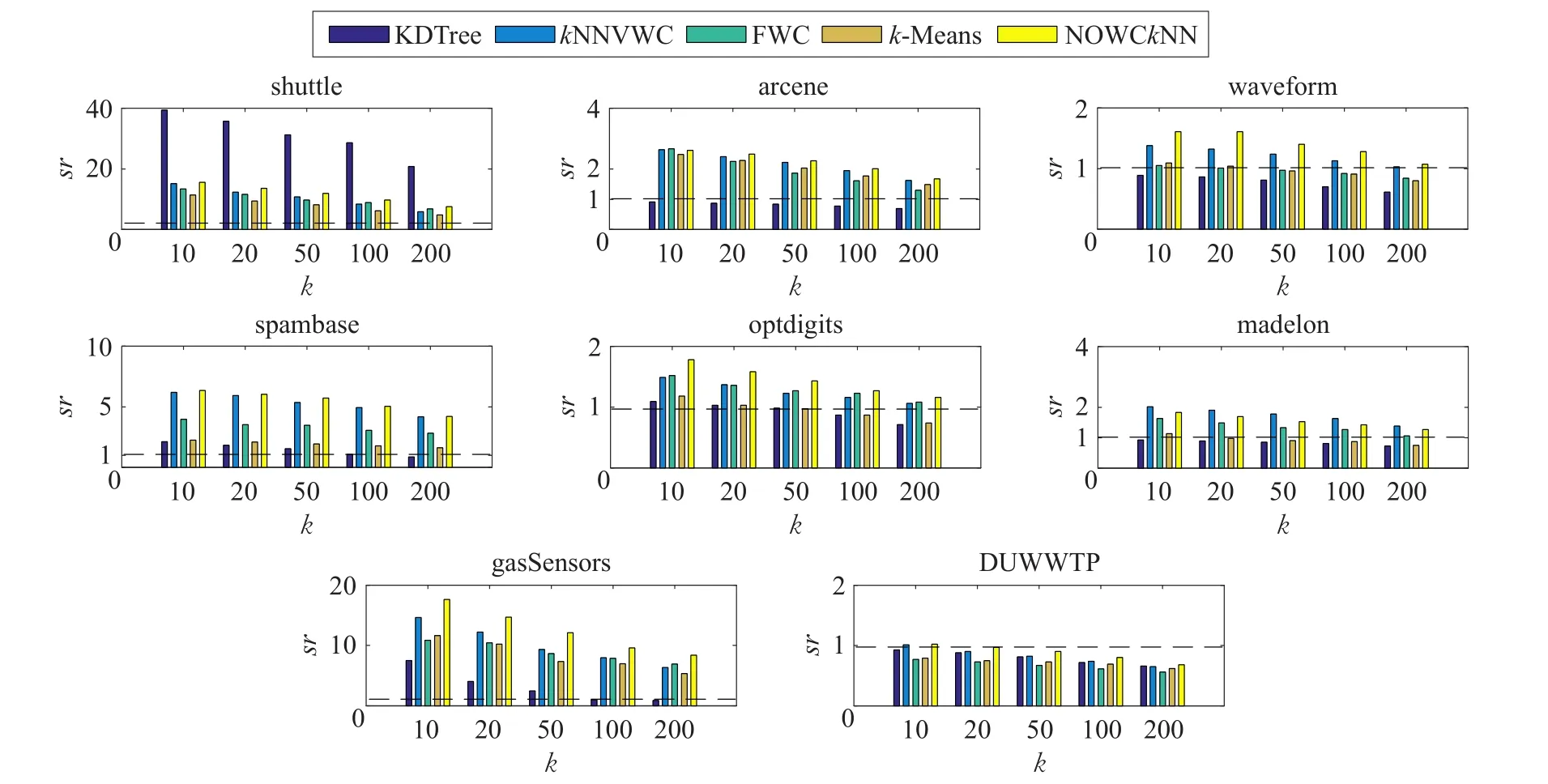
圖5 本文方法與其他方法在不同k值上的查詢時間加速率

本文針對kNN算法計算量大的問題，提出一種基于基于對象數量的寬度加權聚類算法用于kNN的查詢（NOWCkNN）。該算法基于集群內的對象數量和調和系數計算寬度權值，然后迭代的將集群再次劃分，這種方法能使集群的分離效果更加優化，在不同維度的數據集中分離出效果較好的集群，分類的結果能夠在kNN查詢時，使用三角不等式最大化地修剪不太可能的對象。在實驗中，使用8個UCI公開數據集驗證所提出方法，實驗結果顯示，與現有方法相比所提出的算法能夠減少聚類迭代的次數，減少建模時間，增加kNN查詢的修剪率，特別是在高維度、數據量較大的數據集中效果更好。同時本文所提方法具有通用性，在不同維度、不同分布的數據集中都有較好的實驗結果。在今后的工作中，將重點關注聚類的改進，進一步減少預處理的成本和查詢時間，會使用并行計算以降低預處理時間，同時還會選取新穎的距離（相似度）計算公式；同時將會分級控制產生的集群，以便獲取更好聚類結果用于kNN查詢。