組合型冪指函數三穩態隨機共振微弱信號檢測

張 剛，高俊鵬

(信號與信息處理重慶市重點實驗室(重慶郵電大學)，重慶 400065)

0 引言

微弱信號檢測應用范圍廣泛涉及到光學、電磁學、數理學、物理力學、地質學、材料學等學科，因此微弱信號檢測成為當前研究的熱點[1]。微弱信號檢測技術是用來檢測噪聲淹沒下的有用信號，一般采用抑制噪聲技術來提高信噪比(Signal-to-Noise Ratio, SNR)，常規方法有時頻分析[2]、經驗模態分解法[3]、小波變換[4]等，這些方法在降噪的同時會使得有用信號受損。針對這個問題，本文采用隨機共振方法，使噪聲的能量向檢測頻率附近處發生轉移，這種能量轉移現象屬于非線性系統中的一種動力學現象，因此構造不同的非線性系統模型，使得微弱信號的檢測性能也不同。1981年Benzi等[5]首次提出“隨機共振”(Stochastic Resonance, SR)的概念。目前隨機共振理論已成為非線性科學領域的一個熱點課題。隨機共振現象是一種力學現象，它表征著驅動周期、噪聲、系統參數三者能夠達到協同效應[6]，使得噪聲的能量根據洛倫茨分布逐步向低頻有用信號轉移，從而提高系統輸出信噪比，有效提高微弱信號檢測性能。隨機共振是根據線性響應理論和絕熱近似理論[7],適用于低頻(f≤1 Hz)的有用信號，但實際應用中，檢測有用信號往往是大頻率的，于是近幾年學者提出了許多技術解決大頻率這個問題，比如二次采樣[8]、移頻變尺度[9]、歸一化尺度變換[10]等。以上方法都是從有用信號頻率角度出發，然而在隨機共振系統中，也可以從構造勢函數的角度出發，不斷提出一些新的勢函數模型，如文獻[11]提出了冪函數型單勢阱隨機共振的廣義隨機共振；文獻[12]研究了Levy噪聲下一階線性系統的弱信號復原分析；同時文獻[13]也提出Levy噪聲激勵下的冪函數型單穩態隨機共振特性分析；文獻[14]研究了基于冪函數型雙穩態隨機共振的故障信號檢測方法。這些函數模型構造使得隨機共振系統更加多樣化，大大提高了隨機共振檢測能力，應用范圍也比較廣泛。

由于勢函數模型多樣化出現，隨機共振效應僅驅動信號、噪聲、系統參數三者達到協同作用從而實現更好的隨機共振現象對應的輸出信噪比，對參數優化有了一定要求，而不同勢函數模型存在系統一個參數或多個參數，經過多年研究，有一些自適應參數尋優方法，比如果蠅算法[15]、人工魚群算法[16]、遺傳算法[17]、粒子群算法[18]等。在實際工業應用實踐中，大型機械的軸承是工業生產中不可或缺的設備，通過隨機共振微弱信號檢測到軸承滾動的故障頻率，能夠減少工業生產中不必要的經濟損失。為提高生產效率，學者們也做了大量研究工作，如文獻[19]提出了級聯雙穩隨機共振降噪下的經驗模態分解，文獻[20]基于多穩態隨機共振系統提高輸出信噪比實現軋機齒輪故障的診斷。

本文結合經典雙穩態系統模型和高斯勢阱(Gaussian Potential, GP)提出了一種新的組合型冪指函數三穩態隨機共振模型。首先，通過對系統4個參數分析驗證能夠產生隨機共振現象；其次，運用人工魚群算法進行相應的參數尋優，檢測多頻信號；最后，通過工程實踐，結合希爾伯特變換技術，驗證了此方法具有更好的應用前景和實用價值。。

1 相關理論

1.1 雙穩態系統下雙勢阱模型

雙穩態系統中雙勢阱模型中，勢函數Um(x)有一對對稱的勢阱，雙穩態系統勢函數表達式[14]如下:

(1)

其中：a、b都是大于零的數，圖1表示系統參數對于雙勢阱的影響。

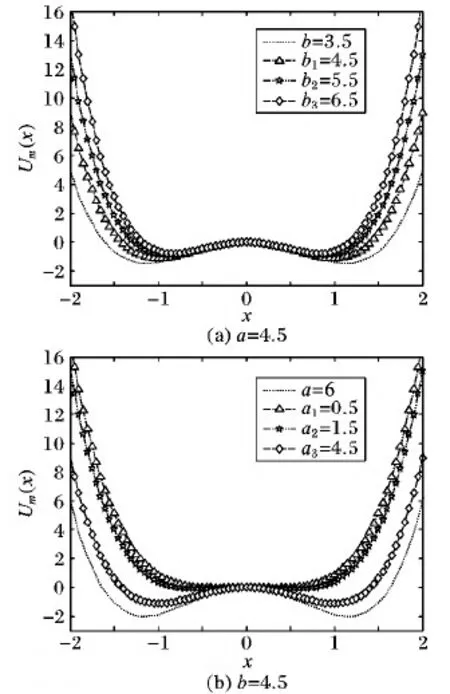
圖1 雙勢阱勢函數

圖1(a)中固定數值a=4.5，當a值不變時，通過調節b的變化，可以得出一個結論：隨b的數值增加勢壘高度越來越小。圖1(b)中固定數值b=4.5，當b值不變時，通過調節a的變化，可以看出：勢阱高度變化隨a值增加勢壘高度越來越大，與圖1(a)正好反相關。

1.2 GP勢函數模型

被廣泛應用于核物理學的GP勢阱模型表達式[21]如下:

Ug(x)=-Vexp(-x2/R2)

(2)

其中：V表征勢阱深度，R表征為勢阱寬度。圖2是GP單勢阱圖形，GP勢函數的特別之處在于在單勢阱兩端都是收斂于零的勢函數。圖2(a)中固定V=3，可以看出隨著R的增加，GP勢阱壁逐步變得平緩；圖2(b)中固定R=0.5，V從大到小變化時，GP勢函數的勢阱高度逐步變小。所以可以通過分別調節GP單勢阱的系統參數V、R來改變勢阱的高度和勢阱壁的陡峭度的大小。

圖2 GP單勢阱勢函數

1.3 冪指函數的組合模型

基于上述兩種模型的一些特性，將雙穩態勢函數與Gaussian Potential單勢阱勢函數相結合，提出一種新型的冪指型三穩態勢函數模型，勢函數如下：

U(x)=Um(x)+Ug(x)=

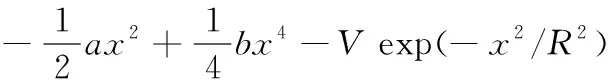
(3)

當系統參數a=6、b=4.5、V=2、R=0.3時構造出如圖3所示的冪指型三穩態勢函數。由圖3可知，該函數有一對對稱的勢壘，可通過調節a、b、V、R使冪指型三穩態勢函數的結構發生變化。由于加入GP勢函數后，把原有的雙穩態改變成了三穩態，使震蕩粒子在雙勢阱變成三勢阱躍遷，提高了噪聲的利用率進而提高輸出信噪比，從而達到更佳的隨機共振現象。通過改變系統參數，可以在雙勢阱和三勢阱之間進行轉換，因此這個新型模型具備了雙穩和三穩的一些特性。

圖3 組合型冪指函數三穩勢函數

2 組合型隨機共振系統

2.1 共振系統方程

用朗之萬方程來描述粒子運動的數學模型，方程如下:

(4)

其中：s(t)是驅動周期；n(t)是期望為零、方差為2Dδ(π)高斯白噪聲，其中δ(π)期望為0、方差為1，D是噪聲強度。通過把式(3)代入式(4)中得到式(5)：

(5)

(6)

(7)

勢函數的解的個數符合一般三穩態的勢函數，需要數值仿真來驗證式(4)、(5)能出現隨機共振現象。

圖4 方程組解的個數

2.2 參數優化對系統影響

目前隨機共振的測量指標有許多種，例如相關系數、特征頻率峰值、功率譜放大系數、信噪比增益、平均輸出信噪比等，本文主要采用的是平均輸出信噪比。信噪比定義如下:

SNR=10 lg(S/N)

(8)

其中：S是原始驅動周期信號，N是噪聲信號 。平均輸出信噪比定義為:

(9)

其中n表示仿真系數。

首先考慮噪聲強度D對平均輸出信噪比的影響。通過調節其他參數取a=1.5，b=3.5，V=3.7，R=2.5，D以在0.01～5以0.05為步長取值。經過100次實驗取平均，可得到圖5。可以看出，隨著噪聲強度增加導致平均輸出信噪比先增加后減少，在某一個噪聲強度時達到最大輸出信噪比。因此，組合型冪指三穩隨機共振具有隨機共振的現象。

圖5 組合型冪指函數三穩態隨機共振系統的平均輸出信噪比隨著參數D的變化

圖6為四個系統參數和系統輸出的平均輸出信噪比之間的函數關系，它們共同的現象是存在一個單峰值曲線，規律都是先增加后減少的趨勢，可以看出構造組合方程與系統參數具有非線性關系。圖6表明系統參數對系統輸出的能量分布起著十分重要的作用，因此調節系統參數能使組合系統產生隨機共振現象。上述分析表明，在組合型共振系統模型中，通過調節四個系統參數使得SR系統中信號和噪聲的能量分布發生變化，可以實現噪聲能量向信號能量轉移，從而達到用噪聲增強有用信號的效果。

圖6 系統參數與系統輸出SNR的關系

如圖6所示，調節系統參數，能夠使得系統達到隨機共振現象，而單獨對每個參數分別優化，使系統達到隨機共振現象，會忽略參數之間相互作用，人工魚群算法可以對所有系統參數進行并行優化，克服參數相互作用的缺點，該算法魯棒性強，對初始值不明感，易于設置初始值的范圍。該算法的主要行為有：覓食行為、聚群行為、追尾行為和隨機行為。設置人工魚群算法的參數，包括魚群個體的數量N，魚群的活動范圍LBUB(Low Bound Up Bond)，魚的感知范圍Visual。魚的最大移動步長step，嘗試次數try_number， 最大迭代Maxgen，擁堵因子δ，di, j表征人工魚個體之間的距離。將目標函數定義為Y=f(x)=SNR。算法實現步驟如下：

步驟1 初始化N=20條人工魚，感知范圍Visual為[0，20],移動步長step=0.1,擁擠因子δ=0.618，嘗試次數try_number=50,當前迭代次數gen=0,最大迭代次數Maxgen=100,當前覓食行為次數n。

步驟2 計算并篩選魚群所有個體當前狀態最優的目標函數作為當前公告板上的初始化值。

步驟3 執行聚群行為。設人工魚群當前狀態為Xi，在當前鄰域內(di,jδYi，表明周圍不太擁擠，則朝伙伴的中心位置前進一步，否則執行覓食行為(步驟5)。

步驟4 執行追尾行為。設人工魚群當前狀態為Xi，在當前鄰域內(di,jδYi，表明伙伴Xj的狀態具有較高食物濃度，不存在魚群個體太擁擠現象，則朝伙伴Xj的方向前進一步，否則執行覓食行為(步驟5)。

步驟5 執行覓食行為。設人工魚當前狀態Xi，在感知范圍內隨機選取下一刻狀態的人工魚Xj，代入目標函數計算出Yj，如果Yj>Yi，向該方向移動一步；如果不滿足，且在需要嘗試次數try_number后仍然不滿足時，則更新公告板。

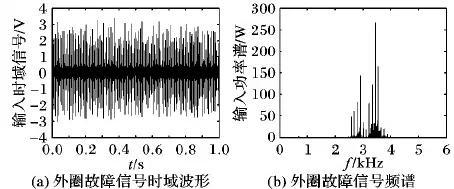
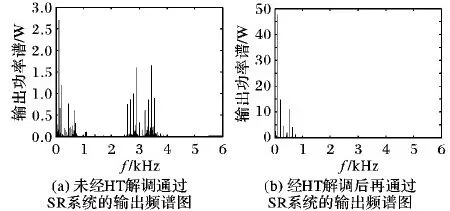
步驟6 若gen

步驟7 輸出公告板上的最優解，并記錄最優的目標函數相應的4個最優參數值。

3 系統仿真與應用

3.1 雙頻振動周期信號檢測

本文采用二倍頻的周期信號來驗證構造的冪指型周期函數能夠產生隨機共振并且比經典雙穩態系統的性能更優。這種構造多頻含噪的周期信號為：

s(t)=A1·sin(2π×ft)+A2·sin(2π×2ft)

(10)

其中：周期信號頻率f為10 Hz，周期信號的幅值為A1=A2=0.04，外加入噪聲強度為0.8的高斯白噪聲，由于采用的是大頻率的信號，所以依據二次采樣定律對大頻率進行預處理，采樣頻率fs=5 Hz， 二次采樣頻率fsr=5 000 Hz，采樣點數為10 000。預處理后信號分別通過冪指組合型三穩態系統和雙穩態隨機系統，雙穩態系統的參數常規設置(a,b)=(1,1)，而冪指組合型三穩態系統經過人工魚群尋優的參數為(a,b,V,R)=(5.575,2.889,4.643,1.323)。圖7(a)是含噪的信號時域波形圖，圖7(b)是含噪的頻域圖，而在頻域圖中特征頻率處不能夠明顯辨別出該頻率處的峰值，在10 Hz、20 Hz處峰值分別是5.835 W、7.4 W。原始微弱信號采用信噪比是-25.8 dB。通過二次采樣后，通過冪指型隨機共振后，如圖8所示，在頻域圖中特征頻率10 Hz,20 Hz處，分別為213.1 W、150.4 W。組合三穩系統輸出信噪比為-8.59 dB。如圖9，在頻域圖中特征頻率10 Hz,20 Hz點處，分別為178.4 W、30.64 W，雙穩系統輸出信噪比為-13.1 dB。說明在噪聲強度為0.81時，通過參數調節，組合三穩系統與雙穩系統相比，組合三穩系統的輸出信噪比提高了一倍多。系統性能通過信噪比增益來表征，如圖10所示。增加不同的輸出信噪比，系統性能信噪比在-30 dB附近是個拐點，信噪比大于-30 dB時，開始出現隨機共振現象。

圖7 原始的含噪多頻振動信號

圖8 組合型冪指函數三穩態隨機共振

圖9 雙穩態系統時域與頻域波形

圖10 冪指組合型三穩態系統輸入信噪比對系統輸出的影響

3.2 工程應用

滾動軸承故障信號是具有調制性、非平穩性的微弱信號，常常被強大的機械噪聲淹沒，利用本文新型系統模型的檢測系統對機械滾動軸承進行故障診斷，能夠檢測故障頻率，因此新型檢測系統具有良好的檢測性能。該實驗平臺采用Case Western Reserve University Bearing Data center[22]，選用的對象是6205-2RS JEM SKF的深溝球軸承，分別對外圈和內圈故障進行檢測。外圈故障的特征頻率為107.3 Hz,內圈故障的特征頻率為162.2 Hz；軸承轉速為r=1 796 r/min，采樣頻率為12 000 Hz，二次采樣頻率為5 Hz；外圈采樣點為12 000。

圖11是外圈原始信號時頻圖，通過智能算法尋優得到一組參數(a,b,V,R)=(3.141,3.962,5.228,1.915)和圖12，其中圖12(a)是經過未解調直接通過SR系統中輸出頻譜圖;圖(b)是經過解調預處理后，再通過SR系統中輸出頻譜圖。可以看出，通過解調后可以把原先高頻處的頻譜去掉，比較好地檢測出二倍頻。針對內圈故障檢測，所取采樣點為6 000，一組尋優參數為(a,b,V,R)=(2.557,3.752,2.343,1.336)。圖13是原始內圈故障的時域和頻域圖，經過智能算法尋優的參數調節后，得到如圖14所示檢測出的時域和頻譜圖，在162 Hz處功率譜為2.073 W，與檢測前的輸入功率譜相比，輸出頻譜功率提高了5倍。因此組合型三穩隨機共振系統應用于故障診斷中具有一定的檢測效果。

圖11 外圈故障信號

圖12 外圈故障頻譜對比

圖13 內圈故障信號

圖14 內圈經過SR系統輸出信號

4 結語

本文把經典雙穩勢函數和Gaussian Potential單勢阱勢函數組合成一種新型的冪指型的三穩勢函數，形成了新型的冪指型組合型三穩隨機共振系統。通過高斯白噪聲強度與系統輸出平均信噪比的變化規律，來驗證該冪指組合型系統能夠產生隨機共振現象；再通過人工魚群算法進行四個參數的尋優，找到能使得系統輸出最佳的平均信噪比；通過最佳四個參數檢測大頻率的諧波信號，對比雙穩系統，仿真結果顯示，新型的三穩系統通過對噪聲的利用率高于雙穩系統，即輸出平均信噪比高于雙穩系統；最后把新型的系統應用于故障診斷中對內外圈的故障進行診斷，對于內外圈故障檢測，經過隨機共振系統能檢測出故障頻率，使得高頻分量被濾除掉，進而達到了最佳的檢測效果。