基于機會信號的區塊模型的能效最優簇數的研究

劉東 熊召新

摘 要： 依據無線傳感網絡（WSNs）中WiFi、聲或可見光的機會信號，提出基于最優簇數的區塊模型（CML）。區塊模型為衰落模型，反映機會信號隨傳播距離的衰減變化。為了減少總體能耗，利用區塊模型的泰勒級數展開的不同階次計算最優簇數。最后利用移動手機、無線接入點、聲和光信號建立真實的實驗平臺，分析最優簇數。實驗數據表明，相比Exponential模型和對數Log模型，CML的能耗分別下降約6%和8%。此外，相比于WiFi和聲信號，可見光信號的能效提高近12%。

關鍵詞： 無線傳感網絡； 能效； 簇； 機會信號； 區塊模型； 最優簇數

中圖分類號： TN914?34 文獻標識碼： A 文章編號： 1004?373X（2018）19?0019?04

Abstract： A compartmental model based on optimal cluster number is proposed according to the opportunity signals of WiFi， acoustics and visible light in wireless sensor networks （WSNs）. The compartmental model acting as an attenuation model can reflect the attenuation variation of opportunistic signal with propagation distance. In order to minimize the overall energy consumption， the different orders expanded by the Taylor series of the compartmental model is used to calculate the optimal cluster number. The mobile phone， wireless access point， sound and light signals are adopted to establish the real experimental platform to analyze the optimal cluster number. The experimental data shows that the energy consumption of the compartmental model is reduced by about 6% and 8% respectively than that of the exponential model and logarithm model， and the energy efficiency of the visible light signal is improved by about 12% than that of the WiFi and acoustic signals.

Keywords： wireless sensor network； energy efficiency； cluster； opportunity signal； compartmental model； optimal cluster number

0 引 言

能效是許多通信系統的基本要求，如無線傳感網絡（Wireless Sensor Networks，WSNs）、物聯網（Internet of Things，IoT）[1]。為了解決高層問題，如定位、跟蹤、路由和連通問題，將興趣區域劃分不同的區。基于簇的拓撲結構是典型的分區技術。分簇技術充分利用了傳感節點的有限通信半徑。每個簇內產生一個簇頭，并由簇頭先融合數據，再向信宿傳輸這些融合數據[2]，數據傳輸示意圖如圖1所示。

低功耗自適應簇協議LEACH[3]，LEACH協議用Type?2邏輯算法選擇簇頭，簇頭在節點間輪流轉換，進而平衡網絡能耗。盡管簇技術能夠降低網絡能耗、提高數據傳輸效率，但是在固定網絡下，分多少個簇，即最優簇數仍是一個挑戰問題[4?5]。分簇的根本目的是減少能耗。因此，分簇必須與能耗相結合。為此，本文以最小化總體能耗為目標，進而優化最優簇數。

目前，所有簇技術是基于距離[dn]或指數無線能量消耗模型，其中[n]是路徑衰落指數。此外，文獻[6]針對WSNs的定位和跟蹤，提出有效的區塊（Compartmental）模型。在非視距環境下，相比于指數Exponential模型和對數Log模型[7]，Compartmental模型具有較好的性能。這激發了利用Compartmental模型優化簇數的動力，從而實現總體能量消耗的最小化。

此外，基于不同的應用，引用機會性信號是不錯的策略。機會性的信號，如WiFi、聲信號或可見光等。可依據不同的應用，選擇這些機會性信號進行分析。例如，可見光不適合室外場景；聲信號在安靜環境無法使用；WiFi信號在擁擠地方衰減迅速。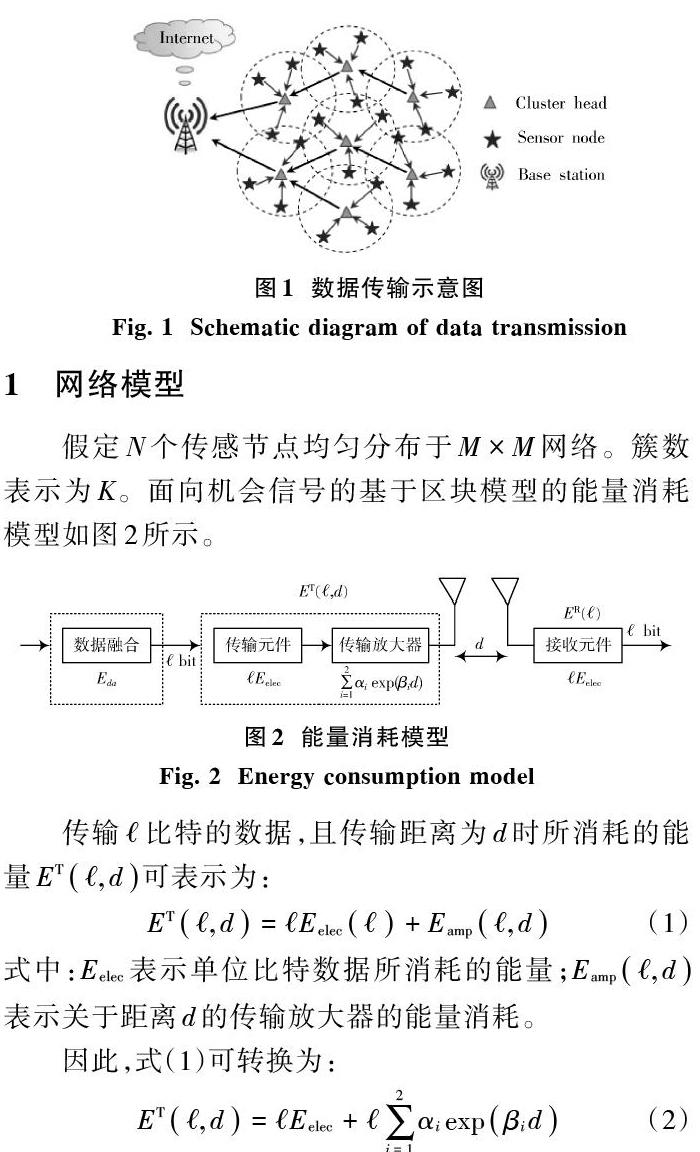

為此，提出基于機會信號的WSN最優簇數的研究。先建立基于最小能耗的Compartmental模型，然后利用泰勒級數展開算法分析在不同階次下的最優簇數，最后利用移動手機、無線接入點、聲和光信號建立真實的實驗平臺，分析最優簇數。實驗數據表明，基于Compartmental模型的平均能耗比Exponential模型和對數Log模型分別下降約6%和8%。

1 網絡模型

假定[N]個傳感節點均勻分布于[M×M]網絡。簇數表示為[K]。面向機會信號的基于區塊模型的能量消耗模型如圖2所示。

從上述分析可知，能耗與距離[d]成非線性關系。為此，利用泰勒級數展開[8]分析能耗與距離的關系。考慮到計算量，只分析低階次項。

1.1 一階項

可利用任意的求根法獲取式（13）的閉合解，如牛頓法、梯度下降法等。最終，可獲取簇數的最優解[Kfirstopt]。

1.2 二階項

2 性能分析

2.1 仿真平臺

在2.4 GHz頻段，將無線標準IEEE 802.11引用于接入點（Access Point，AP）與移動手機間的通信。接入點AP（TP?Link TL?WR841N）由2個全向天線組成，且其有5 dBi的增益。智能手機（Moto E3）測量室內多個位置的來自AP的信號強度。同時，分別利用安卓聲音檢測器、Lux Meter分別測量室內多個位置的聲、光信號，且分別采用852 Hz的單音頻和700 nm的單色光源。在室內每隔0.6 m收集這些機會信號。引用改進的Prony estimator[6，9]估計區塊模型的參數，如表1所示。此外，[Eelec=50] nJ/bit，[Eda=5] nJ/bit/signal，[?=]4 000 bits。

2.2 數據分析

2.2.1 不同能量模型的平均能耗

本小節分析不同能量模型的平均能耗性能。為此，引用文獻[6?7]所述的Exponential模型和對數Log模型作為參考。依據文獻[6?7]，指數、對數模型可分別表示為：[Eamp（d）=αexp（βd）]，[Eamp（d）=γlogd+δ]。實驗數據分別如表2和圖3所示。

從圖3可知，隨著簇數的增加，平均能耗也隨之增加。相比于Exponential和Log模型，本文提出的Compartmental模型的平均能耗得到了有效控制。對比圖3a）和圖3b）可知，節點數的增加加大了平均能耗。

表2列舉了這三個模型的最優簇數，并分別列出直接搜索和推導分析兩種策略下所獲取的最優簇數。從表2可知，相比于Exponential和Log模型，Compartmental模型能得到最優的簇數。同時，節點數的增加也提高了最優簇數。

2.2.2 不同信號模型下的平均能耗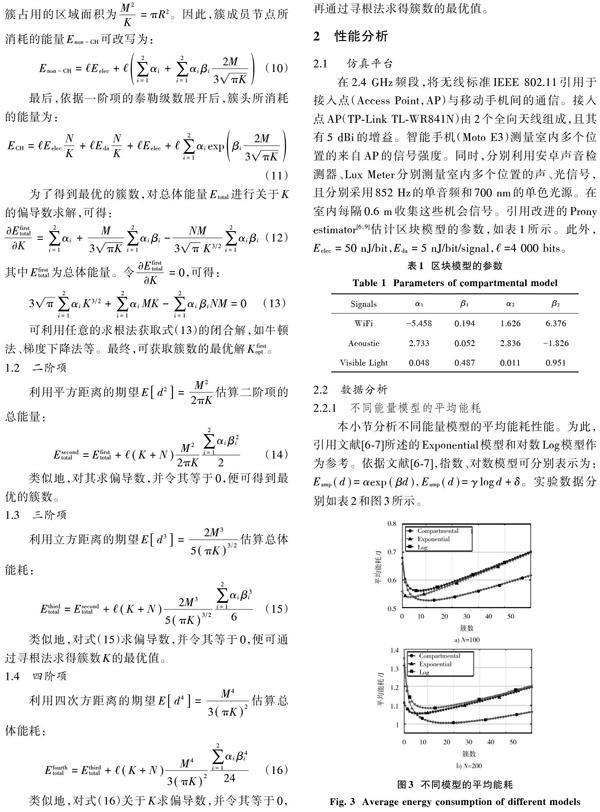

本節分析Compartmental模型在不同信號模型（WiFi、Acoustic、Visible light）下的能耗和最優簇數。實驗數據如圖4所示。

從圖4可知，在[N=200]時，與WiFi和Acoustic信號相比，可見光信號消耗的能量更少。原因在于：在高照度要求下，可見光信號具有高的信噪比。與其他信號相比，可見光信號隨傳輸距離的衰減變緩。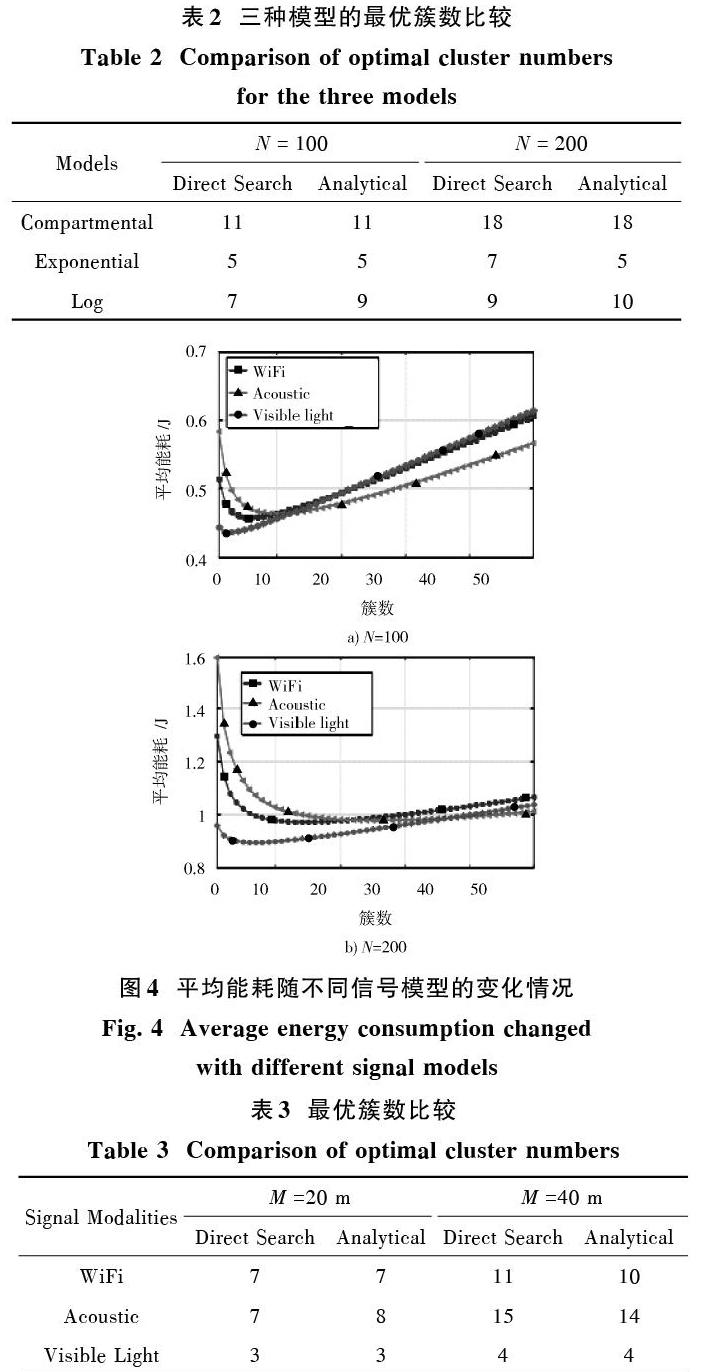

表3顯示了不同信號下的最優簇數。從表3可知，可見光信號下，簇數最少。此外，從表3不難發現，[M]的增加擴大了簇數。

3 結 語

本文針對無線傳感網絡的能耗問題，提出基于最優簇數的區塊模型。該模型利用WiFi、聲、可見光的機會信號，并引用泰勒級數展開，分析在不同階次下的最優簇數。實驗數據表明，利用基于可見光的區塊模型的能耗最低。與指數和對數的能耗模型相比，本文提出的區塊模型的平均能耗得到了有效控制。

參考文獻

[1] LENG M， TAY W P， SEE C M S， et al. Modified CRLB for cooperative geolocation of two devices using signals of opportunity [J]. IEEE transactions on wireless communications， 2014， 13（7）： 3636?3649.

[2] AMINI N， VAHDATPOUR A， XU W， et al. Cluster size optimization in sensor networks with decentralized cluster?based protocols [J]. Computer communications， 2012， 35（2）： 207?220.

[3] HEINZELMAN W B， CHANDRAKASAN A P， BALAKRISHNAN H. An application?specific protocol architecture for wireless microsensor networks [J]. IEEE transactions on wireless communications， 2002， 1（4）： 660?670.

[4] CUEVAS?MARTINEZ J C， YUSTE?DELGADO A J， TRIVINO?CABRERA A. Cluster head enhanced election type?2 fuzzy algorithm for wireless sensor networks [J]. IEEE communications letters， 2017， 21（9）： 2069?2072.

[5] YADAV S， KUMAR V. Optimal clustering in underwater wireless sensor networks： acoustic， EM and FSO communication compliant technique [J]. IEEE access， 2017， 5（12）： 12761?12776.

[6] KUMAR S， HEGDE R M. An efficient compartmental model for realtime node tracking over cognitive wireless sensor networks [J]. IEEE transactions on signal processing， 2015， 63（7）： 1712?1725.

[7] WANG G， CHEN H， LI Y， et al. On received?signal?strength based localization with unknown transmit power and path loss exponent [J]. IEEE wireless communications letters， 2012， 1（5）： 536?539.

[8] HARB H， MAKHOUL A， TAWBI S， et al. Comparison of different data aggregation techniques in distributed sensor networks [J]. IEEE access， 2017， 5（2）： 4250?4263.

[9] OSBORNE M R， SMYTH G K. A modified Prony algorithm for exponential function fitting [J]. SIAM journal on scientific computing， 1995， 16（1）： 119?138.

[10] KUMAR S. Compartmental modelling of opportunistic signals for energy efficient optimal clustering in WSN [J]. IEEE communications letters， 2017， 21（1）： 173?176.