面向空間在線分析的并行近似聚集查詢*

申金鑫，吳 燁，陳 犖，景 寧

國防科技大學 電子科學學院，長沙 410073

1 引言

信息化世界里，人人都是移動的數據“生產者”。隨著基于位置的服務普及以及各類移動定位設備的增長，空間數據呈現出“爆炸式”增長，例如，OpenStreetMap全球點矢量數據集已有超過27億條記錄。為從日趨海量化的數據中獲取有用信息，聚集查詢[1]方法呈現出越來越重要的作用。當前很多空間在線應用需要的是一個聚集結果，而不是單個對象信息的集合。例如，查詢北京市區某個立交橋區域在某一時刻的車流量，以便于檢測交通擁堵，并不需要查詢范圍里的所有車輛具體的信息。

聚集查詢具有數據密集和計算密集的特征，是一種耗時操作。空間索引是提升聚集查詢速度的有效手段。R樹是一種典型的二維空間索引，采用最小邊界矩形對空間進行劃分[2-5]。Ra*樹在傳統R樹的基礎上增加聚集信息，是最早的多維聚集結構，其目的在于有效處理窗口聚集查詢[6]。之后，聚集R樹（aggregation R-tree，aR樹）在R樹節點的最小外接矩形內標注了其所包含的所有對象的聚集值，在聚集計算時可直接引用該信息，不用對每個對象進行聚集計算[7]。隨后，很多空間聚集索引技術不斷深入發展[8-10]。

在線聚集應用中的需求可分為兩類：一類要獲取精確查詢結果；另一類只需近似結果。對于后一種需求，以犧牲結果精度為代價來減少等待時間，但是要保證查詢精度能夠隨著時間推移不斷提升，且隨用戶需求而停止。就現有研究成果而言，對第一種需求還沒有針對聚集索引的并行構建方法。對后一種需求，基于數據采樣的近似聚集大多非針對空間數據；同時，返回近似結果時，也不能保證精確查詢結果的速度。

最近，大數據處理架構飛速發展，為在線聚集查詢性能的提升帶來機遇和挑戰。機遇源于其高效可擴展的特點；挑戰就空間聚集查詢而言，包括數據劃分和任務分解兩個普遍問題。在數據劃分時，如何保持數據的空間鄰近聚集特征，處理常見的數據傾斜和邊界對象分配問題[11]。在任務分解時，如何分解數據分區，避免分區不均導致負載不均衡以及分區過多導致的大量初始化開銷。

本文將精確查詢和近似查詢兩種需求結合起來，在提升精確查詢效率的同時，又能在精確結果返回前快速反饋近似查詢結果。針對精確查詢需求提出了基于Hilbert空間填充曲線劃分的聚集網格R樹（Hilbert partition based aggregation grid-R tree，HAGR樹）。然后在此基礎上提出了一種多層級采樣聚集樹（multi-layer sampling aggregation R-tree，MSAR樹）。

本文的主要貢獻如下：

（1）對Hilbert-aR樹進行并行優化，在此基礎上實現了HAGR樹，通過Hilbert數據劃分提高了索引搜索效率，建立全局網格索引提升了并行查詢效率。

（2）基于金字塔和大數據隨機采樣思想，在并行HAGR樹的基礎上提出了MSAR樹，通過概率查詢的逐步求精方式進一步提升了聚集計算效率，并且能夠實現良好的交互。

（3）在10億規模真實數據集上，驗證本文方法的有效性和正確性，能夠返回給定置信度下的置信區間，實現漸進式聚集計算。

2 相關工作

當前，近似聚集方法可以分為預計算和在線聚集兩類[12]。本文關注其中后一種方法。而在線聚集方法可進一步分為非索引的在線聚集方法[13-15]和基于索引的在線聚集方法[16-17]。

在非索引的在線聚集方法方面，在線聚集（online aggregation，OA）是一種在線近似聚集方法，不斷從底層隨機獲取元組并統計，然后在3個準則基礎上計算置信區間，直到結果滿足用戶的要求[13]。DBO數據庫原型系統能實現近似聚集查詢，很快返回一個推測結果，隨時間推移，各種關系操作從互相通信中獲取更多滿足條件的元組，因而推測結果的精度也隨之越來越高[14]。基于分塊的近似聚集算法（partition-based approximate aggregation，PAA）是一種基于劃分的近似聚集方法，對數據預先構建一個隨機樣本。在查詢時，首先在預構建的樣本中查詢，如不能滿足要求，再從與查詢區域相交的各個分片集合中獲取更多元組[15]。

在基于索引的在線聚集方面。MRA樹是一種多粒度聚集樹，該樹的每個葉子節點與一個區域范圍相關聯，存儲其孩子節點的聚集信息。在查詢時，判斷節點空間范圍與查詢范圍的空間位置關系，以此來決定是否查詢該節點的子節點。將該思想與四叉樹（MRA四叉樹）和R樹（MRA-R樹）結合，提供漸進的估計結果以及100%置信度的置信區間[16]。LS樹和RS樹這兩種索引方式是專門針對空間和時空在線分析提出的，在查詢過程中不斷獲取新的采樣樣本，采樣實現了一種面向在線空間或時空分析的逐步求精的查詢方式，能在任意置信度下反饋估計結果以及置信區間[17]。

以上方法往往在單機中進行，為提升聚集計算效率，一系列并行改進逐漸出現。基于MapReduce計算模型，能夠在查詢執行期間以順序流傳輸數據，進而不斷修正結果[18]。基于數據庫和大規模分布式節點方法，可以設計采樣創建和采樣選擇策略，以多層采樣方式實現對給定的誤差或是給定時間這兩種查詢模式[19]。這些方法都在大規模數據上取得了良好的效果，但是這些方法都不是專門針對空間數據而設計的。

在并行空間計算方面，基于MapReduce和Spark計算模型，已經有Hadoop-GIS[11]、SpatialHadoop[20]，以及GeoSpark[21-22]、SpatialSpark[23]、LocationSpark[24]、Simba[25]等系統，提供了格網、四叉樹、R樹等空間索引支持來加速空間查詢等操作，其中大多系統支持R樹的并行構建[11,20-21,24-25]，然而并不提供空間聚集索引的構建。

基于以上分析，現有的概率聚集方法很少應用于空間數據，且現有的空間分析系統并不支持聚集索引。因此，為了提升面向空間大規模數據的聚集分析，本文基于分布式內存計算架構Spark，針對在線聚集查詢應用，提出了兩種索引方式，HAGR樹和MSAR樹。其中，HAGR樹支持快速時空精確聚集分析計算，MSAR樹結合概率聚集查詢，進一步增強了在線時空聚集查詢的交互性。

3 問題描述

給定空間數據D，其中的元組可表示為K,V鍵值對的形式。其中K(K1,K2,…,Kd)表示元組的d維屬性信息，例如，空間矢量數據中d=2。V(V1,V2,…,Vv)表示元組的值屬性信息，對空間數據而言，V是包含各種空間屬性信息的集合，例如：(Oid,Geometry,…,Geometry Type)等。

聚集查詢可表示為F=fagg(op(V|Q?QR))。其中QR表示查詢區域；fagg表示聚集函數，包含SUM、AVG、COUNT、MIN以及MAX等常見聚集函數操作；op表示屬性操作，代表一般操作映射函數；Q是D的范圍，則Q?QR表示相交區域。

對于在線近似聚集，僅當聚集結果來自隨機采樣中獲得的元組，得到的結果才是有統計意義的估計結果。這一要求可以通過Heap Scans、Index Scans、Sampling from Indices方法保證，避免元組的屬性值影響其檢索的順序[13]。滿足上述條件基礎上，近似聚集查詢還需要其他衡量指標，包括置信區間CI，置信度p∈(0,1)，以及誤差范圍ε。誤差范圍即置信區間寬度，是對估計精度的度量。得到這些指標后，即可通過公式CI=為用戶終止查詢提供判斷。

4 并行聚集查詢索引

本文對aR樹并行優化，與Hilbert編碼的數據劃分方法結合。在HAGR樹構建過程中考慮數據劃分和任務分解兩個優化問題，處理了數據劃分過程中常見的數據傾斜和邊界對象問題，在查詢中提供了一種基于空間關系判斷的深度優先搜索（depth first search，DFS）方法。

4.1 HAGR樹構建

HAGR樹構建首要考慮是并行環境中高效構建，因而需要合理的數據劃分和任務分解作支撐。為展示數據構成，因而又將D表示為D={di|i∈[1,N]}，d為單個元組，N為元組總數。

Hilbert編碼劃分方法。采用Hilbert編碼的劃分后，可以獲得幾乎近100%的空間利用率。因而，構建的Hilbert-R樹的查詢性能優于平方復雜度節點分裂的R樹、R*樹和Roussopoulos的批建立方法[26]。根據Faloutsos等[27]提出的Hilbert曲線編碼生成算法，目標點的Hilbert編碼值計算復雜度為，其中nh是空間層次劃分次數，即該點所在網格行列中數較大值所對應的二進制位數。

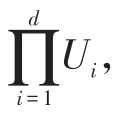
并行計算中，網格索引能實現高效關系判定，以實現有效剪枝。因而，本文在結合網格和聚集R樹索引后得到一種兩級索引——HAGR樹。其構建過程如圖1所示，主要分為數據劃分、數據排序、數據分解以及并行索引構建等4個步驟。

（2）在此基礎上，按照Hc對數據集排序，實現空間聚集特性。

（4）以D1D2…Dk為基礎并行構建Local Index，得到tree1tree2…treek。如圖1右下角，tree中A1區域的聚集結果直接由子節點a1+a2+a3獲得。之后，獲取各個數據塊的Mbb，更新Global Index，完成兩級索引構建。

4.2 數據傾斜和邊界對象處理

并行計算數據劃分過程，數據傾斜和邊界對象這兩個問題不可避免。數據傾斜源于實際數據的空間維度分布不均，會影響計算效率。例如，同一個Hc可能對應了多條元組，這些元組空間上無序，無法增加聚集特性，且在后續任務分解中容易造成分解不均。邊界對象源于網格劃分方式，若處理不好可能導致查詢結果錯誤。

數據傾斜處理。在HAGR樹構建的第（1）步中，添加處理算法。對輸入數據采樣，減少后續處理計算I/O；然后統計每個T包含的數據量TNH，定義閾值參數Cmax，如果存在TNH>Cmax，將Hilbert曲線編碼的劃分密度增加一倍；重復以上操作直至滿足要求。

邊界數據處理。對這類跨越邊界的數據，有指定網格和復制方法[11]。考慮到實際點矢量數據跨越網格的情況并不多見，本文采用了指定網格法。

Fig.1 HAGR-tree construction圖1 HAGR樹構建流程

4.3 查詢算法

索引構建完成后，采取一種基于空間關系判斷的迭代式深度優先查詢方式。空間關系判斷在兩層索引的查詢過程中都有涉及。

空間關系判斷。本文中，將空間關系主要分為4類：包含、相交、外包以及不相交。以Local index中給定QR的查詢LIQ（local index query），P為一個節點，Pi是一個指向根節點的指針，P.agg是節點對應的聚集值，P.Mbb是節點對應的外包框，P.child是子節點。則4種關系描述如下。

（1）包含，Mbb∈QR，可以直接從該節點獲取聚集值P.agg。

（2）相交，QR?Mbb≠ ? 且QR?Mbb≠QR，需要繼續查詢P的所有孩子節點。

（3）外包，QR?Mbb=QR，同樣需要繼續查詢孩子節點。

（4）不相交，QR?Mbb=? ，該節點及其孩子節點直接出隊，不再查找。

綜合得到查詢過程如算法1所示。首先利用Global Index實現剪枝，然后利用LIQ進行一種迭代式的DFS查詢，過程中判斷QR與該節點的Mbb的空間關系再繼續查找，直到獲得所有Local Index的結果，合并后輸出最終的Ra。

算法1HACR樹查詢算法

輸入：HAGR樹H-tree，聚集范圍查詢QR。

輸出：聚集查詢結果Ra。

1.search inGlobal Index,find everyMbb?QR≠ ? ；

2.for each qualifiedMbbdoLIQ(Pi,QR)；

3.collect the answer,print the finalRa.

4.FunctionLIQ(Pi,QR){

5.for each branchP∈Pi

6.ifQRcontainsP.Mbb{Ra+=P.agg;}

7. else ifQRintersectsP.Mbb

8. caseP.childis branch

9. for eachP.childdoLIQ(P.child,QR);

10.caseP.childis leaf

11. for everyP.child

12. ifQRcontainsP.child{Ra+=1;}

13. end for

14.end if

15.end for}

5 面向在線交互的索引方法

基于HAGR樹索引，能夠并行反饋精確聚集查詢結果，但是在線應用中，有時用戶并不愿為精確的查詢結果等待長時間。如果隨著時間推移，查詢結果的精度越來越高，且用戶能在任意時間結束該查詢，這將能大大提升在線查詢的交互性。基于此，本文提出了MSAR樹，給出了近似分析的基本思想和理論支撐，介紹了構建流程以及查詢方法。

5.1 隨機采樣和聚集

MSAR基于數據采樣、金字塔構建以及逐層求精3種思想。此外，構建的隨機樣本滿足獨立同分布，這樣后續的分析才有統計上的實際意義。

數據采樣。采樣是應對大規模數據的一種有效手段，降低了后續處理的I/O。PAA[15]中維護固定大小為M∈[10，100]的RS（M單位為MB），在處理356 GB的數據時，M=25 MB，S=0.0686%，且RS緩存到內存中，因而實現了很高的查詢效率。本文設定采樣率S(S∈(0,1))，并不固定樣本的大小，而是采用一種無放回的采樣方式構建動態隨機樣本集DS（data of random sample）。

逐層查詢求精。數據量小的數據查詢速度較快，因而從最高層級Layerl開始查詢，根據用戶的反饋決定是否終止查詢。

以上思想需要隨機采樣理論作為支撐，而這方面已有很多相關研究[13,28-30]。Haas對范圍查詢的采樣方式使用了新的約束，樣本在查詢內部和查詢之間必須是獨立的，這樣的方法很好地實現了理論上的完備性。但是在實際應用中，尤其是面向超大規模的空間數據，耗費比較多的時間[30]。在OA[13]研究中，使用中心極限定理來計算近似聚集查詢結果，這要求使用的數據必須是隨機獲得的。本文中，先獲取DS，采樣得到的數據即為隨機元組集合。然后，對DS基于索引聚集查詢。根據Index Scans，這是具有實際統計意義的結果。

近似分析時需要數據滿足獨立同分布，后續分析才有統計意義。本文認為這樣得到的元組信息是滿足獨立同分布。基于以下三點認識：

（1）對不同用戶而言，一般他們只會執行相同的QR一次。即便進行多次，只要等待（結束查詢）的時間不一樣，得到的Ra不同。

（2）索引更新代價并不高，對于實際中產生的數據采用實時采樣更新的方式添加，這樣更新前后的數據是有差異的。

（3）為了應對上億規模或是更大的空間數據集D，相應的預處理過程是很有必要的。

5.2 MSAR樹構建

在時空數據采樣的基礎上，得到了金字塔多級數據，然后以此為基礎進行索引構建。LS樹采用類似的思想實現了多層級索引，在單機環境中實現[16]。為了在分布式環境中應用，充分優化提升索引效率，本文提出的MSAR樹還有以下特點。

自適應數據分塊。數據金字塔中，各個層級Ni（i∈[1，l]）差異較大，因而須根據Ni進行不同粒度的數據分解。當層級低，Ni大的時候，分塊盡可能多，ki≥3c；當層級高，Ni小的時候，分塊相應減少，因為過多分塊會導致很多初始化開銷。

并發并行查詢。為了獲取近似結果的同時快速獲取精確結果，本文還可采取并發方式，對多層級索引同時查詢，為在線聚集查詢提供更佳體驗。

MSAR樹的構建過程如圖2所示，可分為隨機樣本獲取、劃分及分塊、索引構建3個主要步驟。

Fig.2 MSAR-tree construction圖2 MSAR樹構建流程

（1）隨機樣本獲取。設定S，構建數據金字塔DS0DS1…DSl。

（2）劃分及分塊。在各個DS基礎上得到輸入數據Data，進行數據劃分、數據排序；然后處理數據傾斜和邊界對象；最后自適應數據分塊。

（3）索引構建。在各個層級上建立Local Index和Global Index，并依據硬件條件動態緩存，得到MSAR樹。

5.3 查詢算法

在查詢時，基本方法如算法2描述所示，LIQ與算法1同，輸入為整個Local Index。具體查詢過程中，既可以按照高層級到低層級的方式進行，還可以進行并發查詢。算法中描述的是順序查詢方法。

算法2MSAR樹查詢算法

輸入：MSAR樹M-tree，聚集范圍查詢QR。

輸出：聚集查詢結果Ra。

1.whileLayer>0,do{

2.search inGlobal Index,find everyMbb?Q≠? ;

3.for every qualifiedMbbdo

4.LIQ(Local Index,QR);

5.returnRaandCI

6.ifRais qualified

7.exit query

8.else

9.Layer=Layer-1

10.end if}

6 時空在線分析與估計

6.1 估計總體查詢結果

對MSAR樹，除底層數據外，其他層級的數據都是隨機采樣所得到的。范圍查詢QR數據分互斥的元組集合：滿足QR的集合，不滿足QR的集合。

結合OA方法，本文基于索引聚集查詢，得到的是具有實際統計意義的結果，因為用于構建索引V不同于用來聚集計算的V，避免了數據屬性值影響其檢索的順序。

6.2 置信區間計算

MSAR樹反饋的近似結果需要一個評價指標，使得用戶能夠根據結果做出是否采納當前結果的判斷。而且，在保證置信度水平不變的情況下，需要盡可能縮短CI的寬度，提高結果質量。由于本文針對大規模空間數據進行分析，可以由CCI（conservative CI）和LCI（large-sample CI）分析，但是選擇了后者作為衡量標準，因為LCI較CCI往往能提供更短的CI。

在對整體估計基礎上，根據Hoeffding不等式即可以計算出CCI，結果區間為[Yn-εn,Yn+εn]，能夠保證最終結果大于或等于p。

7 實驗

7.1 實驗設置

本節評價兩種索引方法的性能。程序利用Scala語言實現，Spark版本為1.6.1，Hadoop版本為2.6.3，Scala版本為2.10.4。具體機器配置如表1所示。

Table 1 Experiment environment表1 實驗環境

本文使用OpenStreetMap線矢量數據中的節點作為點數據，如表2所示。其中，OSM_China（OP）表示中國區域的數據，OSM_Planet（OP）表示全球數據。實驗中，選取GeoSpark[21]中的R樹索引（GR）和Simba[25]中的R樹索引（SR）與本文算法進行比較。實驗從索引構建時間、查詢效率、誤差和置信區間四方面評價不同算法。

Table 2 Experimental datasets表2 實驗使用的數據集

7.2 索引構建時間比較

本實驗首先評價HAGR樹和MSAR樹在單機、集群環境下的構建效率。

Fig.3 Performance comparison on index construction圖3 索引構建性能比較

單機構建時間比較。如圖3（a）所示，GR樹的構建速度最快，因為其針對空間數據結構在每個分區內構建局部索引，以一種自適應方式根據數據塊大小決定是否構建索引。HAGR樹構建速度較SR樹稍快，差別并不大，但兩者較GR樹的構建時間慢一個數量級，且這一趨勢隨著數據量增加愈發明顯。由于數據采樣、多層級索引構建及緩存等，MSAR樹構建最耗時，大致為HAGR樹的兩倍。

集群構建時間比較。結果如圖3（b）所示，應對16.9億條數據時，GR樹構建時間為80.3 s；MSAR樹構建時間是465.5 s，都能較快完成。（a）（b）中的數據不同，OP是整個地球的數據集，其范圍較OC廣得多，構建更復雜。即便如此，兩者同樣規模的數據對比依舊具有一定分析意義。在N為5000萬時，HAGR、MSAR和SR比單機快，因為合理的數據劃分和并行構建。而GR提升效果不明顯，尤其是當數據量小的時候，這正是由于其特定數據劃分以及自適應構建方式導致的。總體而言，本文方法在集群具有較好可擴展性。

7.3 查詢時間比較

本實驗比較在查詢過程數據大小N變化、固定查詢框的比例QR/Q，以及查詢框的比例QR/Q變化、固定數據集N這兩種情況下，查詢時間的變化。MSAR樹反饋的是最高層級（l=10，S=50%）的查詢結果。將l10層級采樣數據量視作PAA[15]中的RS，并行進行順序元組查詢方法即可視作并行PAA方法中階段一的查詢，這一階段查詢僅僅利用預構建樣本查詢，以P-PAA（parallel PAA）表示。P-PAA僅僅應用在QR/Q變化，固定N的實驗中，因為該方式下固定數據集大小，更接近原文中階段1的查詢方法。

（1）N變化，固定QR/Q

Fig.4 Performance comparison on index query圖4 索引查詢性能比較

單機實驗。結果如圖4（a）所示，由于3種優化措施，MSAR樹查詢性能最優。在N為5000萬時，MSAR相較于HAGR、SR以及GR分別實現了2.8、17.5、199.9倍的性能提升。HAGR樹的查詢性能相較于SR樹大致提升一個數量級，且隨N增加而更加明顯。這是因為全局網格索引實現有效剪枝，當N增加時元組密度增加，單個D的Mbb會減小，因而相同的范圍中包含了更多的完整數據塊，這些數據塊的聚集結果可以直接在全局索引中獲取。然而，構建速度最快的GR樹查詢效果卻最慢，這是由于GR樹僅僅構建了局部索引，其中自適應的方式沒對較小的數據塊構建索引。

集群實驗。如圖4（b），集群環境中進行同樣的實驗得到了基本類似的結果，4種方法都能夠應對16.9億規模數據。MSAR樹實現了更高的穩定性。但是應對同等N的數據集時，MSAR、HAGR和SR都并未表現出提升，這是由于數據的空間范圍大大增加，提升了查詢復雜度。GR的提升是由于該數據集上更合理的劃分方法。

（2）QR/Q變化，固定N

對于特定數據集，當查詢框的面積變化時查詢性能的變化。在該實驗中，添加了兩種比較方法，RR（range report）和P-PAA。RR是并行遍歷方法，對非采樣數據進行查找。

單機并行環境。如圖4（c）所示，即便并行進行，RR的查詢效率依舊較低。這種遍歷式的方法對資源消耗較大，不適用于在線交互。P-PAA并行遍歷RS后，僅僅耗時635.8 ms就能得到計算結果，耗時較GR短。MSAR樹、HAGR樹以及GR樹的查詢效率在QR增加時均呈現下降趨勢，這是由于前兩種方法在QR增加時可能覆蓋很多完整D的Mbb，因而不需要搜索Local Index便能得到聚集結果。類似的是，GR樹雖然沒有全局索引，但每個D包含整個數據塊的聚集信息，因而也會出現先上升后下降的趨勢。SR樹呈現上升趨勢，因為單個局部索引中不包含任何D的聚集信息，需要進一步查詢得到聚集結果。

集群并行環境。如圖4（d），實驗結果基本類似，HAGR樹和MSAR樹的查詢性能保持穩定。P-PAA的優勢更加明顯，平均僅需1112.8 ms就能得到計算結果。但是，GR樹的查詢時間隨QR先下降后上升，因為當數據量增加后，I/O和整體計算量依舊增加。

7.4 估計精確查詢結果

本實驗利用MSAR樹在OC上驗證，在單機并行環境中進行，采取由高層級到低層級的順序逐層反饋方式。

實際查詢結果如表3所示，其中Time為累計時間，Count為該層級的聚集結果，Error為相較于完整數據查詢結果得到的誤差。查詢時，按照從Layer10到Layer1的順序。當由Layer4查詢到Layer3時，Time迅速增加，這正是由動態緩存方式所導致的，Layer10到Layer4的數據都緩存在內存中，而剩余部分的數據都是緩存在磁盤中，因而查詢需要耗費更多時間。當查詢到Layer3時，查詢誤差已經下降到0.31%，達到了較高的精度。且從總體看來，誤差呈現下降趨勢。

Table 3 Result estimation and error analysis表3 結果估計及誤差分析

7.5 置信區間分析

本實驗估計近似查詢的效果。在面向在線分析的應用中，對用戶提交的查詢QR，及其設置的置信度p，為反饋的結果添加CI。

如圖5所示，利用與7.4節相同的實驗環境，設定p=95%，得到CI結果，由于估計結果兩邊的ε相同，因而未列出估計結果值。由圖可知，區間寬度逐漸收窄，即在同樣的置信度下精度不斷提升，估計效果越來越好。

8 結束語

Fig.5 Confidence intervals calculation圖5 計算置信區間

本文針對空間在線分析，從并行索引構建與查詢出發提出了HAGR樹和MSAR樹這兩種索引方式。前者能快速反饋精確聚集查詢結果，后者適用于漸進式近似聚集查詢，為解決空間大數據分析提供了兩種互為輔助的可行方案。通過10億級數據的實驗驗證了本文方法是可行、高效、可擴展的。