威布爾分布在面向服務的再制造回收決策中的應用

張 丹，蔡宗琰，劉清濤

（長安大學 工程機械學院，西安 710061）

0 引言

人類文明發展以來，對地球資源的消耗已經超出其恢復能力，大力發展經濟的同時要遵循科學發展理念，可持續發展是我國科學發展理念之一，要求發展必須以不損害后代人利益為代價，一方面達到發展經濟的目的，另一方面保護好人們賴以生存的地球。為了緩解資源消耗的速度與人類發展之間的矛盾，最大限度挖掘產品剩余價值，二十世紀九十年代，美國率先提出再制造這一概念，經過多年的發展已經具備一套完整體系。中國再制造起步較晚但發展迅速。

在傳統的再制造廢舊設備回收模式下，廢舊品的回收都是在設備完全報廢之后進行，也是目前主流回收模式。在設備完全報廢后回收的廢舊品，質量參差不齊，用于廢舊品再制造的加工工藝也不相同，而產品服役期間，在達到預定的再制造時間點，無論設備在該時刻狀態如何，都進行回收，那么用于再制造的廢舊品質量得到了保證，并且制造工藝路線也變的簡單。因此，定期回收再制造受到學者以及企業的關注[1]。

柯慶鏑[2]、宋守許[3]等就再制造廢舊設備最佳回收時期問題，提出了主動再制造理論，并分析對比了傳統再制造模式與主動再制造模式的相同與不同之處，得到了適用于主動再制造理論的最佳回收時機，主要零部件優先和可成批性。利用建立服役時間冗余強因子，壽命匹配等方面在產品設計初始通過零部件層和結構層的優化降低零部件的不確定性，再通過服役時間冗余強因子，壽命匹配等確定設備回收的最佳時機。

1 面向服務的再制造

1.1 面向服務的再制造含義

全球經濟飛速發展，競爭日益變得激烈，產品越來越向服務經濟過度，企業也從傳統的以產品為核心演變為以產品和服務為重點的新型模式，傳統制造業在時代變革的驅使下也從單一的制造加工價值鏈向制造加工與服務的綜合模式延伸，制造業與服務業越來越融合，越來越相互依存，服務的戰略意義及其占企業收益比重也逐步增加。

在傳統再制造模型基礎上，將原來制造業處于中游的產業鏈擴展至上游與下游，形成一條涵蓋了上、中、下的整體產業鏈。圖1所示為文章描述的這一模型。該模式使設備在設計初始就面向再制造設計，讓其更易拆卸，替換與裝配，使再制造變的簡單，整個價值鏈上游價值增加。通過回收，為客戶定制全壽命周期內解決方案，優秀的售后服務可使再制造品的營銷戰略更加成功，實現了整個價值鏈下游價值增加。整個過程中，客戶全程參與，可將信息，建議以及意見向企業反饋，企業與客戶之間的互動使服務價值增加[4]。

圖1 面向服務的再制造模型

1.2 面向服務的再制造特點

1）回收時機最佳：設備服役期間，其運行規律大致符合浴盆曲線，服役前段處于磨合期需調試，失效率較高，但此時間段內維修簡單，成本低廉；磨合期結束后為設備平穩運行階段，此階段偶發故障多由于人工操作失誤，維修較為容易；到了曲線第三階段損耗期，該階段維修頻次與維修成本上升。因此在設備進入第三階段且沒有徹底報廢之前確定回收時機，回收再制造，可將企業成本控制在最低。

2）批量回收：傳統再制造回收模型在設備報廢之后進行回收，由于回收渠道不同，回收行為不規范，回收的廢舊設備質量各不相同，這也使后續再制造工藝路線有所差別，一系列問題導致再制造生產無法批量進行。而在面向服務的再制造模式下，設備回收在徹底報廢之前，在確定最佳回收時機后，同批次設備處于正常運行狀態，損壞程度近似，在此時回收，再制造工藝路線基本相同，實現了再制造批量生產[2～4]。

3）服務優先：面向服務的再制造模式為客戶給與全壽命周期的解決方案，將關注點放在服務上，而不僅僅是產品自身，在客戶的溝通互動過程中實現共贏[5～7]。

2 面向服務的再制造最佳時機預測

面向服務的再制造模式的其中特征之一便是時機最佳性，在什么時機進行廢舊設備回收十分關鍵，如果回收過早，設備的原始價值沒有被利用完全，回收的過晚，設備損耗嚴重，回收難度增加，這就違背了可批量性生產的原則，造成資源損失。因此確定最佳回收時機至關重要。

2.1 模型假設

前文中提到機電設備的服役曲線符合浴盆曲線，在設備服役前期，設備處于磨合期，需要調試，雖然故障率高，但是維修簡單，成本較低；在進入浴盆曲線的第二階段，故障率上升，此階段的損壞多數由于人為操作不當造成，維修頻率低，維修成本低，在進入浴盆曲線第三階段，設備故障率迅速上升，此階段由于設備長時間磨損，銹蝕，疲勞等原因，維修頻率與維修成本快速上升，文章決策模型中考慮從浴盆曲線第三階段研究[8]。

2.2 威布爾分布

威布爾是連續型分布函數模型，它廣泛應用于設備和零部件的壽命預測，可靠性分析等。它先大致給定可靠度下零部件損耗開始時間Tb，但這并不是最佳回收時間，這一時間點處于浴盆曲線第三階段，可靠度符合要求，而在這一階段零部件出現一定程度的損耗，并經過多次維修，無法斷定是否能夠通過再制造使其恢復初始性能，而傳統再制造模式在此時進行回收。因此回收最佳時間的確定及其重要[9]。

文章提出只考慮產品的浴盆曲線第三階段的維修成本，另外，設備初始價值與再制造成本是設備在原始壽命周期服役的成本組合。

因此，目標設備在原始壽命周期內單位服役年限的成本最小值：

上式中：

D0為產品的原始價值；

Dr為再制造成本系數；

Dm為維修成本期望值；

M(t)為累計失效次數；

SD(tb)為優化目標；

tb為決策變量，即再制造時機，

t3為浴盆曲線的第三階段起點。

式中：

g(s)為產品的失效概率函數，可由威布爾擬合失效數據確定[10]。

三參數威布爾分布模型在結構與參數選取上都較為困難，實踐中通過優化后的兩參威布爾分布模型應用較為廣泛，兩參威布爾分布累計失效與概率密度函數如下：

兩參威布爾故障率函數：

將式(4)代入式(1)中，文章使用數值逼近方法求解目標值。

2.3 參數估計

現階段用以擬合威布爾分布參數有幾種方法，使用極大似然估計法過程繁瑣，圖估計法情況類似，因此這兩種方法不常使用，而最小二乘法由于操作簡單，精度準確等有點，文章采用該方法來擬合威布爾分布參數。

使用最小二乘法對參數進行估計時，因先估計該產品的累計失效概率，累計分布函數的準確性在一定程度上影響參數估計精確與否。經驗分析法是實踐中常用的累計失效概率方法：即利用經驗公式從維修時間序列里計算得出各個維修時間的累計失效分布函數值。（t1，t2，…，tn)，文章使用中位秩方法預估ti時刻累計失效分布函數F(ti)的預估值：

其中，i為失效順序；n是樣本值[11]。

累計失效概率預估是建立在采集來的數據樣本之上，失效數據充分體現了設備以及零部件在運行過程內的壽命演化，以此作為參數預估樣本比較理想。數據收集渠道主要有產品的實驗結果數據和收集的現場數據，實驗數據涵蓋了整臺設備及其零部件的數據。建立在失效數據基礎上，利用中位秩法以及最小二乘法進行兩參威布爾分布的數值預估，步驟如下：

兩參威布爾的可靠度表達式：

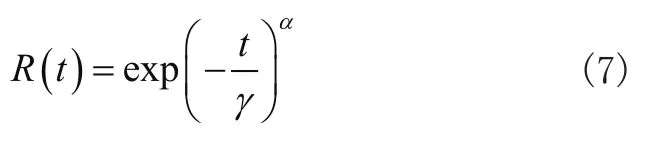
將失效率和可靠度關系式：

代入式(5)中，在對代入后的式子取對數兩次之后將其簡化成直線方程：

得到：

繼續進行取對數操作：

將式(11)進行變形，使其成為y=ax+b的形式，最小二乘法預估參數的中心思想是令想求解的值與實際值兩者間誤差平方和最小，從而得出數據最優函數匹配，計算式如下：

結合式(12)，先得到威布爾分布的兩個參數數值和失效分布函數，再聯合式(1)和式(2)，利用MATLAB優化工具箱函數得到再制造最佳時機[12,13]。

3 實例驗證

文章選取徐工XE80A型挖掘機作為研究對象。表1為驗證對象失效數據。該型號挖掘機使用的發動機總成30000元，令再制造成本系數為10000元，柴油機進入浴盆曲線的第三階段，維修成本期望為3000元，利用算例仿真分析證明文章提出的決策模型在面向服務的再制造時機預測中的應用。

依據以上數據，利用最小二乘法得到威布爾分布形狀與尺度參數是7.3788，14451.7。將得到的數據帶入決策模型，通過MATLAB求解，得到再制造最優時機為14782小時，以每年298天，每天運行7小時，挖掘機在7.08年后進行回收合理。

4 結論

文章針對機械設備的失效規律符合浴盆曲線，提出了一種新型的再制造模式，即面向服務的再制造模式，分析設備應在浴盆曲線進入第三階段后開始回收工作，以設備單位時間內運行成本最小作為求解目標，利用兩參數威布爾分布擬合失效函數。得到設備單位時間內成本最優的最佳回收時刻，并通過實例來驗證文章所提出的模型，證明了所建立模型的可行性。

表1 實例失效數據