高二學生科學推理能力現狀調查

李夢宇 李建彬 胡象嶺

(曲阜師范大學物理學系,山東 曲阜 273165)

1 引言

科學思維是指具有意識的人腦對科學事物的本質屬性、內在規律及事物間的相互聯系和關系的間接與概括的反映,是物理核心素養的構成要素之一．[1]科學推理(scientific reasoning)指的是個體對一個多變量系統進行推斷時表現出的思維能力,[2]是科學思維的重要組成部分．因此,開展關于科學推理能力的研究,是發展學生核心素養的必然要求．

科學推理能力水平的測量是科學推理能力研究的一項基礎性的工作．關于科學推理能力測量的工具有很多,例如美國學者Lawson編制的科學推理能力測試卷[3](Lawson’s Classroom Test of Scientific Reasoning,簡稱“LCTSR”,作者于2000年對該問卷進行了修訂,修訂版簡稱“LCTSR 2000”)．該測試卷在教育研究中有著廣泛的應用,如包雷等[4-6]利用該測試卷比較了中美大學生科學推理能力的發展水平,郭玉英等[7,8]研究了我國學生科學推理能力隨年級發展的規律．高中階段是學生發展的關鍵時期,研究該階段學生的科學推理能力的發展水平并基于此開展教學有助于學生的發展．但目前針對高中學生科學推理能力的研究卻比較少．為此,本研究擬使用LCTSR 2000測試卷,測量高中階段學生的科學推理能力發展狀況,以期為相關研究提供參考．

2 研究方法

2.1 測量工具

LCTSR 2000測試卷共有24道試題,測量了6個維度的科學推理能力,分別是質量與體積守恒推理(Reasoning of conservation of mass and volume)(簡稱“守恒推理”)、比例推理(Proportional reasoning)、控制變量推理(Control variable reasoning)、概率推理(Probabilistic reasoning)、相關推理(Correlation reasoning)以及假設演繹推理(Hypothetical-deductive reasoning)．測試卷的題目分布見表1．

表1 LCTSR 2000測試卷的題目分布

測試卷的24道題目均為有多個選項的單選題,每2道題目為一組,共描述了12個問題情境．每組題目中,前一道題目提出問題,后一道題目要求被試回答原因．本研究采用獨立計分法進行計分,即被試每答對一題計1分,答錯計0分,測試卷的總分為24分．

2.2 研究樣本

高二年級是學生的思維認知發展趨于成熟階段的關鍵時期,為此本研究選擇高二學生為研究群體．被試是從曲阜師范大學附屬中學高二年級隨機抽取的2個普通理科教學班的94名學生,被試作答時間為35min．被試信息見表2．

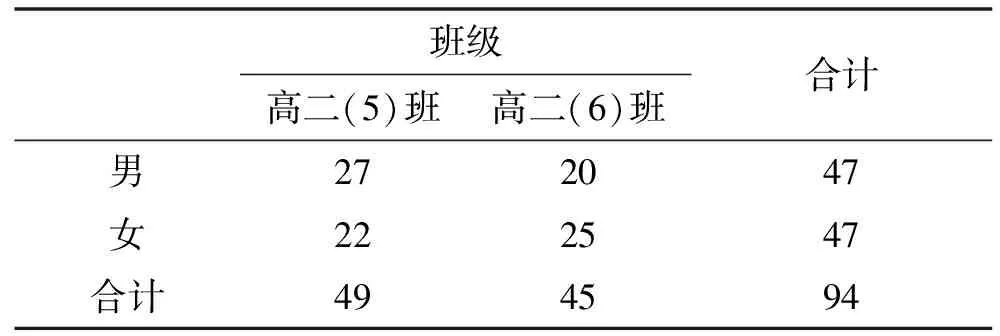
表2 有效被試分布信息

3 研究結果

3.1 測試卷的測量學指標

3.1.1 測試卷的難度

用全體被試得分率來表征題目的難度系數,數值越小表明難度越大．基于測量數據計算了所有試題的難度系數,結果見表3．

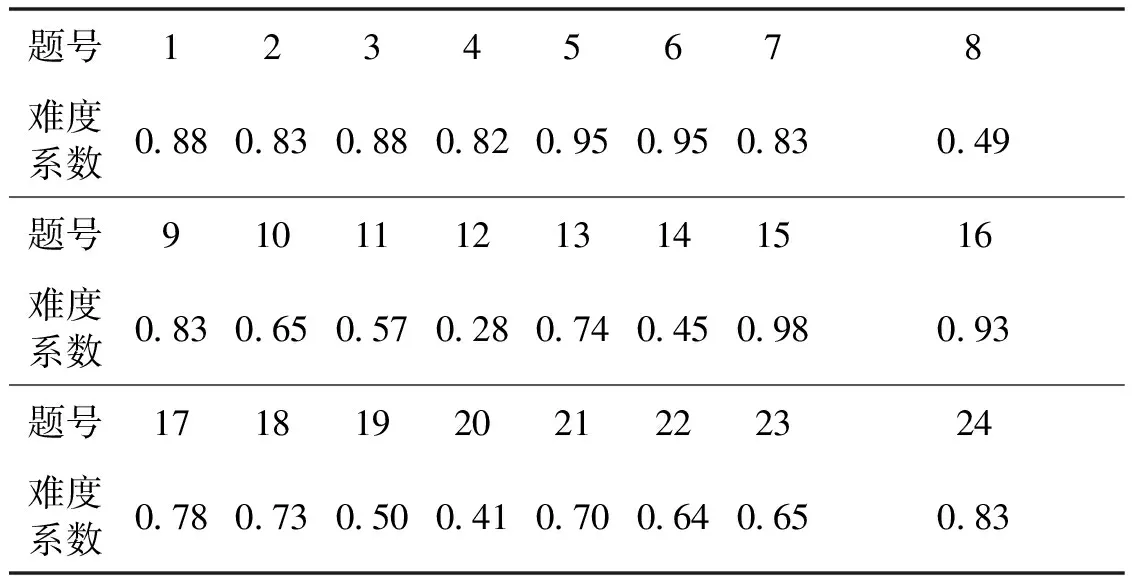
表3 24道試題的難度系數

由表3,試題難度系數大小介于0.28到0.98之間．難度最低的是第5、6題和第15、16題,難度較大的是第12題,難度系數達到了0.28．以0.5和0.7為界,簡單、適中和較難試題的比例為14∶5∶5,表明該測試卷的難度分布較為合理．

3.1.2 測試卷的區分度

利用高低分組法計算了測試卷的區分度,結果見表4．

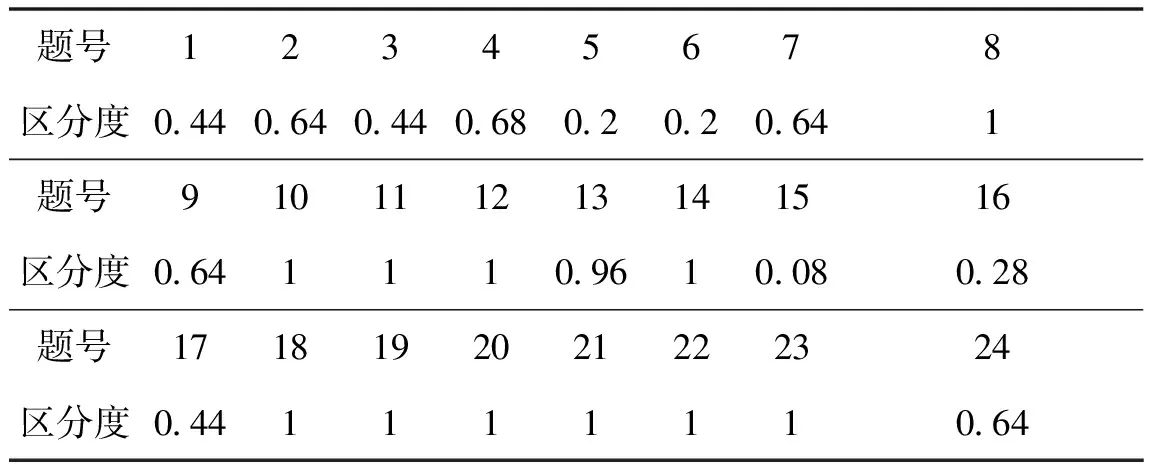
表4 24道測試題的區分度

由表4,除第5、6題和第15、16題的區分度過低外,其他題目的區分度均較為理想．上述4道題目區分度過低與題目的難度過小有關,高二學生已對這些題目有了相當成熟的認知,從測量學的角度看,這4道試題已不適宜區分高二學生的科學推理能力水平,但試卷整體仍具有較好的區分度．

3.2 科學推理能力得分的總體情況

3.2.1 總分分布情況

使用SPSS 18做出被試總分的分布情況,見圖1．

由圖1可知,學生科學推理能力的得分區間為4-24分,大部分被試的科學推理能力處于中等偏上的水平,位于17-18分數段的人數最多,其次是20-22和13-16分數段,位于低分區間和獲得滿分的人數均較少．在文獻[4]研究中,大學生的科學推理能力得分的峰值出現在20分左右(見圖2)．可見,與大學生相比,高二學生的科學推理能力仍有一定的發展空間．

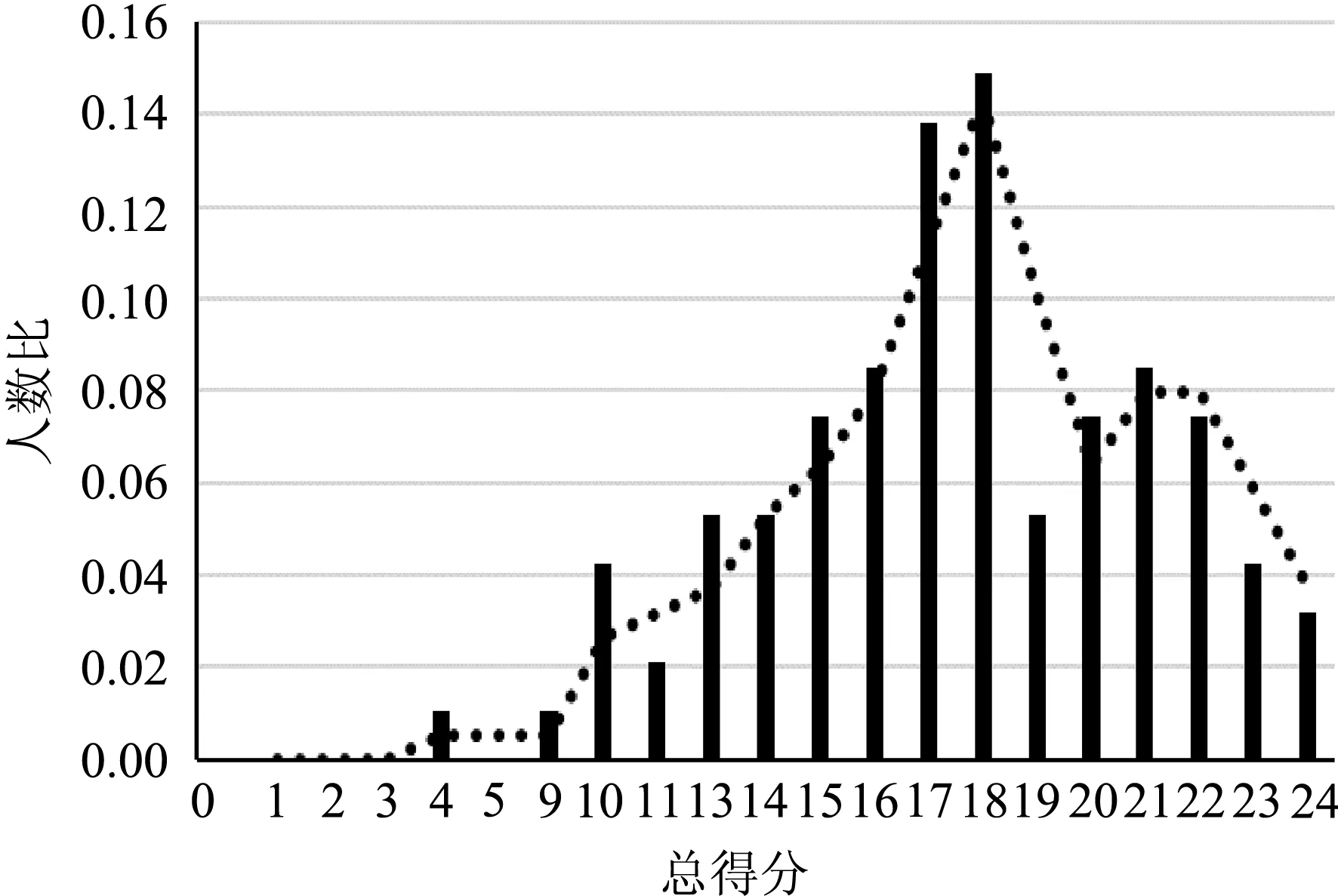
圖1 高二學生科學推理能力得分分布

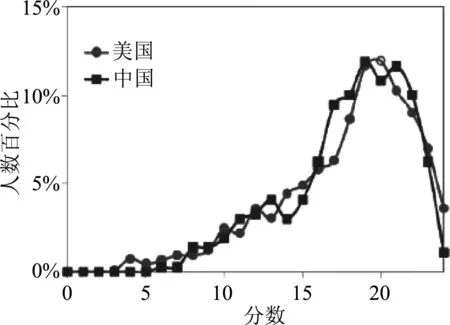
圖2 中美大學生科學推理能力得分分布

3.2.2 各維度得分情況

計算出被試在各能力維度的均值和標準差,結果見表5．

表5 各能力維度的均值和標準差

由于各維度題目數目不同,不易直接比較被試在各維度上的能力強弱．將上表中各維度的均值除以該維度的題目總數,并做出雷達圖,如圖3所示．

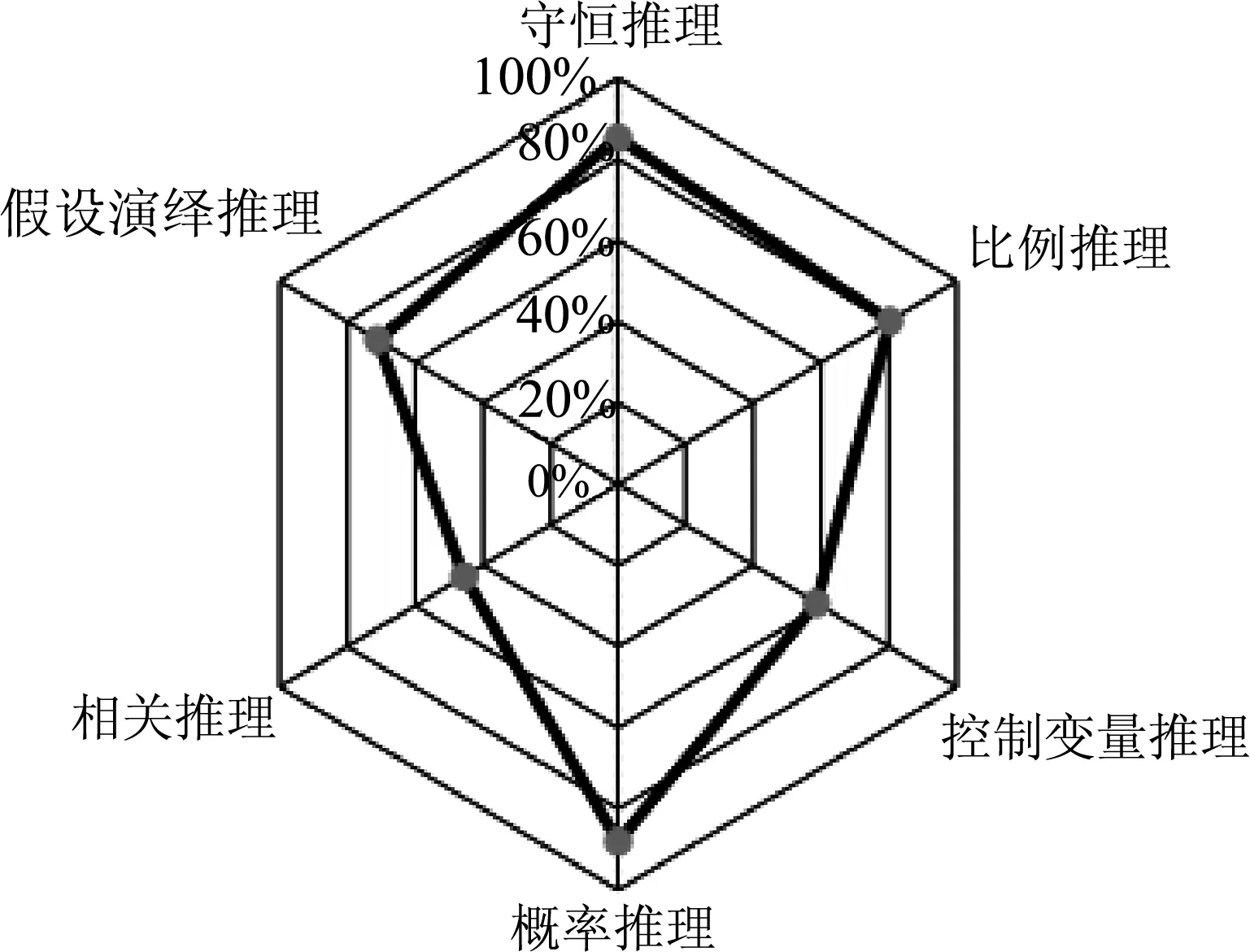
圖3 被試各科學推理能力維度雷達圖

由表5和圖3,被試的守恒推理、比例推理和概率推理水平較高,其次是假設演繹推理,控制變量推理和相關推理的水平則較低．同時,水平較低的兩個維度的標準差較大,表明被試個體在這兩個維度上的能力水平存在較大的差異．這一結果與張軼炳[5]研究中的大學生得分情況(見圖4)相比,本研究中被試的相關推理能力明顯偏弱．

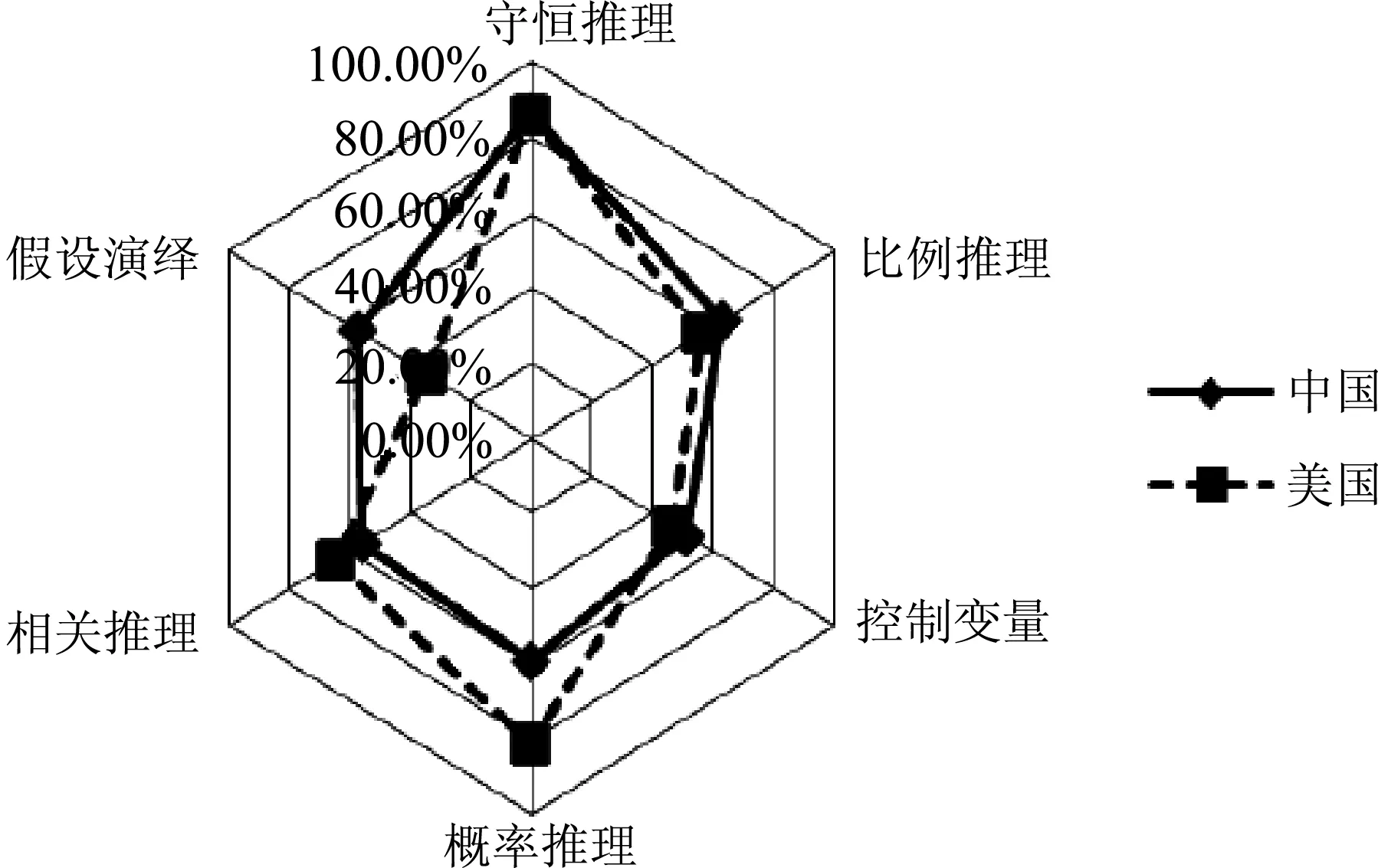
圖4 中美大學生各科學推理能力維度雷達圖

3.3 學生科學推理能力與性別的關系

被試在科學推理能力總分和6個維度得分的性別差異,結果見表6．

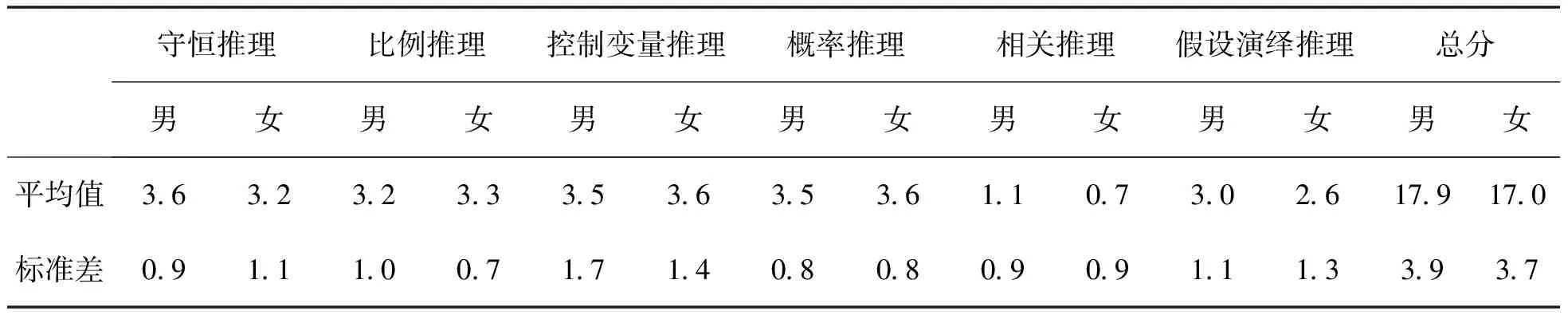
表6 科學推理能力總分及各維度得分的性別差異

不同性別的被試只在相關推理維度上存在顯著差異(t=2.044*,P<0.05),但在總分及其他能力維度上均不存在顯著差異．總的說來,男女學生的科學推理能力水平相當,不存在顯著的性別差異．

3.4 科學推理能力與物理學習成績的關系

為了研究科學推理能力是否會影響物理學習成績,本研究采集了被試高二上學期的期末物理成績,與科學推理能力測試成績做了相關性分析,結果見表7．

表7 科學推理能力及其各維度得分與物理成績的相關性

相關分析結果表明,物理學習成績與科學推理能力成績呈正相關,相關系數為0.313,在0.01水平上顯著相關．具體到科學推理的各個維度,假設演繹推理與物理學習成績的相關最高,二者的相關系數為0.440,在0.01水平上顯著相關．其次是相關推理,與物理學習成績的相關系數為0.217,在0.05水平上表現出顯著的相關性,其他維度對物理學習成績的影響不大．

4 討論

4.1 高二學生的科學推理能力

一般認為,科學推理能力是個體的一般能力,不依賴于某一專門領域．比對包雷、[4]張軼炳[5]等對大學生科學推理能力水平的研究,高二學生的科學推理能力尚處于一個不完全成熟的階段．處于該階段學生的科學推理能力已經達到中等偏上的水平,其守恒推理、概率推理和比例推理已近乎完善,但假設演繹推理能力、控制變量推理和相關推理能力則需要進一步發展．如何發展學生的科學推理能力是需要進一步研究的課題．Benford等人[9]發現,個體科學推理能力的強弱、是否增長,與教學方式相關,采用探究式教學可以顯著提高學生的科學探究能力．為此,在物理教學中應積極開展探究式教學,并重視培養學生在假設演繹推理方面的能力．

4.2 科學推理能力的性別差異

馮秀梅等[6]在探討中美大學生科學推理能力的性別差異中發現,中美大學生的總體表現都存在性別差異,而中國學生的性別差異相對較小．李力舟等[10]對甘南藏族地區中學生科學推理能力的抽樣調查中也認為男生、女生之間科學推理能力水平存在著一定的差異,女生在高一階段科學能力的發展情況略優于男生．不同的是,本研究并未發現高二學生在科學推理能力上存在顯著的性別差異,與孫慧娟等[11]對寧夏地區理科生的科學推理能力測量結果相似．研究結果的不同可能與樣本的選取有關,男女生的科學推理能力是否存在差異,仍需進一步探討．

4.3 物理學習成績與科學推理能力

不少研究都考查了科學推理能力與學習成績的關系．包雷[4]運用對比的方法,發現中美兩國學生雖然在物理學習成績方面存在較大差異,但是兩國學生科學推理能力卻近乎相同,即物理成績的優劣對學生科學推理能力的影響不大．但包雷研究的是兩種不同教育環境下學生的情況,成績的差異可能更多地受到教育環境的影響．與此不同的是,本研究選擇同一教學環境下的兩個平行班級,盡可能排除了無關因素的影響．梁美怡[12]計算了初中生物理學習成績與科學推理能力的相關,結果表明兩者的相關系數在0.25-0.3之間,與本研究結果相似．本研究還發現,科學推理能力對高中生物理學習成績的影響主要體現在假設演繹推理和相關推理兩個能力維度上,其中假設演繹推理維度的影響最為顯著．梁美怡[12]對初中生的研究表明,控制變量和假設演繹推理對物理學習成績影響較大．可見,不論是初中生還是高中生,假設演繹推理能力對物理考試的成敗具有顯著影響．我國的物理試題一般都是給出問題情境,由學生分析作答,在這一過程中,恰好需要用到假設演繹推理．這就提示我們,提高中學生的物理學習成績的重要途徑便是培養學生的假設演繹推理能力．

5 研究結論

本研究主要得到以下結論: (1) LCTSR 2000測試卷具有較為理想的難度和區分度．(2) 大部分高二學生的科學推理能力處于中等偏上的水平,與大學生相比,仍有一定的發展空間．(3) 高二學生在概率推理、守恒推理和比例推理上能力水平較高,其次是假設演繹推理能力,控制變量推理和相關推理能力水平則較低．(4) 高二學生的科學推理能力不存在顯著的性別差異．(5) 科學推理能力與物理學習成績的相關為0.313,其中,假設演繹推理對成績的影響最為顯著．