磁浮平面電機Halbach磁鋼陣列中梯形磁鋼的應用*

劉廣斗，張紅梅，明五一

（1.中國石油大學（華東）機電工程學院，山東青島 266580；2.廣東華中科技大學工業技術研究院廣東省制造裝備數字化重點實驗室，廣東東莞 523808）

0 引言

在許多工業設備中，例如拾取和放置裝置、光刻機以及檢測系統等，都在平面上定位和運動。磁浮平面電機因為結構簡單，高速以其高精度受到越來越多的關注[1-4]。在磁浮平面電機中使用的是Halbach磁鋼陣列[5-6]，如圖1所示。此陣列由于磁鋼排布的關系具有單邊性，能夠使一側的磁場增強，且強磁場具有良好的正弦分布，可以降低電磁力的波動。同時，磁浮平面電機中無鐵芯和背鐵，降低電機總體質量，這在高加速裝置中是很好的優點。

圖1 磁浮平面電機結構示意圖Fig.1 The structure diagram of magnetically levitated planar motor

Halbach陣列是由Klaus Halbach首先提出，現在已經廣泛應用在直線、管狀、平面等各種磁浮電機中。經過長時間的應用和發展，不僅僅是矩形磁鋼，還有一些三角形、梯形等磁鋼也開始在Halbach陣列中使用。文獻[7]的雙邊非Halbach陣列直線電機中，使用梯形磁鋼替換矩形磁鋼，并應用疊加原理得到近似磁場。文獻[8]的雙邊直線電機中，用梯形磁鋼組成Halbach陣列，磁場由所有單個磁鋼的磁場疊加而得到。文獻[9]在管狀電機中使用梯形陣列，用疊加原理得到并分析磁感應強度，但管狀電機陣列與平面電機Halbach陣列的邊界條件不同。本文作者推導梯形磁鋼組成陣列的磁感應強度解析表達式，通過分析Halbach陣列磁感應強度峰值和高階諧波誤差得到最優的y向磁化磁鋼邊長與極距比值，并分析梯形磁鋼對陣列空隙磁感應強度的影響。

1 梯形磁鋼陣列建模

1.1 梯形磁鋼陣列

在磁浮平面電機中，用梯形磁鋼替換矩形磁鋼得到梯形磁鋼陣列[10]，如圖2所示。梯形磁鋼也可以通過改變轉角θ由矩形磁鋼得到。其中，箭頭表示磁場方向是由S極指向N極。τ是磁鋼陣列的極距，τm是y向磁化磁鋼底邊的長度，h是磁鋼陣列的高度。

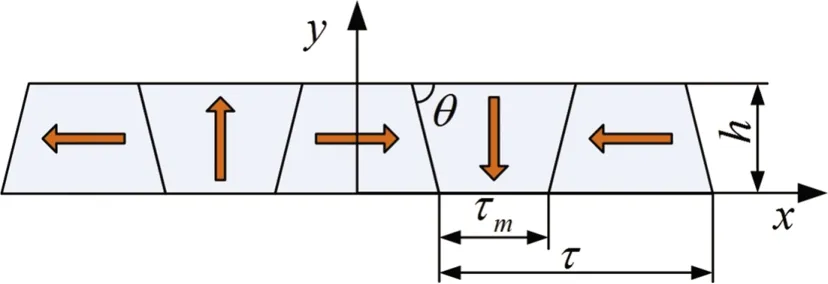
圖2 梯形磁鋼陣列Fig.2 The trapezoidal magnets array

計算梯形磁鋼陣列磁感應強度用到如下假設：

（1）磁鋼陣列在x方向無限延伸，因此磁鋼陣列的端部效應可以忽略；

（2）磁鋼均勻磁化。

根據上述假設，把磁鋼陣列劃分n等份，如圖3所示。應用疊加原理，整個梯形磁鋼陣列的磁感應強度可由n層矩形磁鋼陣列的磁感應強度相加得到。選取其中一層，即第i層進行分析，計算第i層磁鋼陣列的結構參數。

圖3 梯形磁鋼陣列n層劃分Fig.3 The n layers division of trapezoidal magnets array

由圖3可知每層磁鋼陣列的極距都相同。圖4是梯形磁鋼陣列的第i層y向磁化梯形磁鋼，根據梯形磁鋼的尺寸參數，第i層磁鋼陣列的參數如下

式中：hi和hi+1分別是第i層磁鋼陣列的底邊和頂邊高度，τmi是第i層y向磁化磁鋼底邊的長度。

圖4 磁鋼陣列的第i層y向磁化梯形磁鋼Fig.4 The y-direction magnetized trapezoidal magnet in the i layer of magnets array

1.2 第i層磁鋼陣列的磁感應強度

磁鋼陣列中只有x和y方向磁化的磁鋼，所以磁鋼陣列為二維磁場分布[11]。第i層磁鋼陣列的磁化強度可以表示為：

圖5為第i層Halbach磁鋼陣列的x和y向磁化強度分布。由前面假設不考慮磁鋼陣列的端部效應，使用傅里葉級數得到第i層Halbach磁鋼陣列的磁化強度表達式

式中：k是諧波數，Br是磁鋼剩余磁化強度，μ0是真空磁導率。

圖5 第i層Halbach磁鋼陣列Fig.5 The i layer of the Halbach magnets array

計算第i層Halbach磁鋼陣列的磁感應強度，可以劃分3個區域，如圖6所示。區域1和3為空氣，區域2為磁鋼陣列。因為沒有外加電流，所以引入磁標勢計算磁鋼陣列磁感應強度。由麥克斯韋方程組，各個區域的控制方程如下：

式中：Ψ1，3是區域1和3的磁標勢，Ψ2是區域2的磁標勢，μr是磁鋼相對磁導率。

圖6 磁感應強度區域劃分Fig.6 The division of magnetic flux density

根據磁場中不同磁介質分界面上的邊值關系，得到如下邊界條件：

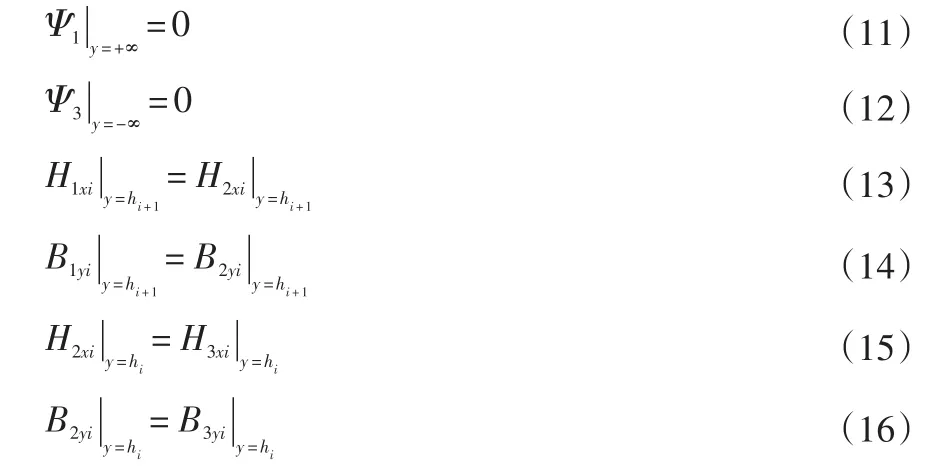
式中：H1xi、H2xi、H3xi分別是區域1、2、3磁場強度的x向分量，B1xi、B2xi、B3xi分別是區域1、2、3磁感應強度的y向分量。

使用分離變量法并結合邊界條件求解控制方程（9）和（10）。設定要使用的磁場區域為區域3。在區域3中，磁感應強度與磁標勢的關系式如下：

得到區域3磁感應強度的表達式：

1.3 梯形磁鋼陣列磁感應強度

根據圖6磁感應強度區域的劃分可知，每一層Hal?bach磁鋼陣列的磁感應強度區域分布情況相同，不同之處在于磁鋼陣列底邊和頂邊坐標的變化。所以，由疊加原理得到梯形磁鋼陣列的磁感應強度為：

其中，當n趨于無窮大時，得到磁感應強度精確的解析表達式。從工程角度分析，解析模型只需要滿足一定精度即可，所以通過對比解析模型和有限元模型來確定n的取值。

設定梯形磁鋼陣列的參數為Br=1.2，n=5，τ=20 mm，h=10 mm，τm=5 mm。把解析模型得到的磁感應強度與有限元模型得到的磁感應強度對比，結果如圖7所示。觀察圖形可知，解析模型和有限元模型具有很好的一致性。Bx和By的最大誤差分別為0.007 T和0.006 T，占各自峰值的1.77%和1.27%，精度足可以滿足工程計算。

圖7 解析模型和有限元模型磁感應強度對比Fig.7 The division of magnetic flux density

2 Halbach陣列參數分析

以Halbach矩形磁鋼陣列為例，參數選擇一般遵循磁感應強度最大或者高階諧波最小的原則。通常陣列的極距和高度都為初始設計值，那么y向磁化磁鋼的邊長τm成為影響磁鋼陣列磁感應強度大小的主要結構參數。在磁浮平面電機中，Halbach矩形磁鋼陣列的Bx和By分別產生懸浮力和驅動力，其中驅動力大小是平面電機的一個關鍵指標。因此，對By進行分析選擇合適的磁鋼陣列結構參數，Halbach矩形磁鋼陣列的高度和極距和1.3節的相同。

2.1 諧波磁感應強度

以y向磁化磁鋼的邊長τm與極距τ的比值為參數，得到By在距離磁鋼陣列底邊3 mm空隙處各個諧波的峰值，如圖8所示。各個諧波的峰值以τm/τ=0.5為中心對稱分布，其中3階諧波有最大的高階諧波幅值，當τm/τ=0.5，此時基波的峰值最大。

2.2 高階諧波誤差

為了更直觀的表示高階諧波與τm/τ的關系，引入均方根（RMS）表示高階諧波的誤差。均方根的表達式為：

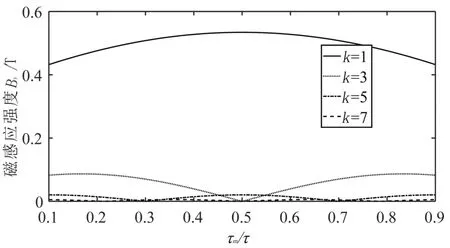
圖8 By各個諧波的峰值Fig.8 The peak value of each harmonic in y-component of magnetic flux density

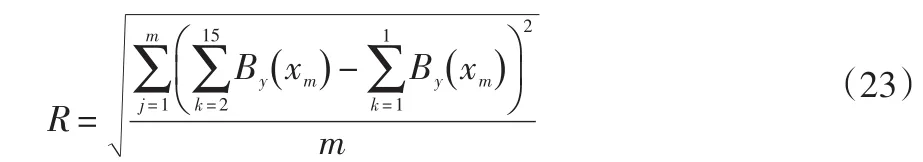
式中：m是x軸所選區域劃分的點數。

根據磁感應強度的周期性，選取分析范圍x=[0，τ]，劃分100等份，距離磁鋼陣列底邊3 mm。得到高階諧波的均方根隨著比值τm/τ變化的波形，如圖9所示。觀察波形可知，高階諧波的均方根以τm/τ=0.5為中心對稱分布。當τm/τ=0.5，得到高階諧波的均方根最小值，即高階諧波誤差最小。

圖9 高階諧波的均方根（RMS）Fig.9 The root mean square of higher harmonics

從上述兩個方面分析，τm/τ=0.5既能得到最大的基波峰值，又能得到最小的高階諧波誤差。所以，Halbach矩形磁鋼陣列的最優結構參數為τm/τ=0.5。

3 梯形磁鋼對磁感應強度的影響

分析改變磁鋼形狀對空隙磁感應強度的影響，Hal?bach磁鋼陣列結構參數和1.3節的相同。以轉角θ為參數，變化范圍與高度和極距有關，在此結構參數下為從45°到135°。得到距離磁鋼陣列底邊3 mm空隙處By峰值和高階諧波誤差隨著轉角θ變化的波形，如圖10所示。觀察圖形，可知在50°之后，磁感應強度的峰值隨著轉角的增大而減小。高階諧波的誤差則是以90°為中心對稱分布，而且在90°處高階諧波誤差最小。隨著轉角的變化，磁鋼陣列的磁感應強度峰值變化范圍是從0.428 T到0.574 T，變化率達到34.11%。所以，用梯形磁鋼可以大范圍改變磁鋼陣列的磁感應強度，但同時也引起高階諧波誤差的增大。

圖10 磁感應強度峰值和高階諧波誤差隨轉角θ變化的波形Fig.10 The waveform of peak value of magnetic flux density and root mean square of higher harmonics varying with the theta

4 結論

（1）應用梯形磁鋼到磁浮平面電機Halbach磁鋼陣列，得到梯形磁鋼陣列。利用疊加原理，通過磁標勢和邊界條件得到整個梯形磁鋼陣列的磁感應強度解析表達式。并通過有限元模型驗證。

（2）分別從磁感應強度最大和高階諧波最小兩方面分析Halbach矩形磁鋼陣列，得到最優的結構參數。

（3）分析隨轉角變化的磁感應強度峰值和高階諧波誤差，梯形磁鋼可以大范圍改變磁鋼陣列的磁感應強度。