基于自適應粒子群算法的玻璃澄清環境評價模型分析*

姜夢一

（廣東工業大學機電工程學院，廣東廣州 510006）

0 引言

玻璃制品的需求量逐年增加，玻璃窯爐是玻璃加工企業的心臟，其主要生產工序包括熱源供應、玻璃液熔制、余熱回收、排煙4個部分[1]。其中玻璃液熔制過程中澄清環境與玻璃產品質量息息相關。澄清過程是從熔融的玻璃液中排除氣泡缺陷，其中涉及到復雜的物理、化學和傳質傳熱過程，難以對澄清環境進行評估，進而對產品質量的穩定性帶來一定的波動。

目前對澄清過程的研究主要集中在對澄清過程中氣泡的行為及相關參數進行優化。Vander Schaaf J和Beerkens R G C[2]通過對氣泡行為研究得到氣泡形成的模型。Kim D S和Dutton B C，Hrma P[3]等總結了窯爐熔制氛圍為對氣泡的影響。Nemec L和Cincibusova[4]得出氣泡消除過程中對玻璃液熔制的影響。賀建雄[5]通過對熔體中氣泡行為特征建立數學模型，分析熔窯氣泡澄清困難的原因，并基于這個原因對該熔窯的工藝參數進行優化調整。馬晶[6]通過計算玻璃液流場分布，對不同工作制度下玻璃液中氣泡澄清過程進行模擬，得到玻璃液中氣泡澄清情況最好的溫度制度。趙國昌[7]提出澄清指數，采用數值模擬手段來定量化評價和分析玻璃熔制澄清過程，并考察熔窯結構和參數對玻璃熔制質量的影響。目前的研究中對氣泡行為與澄清時間關系的研究多為簡單的定性描述，缺少對澄清條件進行定量分析。

本文作者引入澄清因子作為評估澄清條件的指標，對澄清時間和氣泡逸出時間之間的關系進行定量化分析，建立澄清評估模型，并采用自適應變異粒子群算法對模型求解，得到優化的澄清參數，將優化后的生產參數應用于實際生產調試。

1 玻璃熔化過程評價模型

1.1 熔化過程玻璃液流特性分析

通過研究帶窯坎的馬蹄焰池窯內玻璃液的流動規律，如圖1所示，玻璃液在熔化部形成環流，環流流向配合料層的強勁回流有效阻擋了表面的浮渣，窯坎的設置迫使生產流向上翻轉，翻轉到接近玻璃液表面的液流經歷熱點區域的高溫澄清過程，并在窯坎后分層折返，并從澄清區域的底部經過流液洞進入工作部，從而能夠獲得高質量的玻璃液。

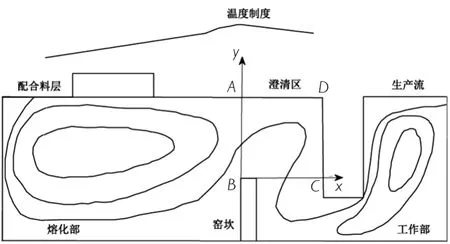
圖1 玻璃液流圖

1.2 熔制過程澄清條件評價模型的建立

1.2.1 澄清過程理論分析

熔制過程中由于各種夾雜物的存在而引起的玻璃體整體均勻性破壞，稱為玻璃體的缺陷。其中氣泡缺陷是在配合料熔化和玻璃液形成的過程中發出的大量氣體，體積大約占到玻璃熔體的幾千倍，直到玻璃完全成形后，仍有一部分未完全從玻璃液中完全逸出，故以氣泡的形式殘留在玻璃液中，不僅影響玻璃外觀質量，也會影響透明度和機械強度。

澄清過程就是消除液流中的氣泡。通過分析液流特征可知生產流在澄清區域的時間越長，而氣泡逸出玻璃液面的時間越短，澄清效果越好。

1.2.2 澄清過程評價模型

澄清因子是生產流在澄清時間內逸出氣泡程度，是判斷澄清條件好壞的重要指標。清華大學的趙國昌認為澄清因子的定義表示如下：

式中：tBC為生產流在區域ABCD所停留的時間；tAB為單個氣泡從A上升到B的時間。

澄清指數在考慮澄清時間長短的情況下，又考慮了氣泡逸出的難易程度，其中包含了流場信息和溫度場信息。澄清因子越大就表示在澄清時間內氣泡能夠逸出的時間越久，澄清效果就會越好。

（1）澄清過程氣泡逸出時間模型

針對氣泡上升過程的研究，Duineveld用實驗的方法測定氣泡的上升速度，結果表明氣泡上浮速度是一個從0逐漸在增加到末速度的過程[8]。

令氣泡的質量為mb:

氣泡受到的浮力Ff:

式中： ρl是液體的密度。

氣泡受到的重力Fg:

式中： ρb是氣泡的密度。

氣泡的曳力系數Cd反映了氣泡在上升過程中阻力的變化情況，有研究表明當氣泡在液相中上升的時候，曳力系數會隨著雷諾數Re的增大而減小。當氣泡在液相中的上升速度穩定的時候其曳力系數保持恒定。

式中： μ是液體動力粘滯系數，Kb是Basset力經驗系數，通常Basset力經驗系數，其中加速度模數

綜合上述對氣泡受力分析得到力平衡方程：

通過整理方程并代入上式可得到：

（2）生產流在澄清區域停留的時間模型

生產流在澄清區域停留的時間tBC：

式中：為vglass為玻璃液的流速 。

玻璃液的點速度v是衡量池窯內玻璃液流動程度的數據，可以用來計算玻璃液的流速[9]。

式中：vi是玻璃液流第i點的點速度；n是在各段內設置的點數。

玻璃液的流量系數F是玻璃液的流量與實際拉引量的比值。澄清段的流量系數F：

式中：A和B是經驗系數；v是該段玻璃液的平均點速度。

式中：vglass是玻璃液流的速度；F是流量系數；G是拉引量；r是玻璃液的平均密度，根據各段內溫度計算取得； lBC是玻璃液流的厚度；b是池窯寬度。

（3）澄清條件評價模型

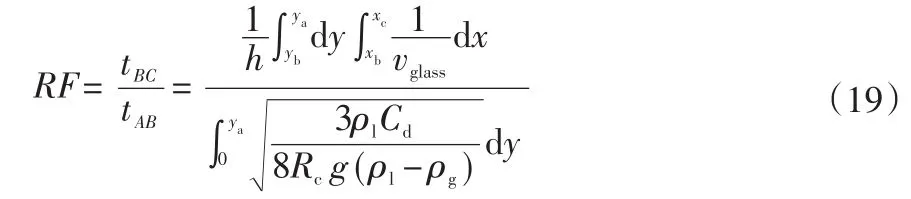
2 模型求解

2.1 粒子群算法原理

粒子群優化算法中每個優化問題的潛在解稱為粒子，粒子在搜索空間中以一定的速度飛行，這個速度可以根據自身和他人的經驗動態調整。在一個d 維的目標搜索空間中，有一個種群代表m個潛在問題解的粒子，其中…，m表示第i個粒子在d維解空間的一個矢量點，vi=[vi1,vi2,…,vim]，i=1，2，…，m表示第i個粒子的飛行速度，第i個粒子搜索到的最優位置為 pi=[pi1,pi2,…,pim]，整個群體搜索到的最優位置為 pg=[pi1,pi2,…,pim]。

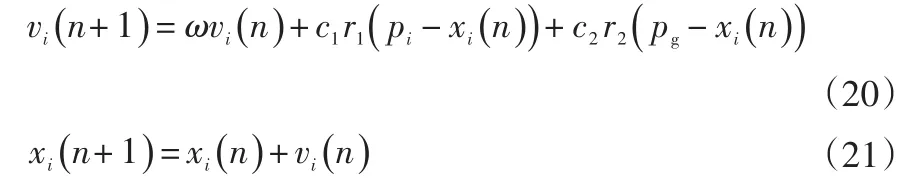
式中：c1,c2為大于0的加速系數，稱為學習因子，分別用于調節該粒子向自身已經尋找到的最優位置和其他同伴已經尋找到的最有未知方向飛行的最大步長；r1,r2是介于0到1之間的隨機數；n為迭代次數，就是粒子的飛行步數；vi的范圍在[-vmax,vmax]之間，vmax根據實際問題確定；ω是非負數，一般在0.1到0.9之間取值，稱為慣性因子。

2.2 自適應變異

2.2.1 群體適應度方差σ2

假設粒子群的例子數目為n，fi為第i個粒子的適應度，favg為平均適應度，σ2為群體適應度方差，則σ2可以定義為：

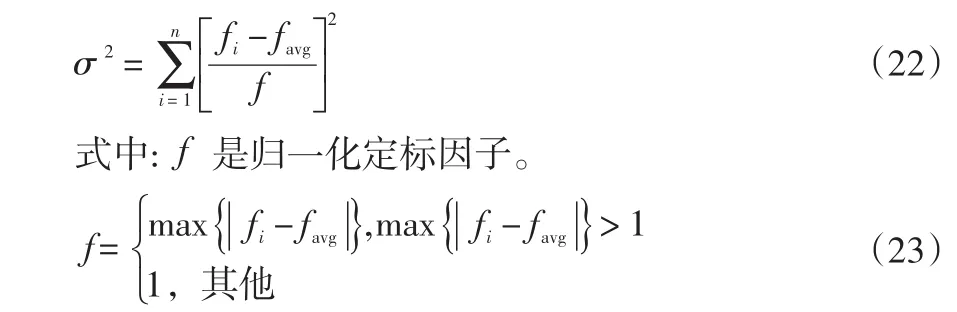
群體適應度方差體現了群體中所有粒子的收斂程度，值越小越趨于收斂，反之則處于隨機搜索階段。

2.2.2 粒子收斂

粒子的收斂是指粒子最終停留在搜索空間的一個位置p。假設粒子群中單個粒子在t時刻的位置是x（t），p是搜索空間的任意位置，則粒子收斂為：

2.2.3 自適應變異思想

若群體適應度方差為0，但此時的最優解不是理論最優值，此時算法就發生了早熟收斂。此時將變異操作設計成一個隨機算子，對滿足變異條件的當前最優位置按照概率 pm變異。

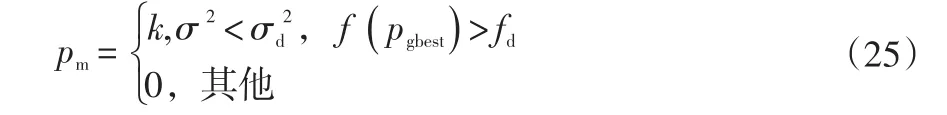
式中：k∈[0 . 1,0.3]，fd可設置為理論最優值。

對 pgbest的變異操作，采用增加隨機擾動的方法，為 p的第k維取值，η是服從Gauss(0,1)分布的隨gbest機變量，則

2.2.4 算法流程

針對PSO算法早熟收斂的適應度方差進化算法具體流程如下：

（1）隨機初始化粒子群中每個粒子的速度與位置。

（2） pi設置為當前位置，pg設置為初始群體中最佳位置。

（3）判斷算法是否收斂，如果收斂則轉向（8），否則執行（4）。

（4）針對每個粒子，將其自身的適應值與所經歷過的最優位置 pi=[pi1,pi2,…,pim]的適應值進行比較，如果更好，則將其作為當前的最優位置。

針對每個粒子，將其適應值與全局所經歷的最優位置pg=[pi1,pi2,…,pim]的適應值進行比較，如果更好，則將其作為當前的全局最優位置。

（5）計算適應度方差σ2，及f(pgbest)，及變異概率pm。

（6）隨機數r∈[0 , 1]，如果r＜pm，則按照（4）執行變異操作，否則轉向（7）。

（7）判斷算法是否收斂，如果收斂，執行（8），否則轉向（4）。

（8）輸出 pgbest，算法運行結束。

2.3 澄清過程最優化問題

2.3.1 澄清過程的數學描述

澄清過程的最優問題可以描述為一個約束非線性規劃問題，用下式所示：

式中： f(x)是需要優化的目標，gi(x)是約束條件，[aj,bj]是各個變量的取值范圍。

2.3.2 優化變量及約束條件

碹頂溫度（℃） 1 320≤tc≤1 600

排煙溫度（℃） 200≤tp≤380

拉引量（t/d） 100≤G≤200

2.4 優化結果及分析

利用上述算法對澄清因子進行優化分析，表1列出澄清因子評價模型參數，表2列出優化變量及澄清因子的優化結果，且各個性能參數都在合理的約束范圍之內。

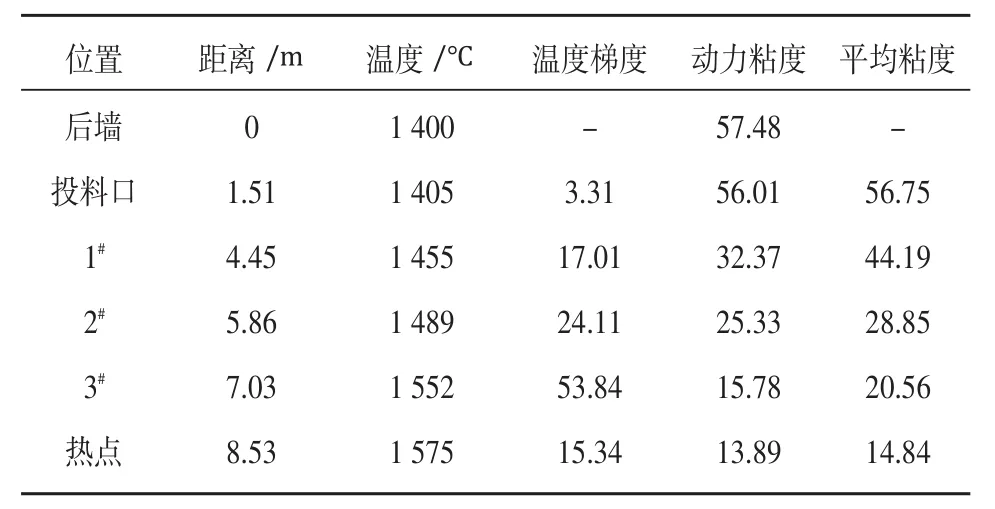
表1 澄清因子評價模型參數

表2 優化變量及目標函數

2.5 優化結果及分析

數學模擬達到令人滿意的結果，對馬蹄焰窯爐進行工業調試，在熔窯整體穩定運行的情況下進行考察，以最終玻璃成品中氣泡缺陷為考察指標。結果表明通過最終的工業參數調試，該熔窯的玻璃氣泡缺陷問題得到了解決，玻璃產品的質量也有了明顯的提高。如圖2所示，通過參數調試后的10 m2玻璃板的氣泡缺陷數目從原來的248個降低為5個，在熔窯各方面穩定運行的情況下，氣泡缺陷減少效果非常明顯。

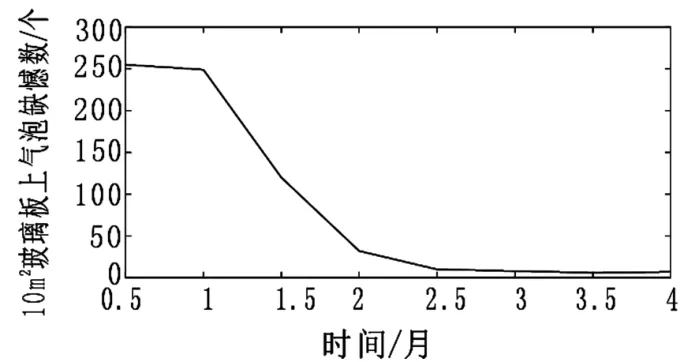
圖2 工業調試前后玻璃產品的氣泡缺陷統計

3 結論

在對玻璃液流規律的研究的基礎上引入澄清因子作為評估澄清條件的指標，建立澄清過程評價模型。通過對生產流在澄清區域的停留時間和氣泡在澄清區域的上升時間進行定量化分析，并運用自適應變異的粒子群算法對該模型進行求解，得到全局最優化結果，并將優化后的參數應用于實際的工業生產調試，得到非常滿意的結果。結果表明通過對澄清條件進行評價進而對參數進行優化在實際生產中具有非常重要的意義。