逆抽樣條件下配對試驗設計中優比的統計推斷
江紹萍,李慧敏,繆 清
(云南民族大學 數學與計算機科學學院,昆明 650500)
0 引言
在生物醫學研究中,人們常常想知道同一類藥物的兩種藥品藥效、同種疾病的兩種處理方法的成功率是否一樣?為回答上述問題,人們考慮配對試驗設計下的等價性檢驗。如對n個患某種疾病的病人使用標準處理方法進行治療,而對另外n個病人(與前一種治療方法的病人有相同的病情、年齡、性別等)使用一種新的處理方法進行治療,或對n個病人同時使用兩種不同的診斷方法進行診斷,以評價兩種診斷方法的檢驗敏感度或特異度的等價性等,這就得到一個 2 × 2 的列聯表[1,2]。McNemar[3]最早采用2×2的列聯表進行兩種治療方法的等價性評價問題的研究。相繼的很多學者[4-7]采用風險差、風險比、優比等進行治療方法的非劣性和等價性檢驗問題的研究。
上述研究是建立在抽樣總數固定的基礎上進行的,然而,實際臨床實驗中,經常遇到小概率問題,如一些罕見的疾病。此時若抽樣總數固定,則抽樣中可能會出現列聯表的某些格子里樣本數很少甚至為零的情況,從而使得樣本落入相應格子的概率的極大似然估計為零(而實際中并非為零)[2];或者人們感興趣的是其中一個格子抽到r個病例的情況,而此時的抽樣總數可能不是獲得感興趣r個病例時所需的最小抽樣總數,這不僅有悖于道德倫理,也造成資源浪費。為避免上述情況,在2×2的列聯表研究中,采用逆抽樣(也成為負二項抽樣)進行數據處理,既符合實際理論的需要,又兼顧道德倫理的合理性[2]。所謂逆抽樣,就是事先確定感興趣的樣本數,然后持續地進行抽樣,直到感興趣的樣本數達到預先規定的數目。近年來,眾多學者[8-10]對逆抽樣條件下基于兩獨立樣本試驗設計的2×2的列聯表數據進行了多方面研究,而對逆抽樣條件下配對試驗設計2×2列聯表的研究成果較少。因而本文把逆抽樣方法加入到配對試驗設計2×2列聯表,通過優比進行統計推斷問題的研究。
1 概率密度函數及優比的定義
假定治療某種疾病有兩種治療方案(稱為標準治療方法和新方法),每種治療方案都是一個二分量變量(即治療成功和治療失敗,分別記為1和0)。在抽樣過程中連續抽樣直到獲得x01(≥1)個標準治療方案成功而新治療方法失敗的樣本時才停止抽樣,由此得到配對的2×2列聯表如表1所示:
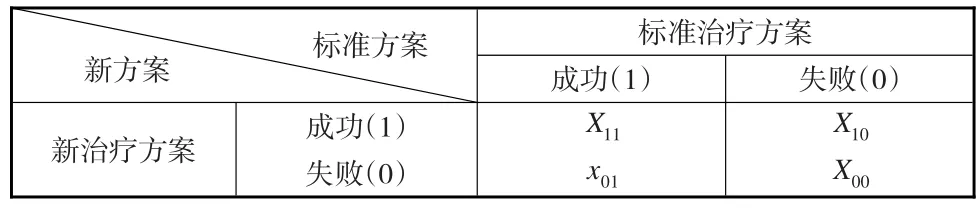
表1 某疾病新舊治療方案檢驗結果
其中x01是先前固定的正整數,隨機變量X11,X10和X00表示配對試驗設計中當獲得x01個先前固定的樣本時落入其他相應格子中的樣本數。記π11,π10,π01和π00分別表示配對試驗設計中樣本落入相應格子的概率。隨機變量X11,X10和X00的聯合概率密度函數為:
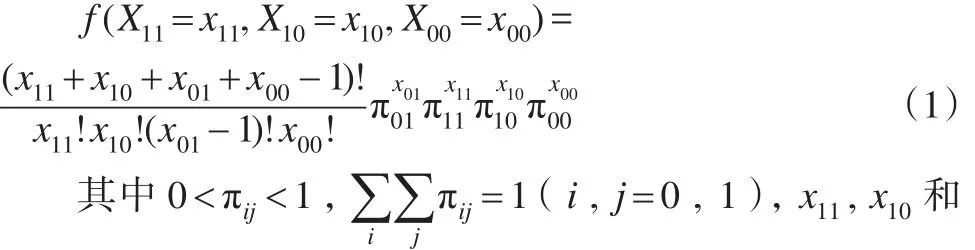
x00的取值分別為 0?,?1?,?2?。
根據Lachin[11]定義優比(Odds Ratio)為
因此,本文的假設檢驗為:

其中δ0為一個已知常數。根據優比的定義,得到π10=δπ01。因而觀測頻數 (x11,x10,x00)的對數似然函數為:
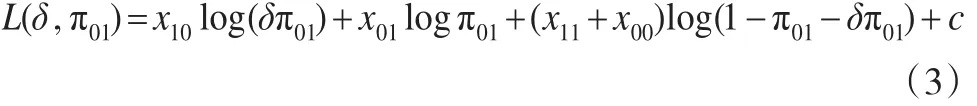
其中c為不依賴于參數δ和π01的常數,δ為感興趣參數,π01為討厭參數。
2 參數估計及統計量的建立
2.1 參數估計
記θ=(δ,π01),對數似然函數關于參數的一階導數和二階導數分別為:
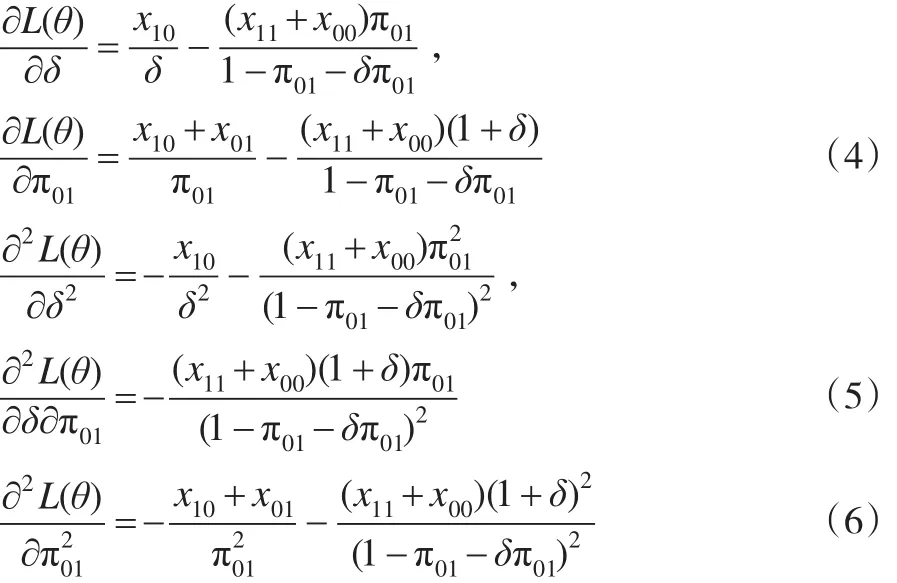
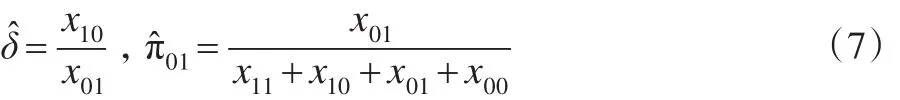
同理,可以求解在H0:δ=δ0條件下討厭參數的限定性極大似然估計。此時令,得到限定性條件下參數極大似然估計記,其中:
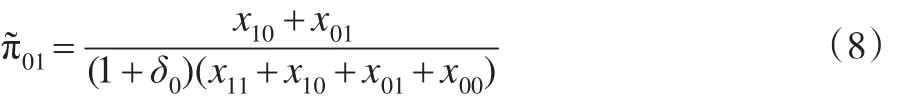
2.2 檢驗統計量的建立
以往通常采用delta方法求解感興趣參數的期望和方差,但delta方法是一種近似求解的方法,得到的結果帶有一定的偏差;為了避免出現這種偏差,文中采用Fisher-score的方法求解參數的方差。由此建立Fisher信息陣如下:
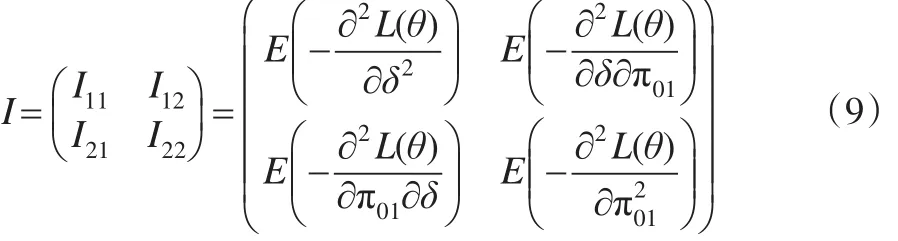
計算上述Fisher信息陣時,應注意到隨機變量x1j(j=1?,?0)服從參數為x01和的負二項分布,x00服從參數為x01和的負二項分布。通過求解Fisher信息陣的逆矩陣得到感興趣參數的方差為:
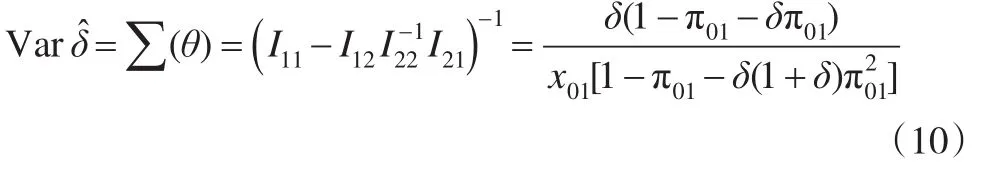
從而得到:
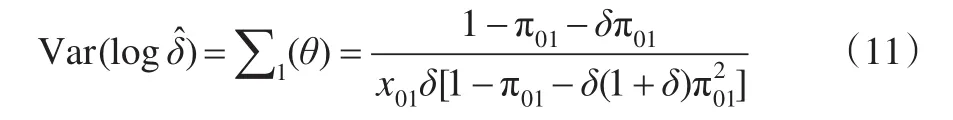
故建立六個檢驗統計量如下:
(1)Wald檢驗統計量(基于樣本方差):

(2)Wald檢驗統計量(基于原假設下方差):

(3)對數Wald檢驗統計量(基于樣本方差):
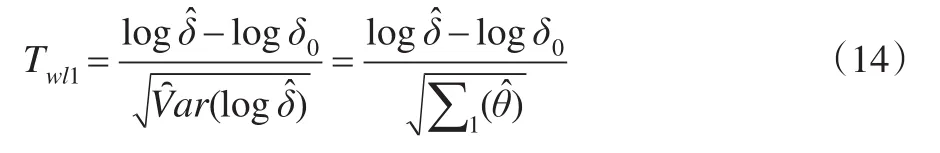
(4)對數Wald檢驗統計量(基于原假設下方差):
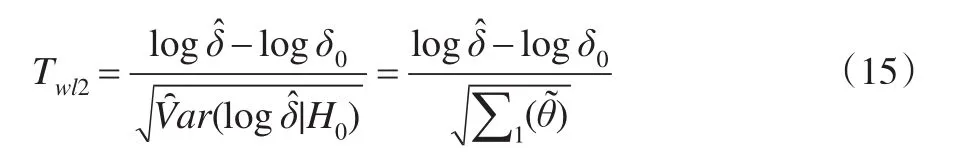
(5)Score檢驗統計量:
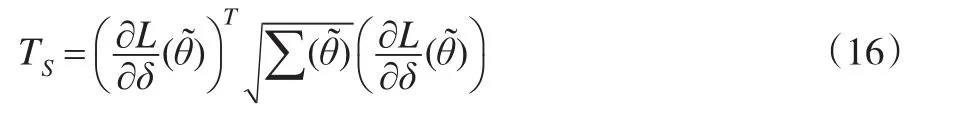
(6)似然比檢驗統計量:
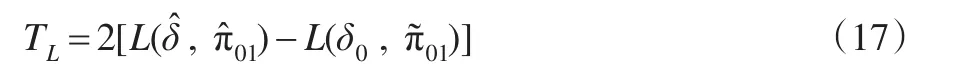
上述Wald型檢驗統計量、對數Wald型檢驗統計量漸進服從標準正態分布,而Score檢驗統計量和似然比檢驗統計量漸進服從自由度為1的卡方分布。
3 模擬研究
通過模擬研究比較上文提出的檢驗統計量的有效性,即通過在相同的樣本量和在各種參數設置下,產生10000個隨機數,并且計算這些檢驗統計量的經驗第一類錯誤率和經驗功效。如果經驗第一類錯誤率和事先給定的顯著性水平比較接近,則認為該檢驗統計量比較有效。在計算犯第一類錯誤的概率時,優比的取值為1.0,2.0,討厭參數π01的取值為0.05,0.1,0.15和0.2,樣本量的取值為10,20,30,50,80和100。在計算功效時,δ0=0.8 ,討厭參數 π01的取值為0.05,0.1,0.15和0.2,樣本量的取值為10,20,30,50,80和100。計算的結果如下頁表2和表3所示:
為了衡量模擬檢驗的效果,根據Tang等[12]中討論,如果經驗第一類錯誤率與名義第一錯誤率的比值超過1.1(即顯著性水平α=0.05而經驗第一類錯誤率大于0.055)時,稱為“寬松檢驗”;如果經驗第一類錯誤率與名義第一錯誤率的比值小于0.9(即顯著性水平α=0.05而經驗第一類錯誤率小于0.045)時,稱為“保守檢驗”;否則稱為“穩健檢驗”。所以根據表2和表3得到如下結論:(1)Wald統計量(基于原假設下方差)和Score統計量是穩健的;(2)Wald統計量(基于樣本方差)和對數Wald統計量(基于原假設下方差)是寬松的;(3)隨著樣本量x01和π01的增加,經驗第一類錯誤率越接近于顯著性水平;(4)參數δ0和π01的值固定后,各統計量得到的功效隨著樣本量x01的增加而增大。(5)參數δ0=0.25時,Score統計量計算得到的功效是最大并且犯第一類錯誤的概率更接近于顯著性水平。綜上所述,Score統計量具有較好的性質,在以后的研究問題中是可以采納的檢驗統計量。

表2假設檢驗H0:δ=δ0和顯著水平α=0.05下由10000個樣本計算得到的犯第一類錯誤的概率
4 結束語
現實生活中經常遇見逆抽樣問題和列聯表數據問題,以往都是單獨考慮這兩個問題,本文把兩者結合在一起進行優比的統計推斷研究,這為列聯表數據的研究提供了一種有效方法。通過模擬研究討論了文中引進的六個統計量所使用的條件,為以后的研究提供了參考。另外,生物醫學研究中的等價性評價問題除了轉化為相應統計指標(如優比、風險差、風險比等)進行假設檢驗外,還可以在后續研究中對逆抽樣條件下配對試驗設計的列聯表中相應統計指標進行區間估計問題研究。
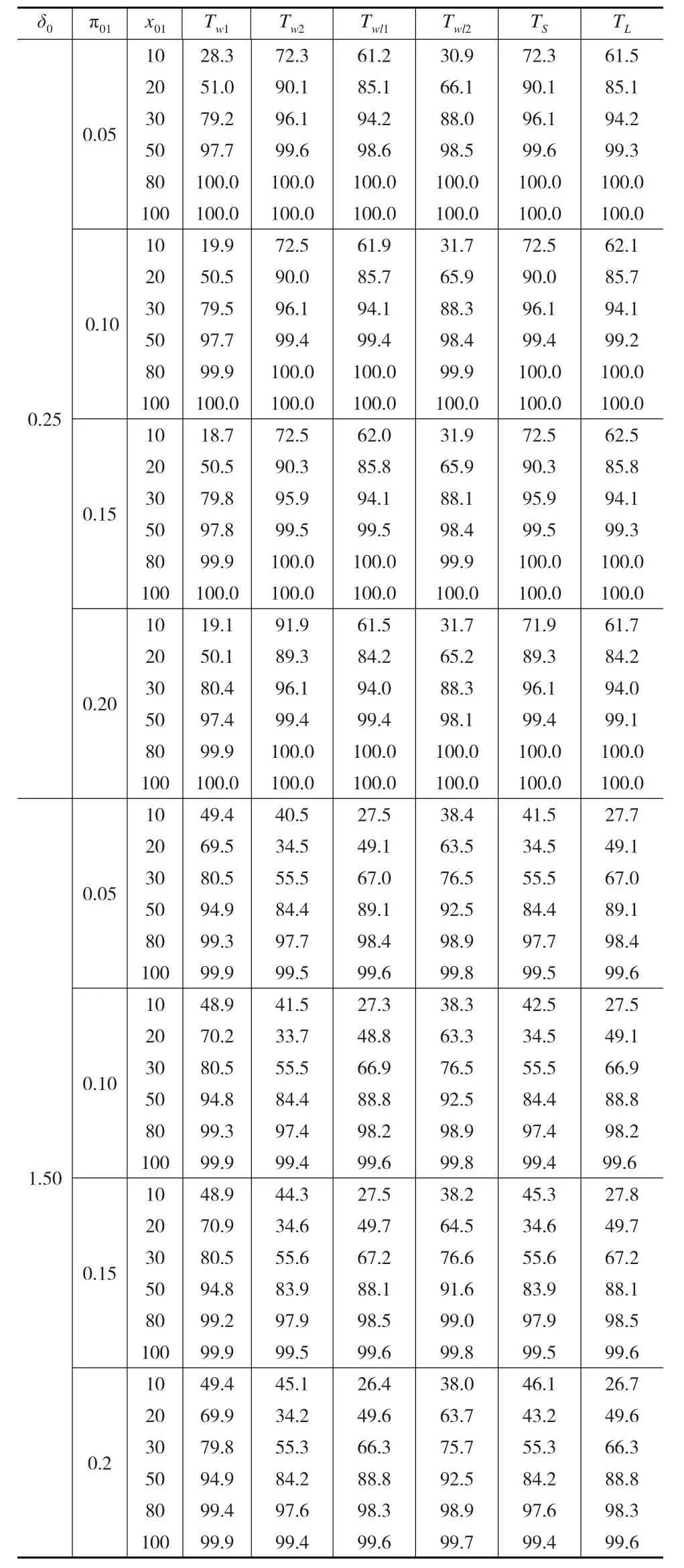
表3 假設檢驗H0:δ=δ0和顯著水平α=5%下由10000個樣本計算得到的經驗功效,其中δ1=0.8

