基于統計和混沌優化BP神經網絡融合模型的大壩變形預測分析

陳 嬋，田 曄

（江西省安義縣水務局，江西 安義330500）

0 引言

大壩原型監測數據的動態變化直接反映其運行性態，基于大壩原型監測數據，構建合理的大壩監測效應量模型并對大壩的監測效應量進行實時預測是大壩安全監控的重要內容，且監測效應量的準確預報對保障大壩的安全運行有著十分重要意義。工程實踐表明，大壩監測效應量受到庫水壓力、溫度、壩基、滲流、施工過程、時效等因素的影響，使得壩體、壩基以及近壩庫岸構成了一個復雜開放的非線性動力系統[1]。使大壩監測效應量具有混沌動力學特性，其監測的數據序列為混沌時間序列。由于大壩變形監測量直觀可靠、精度較高，可通過研究大壩變形的數據序列來反映大壩在環境與荷載互饋作用下變形性態的動態演變。

大壩變形監測的混沌時間序列數據有其特定非線性規律，解析方法一般很難表達這種特性，使得傳統統計模型的擬合精度高但預測效果不佳。BP神經網絡作為人工神經網絡中最重要的網絡之一，其特點是具有很強的自適應性和學習模仿能力，在工程中應用極為廣泛。大量實踐證明，基于誤差反傳遞算法的BP神經網絡有很強的映射能力，可有效剖析混沌時間序列的非線性特性。但傳統的BP神經網絡并未考慮到大壩的混沌動力學特性。因此，本文主要開展以下兩方面的研究：①基于統計模型分離出變形監測數據序列中除了可確定成分與隨機性成分外，對殘差項數據序列進行混沌特性判別；②對于帶有混沌特性殘差數據序列建立混沌優化BP神經網絡模型，從而對大壩變形性態進行預測分析。

1 變形監測數據的混沌特性識別

根據混沌理論，大壩變形監測數據是否具有混沌特性，首先要對數據序列進行相空間重構，然后可從數據的相空間中吸引子是否具有自相似結構的分數維幾何體以及數據對于初始狀態的條件是否十分敏感兩個基本特征判別[2]。前者通常采用關聯指數飽和法診斷是否存在分數維；后者采用最大的Lyapunov指數是否大于0進行判斷。本文選取最大的Lyapunov指數來確定數據序列的混沌特性。

1.1 重構相空間

在大壩變形數據的時間序列分析中，影響因素復雜眾多，其形成的動力學方程是非線性且混沌的。根據Takens定理，通過相空間重構能將混沌時間序列擴展到三維甚至更高維的相空間中，在拓撲變換的意義下恢復原系統的動力學特性，從而可以對系統的發展趨勢做出預測[3]。目前，重構相空間通常采用坐標延遲法，把一維變形監測的時間數據序列嵌入到維相空間中[4]：

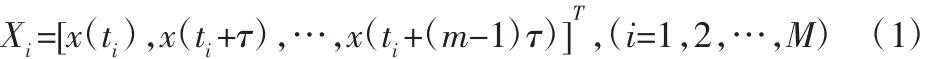
式中：τ=kΔt為時間延遲，k（k=1，2，…，n）為延遲參數，Δt為采樣間隔時間；m為嵌入維數；Xi為m維相空間中的相點；M=n-（m-1）τ為相點個數。

由上分析可知，相空間重構質量的好壞取決于重構參數的合理確定，自相關法對延遲時間的確定，以及采用G-P算法確定嵌入維數是討論的重點。

1.2 嵌入維數的計算

G-P算法最初是由Grassberger和Procaccia提出的，可用于時間序列數據的維數計算[4]。其主要計算步驟為：

1）利用自相關法確定延遲時間τ后，先假定一個值m0（通常比較小），構造一個重構的相空間；

2）通過此重構的相空間計算關聯維數C（λ）：

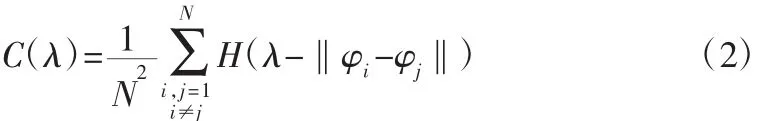
3）當處于某一特定范圍時，混沌吸引子的維數與之間有如下對數線性關系：于是可得 m0的維數 d（m0）；

4）重復以上步驟，隨著嵌入維數m的增大，在給定誤差范圍內，d（m）不再隨m的增大而發生較大的變化時為止，此時的m即為所求的嵌入維數。

1.3 最大Lyapunov指數的估計

Lyapunov指數是刻畫耗散體系相空間中相體積收縮過程中的幾何特征變化的物理量。Lyapunov指數表示為初值不同的兩條相鄰軌跡在相空間中隨時間推移按指數規律分離的平均發散速率，以定量描述混沌運動初值敏感程度[5]。Wolf[6]認為，對動力系統混沌運動進行判斷時，可等價于計算最大Lyapunov指數；若最大Lyapunov指數大于0，表明系統對初值敏感，可判定其運動為混沌狀態。

針對最大Lyapunov指數，可由Rosenstein等提出的算法進行計算，該算法對延遲時間、數據長度和噪聲的變化等具有較好的魯棒性[7]。其主要步驟如下：

1）根據延遲時間、嵌入維和式（1）重構相空間；

2）設為不同軌跡上相鄰兩點之間的距離，則：

式中，C為初始分岔。

找出相空間中一點 X（j）的鄰近點 X（j^），則：

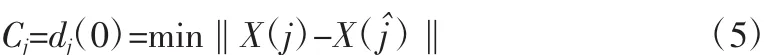
3）對相空間中的每一點X（j），計算出該鄰近點對的第個離散時間步的距離：

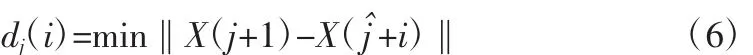
4）lndj（i）-iΔt曲線的斜率便是λ1，即：

式中，〈·〉表示為對所有j求平均。于是，可得最大Lyapunov指數λ1。

2 統計模型與混沌優化BP神經網絡融合預測模型

2.1 統計模型

目前，大壩效應量的安全監控模型通常基于壩工理論和數理統計方法采用統計模型、確定性模型和混合模型[8]。大壩監測效應量主要受到庫水壓力、溫度與時效等因素的影響，且影響因素直接互饋作用明顯，使得模型建立的精度不高。

通常，混凝土壩的變形按其成因主要由三部分構成：水壓因子（δH）、溫度因子（δT）和時效因子（δθ），即：

混凝土重力壩的統計模型可表示為：

式中，a0為常數項；ai為水壓因子回歸系數；H為壩前水深；bi為溫度因子回歸系數，c1，c2為時效因子回歸系數；θ=t/100，t為監測日到基準日的累積監測天數。

2.2 BP神經網絡預測模型

BP神經網絡主要由輸入層、隱含層和輸出層構成的一種多層前饋神經網絡，該網絡的主要特點是信號的正向傳遞和誤差反向傳播[9]。通過對神經網絡的輸入輸出參數的學習，達到表達函數非線性映射關系的目的。

當采用BP神經網絡來預測混沌時間序列時，若一個混沌時間序列的輸入為Xi=[x（ti），x（ti+τ），…，x（ti+（m-1）τ）]T，輸出為，可選擇BP神經網絡拓撲結構如圖1所示。

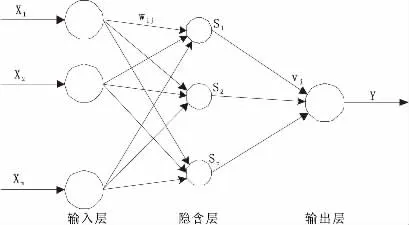
圖1 BP神經網絡拓撲結構圖

BP神經網絡隱含層各節點的輸入為：

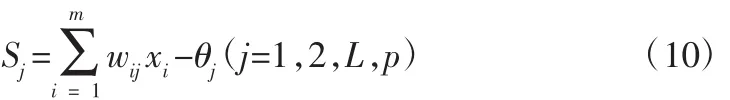
式中，wij為輸入層至隱含層的連接權重；θj為隱含層節點的閾值。

BP神經網絡隱含層的激勵函數有多種表達形式，在此采用Sigmoid函數f（x）=1/（1+e-x），則隱含層節點的輸出為：

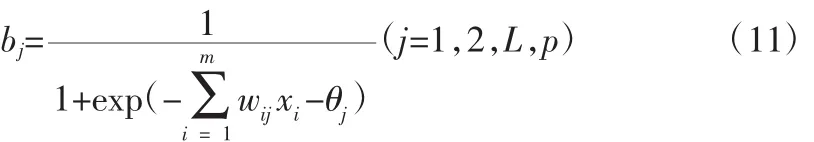
同理，輸出層節點的輸入、輸出分別為：

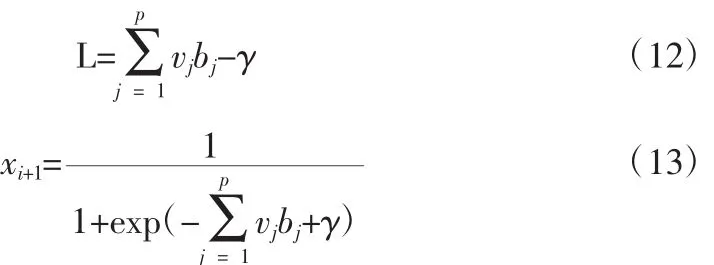
式中，vj為隱層至輸出層的連接權值，γ為輸出層的閾值。

通過BP神經網絡訓練求得連接權重wij、vj和閾值θj、γ，最終由式（13）獲得模型的預測值。

2.3 統計模型與BP神經網絡融合預測模型

統計模型基于壩工理論考慮了變形效應量的物理成因，BP神經網絡只是對于非線性函數擬合提供一種智能算法，并未考慮大壩變形觀測數據的混沌特性。因此，基于統計模型分離后的變形數據殘差序列進行混沌特性識別，對帶有混沌特性的數據序列來構建混沌優化BP神經網絡融合模型進行大壩變形預測。其主要建模步驟如下：

step1：對變形數據進行統計建模，根據式（9）進行回歸計算，可獲得統計模型的擬合值、預測值和殘差值；

step2：針對變形殘差時間序列數據，采用G-P算法、自相關法計算得到的嵌入維數、延遲時間將一維變形時間序列重構為多維相空間，建立混沌優化BP神經網絡預測模型；

step3：混沌優化BP神經網絡創建并訓練后，得到殘差序列的預測值，并與統計模型預測值融合得到模型最終預測值。

3 工程實例

以某碾壓混凝土重力壩的3#壩段測點水平位移的監測數據為分析對象，選取1010個大壩變形監測時間序列數據作為建模的樣本數據，其中將前1000個數據作為訓練集，剩下10個數據作為測試集，建立大壩變形統計模型與混沌優化BP融合預測模型，見圖2。

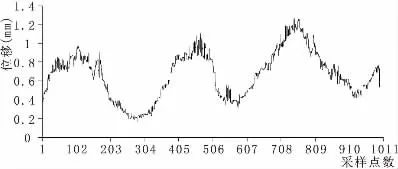
圖2 大壩測點水平位移方向實測過程線

3.1 模型計算

將訓練集的變形監測數據用式（9）建立統計模型，并用統計模型預測測試集的數據，其結果見圖3和圖4。

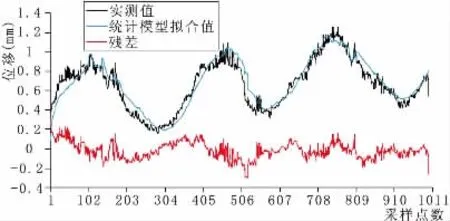
圖3 訓練集的實測、擬合及殘差曲線

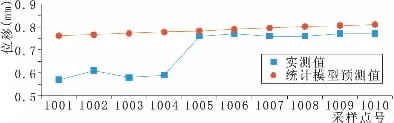
圖4 測試集的實測與統計模型預測值

關于殘差時間序列數據，根據自相關法確定延遲時間為τ=10，并采用G-P算法得到m=7，據此重構相空間。

由式（7）計算得到訓練集數據的最大Lyapunov指數λ1=0.0182，可知該訓練集的殘差時間序列數據具有混沌特性，此時選取的測試集長度為10在允許最大預測時間為1/λ1≈55之內，可進行測試集數據趨勢的預測。

3.2 預測結果及性能評價

由組合模型的建模步驟，在MATLAB中編制程序訓練，得到BP神經網絡的輸出。則統計模型與混沌優化BP模型的預測值，具體結果見圖5。

圖5 測試集T的實測值、組合模型預測值和殘差值

為對模型進行性能評價，選用δMAE，δMSE，R作為定量評價指標。

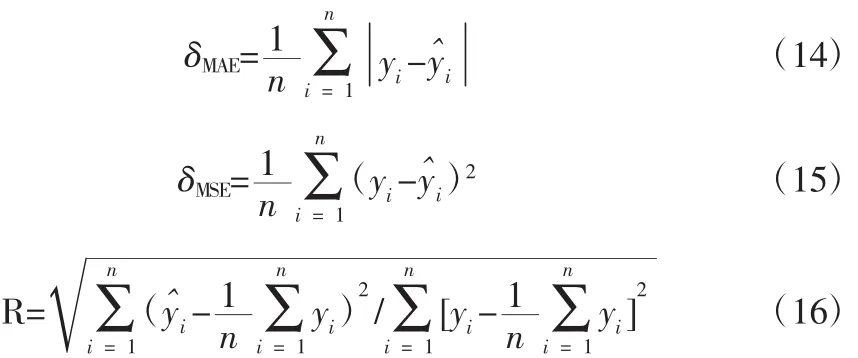
式中，yi為實測值；為預測值。

將統計模型與混沌優化BP神經網絡融合建模與傳統的統計模型進行比較，從表1可以看出，統計模型-混沌優化BP的預測精度優于傳統統計模型的精度。

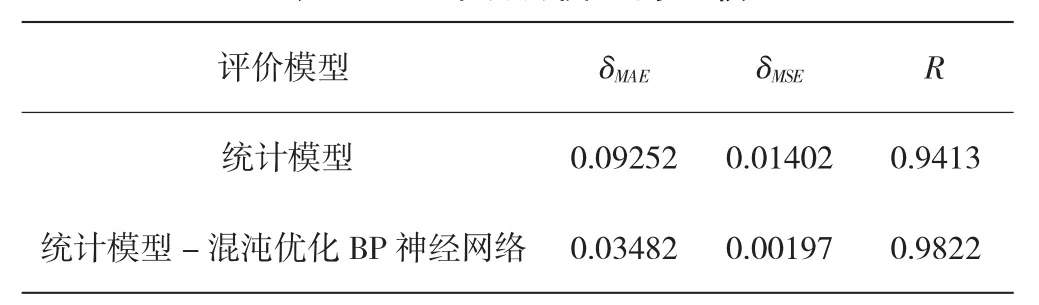
表1 兩種預測模型的比較

4 結論

（1）根據混沌理論，將大壩的水平位移看成時間序列，進行相空間重構用Rosenstein算法計算得到了實測序列最大Lyapunov指數為正數，可判斷系統存在混沌成分。

（2）基于統計模型的不足，通過對大壩變形監測數據統計模型的殘差序列進行混沌特性分析，建立了統計模型與混沌優化BP神經網絡變融合的預測模型。將該預測模型運用于具體工程實例，表明模型具有比較好的預測效果，可滿足實際工程的需要，值得推廣。