直流不間斷電源雙向DC－DC變換器非線性現象分析

李紅麗，王立華，倪 雪，張 瑞

（1.西安電子科技大學 通信工程學院，陜西 西安710071；2.山東科技大學 電子通信與物理學院，山東 青島266590）

0 引 言

雙向DC－DC變換器是直流不間斷電源UPS（Uninterruptible Power Supply）的重要組成部分［1］。雙向DC－DC變換器屬于強非線性系統，當電路參數發生變化時，系統可能會產生不規則行為，例如分岔和混沌現象［2］。因此，明確雙向DC－DC變換器出現分岔或混沌的時間以及原因，對于改進系統設計，進行新型有效控制，實現現有雙向DC－DC變換器無法達到的性能具有重要意義［3］。

目前對于雙向DC－DC變換器的研究主要集中在電路拓撲和控制［4］兩個方面，對于混沌特性方面的研究較少［5］。本文以雙向Buck－Boost變換器為研究對象，利用分岔圖［6］、時域波形圖、相圖等方法以及 Matlab／Simulink工具，著重研究其非線性現象。由于雙向DC－DC變換器在單向DC－DC變換器的基礎上形成，因此兩者在混沌的分析與控制上有很大關聯，但是與單向DC－DC變換器主要的不同是，由于雙向DCDC變換器屬于共用電路，因此電路中的電感參數值唯一，在進行分析與設計時需更合理的調整各種參數值來達到理想效果。

1 雙向DC－DC變換器控制與仿真建模

雙向DC－DC變換器主電路拓撲結構如圖1所示。

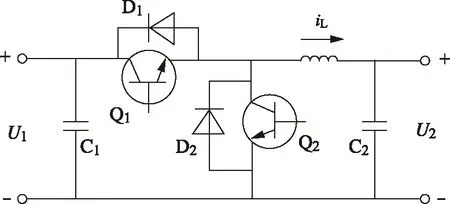
圖1 雙向DC－DC變換器主電路拓撲結構

雙向 DC－DC變換器有三種工作方式［7］：Buck工作方式，Boost工作方式以及交替工作方式，交替工作方式相當于短時間內的Buck工作方式與Boost工作方式的交替，因此主要研究前兩種工作方式。另外，Q1和Q2為互補PWM工作，即Q1導通時Q2截止，Q2導通時Q1截止，電感電流iL始終為三角波，不會出現單向DC－DC變換器中在一段時間內會出現iL＝0的電流斷續情況，這是雙向與單向DC－DC變換器的又一不同之處。

采用雙閉環控制的形式，Buck工作方式下通常采用電壓反饋控制，Boost工作方式下采用電流反饋控制，如圖2（a）、（b）所示。在電路中加入判斷電路，若iL＞0，則處于Buck工作方式，選擇圖2（a）控制電路；若iL＜0，則處于Boost工作方式，選擇圖2（b）控制電路。

圖2 雙向DC－DC控制電路

下面分別建立Buck工作方式以及Boost工作方式下的狀態方程。對于Buck工作方式，根據KCL和KVL，選取電容C2兩端電壓U2和流過電感電流iL作為兩個狀態變量，設開關Q1導通為狀態1，開關Q1關斷為狀態2。

（1）狀態1：

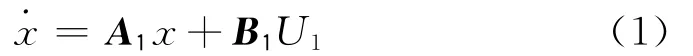
（2）狀態2：

式中，狀態變量x＝［Uo，iL］T，Uo＝U2。A1，A2，B1，B2為狀態矩陣。

引入積分因子1／s，可得數學表達式：

（1）狀態1：

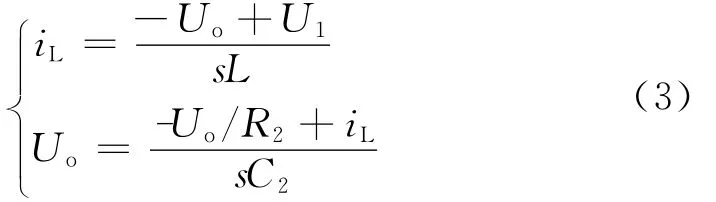
（2）狀態2：

引入開關函數δ，可得到統一表達式。δ是一個調制信號，當Uc（t）＞Ur（t）時，δ＝0；當Uc（t）＜Ur（t）時，δ＝1。則統一表達式為：

同樣的，可以求得Boost工作方式下的狀態方程為：

式（6）中Uo＝U1；δ是一個調制信號，當開關 Q2導通時，δ＝0；當開關Q2關斷時，δ＝1。

利用式（5）和式（6），在 Matlab／Simulink環境中搭建分段開關模型并進行仿真，如圖3所示。

圖3 雙向DC－DC分段開關模型

假設電路的各組成部分均為理想器件，雙向DCDC變換器的參數值如表1、2所示。

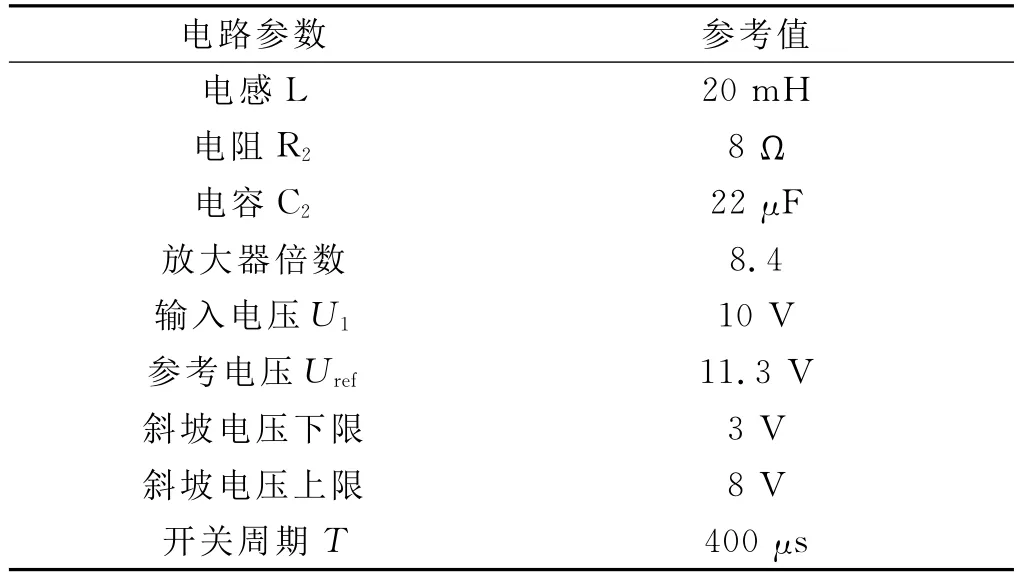
表1 Buck工作方式下電路參數值表

表2 Boost工作方式下電路參數值表

2 雙向DC－DC非線性行為分析

2.1 雙向DC－DC非線性行為理論分析

根據控制電路，可以得出在Buck工作方式下輸入電壓U1以及在Boost工作方式下參考電流iref的變化對雙向DC－DC的非線性行為影響較大，因此分別選取輸入電壓U1和參考電流iref作為分岔參數，得到在Buck以及Boost工作方式下電感電流iL的分岔圖，如圖4（a）、（b）所示。

圖4 雙向DC－DC分岔圖

從圖4（a）中可以看出，Buck工作方式下隨著輸入電壓U1的改變，電感電流iL呈現不同的表現。當U1約為26 V時，系統出現分岔，從單周期進入二倍周期。當U1約為31 V時，系統再次出現分岔，從二倍周期進入四倍周期。當U1增大到約32 V時，系統進入混沌狀態。

從圖4（b）中可以看出，Boost工作方式下隨著參考電流iref的改變，電感電流iL呈現不同的表現。當iref約為0.7 A時，系統出現分岔，從單周期進入二倍周期。當iref增大到約1.3 A時，系統進入混沌狀態，其四倍周期表現不明顯。

2.2 雙向DC－DC非線性行為仿真驗證

對分段開關模型進行仿真，分別通過改變輸入電壓U1和參考電流iref的大小，并保持其他參數不變，觀察電感電流iL和輸出電壓Uo的變化。其中Buck工作方式下的仿真結果如圖5～圖8所示。

圖5 U1＝18 V，雙向DC－DC單周期行為圖

由圖5可知，當輸入電壓U1＝18 V時，電感電流iL是一個穩定的鋸齒波，輸出電壓Uo是一個穩定的正弦波，其波形是周期的，相圖只有一個環，因此可以判斷變換器運行于單周期軌道。

圖6 U1＝25 V，雙向DC－DC二倍周期行為圖

由圖6可知，當輸入電壓U1＝25 V時，電感電流iL和輸出電壓Uo的波形出現了分岔，但仍是周期的，相圖也出現了分岔，可以判斷變換器運行于二倍周期軌道。

圖7 U1＝31 V，雙向DC－DC四倍周期行為圖

由圖7可知，當輸入電壓U1＝31 V時，電感電流iL和輸出電壓Uo出現三個峰值，相圖為兩個極限環，可以判斷變換器運行于四倍周期軌道。

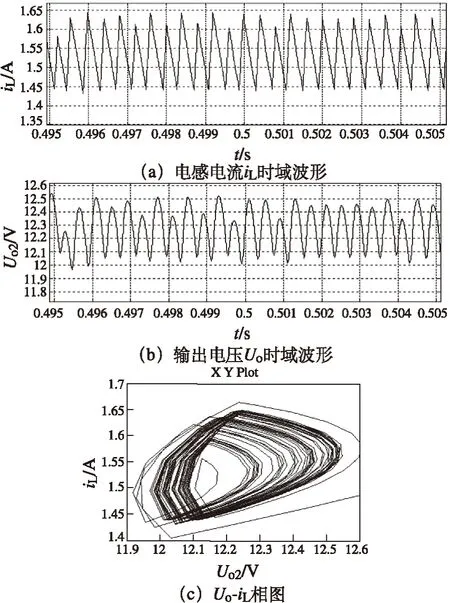
圖8 U1＝50 V，雙向DC－DC混沌行為圖

由圖8可知，當輸入電壓U1＝50 V時，電感電流iL和輸出電壓Uo的波形變得雜亂，無周期可言，相圖變得不可預測，可以看出變換器已進入混沌狀態。

Boost工作方式下的仿真結果如圖9～圖11所示。

圖9 iref＝0.4 A，雙向DC－DC單周期行為圖

由圖9可知，當參考電流iref＝0.4 A時，電感電流iL和輸出電壓Uo的波形比較規整，周期為100μs，與設置的開關周期一致，并且相圖由有限封閉曲線構成，只有一個環，因此可以判斷變換器運行于單周期軌道。

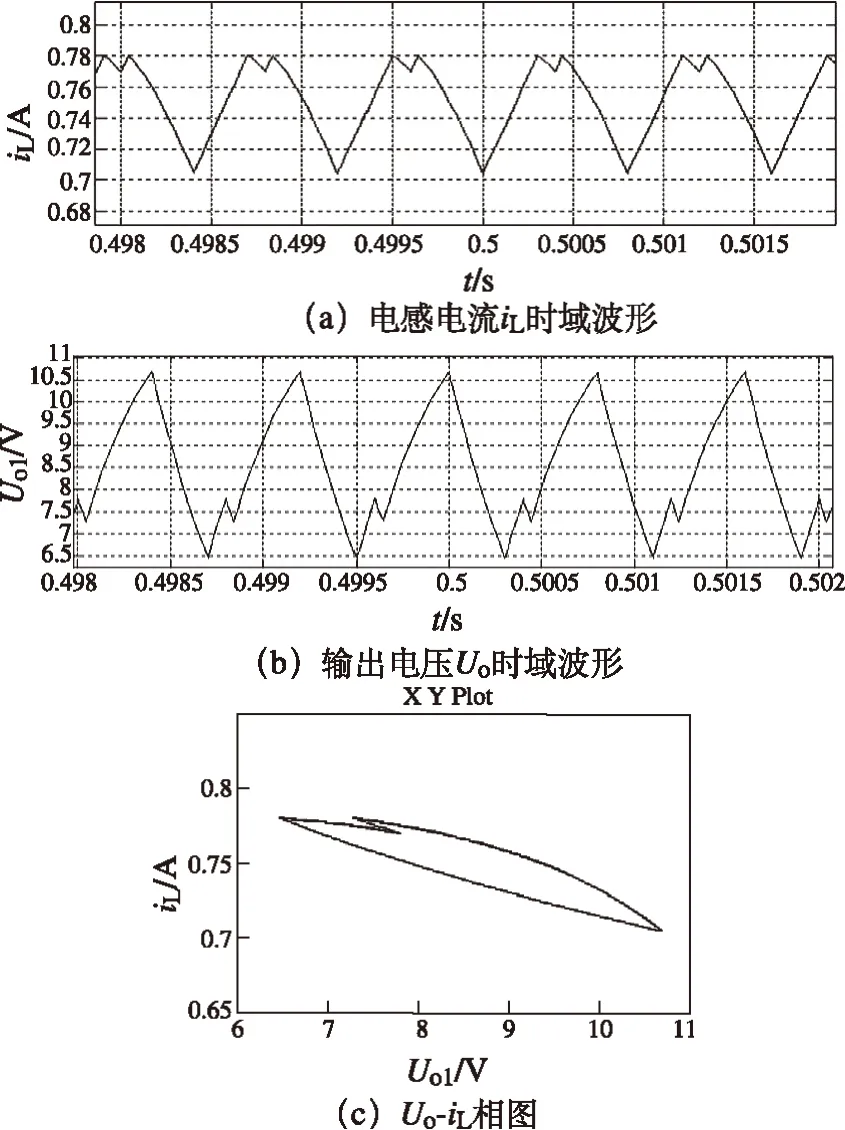
圖10 iref＝0.78 A，雙向DC－DC二倍周期行為圖

由圖10可知，當參考電流iref＝0.78 A時，電感電流iL和輸出電壓Uo的波形出現了分岔，但仍是周期的為200μs，是開關周期的2倍，相圖也出現了分岔，可以判斷變換器運行于二倍周期軌道。

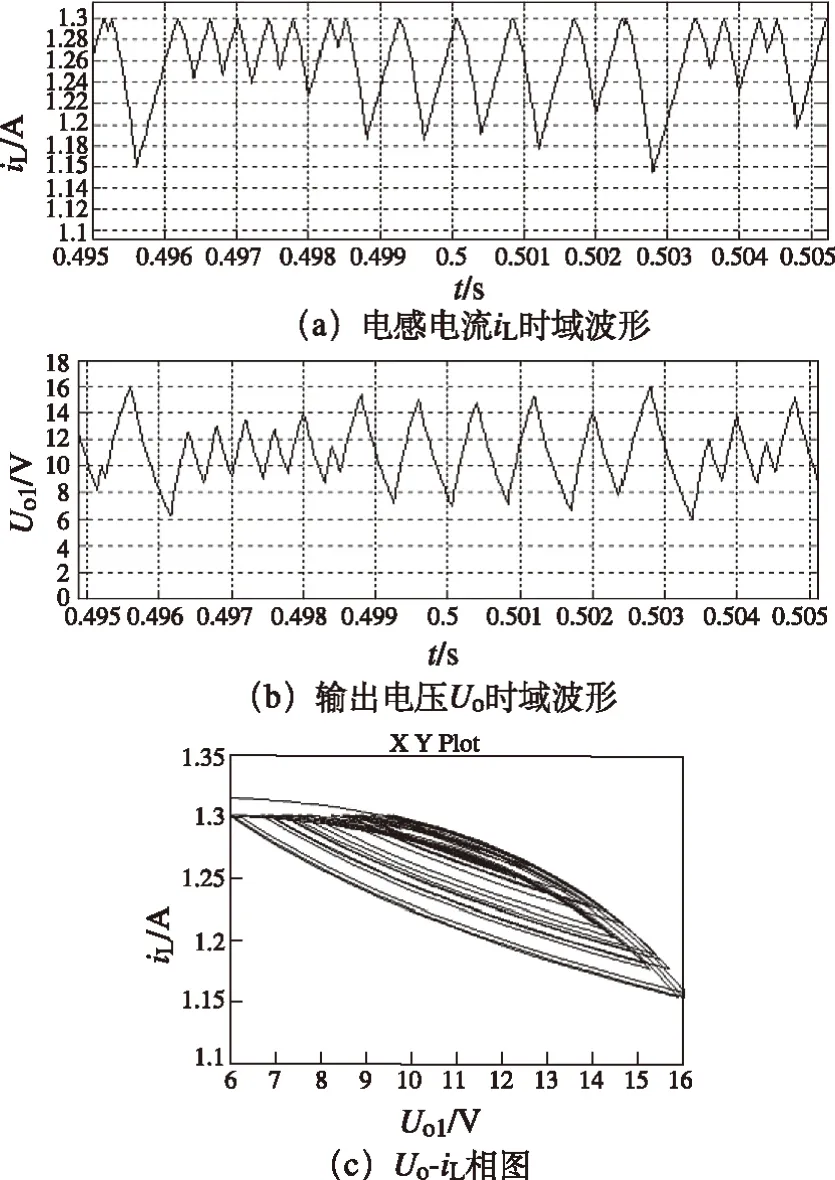
圖11 iref＝1.3 A，雙向DC－DC混沌行為圖

由圖11可知，當參考電流iref＝1.3 A時，電感電流iL和輸出電壓Uo的波形變得雜亂，無周期可言，相圖變得不可預測，可以看出變換器已進入混沌狀態。

3 結 論

本文對直流不間斷電源中雙向DC－DC變換器進行了深入研究，討論了其非線性特性，通過對給定參數值的雙向DC－DC變換器的仿真、分析與驗證，得出以下結論：

（1）Buck工作方式下，系統隨輸入電壓U1的改變而發生變化：U1約為26 V時，系統從單周期進入二倍周期；U1約為31 V時，系統從二倍周期進入四倍周期；U1增至約32 V時，系統進入混沌狀態。

（2）Boost工作方式下，系統隨參考電流iref的改變而發生變化：iref約為0.7 A時，系統從單周期進入二倍周期；iref增至約1.3 A時，系統進入混沌狀態；其四倍周期表現不明顯。