考慮航空發動機支承不同心的整機動力學建模及分析

吳英祥，張亞雙，陳 果

（1.中國航發沈陽發動機研究所，沈陽110015；2.中國航發沈陽黎明航空發動機有限責任公司，沈陽110043；3.南京航空航天大學民航學院，南京210016）

0 引言

同心度是對航空發動機整機振動響應有重要影響的參數，在發動機裝配過程中，必須進行嚴格控制[1]。航空發動機不同心主要包括轉子、支承和轉靜子不同心[2]。轉子不同心將引發較大的不平衡響應，轉靜子不同心可能引發碰摩故障，二者的故障機理比較清楚，但是支承不同心故障機理尚不清楚。張振波等[3]建立了適應航空發動機柔性轉子系統在不同心和不平衡激勵作用下的動力學模型，研究了帶有支承不同心的轉子動力學響應問題。馮國全等[4]基于某航空發動機轉子系統，建立了考慮支撐軸承不對中的內外雙轉子系統動力學模型，分析了低于和高于第1階臨界轉速的情況，結果表明，內外轉子的振動均出現2倍頻成分，且隨著不對中程度的加大，2倍頻成分也明顯增大且會占主導，軸心軌跡會從近似圓形變化為8字形。Xu M等[5-6]分析了柔性電機的不對中和不平衡故障機理，并采用試驗方法進行了驗證。Al-Hussain K M[7]和Lees A W[8]研究了剛性聯軸器的不對中故障特性。李明[9]建立了1個平行不對中轉子系統的動力學模型，研究了平行不對中轉子系統的非線性動力學特性。長期以來，人們普遍認為支承不同心將引發轉子不對中，導致用聯軸器連接的2個轉子形成平行不對中和角度不對中，最終在聯軸器兩端形成附加力和力矩，從而引發轉子系統振動，進而對發動機整機振動產生影響，并且認為不對中故障的特征之一是出現較大的2倍頻[10]。在航空發動機實際工作中，支承不同心基本控制在數十微米，可以通過軸承間隙來補償，裝配完成后不會產生較大的附加力矩；但如果控制不嚴格，數十微米的支承不同心也會產生較大的整機振動和軸承損壞。現有的轉子不對中和軸承不對中模型難于解釋數十微米支承不同心所引發的整機振動問題。

因此，深入研究支承不同心對航空發動機整機振動的影響機理及有效控制發動機整機振動具有重要意義。本文將支承不同心轉化為軸承間隙，并將模型導入整機模型進行耦合動力學仿真，研究了由于支承不同心所引發的整機振動問題，并以某型雙轉子渦扇航空發動機為例進行仿真分析。

1 支承不同心模型

支承不同心的縱剖面和橫截面模型如圖1所示。圖1（b）為支承不同心下的滾動軸承作用力模型，其中O1為支承原始中心，O2為支承不同心后的支承處轉子軸心。設：c為軸承間隙，xr、yr分別為轉軸的x向和y向位移，xB、yB分別為軸承座的x向和y向位移，x0、y0分別為支承x向和y向的不同心量。位移r為轉軸與軸承間的徑向相對位移，其表達式為

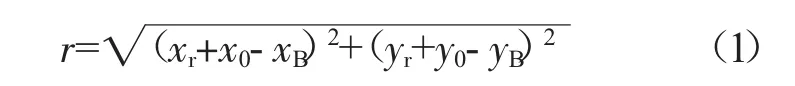
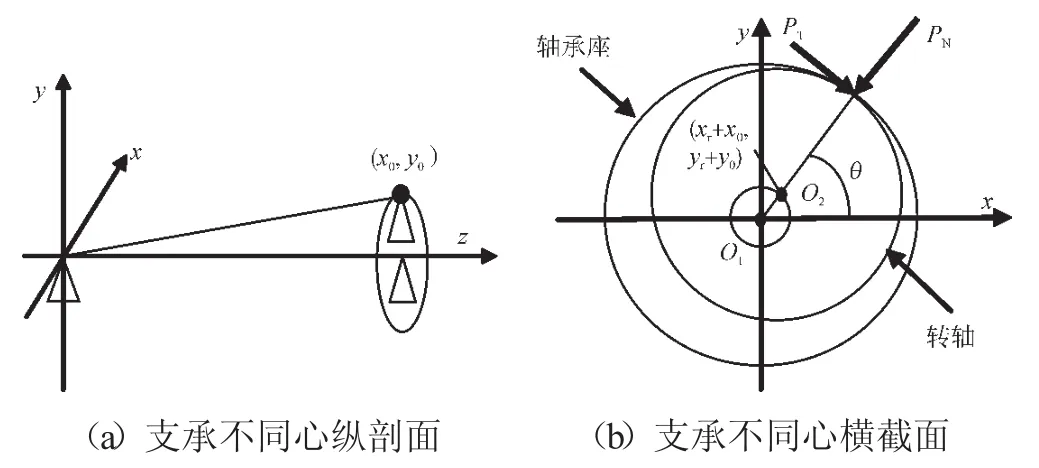
圖1 支承不同心模型

當r＜c時，不發生接觸；當r≥c時，發生接觸。假設摩擦符合庫侖摩擦定律，則軸承接觸后產生的法向力和切向力摩擦力為

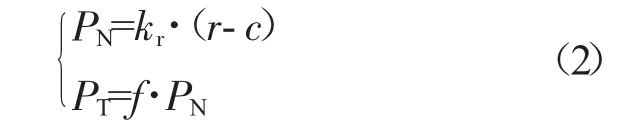
式中：kr為軸承徑向剛度；f為摩擦系數。需要注意的是，切向摩擦力需要根據軸承外圈和軸承座之間的相對運動速度方向來判斷。將法向和切向作用力分解在x軸和y軸

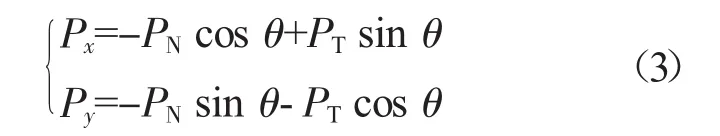
另外，滾動軸承外圈通常需要利用鎖緊螺母鎖緊。在擰緊螺母壓力作用下，當外圈與軸承座存在相對運動時，外圈與鎖緊螺母內表面將產生摩擦效應，該摩擦效應主要表現為干摩擦阻尼效應，而軸承擰緊力矩將改變接觸面間的摩擦力，從而改變摩擦阻尼，不失一般性，為了簡化研究，本文將摩擦阻尼等效為黏性阻尼。

2 發動機支承不同心建模分析

某型雙轉子航空渦扇發動機支承形式如圖2所示。從圖中可見，該型發動機低壓轉子采用1-2-1型支承方式，支承1位于低壓壓氣機之前，支承2、3位于低壓壓氣機和低壓渦輪之間，支承5位于低壓渦輪之后。低壓壓氣機轉子與低壓渦輪轉子采用柔性聯軸器聯接，傳遞扭矩和軸向力。高壓轉子采用1-0-1型支承方式，支承3位于高壓壓氣機之前，支承5位于高壓渦輪之后。

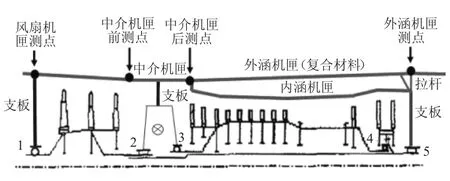
圖2 某型雙轉子航空發動機支承結構

對于該轉子系統，支承1、2支承低壓壓氣機轉子，位于風扇前后，跨度較短，且均支承在同一段機匣上，其同心度易于保證。支承5位于低壓渦輪之后，跨度較大，且支承5處于高溫環境中，其同心度往往很難保證。高壓轉子后支承為中介軸承支承（圖2中的支點4），支承在低壓轉子上，因此，高壓轉子支承的同心度需要通過支承3、5的同心度反映。綜上所述，在該型發動機上重點關注的支承不同心主要為：支點2、5，其不同心模型如圖 3所示；支點 3、5，其不同心模型如圖4所示。

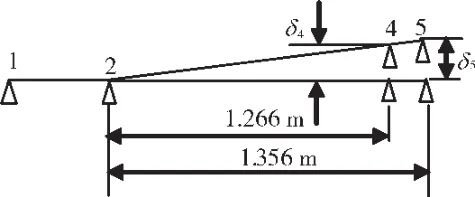
圖3 低壓轉子支承2-5的不同心度模型

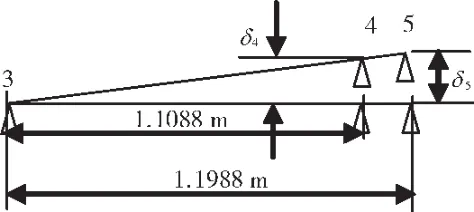
圖4 高壓轉子支承3-5的不同心度模型

從圖3中可見，當低壓轉子支點12-5不同心時，支點5的不同心量為δ5，則支點4對應的內轉子不同心量為δ4。支點4和5的距離很近，在低壓轉子支承2-5不同心模型中，δ4=0.93δ5；在高壓轉子支承 3-5不同心模型中，δ4=0.92δ5。

在出現低壓轉子支承2-5不同心（圖3）和高壓轉子支承3-5不同心（圖4）時，為了能夠實現高、低壓轉子的裝配，必須要調整支點4和5的滾動軸承徑向間隙，否則，轉子將承受由不同心產生的附加力矩，從而使轉子產生初始彎曲變形。事實上，由于航空發動機是高精度旋轉機械，其不同心量很小，通過調整滾動軸承間隙即可實現不同心量的補償。在該假設前提下，顯然不同心量的大小將直接影響滾動軸承間隙的大小，而航空發動機支承不同心下的整機振動響應和軸承載荷也與滾動軸承間隙大小息息相關。

本文通過數值仿真計算來分析低壓轉子支承2-5不同心度和高壓轉子支承3-5的不同心度對航空發動機整機振動的影響。在同心度模型中，將不同心度等效為支點4、5的滾動軸承間隙。

3 含支承不同心的發動機整機振動建模

3.1 發動機整機振動模型

航空發動機整機振動建模包括轉子系統有限元模型、機匣有限元模型、支承集總參數模型，是混合動力學模型，該方法運用Newmark-b法和翟方法相結合進行時域數值積分求解，可以高效地求解系統非線性響應[11-12]。

3.1.1 轉子系統運動方程

將轉子考慮為由若干支承和轉盤組成的系統。轉子利用有限元方法離散為普通梁單元，考慮轉子系統的剪切變形、陀螺力矩和轉動慣量。將單元的運動方程進行組裝，得到轉子系統運動方程

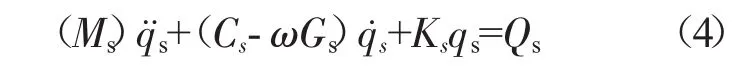
式中：Qs為系統廣義外力向量；Ms為系統質量矩陣；Gs為系統陀螺矩陣；Ks為系統剛度矩陣；Cs為系統阻尼矩陣，本文將Cs假設為比例阻尼。

3.1.2 機匣運動方程

將機匣按不旋轉的軸（梁單元結構）處理，也需考慮剪切效應和轉動慣量。因此，與轉子模型的處理方法相同，用有限元方法得到機匣的運動微分方程

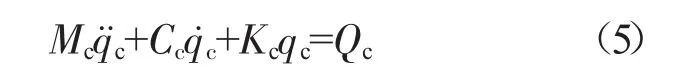
式中：Qc為機匣系統廣義外力向量；Mc為機匣系統質量矩陣；Kc為機匣系統剛度矩陣；Cc為機匣系統阻尼矩陣，同樣假設Cc為比例阻尼。

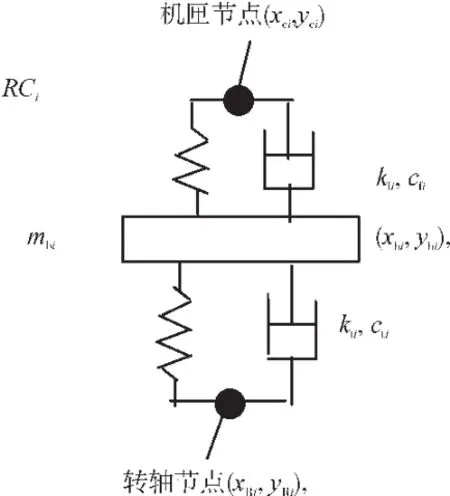
圖5 轉子-機匣支承

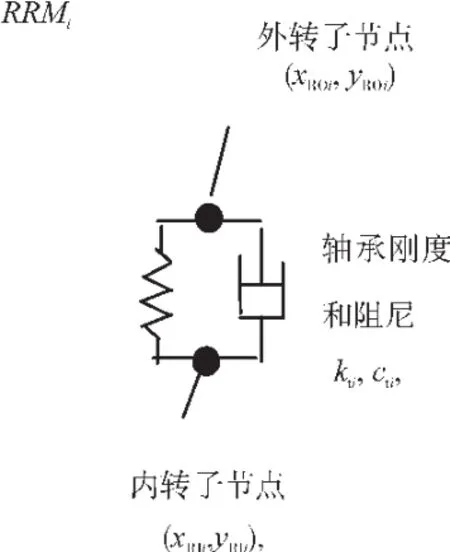
圖6 中介軸承支承

3.1.3 轉子-機匣間的支承連接

對于每個轉子與機匣間的支承RCi（i=1，2，…，N），包括滾動軸承、軸承座等部件，滾動軸承用線性彈簧模擬。其中，mbi為軸承座質量；kti為轉軸與軸承座之間的軸承彈性支承剛度，cti為對應的阻尼系數；kfi，cfi分別為機匣與軸承座之間的支承剛度和阻尼，如圖5所示。從圖中可見，kti為轉軸與軸承座之間的軸承等效剛度，由于支承不同心引起了軸承間隙的變化，因此軸承力表現為類似于轉靜碰摩的碰摩力。設軸承間隙為c，支承不同心量為x0和y0。轉子-機匣間的支承力（即支承RCi作用于轉子的力）為

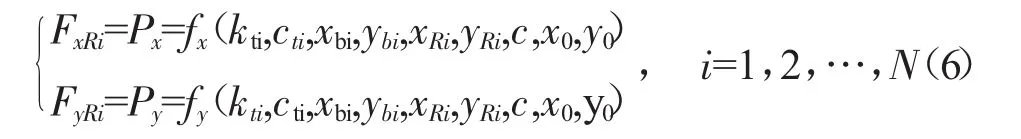
設機匣節點位移為xci和yci，支承RCi的軸承座的位移為xbi和ybi，則機匣作用于支承RCi的力為

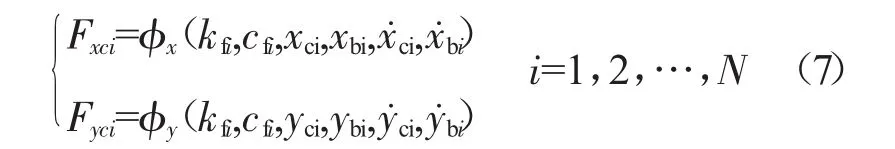
因此，支承RCi的軸承座的運動微分方程為

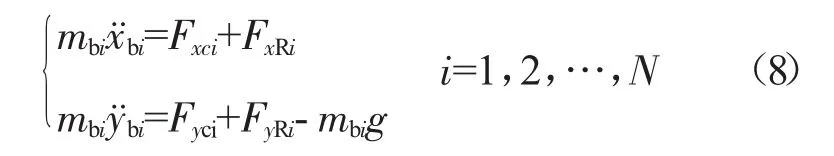
3.1.4 轉子-轉子間的中介軸承支承

對于每個轉子與轉子間的中介軸承支承RRMi（i=1，2，…，N），僅僅包括滾動軸承的支承剛度，如圖6所示。從圖中可見，kti為轉軸與軸承座之間的軸承等效剛度，由于支承不同心引起軸承間隙的變化，因此軸承力類似于轉靜碰摩的碰摩力。設軸承間隙為c，支承不同心量為x0和y0。轉子-轉子間的中介軸承支承力（即支承RRMi作用于內外轉子的力）為

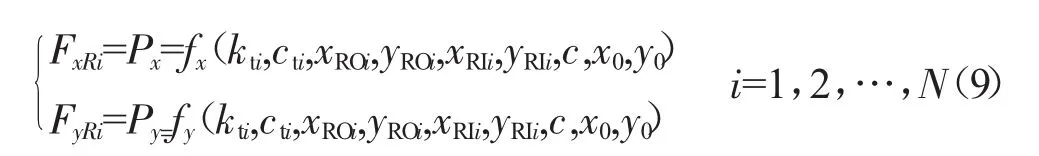
3.2 支承不同心的航空發動機整機振動分析

3.2.1 計算條件

3.2.1.1 高、低壓轉速變化關系

（1）低壓轉速 N1=0～3552 r/min，高壓轉速 N2=3N1；（2）N1=3552～8880 r/min，N2=0.77121N1+7826.6621。

3.2.1.2 不平衡量

考慮實際發動機的不平衡量分布：（1）第1、3級風扇葉片不平衡量為 100 g·cm；（2）第 4、9 級高壓壓氣機葉片不平衡量為127 g·cm；（3）第9級高壓壓氣機盤后1節點（蓖齒盤）和高壓渦輪葉片后1節點（修正面）不平衡量為 120 g·cm；（4）第 1、2 級低壓渦輪葉片不平衡量為250 g·cm。

3.2.1.3 不同心計算條件

不同心的計算條件見表1。考慮正常同心度的工況Case1下，滾動軸承的徑向間隙均設定為0 μm。在較大不同心度的工況Case2下，設定支點5軸承間隙為50 μm，支點4中介軸承間隙為45 μm。在更大不同心度的工況Case3下，設定支點5軸承間隙為100 μm，支點4中介軸承間隙為90 μm。

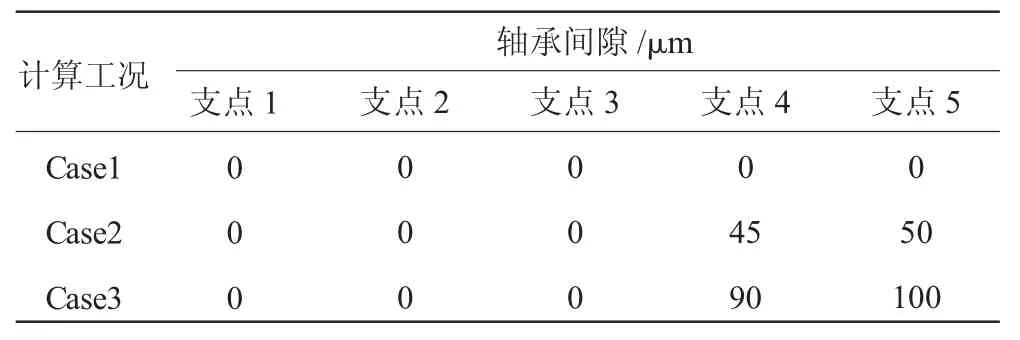
表1 支承不同心的計算工況

3.2.2 支承不同心的影響分析

分別對3種工況進行仿真計算，支承1、2、4、5處的軸承力和轉子節點的振動加速度的最大值比較分別如圖7、8所示，計算結果分別見表2、3；進氣機匣、中介前機匣、中介后機匣、渦輪機匣測點對應的節點力和振動加速度的最大值比較分別如圖9、10所示，計算結果分別見表4、5。

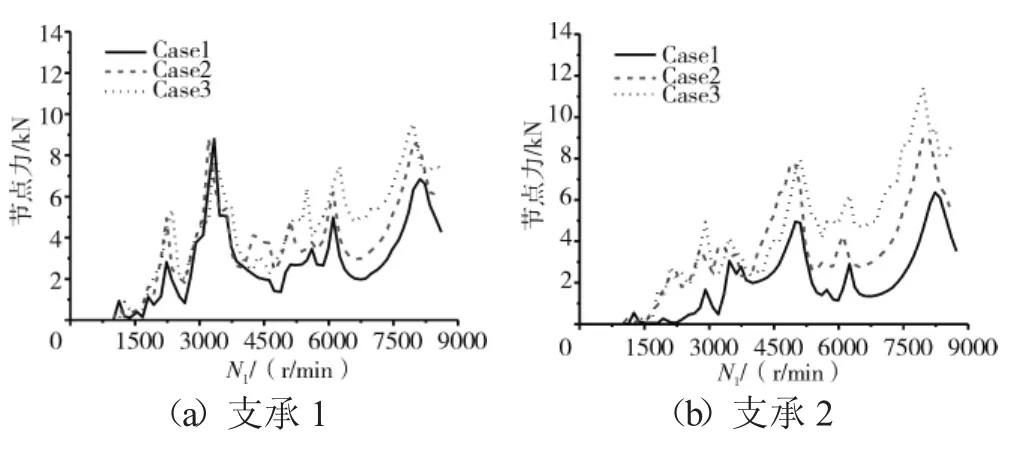
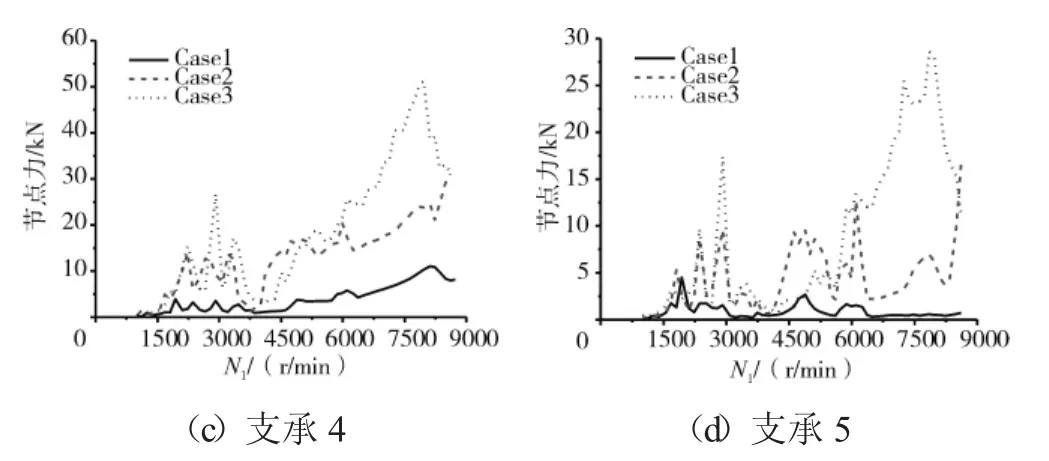
圖7 支承處轉子節點的軸承作用力

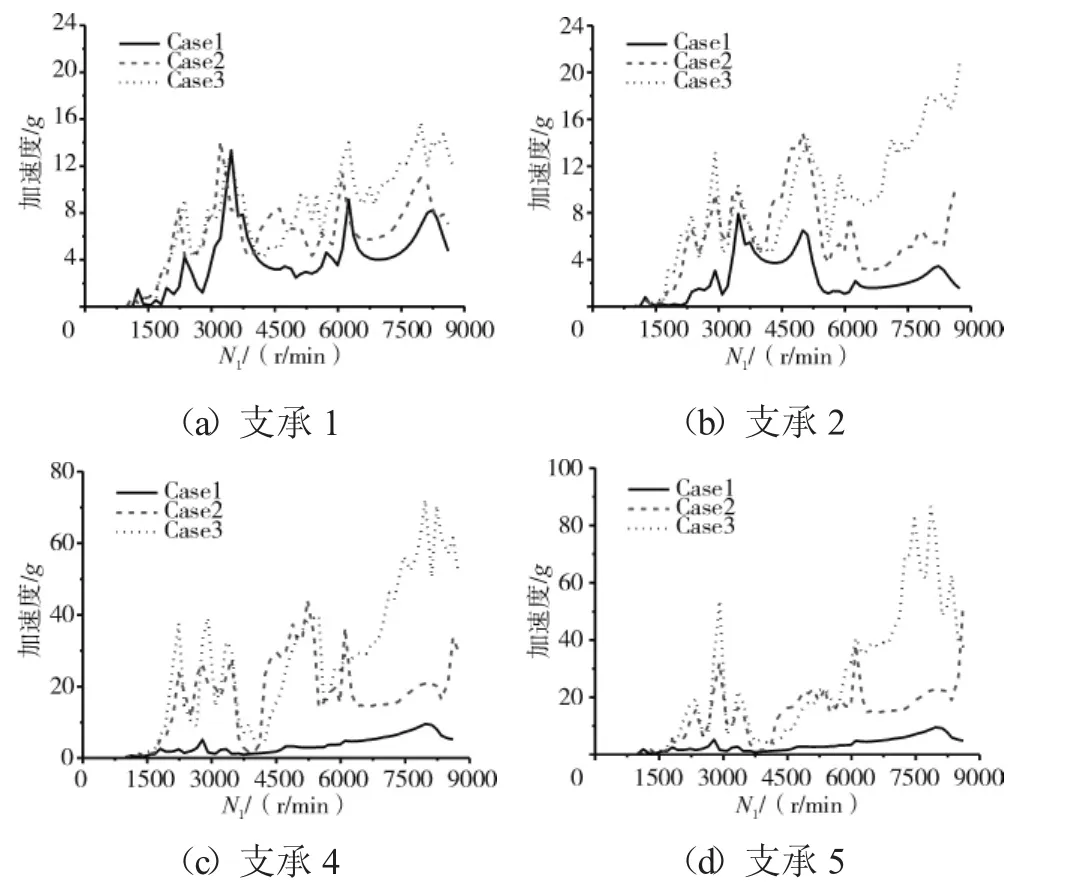
圖8 支承處轉子節點的振動加速度

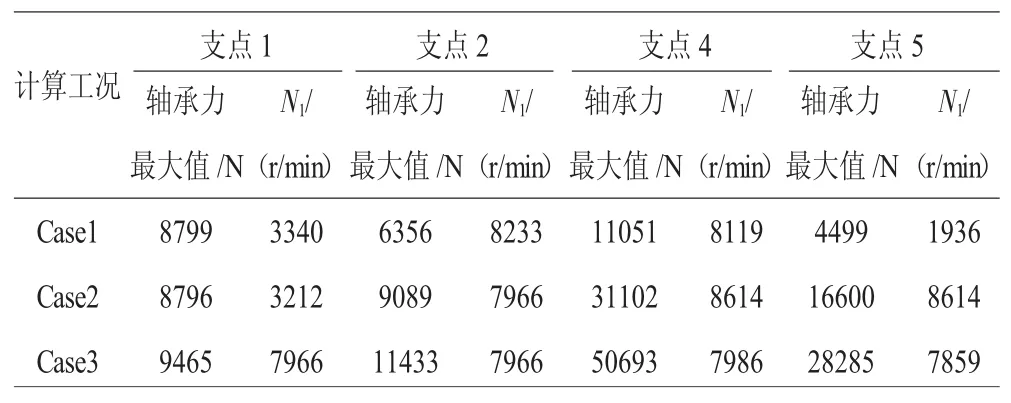
表2 支承軸承力計算結果比較

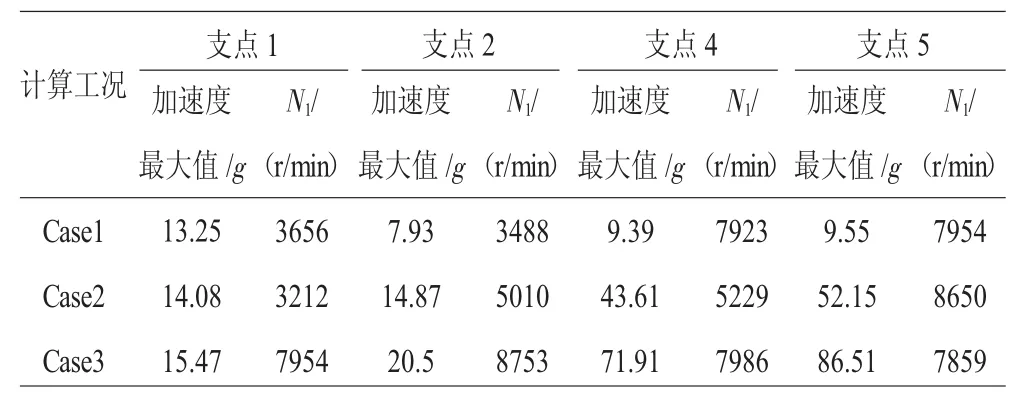
表3 支承處轉子節點加速度計算結果比較

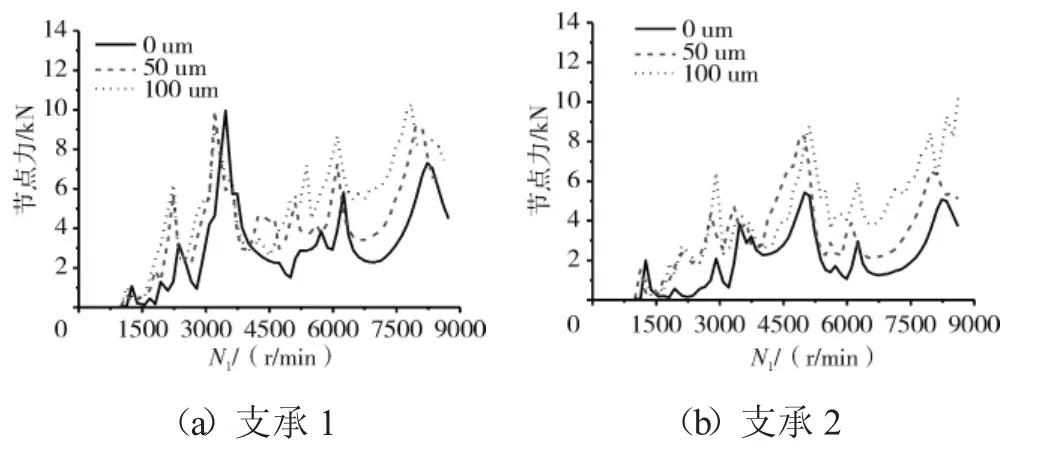
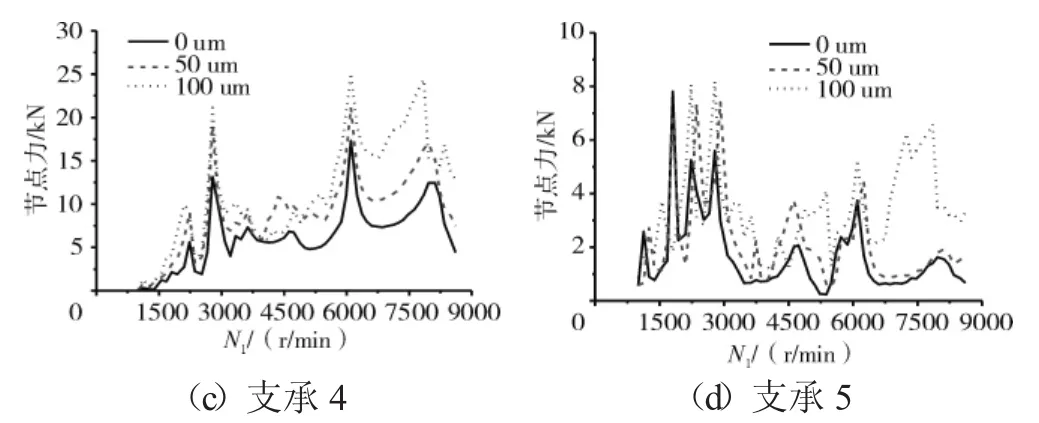
圖9 機匣測點對應的機匣節點力最大值隨N1的變化規律

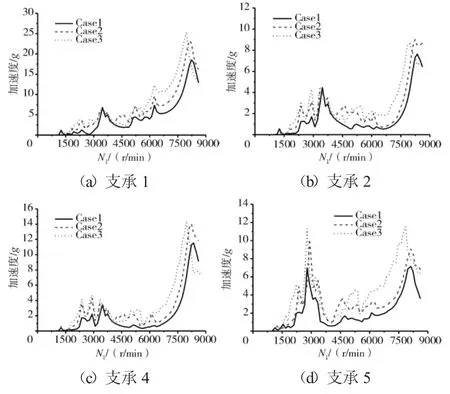
圖10 機匣測點加速度最大值隨轉速N1的變化規律

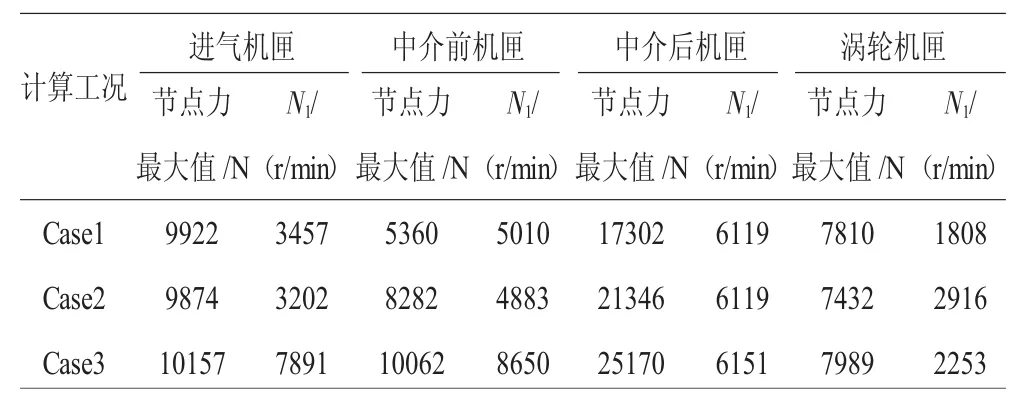
表4 機匣測點對應的機匣節點力計算結果比較

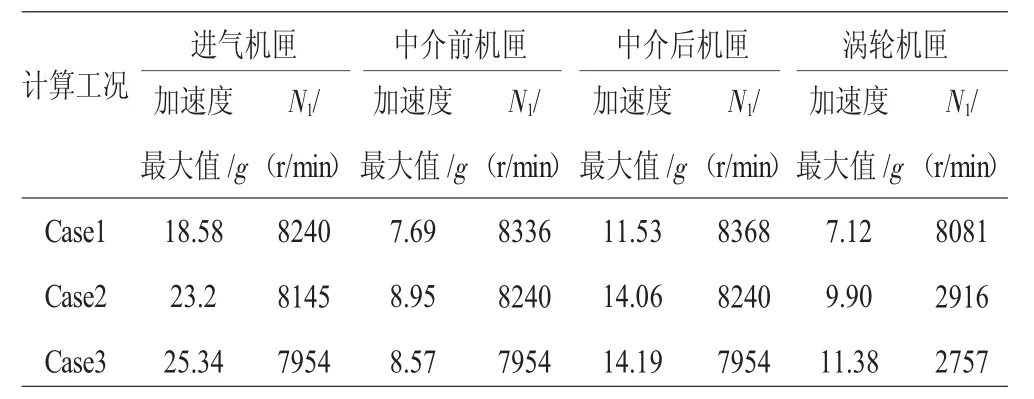
表5 機匣測點加速度計算結果比較

從圖7和表2中可見，支點4處的軸承力最大值，在Case1完全同心時僅為10 kN，隨著不同心度的增加，在中度Case2的不同心時達到30 kN，而在Case3的嚴重不同心時達到50 kN。支點5處的軸承力最大值，在Case1完全同心時僅為5 kN，在Case2時達到15 kN，而在Case3時達到30 kN。對于支承1和2，不同心度對其影響很小，軸承力隨著不同心的加劇增加不大。

從圖8和表3中可見，支點4處的轉子節點的振動加速度最大值，在Case1完全同心時僅為10g，隨著不同心度的增加，在Case2時達到40g，在Case3時達到70g。支點5處的轉子節點加速度最大值，在Case1時僅為10g，在Case2時達到40g，在Case3時達到90g。支承1、2對應的支承轉子節點振動加速度隨著不同心的加劇增加不大。

從圖9、10和表3、4中可見，隨著不同心的加劇，機匣測點的響應加速度和機匣節點力增加并不大，表明由不同心引發的軸承力傳遞到機匣時已經衰減許多，所以機匣測點加速度對不同心故障并不靈敏。

由此可見，過大的不同心盡管引起的機匣加速度并不大，但是導致軸承力很大，從而引起軸承加速磨損、疲勞破壞。其中支承不同心對中介軸承影響最大，這也是航空發動機中介軸承最容易損壞的原因之一。

不同支承不同心情況下支承4、5處的軸承力3維瀑布圖分別如圖11～13所示。從圖中可見，支承不同心引起了更多的倍頻特征，并出現了“連續”譜特征，表明過多過大的軸承間隙引起系統的運動不穩定，表現出混沌特征。

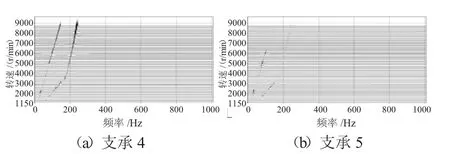
圖11 Case1下的支承軸承力3維瀑布圖

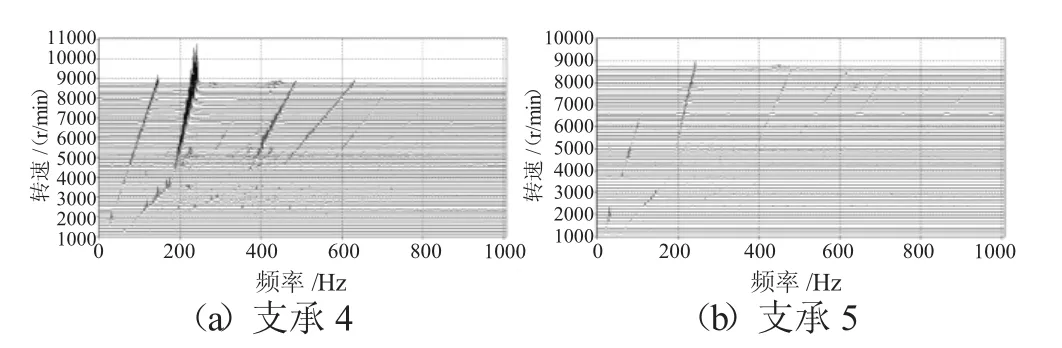
圖12 Case2下的支承軸承力3維瀑布圖

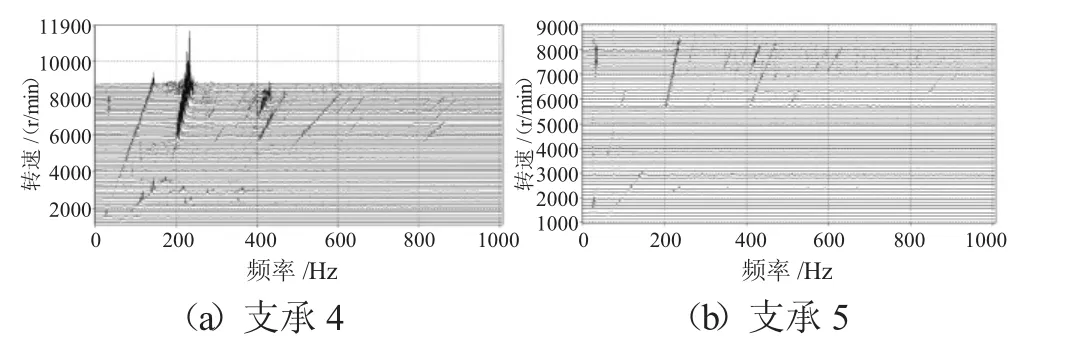
圖13 Case3下的支承軸承力3維瀑布圖

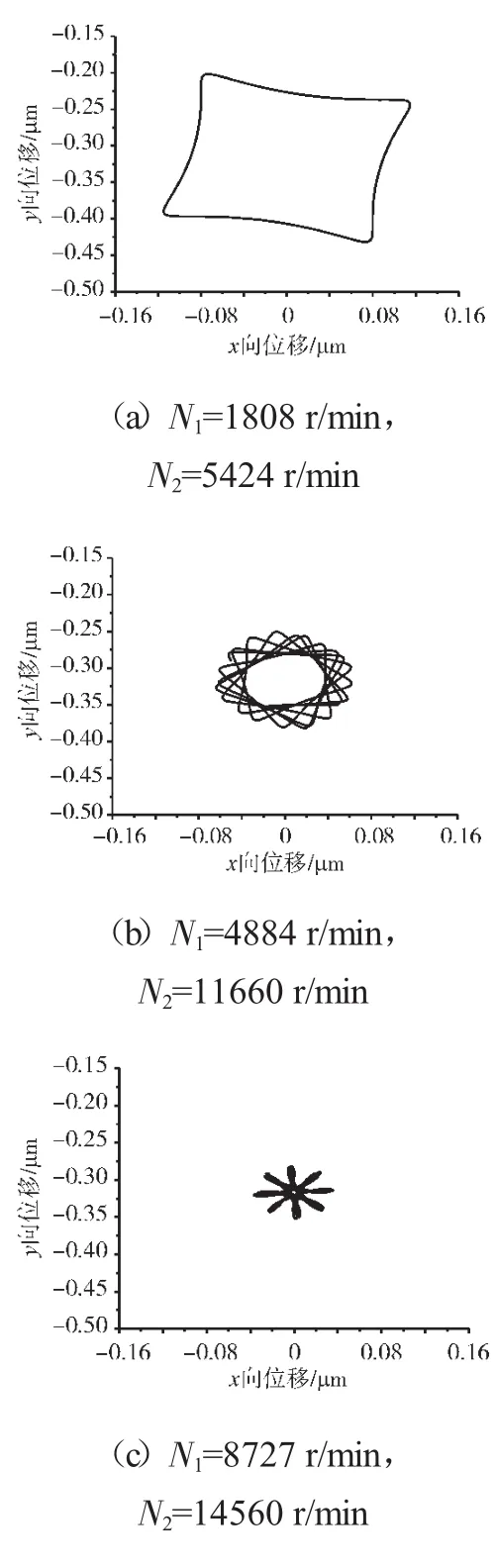
圖14 支承不同心Case1情況下的支承4低壓轉子節點軸心軌跡

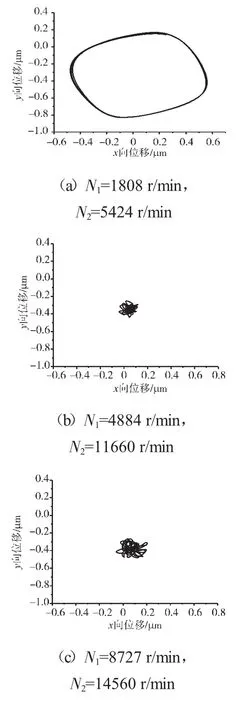
圖15 支承不同心Case2情況下的支承4低壓轉子節點軸心軌跡

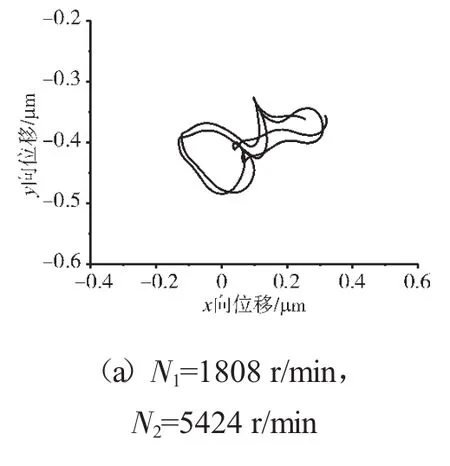
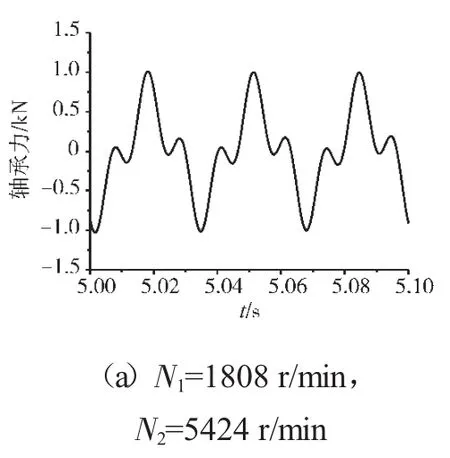
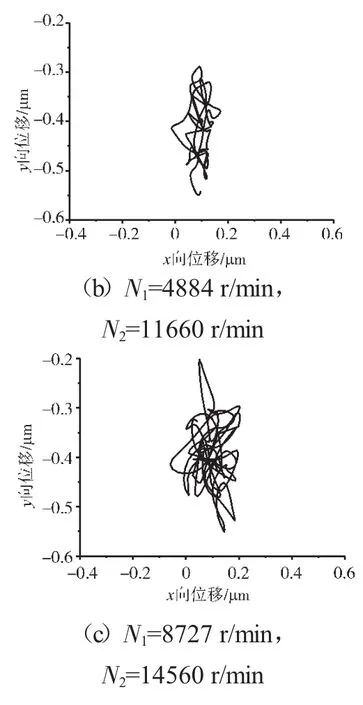
圖16 支承不同心Case3情況下的支承4低壓轉子節點軸心軌跡

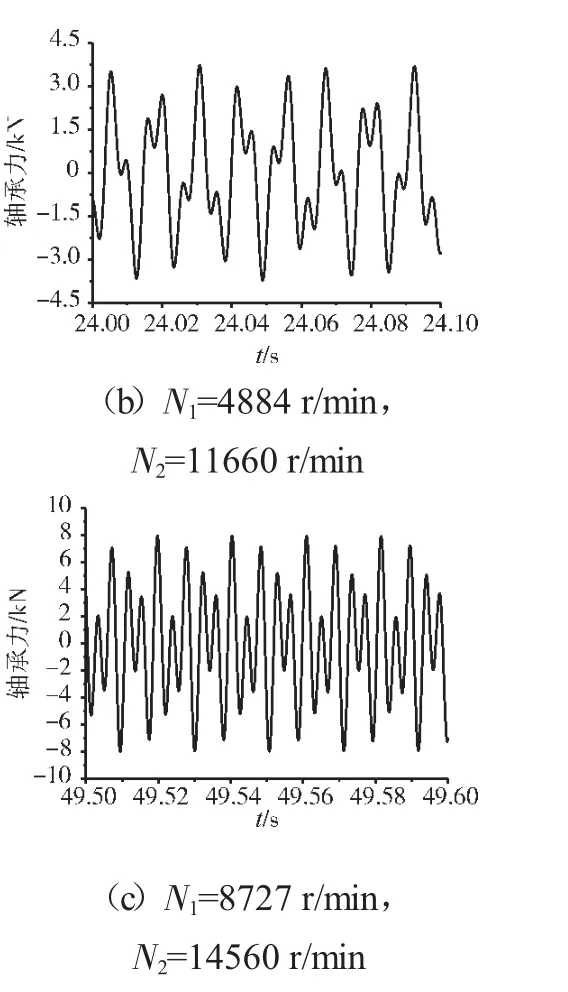
圖17 支承不同心Case1情況下的支承4軸承力時域波形

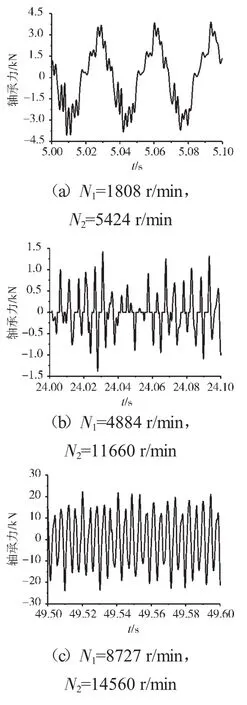
圖18 支承不同心Case2情況下的支承4軸承力時域波形

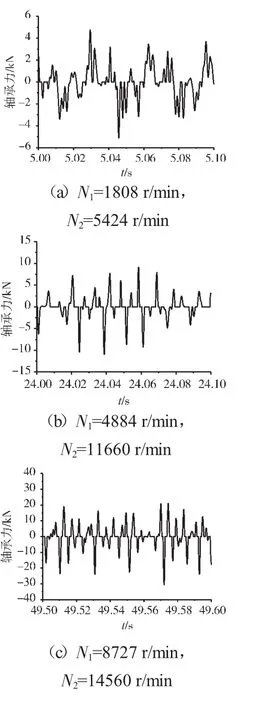
圖19 支承不同心Case3情況下的支承4軸承力時域波形

支承不同心Case1、Case2和Case3下的支承4處低壓轉子節點的軸心軌跡、對應低壓轉子節點的振動加速度時域波形和頻譜分別如圖14～22所示。從圖中可見，在Case1情況下，由于不存在軸承間隙，系統為線性系統，因而軸承力表現為高低壓轉速頻率的組合。這種組合根據高低壓轉速的頻率比值不同而出現不同形狀的很規則的軸心軌跡；在Case2情況下，由于存在軸承間隙，系統表現為非線性特征，軸承力除了高低壓轉速頻率以外還有其他倍頻和“連續”譜成分。這種頻率成分復雜的組合導致軸心軌跡較為紊亂；在Case3情況下，不同心度更大，軸承間隙也更大，系統非線性特征更加強烈，軸承力的“連續”譜成分更加突出，軸心軌跡非常紊亂，系統表現出“混沌”特征。

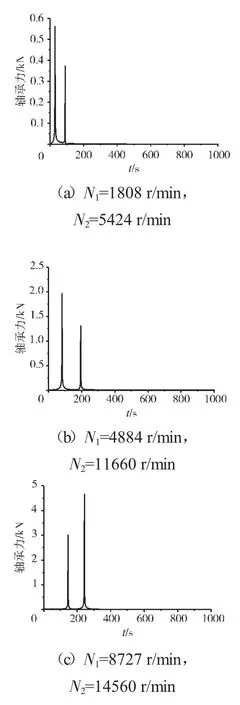
圖20 支承不同心Case1情況下的支承4軸承力頻譜

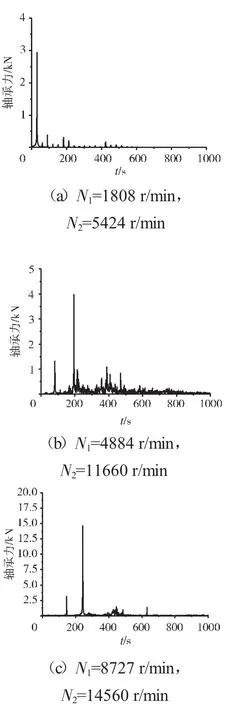
圖21 支承不同心Case2情況下的支承4軸承力頻譜

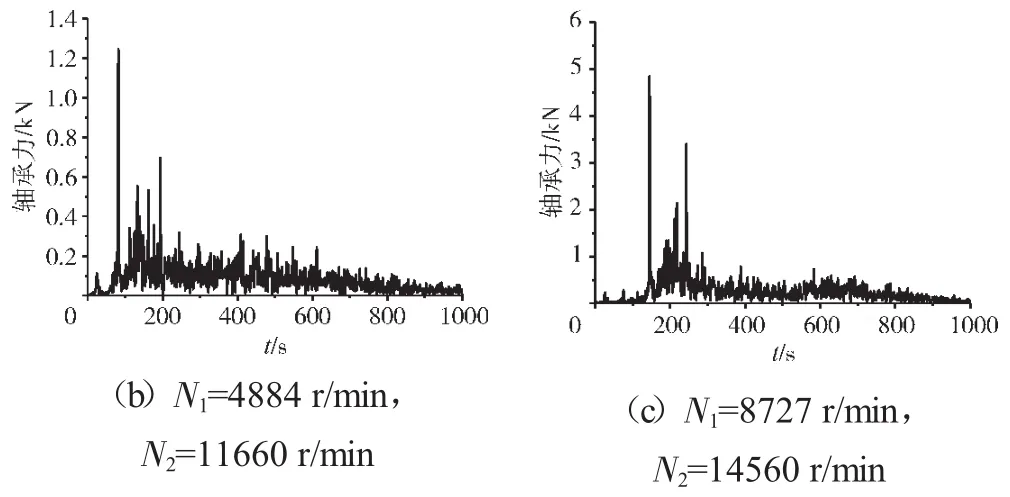
圖22 支承不同心Case3情況下的支承4軸承力頻譜

4 結論

將支承不同心模型與整機振動模型相結合，進行了不同心下的故障仿真計算，并比較了不同的支承不同心度下的支承軸承力、支承處轉子節點加速度、機匣測點處的機匣節點力和機匣測點響應加速度。不同心度需要支承軸承的間隙補償，不同心度越大，要求軸承間隙越大，過大的軸承間隙將引發軸承沖擊，產生很大的軸承力，使轉子運動出現混沌現象，從而影響轉子運動的穩定性。同時，過大的軸承力將引發滾動軸承的疲勞破壞，對于中介軸承尤其如此，這也是實際航空發動機中介軸承容易損壞的重要原因之一。然而，機匣測點響應對不同心的靈敏度并不高，給實際航空發動機支承不同心的診斷帶來困難。