反應擴散模型數值解及生物斑圖中的應用

艾合麥提尼亞孜·艾合麥提江，開依沙爾·熱合曼

(1.和田師范專科學校 數學與信息學院, 新疆 和田 848000;2.新疆大學 數學與系統科學學院, 烏魯木齊 830046)

在研究經典生物動力系統中，很多模型沒有考慮到空間因素而建立差分方程或常微分方程模型來研究生物動力系統生物進化過程。實際上所有動物、植物等生物群體都生活在空間環境中。為了提高研究的準確性，切近現實，在研究某些生物動力系統時，一定要考慮其所在空間和時間中的演化問題[1]。1952年計算機科學之父英國著名數學家 Turing 在論文《形態形成的化學基礎》[2]中用一個反應擴散模型成功地解釋了某些生物群體表面上的圖文，并提出空間斑圖的Turing原理，之后他的研究在物理和化學中得到了發展，但是實驗中一直未能得到證實。1991年我國理論生物學家歐陽頎在實驗中首次發現二維Turing斑圖與Turing分岐[3-4]，從而使理論研究有了實驗上證據。國內外學者也進行了大量空間斑圖的研究。

用反應擴散模型來研究斑圖動力學行為是非常有趣和重要的，便于實施有效的利用和控制以及解釋某些生物反應擴散系統所呈現出來的各種空間斑圖。本文應用幾種常用的反應擴散模型通過計算機模擬手段來研究各種斑圖結構。

1 生物斑圖動力學

生物斑圖(pattern)是在空間或時間上具有某種規律性的非均勻宏觀結構，在大自然經常遇到。動物身上的斑圖(如斑馬、魚、蛇等)都是生物斑圖。生物斑圖在動力學中得到廣泛研究。動物斑圖結構通常是群體之間局部相互作用和擴散形成的，利用反應擴散方程來討論生物群體的空間結構使得我們能有效解釋某些斑圖現象。

2 反應擴散模型

自然界經常看到生物斑圖，如魚外表面的花紋以及斑馬身上的斑紋等，如圖1所示。

為什么會出現這些豐富多彩的紋理形態呢？為了解決這個問題，Turing[2]提出了反應擴散模型，并用一組反應擴散方程闡釋，從而有了生物形態發生的化學理論基礎。模型中的兩種化學反應物質(活化因子和抑制因子)是相互作用的并且獨自擴散的，模型表明了這些分子自發地形成穩定的周期性，被稱作Turing模型。當反應-擴散模型形成Turing模型時，活化因子(activator)及抑制因子(inhibitor)顯示出穩定分布。一般擴散是指濃度和溫度等達到均勻分布的現象。但是，反應擴散系統的穩定狀態在某種條件下將失去均勻化，并自發形成非均勻化現象，體現出了不同的模樣，并且還能說明擴散組織細胞間用化學物質的相互反應來形成形態的現象。

圖1 自然界生物斑圖形態

3 反應擴散模型穩定性分析

下面對雙變量反應擴散系統為例進行線性穩定性分析。雙變量化學反應擴散方程的一般形式為：

(1)

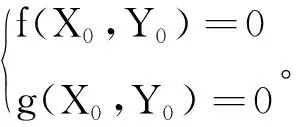
令X=X0+x,Y=Y0+y,代入方程經泰勒級數展開，去掉高階項可得線性微擾方程

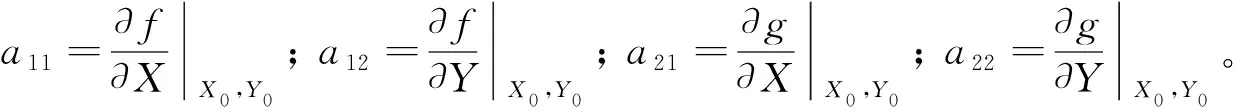
代入微擾方程(2)，可得特征方程：

解特征方程，可得色散關系：

其中：

trk=a11+a22-k2(Dx+Dy)=

tr0-k2(Dx+Dy)

(6)

Δκ=a11a22-a21a12-k2(a11Dx+a22Dy)+

k4DxDy=?Δ0-k2(a11Dx+a22Dy)+k4DxDy

(7)

解得

當λk的實部都小于0時，微擾量衰變為0，而系統穩定。有一個λk>0時，微擾變量不斷增加，系統的均勻定態解(X0,Y0)失穩。設λk是μ的函數：λK=λk(μ)，臨界點μc，λk(μc)=0, ?λk/?μ≠0，則μ=μc是系統的一個動力學分岔(支)點。

4 反應擴散系統中的分支問題

生物反應擴散系統所呈現的各種空間斑圖的根本原因是非線性分支作用破壞了時間和空間的對稱性。這種方程常依賴于各種參數(溫度、催化率和擴散率)。當這些參數發生變化時，方程的解的數目和穩定性都可能發生突然的變化。因此，分支分析是理解動力學的關鍵。

系統的不動點從穩定焦點向不穩定焦點的轉換時出現Hopf分支，對應非平衡相變，是指系統從空間均勻定態到對時間的周期振蕩態，對應時間平移對稱性破缺。當系統在臨界點，即trk=0時，如果Δk>0，則系統出現Hopf分支，文獻[7]中詳細地介紹了Hopf分支。

文獻[8]給出Turing分支發生的必要條件，并且給出系統分支區域，見圖2。

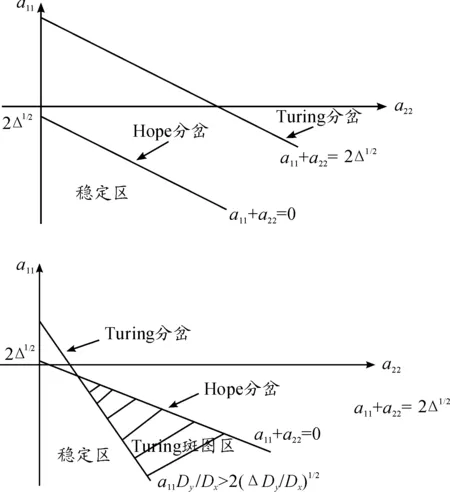
圖2 系統分支區域

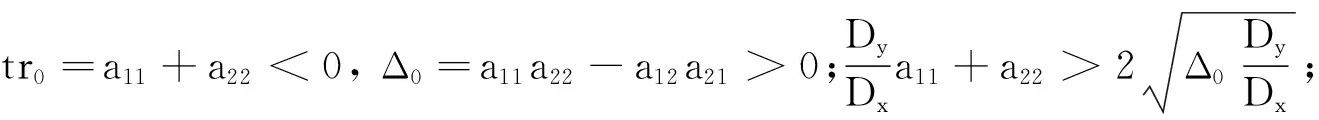
5 利用Matlab數值模擬Gray-Scott模型

化學有一個反應擴散系統，稱之為Gray-Scott模型[9]，該模型實驗證明參考理論分析[10]可以參考斑圖實驗[11-13]，下面討論模型不同時間段的數值模擬。

(9)

取初始條件為：

當1≤x,y≤1.5時，

u(x,y,0)=1-2v(x,y,0)

參數取值為：D1=8×10-5，D2=4×10-5，γ=0.024,κ=0.06[10]。由數值微分公式得到下面的離散形式：

(10)

利用Matlab得到的在不同時間段離散結果的圖像如圖3所示。

6利用Matlab數值模Schnackenberg模型

Schnackenberg 模型[12]最早是在研究三分子自催化反應時提出的。量綱為一方程為：

參數取值為[13]：γ=800,a=0.250, b=0.1, d=20。

初始條件如下:

u0=cos(2πx)cos(2πy)

v0=cos(2πx)cos(2πy)

(12)

利用Matlab得到的不同區間的離散結果圖像如圖4所示。

我們發現模擬得到的圖像與自然界某些生物斑圖基本相似，如圖5所示。

7 利用Excel數值模擬Gray-Scott模型

對于Gray-Scott模型，同樣利用顯式差分格式Gray-Scott模型離散形式(10)，有關參數取值如下：dt=0.01, dx=0.05,γ=3，κ=2，D1=0.03,D2=0.033。

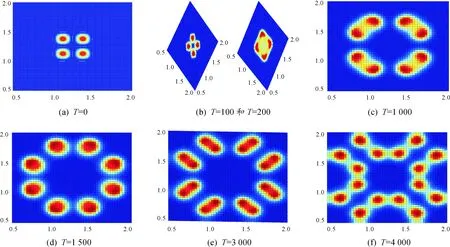
圖3 Gray-Scott模型的時間演化

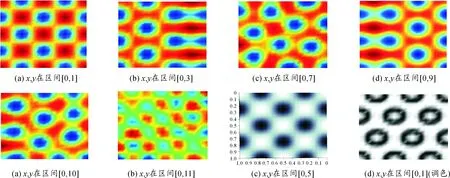
圖4 Schnackenberg 模型的空間演化

圖5 實驗結果圖與生物圖比較

巧妙應用Microsoft Excel的重新計算和迭代計算功能，將通過1 400次迭代計算得到的數據插入曲面圖表得到圖6。

圖6 Gray-Scott模型Excel離散圖

8 結果分析

本文以常用的反應擴散模型Gray-Scott模型和Schnackenberg 模型為例，用差分方法，運用Excel和Matlab工具對具有不同的初始條件、不同的空間尺度、不同的時間段的兩種模型進行計算機數值模擬，從而得到了各種各樣相似于生物斑圖結構，通過數值模擬的結果我們發現：不同的區間和時間對斑圖形成與形狀有一定的影響，但對一定空間標準的群體而言，充分長的周期內生物群體在空間中能表現出一定的空間有序斑圖結構。