基于Matlab/Simulink的發動機扭振實時模型的建立

石曉輝，汪楊凡，李文禮,，王晶晶，張向奎，何 洋

(1.重慶理工大學 汽車零部件先進制造技術教育部重點實驗室， 重慶 400054；2.重慶工程職業技術學院， 重慶 402260；3.重慶青山工業責任有限公司， 重慶 402761)

發動機高瞬態扭振模擬技術是汽車傳動系動態模擬試驗的關鍵技術之一[1-3]。發動機具有無限多階的振動模態，軸系會按其受到的激振載荷的頻率進行強迫振動。發動機扭振模擬技術可以再現實車扭振激勵信號，該信號可以作為傳動系NVH臺架與變速器硬件在環試驗等試驗的激勵源，能比較真實地復現實車運行狀態，便于研究被測部件運行特性受到扭振激勵的影響。若要在室內臺架上模擬發動機扭振激勵對傳動系統被測件的影響，則需要一個高動態響應的發動機實時控制模型作為激勵源。因此，如何建立一個高動態響應的發動機高瞬態扭振實時控制模型是發動機高瞬態扭振模擬技術的關鍵與難點[4-6]。發動機扭振模擬技術是一個集機械、電子、控制等多學科為一體的復雜學科，國內外眾多學者對其進行了研究，為發動機扭振模擬技術的發展作出了貢獻[7-8]。

發動機扭振模擬技術在很多文獻中都有論述。文獻[9-10]分別提及到了黑箱模型和基于物理結構的模型。然而這些模型對發動機的開發參數依賴過大，且在模擬過程中很難滿足高動態控制響應的要求，因此不適用于臺架模擬試驗。文獻[5]采用了高頻液壓控制器與自使用閉環控制，可以得到比較真實的扭振曲線，但是該種方案下液壓控制系統維護比較困難。文獻[6]建立了基于交流異步電機模擬汽車發動機的非線性系統模型，并分析對比了開環轉矩補償法和帶有開環轉矩前饋的閉環轉速控制法之間的優劣。

筆者以某款發動機為參考，利用Matlab/Simulink建立了一套可以應用于汽車試驗臺架的發動機高瞬態扭振實時控制模型。

1 發動機高瞬態扭振實時控制模型

激振載荷是引起系統軸系振動的能量來源，對于發動機軸系來說主要的激勵載荷分為3種，即發動機運動部件的慣性載荷引起的激振力矩、發動機工作時由于汽缸內氣體比力變化而引起的激振力矩、接受功率的部件吸收功率不均勻而產生的激振力矩。其中前兩種激振力矩為引起發動機軸系扭振的主要因素，第3種激振力矩對車用發動機的影響很小，這里不對其進行討論。因此，總的發動機扭矩可以表示為：

Ten=TI+TC

(1)

式中： Ten為總的發動機扭矩(N·m)； TI為往復慣量引起的激勵扭矩(N·m); TC為燃燒壓力引起的激勵扭矩(N·m)。

2 發動機慣量扭矩模型

發動機曲柄連桿機構的慣性力分為離心慣性力和往復慣性力。離心慣性力作用方向始終通過曲軸回轉中心，故它對曲柄的作用力為0，不會引起扭轉振動。而其往復慣性力通過連桿作用在曲柄銷上產生周期性變化的切向力矩，該力矩即為引起軸系扭振的動力。單缸往復運動慣性力模型如圖1所示。

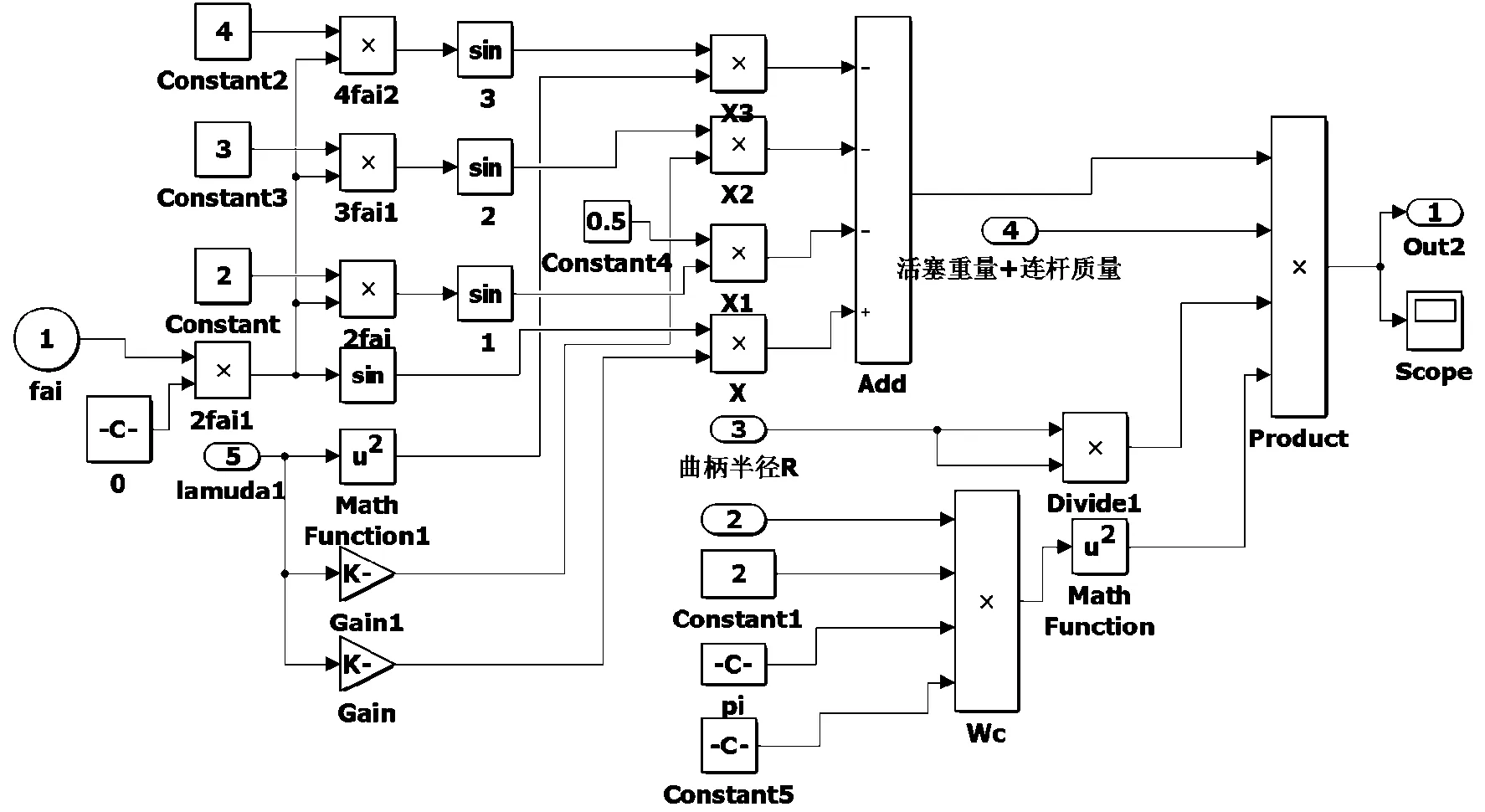
圖1 單缸往復運動慣性力產生的激振力

往復慣性力為：

pj=-mja=-mjrω2(cosα+λcos2α)

(2)

上述往復慣性力通過連桿軸頸對曲軸形成的力矩為：

將式(1)代入式(2)可得：

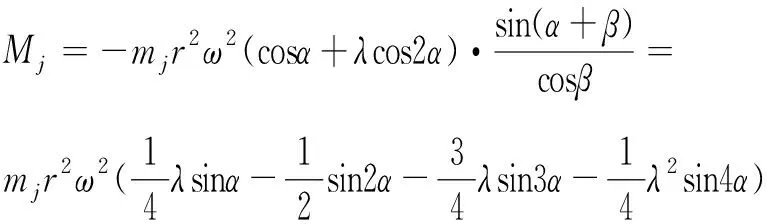
(4)

式中：mj為單個汽缸往復運動質量(g·s/cm)； r為曲柄回轉半徑(cm)； α為曲軸轉角(rad)； λ為曲柄連桿機構常數，λ=r/L；L為連桿長度(cm)。

激振力矩Mj雖然可以分解成很多的簡諧力矩,但是在計算到第4階時已經可以滿足實際應用中的精度要求。

3 發動機燃燒扭矩模型

3.1 基本微分方程

聯立能量守恒方程、質量守恒方程、理想氣體方程3個方程構成描述發動機缸內實際過程的基本微分方程組[2-3]：

使用歐拉法對方程組(5)進行數值求解,能夠得到缸內溫度T、缸內壓力P、工質質量m等熱力狀態參數隨著曲軸轉角的變化規律。

3.2 各熱力過程數學模型的建立

發動機的工作過程可以簡化分為壓縮、燃燒、膨脹、換氣等4個階段，本文研究的模型即是通過這4個過程來對發動機的壓力變化進行研究。

3.2.1 壓縮階段

從進氣門關閉到混合氣開始燃燒，不存在燃料燃燒放熱過程，僅僅是對一定質量的氣體不斷壓縮，故存在以下關系：

質量守恒簡化為：

能量守恒方程簡化為：

壓縮階段模型見圖2。

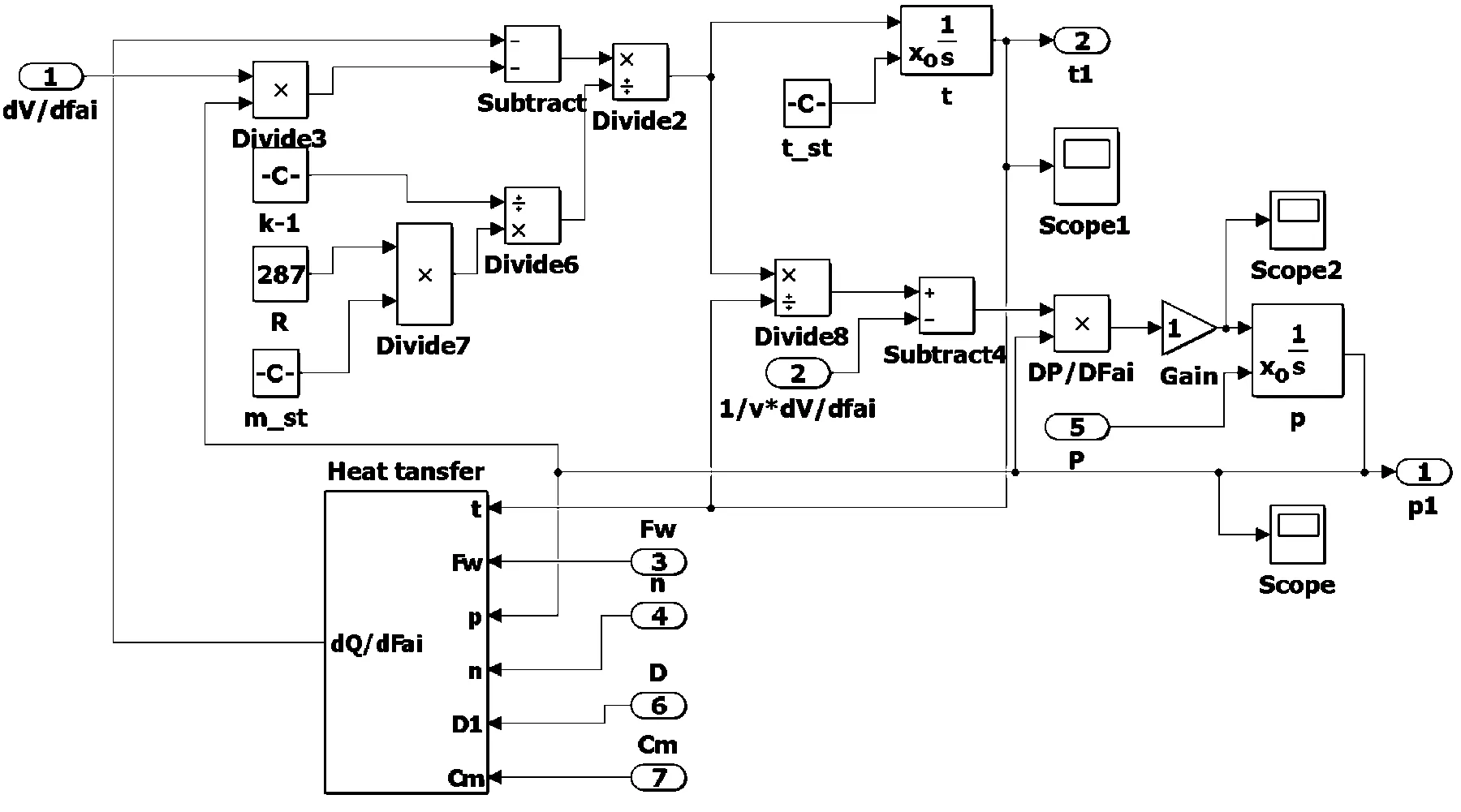
圖2 壓縮階段

3.2.2 燃燒階段

燃燒階段模型見圖3。

3.2.3 膨脹階段

膨脹階段由燃燒終點起至排氣門開啟時刻止。膨脹階段從燃燒結束一直到排氣門打開，與壓縮階段相似。

能量守恒方程簡化如下：

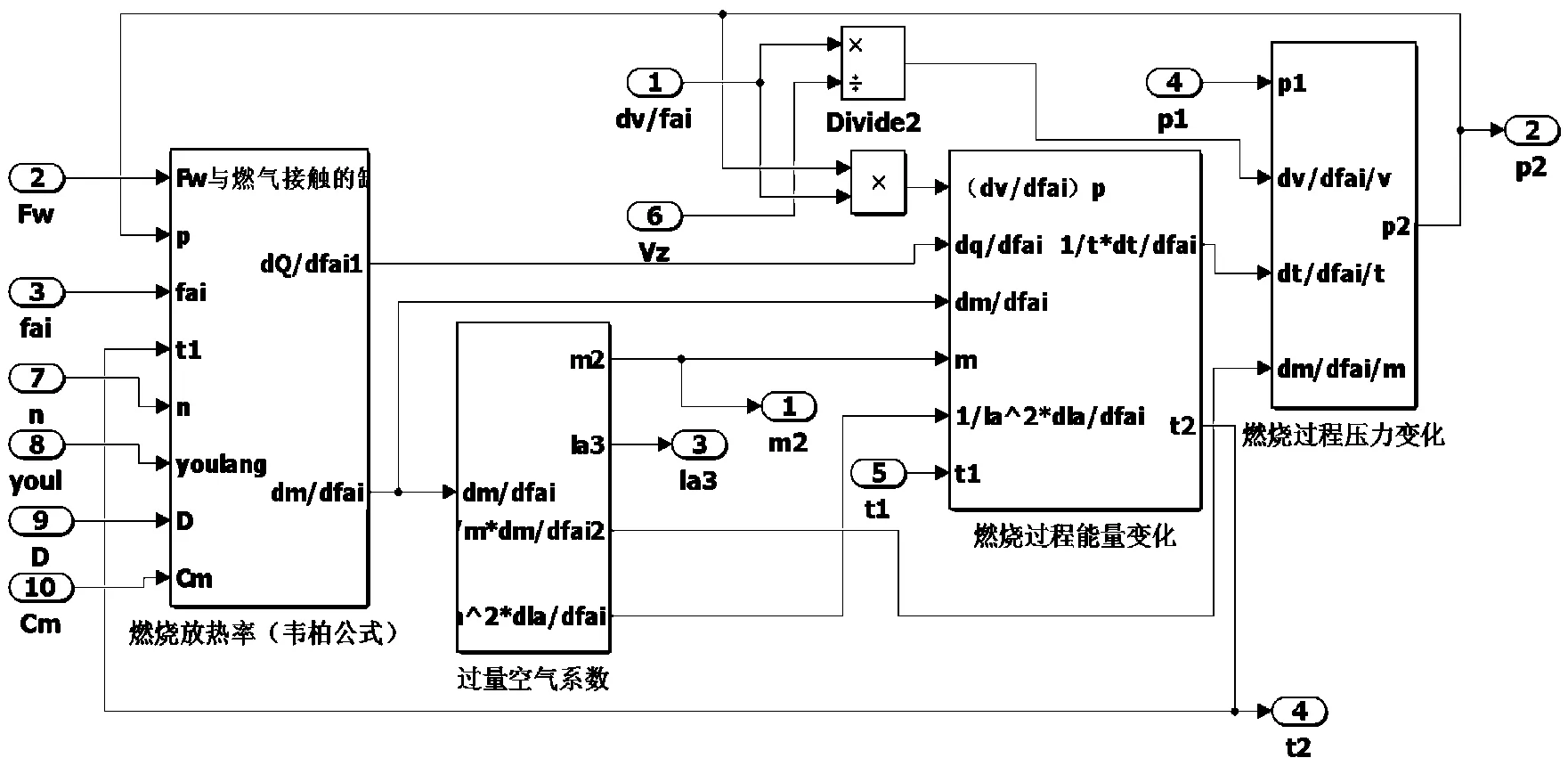
圖3 燃燒階段

3.2.4 純排氣階段

單純排氣階段從排氣門打開開始一直到進氣門打開為止。質量守恒方程簡化如下：

能量守恒方程簡化如下：

(12)

3.2.5 純進氣階段

單純進氣階段從排氣門關閉一直持續到進氣門關閉。

質量守恒方程簡化為：

能量守恒方程簡化為：

3.2.6 進排氣疊開階段

質量守恒方程：

能量守恒方程：

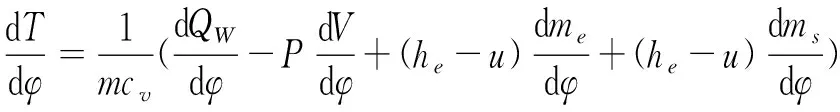
(16)

3.3 邊界條件的確定

發動機工作過程中有眾多的邊界條件有待通過計算獲得，例如過量空氣系數、汽缸容積等。

3.3.1 過量空氣系數

瞬時過量空氣系數αφ為實際空氣質量mL和燃燒理論上所需的空氣量mB的比值：

式中：m為汽缸內工質總質量；mL為汽缸內的實際空氣質量；mB為某瞬間前汽缸內已燃燒的燃油質量；L0為理論空氣量(L0=14.3 kg)。

瞬時過量空氣系數隨曲軸轉角的變化率為：

3.3.2 瞬時絕熱指數kφ和比熱C

瞬時絕熱指數kφ利用串山公式計算:

kφ=1.437 3-1.318×10-4·T+

3.12×10-8·T2-4.8×10-2/αφ

當R、k求得之后，可以利用熱力學公式計算比熱(kJ/(kmol·K))：

3.3.3 汽缸工作容積

瞬時汽缸工作容積為

汽缸容積的變化率為

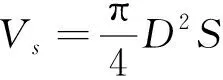
瞬時汽缸容積模型見圖4。

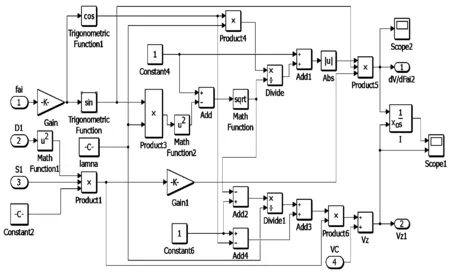
圖4 瞬時汽缸容積

3.3.4 內能u和焓h

h=u+RT

u=Cv·T

h=Cp·T

(22)

3.3.5 汽缸周壁傳熱

氣體對汽缸周壁的放熱率為

其中FW=4V/D為汽缸內壁平均溫度。

根據胡希尼(G.Woschni)在1965年提出的公式可得：

KW=265D-0.214(Cmp)0.786T-0.525

(24)

式中Cm為活塞平均速度(Cm=S·n/30)。

3.3.6 燃燒過程的放熱規律

發動機的燃燒過程極其復雜,燃燒模型建立的好壞直接影響最終的仿真結果。通用的Vibe燃燒模型由于具有控制參數少、結構簡單等優點，在發動機模型計算研究中被廣泛應用。

Vibe公式為：

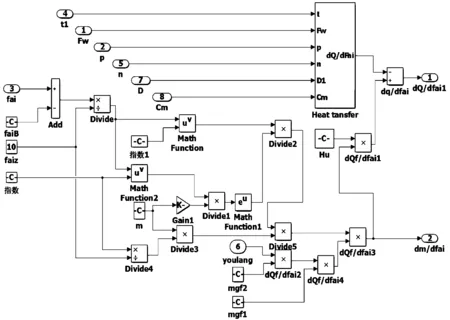
圖5 Vibe公式

3.3.7 單個汽缸激振力矩

單個汽缸內氣體工作壓力對曲軸產生的激振力矩為

式中：Pg為汽缸內工質壓力(kg/cm)；D為汽缸直徑(cm)。

單個汽缸內氣體工作壓力對曲軸產生的激振力矩模型見圖6。

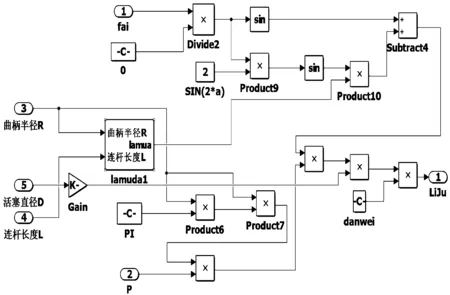
圖6 單個汽缸內氣體工作壓力對曲軸產生的激振力矩

4 模型驗證

本文研究的試驗數據為模型仿真信號與商業軟件AMESim仿真信號的跟蹤對比。

發動機扭振模擬試驗以某四缸四沖程汽油機為模擬對象，該機型的相關參數如表1所示。圖7為汽缸壓力產生的激振力矩，圖8為模擬信號單個汽缸產生的慣性力矩。通過缸平移法按照點火順序依次將四缸的單個汽缸壓力產生的激振力矩與單個汽缸產生的慣性力矩相疊加，得到最終的發動機扭振模擬信號。

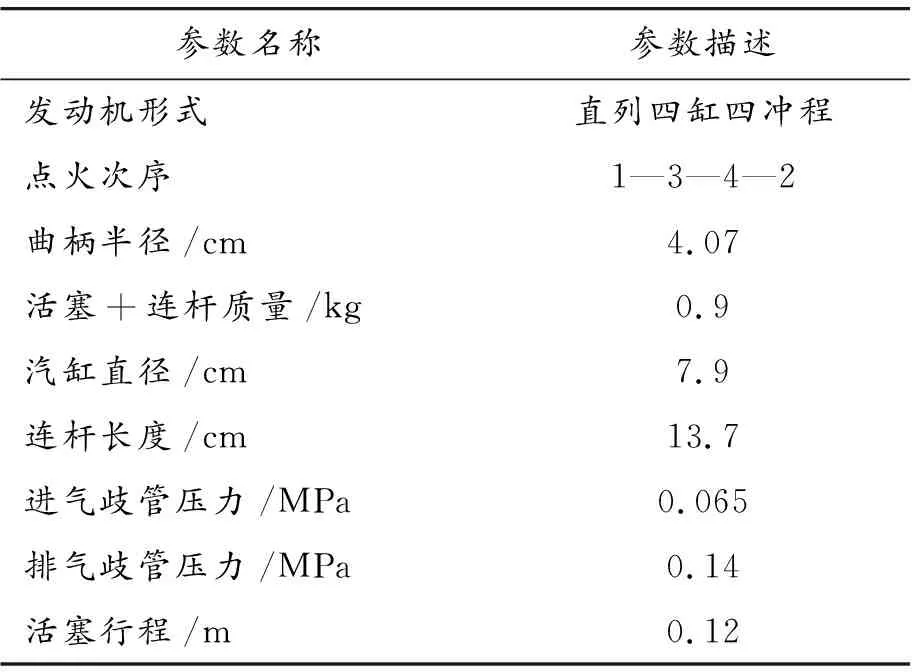
表1 某款直列四缸四沖程汽油發動機參數

在圖9～12中，Ten為模擬參考信號，T1為實測扭振信號，均進行了平滑濾波處理。本文從眾多數據中挑選了發動機2 000 r/min油門開度分別為50和70與3 000 N/min油門開度分別為70和100四個工況。

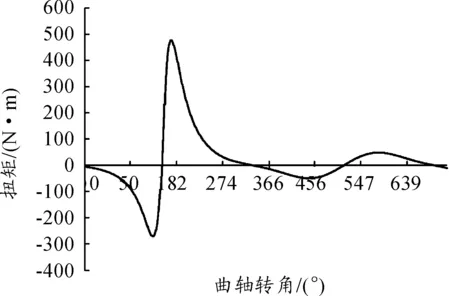
圖7 汽缸壓力產生的激振力矩

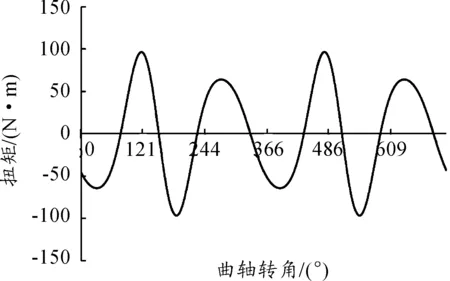
圖8 單個汽缸產生的慣性力矩曲線

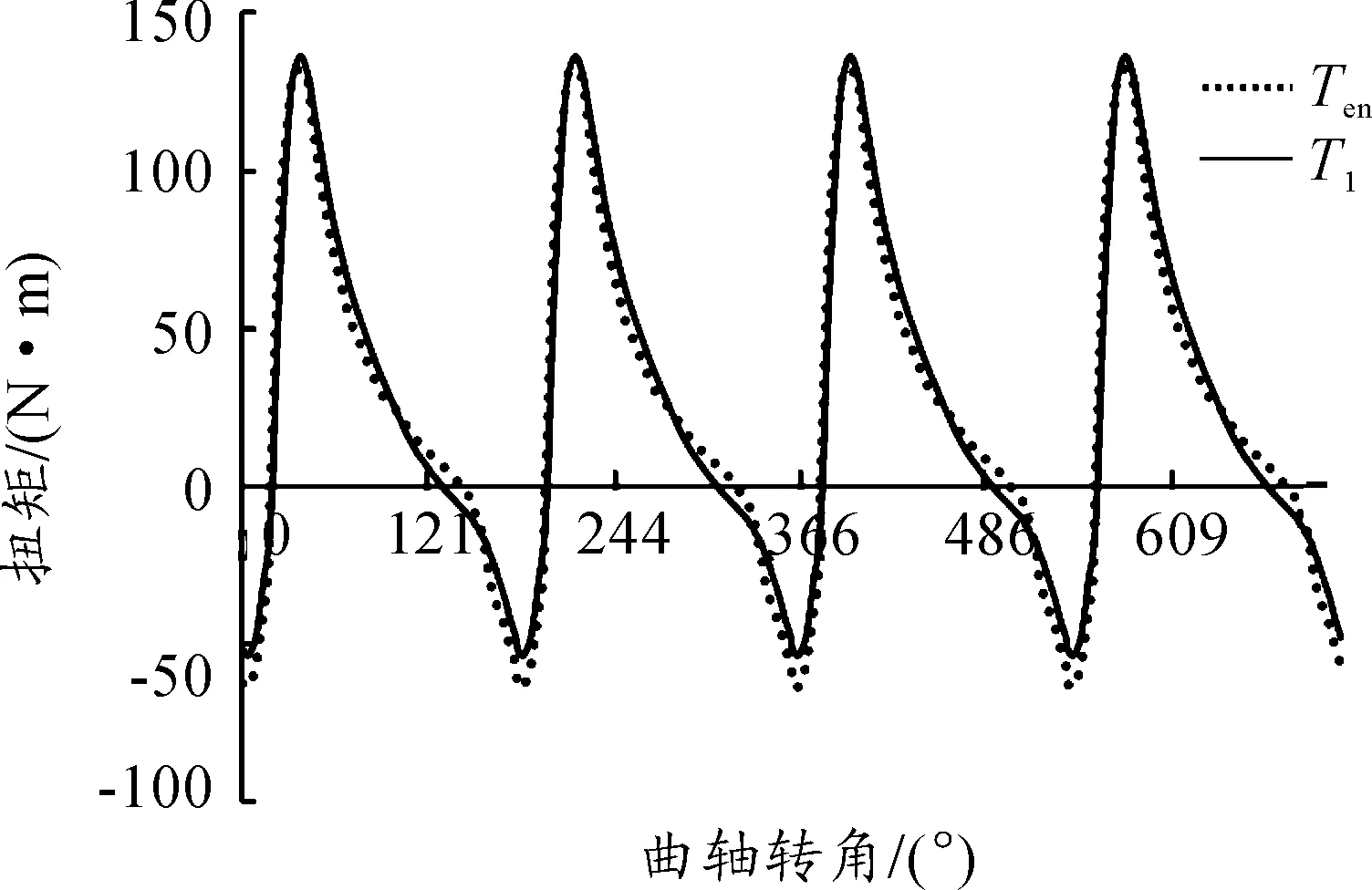
圖9 發動機轉速為2 000 r/min、油門開度為50%時的扭振曲線對比

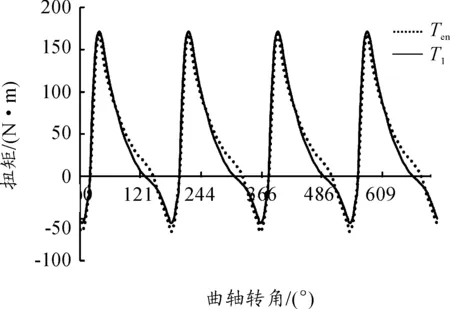
圖10 發動機轉速為2 000 r/min、油門開度為70%時的扭振曲線對比

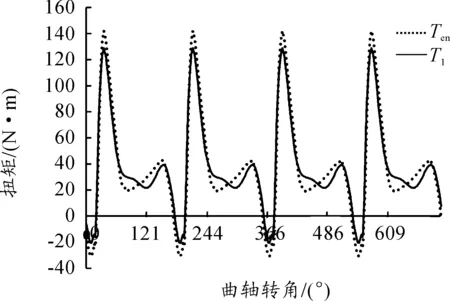
圖11 發動機轉速為3 000 r/min、油門開度為70%時的扭振曲線對比

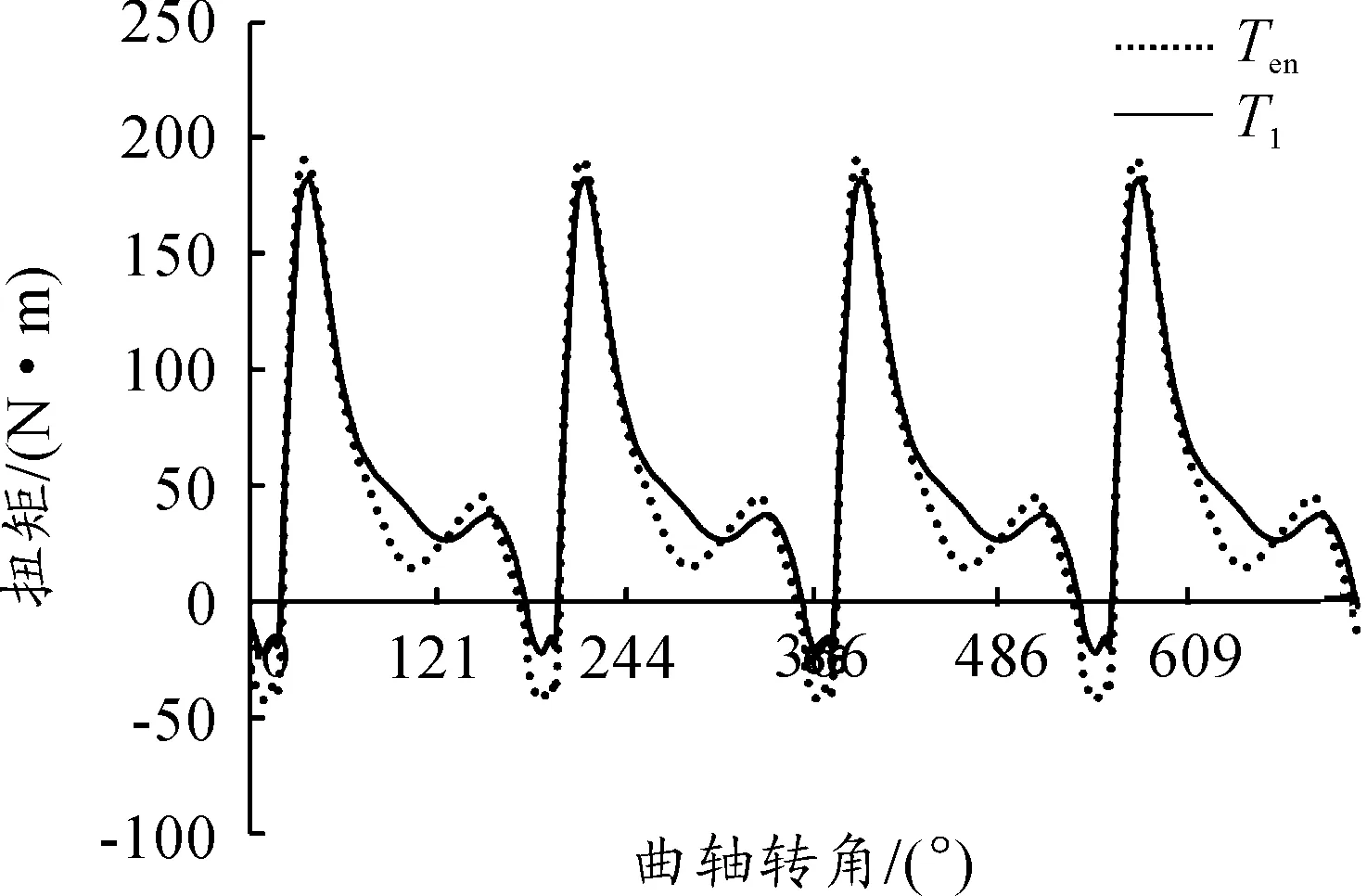
圖12 發動機轉速為3 000 r/min、油門開度為100%時的扭振曲線對比

表2 發動機轉速為2 000 r/min、油門開度為70%時Simulink模擬和商業軟件AMESim仿真數據分析 N·m

表3 發動機轉速為3 000 r/min、油門開度為70%時Simulink模擬和商業軟件AMESim仿真數據分析 N·m

與商業軟件AMESim仿真信號相比，模擬信號誤差較低，精度較高，能有效地反映實測信號的扭振特性，證明在所提供的參數較少的情況下，該發動機高瞬態扭振模型能較為精確地模擬發動機扭轉振動特性。

5 結束語

本文以某款四缸四沖程汽油發動機為參考機型，利用Matlab/Simulink建立了一套可以應用于汽車試驗臺架的發動機高瞬態扭振實時控制模型。仿真與試驗對比結果表明:該仿真模型在所提供的參數較少的情況下，能較為精確地模擬發動機扭轉振動特性。

本研究所建立的發動機扭振實時控制模型計算量較小，運行速度快，可以滿足發動機模擬高動態實時控制的要求，輸出信號能為傳動系NVH臺架與變速器硬件在環試驗等試驗提供有效激勵源。該模型為試驗臺架動態測試提供了理論基礎，對發動機扭振模擬技術的研究有著重要意義。