一種減小相控陣天線球面近場(chǎng)測(cè)量截?cái)嗾`差的方法

于丁 張虎勇 陳佩玉 楊林 傅德民

(西安電子科技大學(xué) 天線與微波技術(shù)重點(diǎn)實(shí)驗(yàn)室,西安 710071)

引 言

根據(jù)球面近場(chǎng)天線測(cè)量的模式展開理論,天線在無源區(qū)域的輻射場(chǎng)可以表示為球面波模式的加權(quán)和[1]. 無論是在天線的近場(chǎng)輻射區(qū)還是遠(yuǎn)場(chǎng)輻射區(qū),球面波模式的系數(shù)不會(huì)發(fā)生改變,因此球面波模式系數(shù)的求解就成了球面近場(chǎng)測(cè)量的核心問題,它是近場(chǎng)和遠(yuǎn)場(chǎng)之間的一座橋梁. 通常情況下,球面波模式系數(shù)是利用各模式之間的正交性,在包圍待測(cè)天線的采樣球面上進(jìn)行積分來獲得. 理論上,如果要得到高精度的計(jì)算結(jié)果,需要知道整個(gè)包圍待測(cè)天線采樣面上的完整數(shù)據(jù)[2]. 在實(shí)際測(cè)量中,采樣面上的部分區(qū)域的近場(chǎng)數(shù)據(jù)往往不能獲得,在近遠(yuǎn)場(chǎng)變換時(shí),一般將未采樣區(qū)域的近場(chǎng)置為零. 因此,在掃描面邊界就會(huì)形成突然的不連續(xù)性,這將會(huì)引入截?cái)嗾`差. 尤其對(duì)于相控陣天線,在波束掃描情況下,當(dāng)最大輻射方向和掃描面邊界相距較近時(shí),往往會(huì)引起較大的截?cái)嗾`差.

關(guān)于這種截?cái)嗾`差減小的方法在一些文獻(xiàn)中有提到[3],例如通過建立一個(gè)線性系統(tǒng)的匹配技術(shù)對(duì)不完整的測(cè)量數(shù)據(jù)來預(yù)估球面波模式系數(shù)可以減小截?cái)嗾`差[4],通過這種方法也衍生出了許多近場(chǎng)數(shù)據(jù)的重構(gòu)技術(shù). 目前減小球面近場(chǎng)測(cè)量中的截?cái)嗾`差主要有兩種方法:一種是基于模式展開和模式濾波的迭代算法[5-6],利用天線輻射場(chǎng)球面波模式個(gè)數(shù)是嚴(yán)格由包圍待測(cè)天線最小球的半徑?jīng)Q定的,文獻(xiàn)[7]在高整合車載天線測(cè)量時(shí)用到了這種方法. 另一種方法是基于等效電流(equivalent current, EQC)展開的[8],這種方法把EQC看作最小能量算子,在采樣區(qū)域和截?cái)鄥^(qū)域之間形成一個(gè)平滑的過度. 還有將模式濾波方法用在減小平面近場(chǎng)測(cè)量中的環(huán)境誤差[9],這種方法是將平面近場(chǎng)測(cè)量求得的方向圖經(jīng)過坐標(biāo)平移后用球面波模式展開后再進(jìn)行模式濾波,和球面近場(chǎng)測(cè)量的模式濾波本質(zhì)上是一樣的. 本文提出一種通過余弦窗函數(shù)對(duì)近場(chǎng)數(shù)據(jù)加權(quán)來減小截?cái)嗾`差的方法,根據(jù)采樣內(nèi)插原理對(duì)近場(chǎng)數(shù)據(jù)進(jìn)行加權(quán),使近場(chǎng)數(shù)據(jù)在采樣區(qū)域和未采樣區(qū)域的邊界處平滑過渡,從而使截?cái)嗾`差減小.

1 基于模式展開的球面近遠(yuǎn)場(chǎng)變換

基于模式展開的球面近遠(yuǎn)場(chǎng)變換的基本思路是天線在無源區(qū)域的輻射場(chǎng)用球面波模式的加權(quán)和來表示,無論是近場(chǎng)還是無窮遠(yuǎn)處球面波模式的系數(shù)不變,因此在近場(chǎng)區(qū)域求得球面波模式系數(shù)后通過對(duì)特殊函數(shù)的大宗量近似就可以求得遠(yuǎn)區(qū)場(chǎng)的性質(zhì)[1].

設(shè)一個(gè)線極化探頭在包圍待測(cè)天線近場(chǎng)區(qū)域的球面上分別在θ方向和φ方向進(jìn)行數(shù)據(jù)采集,在理想情況下探頭的輸出等于或正比于輻射場(chǎng)電場(chǎng)的強(qiáng)度,則在該球面上輻射場(chǎng)電場(chǎng)的切向場(chǎng)可表示為

(1)

由于掃描面處于無源區(qū)域,因此探頭采集的場(chǎng)還可表示為

(2)

式中,M和N是標(biāo)量亥姆霍茲方程的解生成的矢量函數(shù),且滿足矢量亥姆霍茲方程,它們的表達(dá)式為

(3)

(4)

(5)

球面波模式系數(shù)amn和bmn可以利用球面波模式的正交性分別乘其共軛在掃描面上積分求得:

(6)

(7)

在遠(yuǎn)區(qū)場(chǎng)可以對(duì)球漢克爾函數(shù)及其導(dǎo)數(shù)進(jìn)行大宗量近似來處理,其近似表達(dá)式為:

(8)

(9)

式(8)和式(9)中都包含了球面波因子e-jkr/(kr),因去除球面波因子后剩下的部分只與θ和φ有關(guān),據(jù)此可以求得遠(yuǎn)場(chǎng)方向圖函數(shù)的各分量為:

(10)

(11)

則遠(yuǎn)場(chǎng)方向圖函數(shù)為

(12)

2 余弦窗函數(shù)

在實(shí)際測(cè)量中,由于近場(chǎng)數(shù)據(jù)采集不完整,而在球面上通過積分求解模系數(shù)時(shí)只能把未采集到的數(shù)據(jù)設(shè)為零,這就意味著求解積分時(shí)待測(cè)天線在未采樣區(qū)域的輻射場(chǎng)是不正確的. 這種數(shù)據(jù)在采集區(qū)域到未采集區(qū)域的突然不連續(xù)性形成了截?cái)嗾`差. 研究發(fā)現(xiàn),在球面近場(chǎng)測(cè)量中對(duì)包含在截?cái)鄥^(qū)域的近場(chǎng)數(shù)據(jù)進(jìn)行加窗處理可以有效地減小截?cái)嗾`差,讓測(cè)量精度達(dá)到預(yù)期要求. 本節(jié)從數(shù)字信號(hào)處理的思路出發(fā),將窗函數(shù)應(yīng)用在相控陣天線球面近場(chǎng)測(cè)量中來減小截?cái)嗾`差.

由采樣定理可知,對(duì)于一個(gè)有限帶寬的模擬信號(hào)xa(t),如果采樣信號(hào)的角頻率大于或等于該信號(hào)角頻率的兩倍,則該信號(hào)可以由抽樣值唯一表示. 設(shè)采樣信號(hào)為pδ(t),則采樣后的信號(hào)可以表示為

(13)

對(duì)式(13)兩邊取傅里葉變換得

(14)

(15)

該式即為內(nèi)插函數(shù),它表明了模擬信號(hào)如何通過采樣信號(hào)恢復(fù),即原模擬信號(hào)等于采樣值乘以對(duì)應(yīng)的插值函數(shù)的和.

內(nèi)插函數(shù)可以看作是原采樣信號(hào)的加權(quán)函數(shù),即對(duì)各個(gè)采樣點(diǎn)加了權(quán)值,加權(quán)函數(shù)也稱為窗函數(shù).在球面近場(chǎng)測(cè)量中,對(duì)包含在截?cái)鄥^(qū)域的近場(chǎng)數(shù)據(jù)加窗時(shí),應(yīng)同時(shí)考慮對(duì)其幅度和相位加窗.

窗函數(shù)的類型有很多,這里重點(diǎn)對(duì)余弦窗函數(shù)做介紹．

余弦窗函數(shù)的幅度分布和相位分布如圖1所示,x%是單側(cè)加窗范圍占整個(gè)采樣范圍的百分比,dmp是最大相位延遲. 設(shè)一個(gè)方向采樣總點(diǎn)數(shù)為N,采樣間隔為dθ,因此采樣長度為W=(N-1)dθ,設(shè)

(a) 幅度分布(a) Magnitude of T(n)

(b) 相位分布(b) Phase of T(n)圖1 余弦窗函數(shù)的幅度和相位分布Fig.1 The magnitude and phase distribution of the cosine window function

余弦窗函數(shù)的表達(dá)式為

T(n)=A(n)ejP(n).

(16)

式中,n=1,2,3,…,N;A(n)為幅度;P(n)為相位,它們的表達(dá)式為

(17)

(18)

因?yàn)橛嘞掖昂瘮?shù)是一個(gè)復(fù)數(shù)窗,既包含了幅度,又包含了相位. 而近場(chǎng)數(shù)據(jù)也是復(fù)數(shù),因此要考慮到既對(duì)幅度加窗,也要對(duì)相位加窗. 還應(yīng)該注意的是加窗方式[10],對(duì)于包含在截?cái)鄥^(qū)域的球面采樣數(shù)據(jù)既可以在θ方向加窗,也可以在θ和φ方向同時(shí)加窗. 由于本文中的例子只在θ方向引入了截?cái)嗾`差,為了方便說明窗函數(shù)對(duì)減小截?cái)嗾`差的作用,文中的所有加窗均只在θ方向加窗,如圖2所示.

圖2 一種沿θ方向的加窗方式Fig.2 A method of window weighted along the θ direction

3 計(jì)算機(jī)仿真

本文以半波對(duì)稱振子陣列為天線模型,來驗(yàn)證球面近遠(yuǎn)場(chǎng)變換的正確性. 如圖3所示,半波對(duì)稱振子陣列位于xoy平面上, 且振子單元沿x軸方向

放置. 設(shè)振子在x方向放置的個(gè)數(shù)為M′=13,間距為dx=0.7λ(λ為波長);在y方向放置的個(gè)數(shù)為N′=9,間距為dy=0.7λ,對(duì)稱振子單元的編號(hào)如圖3中所示. 設(shè)陣列單元沿x方向和y方向的波腹電流分布分別為-55 dB副瓣的切比雪夫分布和余弦分布. 該半波對(duì)稱振子陣列的理論近場(chǎng)數(shù)據(jù)可由文獻(xiàn)[11]求得,理論遠(yuǎn)場(chǎng)方向圖可由文獻(xiàn)[12]求得.

圖3 半波對(duì)稱振子陣列模型Fig.3 The half-wavelength dipole array model

3.1 余弦窗函數(shù)的應(yīng)用

設(shè)該陣列天線在近場(chǎng)數(shù)據(jù)的截?cái)嘟菫棣萾=45°,不失一般性,設(shè)天線最大輻射方向?yàn)棣?20°,φ=0°. 在有限掃描面和整個(gè)采樣球面情況下,球面近遠(yuǎn)場(chǎng)變換所得遠(yuǎn)場(chǎng)方向圖如圖4所示. 從圖中可以看出,當(dāng)采樣面為整個(gè)球面時(shí),球面近遠(yuǎn)場(chǎng)變換結(jié)果和理論值吻合較好,從而證明了該球面近遠(yuǎn)場(chǎng)變換的正確性,而只采集部分近場(chǎng)區(qū)域時(shí)引入了較大的截?cái)嗾`差.

圖4 利用不同近場(chǎng)數(shù)據(jù)區(qū)域的球面近遠(yuǎn)場(chǎng)變換所得E面方向圖Fig.4 The E-plane patterns by spherical near-field to far-field transformation with different data region

現(xiàn)在考慮對(duì)近場(chǎng)數(shù)據(jù)進(jìn)行加余弦窗函數(shù)處理后,再做近遠(yuǎn)場(chǎng)變換. 取余弦窗函數(shù)的參數(shù)為x%=40%,dmp=1°,最終的計(jì)算結(jié)果如圖5所示.

圖5 對(duì)近場(chǎng)數(shù)據(jù)加窗后的球面近遠(yuǎn)場(chǎng)變換所得E面方向圖(x%=40%, dmp=1°)Fig.5 The E-plane pattern by spherical near-field to far-field transformation with near-field data weighted by cosine window function(x%=40%, dmp=1°)

從圖5可以看出,對(duì)近場(chǎng)數(shù)據(jù)加窗后再做近遠(yuǎn)場(chǎng)變換得到的遠(yuǎn)場(chǎng)方向圖更接近理論值,主瓣相對(duì)不加窗有改善,在副瓣部分效果特別明顯,其量化誤差統(tǒng)計(jì)如表1所示.現(xiàn)在改變窗函數(shù)參數(shù),其他保持不變,取x%=32%,dmp=0°,計(jì)算結(jié)果如圖6所示,誤差分析如表2所示.

圖6 對(duì)近場(chǎng)數(shù)據(jù)加窗后的球面近遠(yuǎn)場(chǎng)變換所得E面方向圖(x%=32%, dmp=0°)Fig.6 The E-plane pattern by spherical near-field to far-field transformation with near-field data weighted by cosine window function(x%=32%, dmp=0°)

方向圖值左側(cè)第一副瓣左側(cè)第二副瓣右側(cè)第一副瓣右側(cè)第二副瓣 理論值/dB-54.31-54.24-57.11-57.88 不加窗/dB-39.98-42.88-36.65-41.56 加窗/dB-44.29-56.14-56.98-60.26 誤差減小/dB4.319.4620.3313.94

表2 x%=32%, dmp=0°時(shí)誤差分析Tab.2 Error analysis when x%=32%, dmp=0°

從表1可以看出,不對(duì)近場(chǎng)數(shù)據(jù)加窗時(shí),球面近遠(yuǎn)場(chǎng)變換所得方向圖在左側(cè)第一副瓣處的值比理論值高14.33 dB,當(dāng)取窗函數(shù)參數(shù)為x%=40%,dmp=1°時(shí),對(duì)近場(chǎng)數(shù)據(jù)加權(quán)處理后,相對(duì)于理論值,誤差減少了4.31 dB. 在左側(cè)第二副瓣處,對(duì)近場(chǎng)數(shù)據(jù)加窗后球面近遠(yuǎn)場(chǎng)變換所得方向圖的值由-42.88 dB減小到-56.14 dB,相對(duì)于理論值,誤差減小了9.46 dB. 而在主瓣右側(cè), 這種方法對(duì)誤差的減小更為明顯,在右側(cè)第一副瓣處,對(duì)近場(chǎng)數(shù)據(jù)加窗后所得方向圖的值由-36.65 dB減小到-56.98 dB,相對(duì)于理論值,誤差減小了20.33 dB;同時(shí)在右側(cè)第二副瓣處,誤差減小了13.94 dB,這是因?yàn)樵谟覀?cè)采樣面邊緣附近,由于近場(chǎng)數(shù)據(jù)的不連續(xù)性引入的截?cái)嗾`差較大,而余弦窗函數(shù)在邊緣處對(duì)近場(chǎng)數(shù)據(jù)的加權(quán)程度也相應(yīng)加大,使得誤差大大減小,這正是利用余弦窗函數(shù)對(duì)近場(chǎng)數(shù)據(jù)加權(quán)的優(yōu)點(diǎn). 通過比較表1和表2可以看出,當(dāng)選取的窗函數(shù)參數(shù)不同時(shí),近遠(yuǎn)場(chǎng)變換的最后結(jié)果會(huì)不同,因此選取合適的窗函數(shù)參數(shù)可以使截?cái)嗾`差降低到最小.

當(dāng)天線最大輻射方向改變?yōu)棣?30°,φ=0°,而其他參數(shù)保持不變時(shí),設(shè)截?cái)嘟铅萾=55°,取x%=36%,dmp=3°,計(jì)算結(jié)果如圖7所示.從圖中可以看出,對(duì)包含在截?cái)鄥^(qū)域的近場(chǎng)數(shù)據(jù)加窗后再做近遠(yuǎn)場(chǎng)變換可以明顯地改變副瓣電平,使副瓣電平更接近理論值,通過計(jì)算發(fā)現(xiàn),當(dāng)天線最大輻射方向與掃描面邊界距離越近時(shí)需要加窗程度也越強(qiáng).

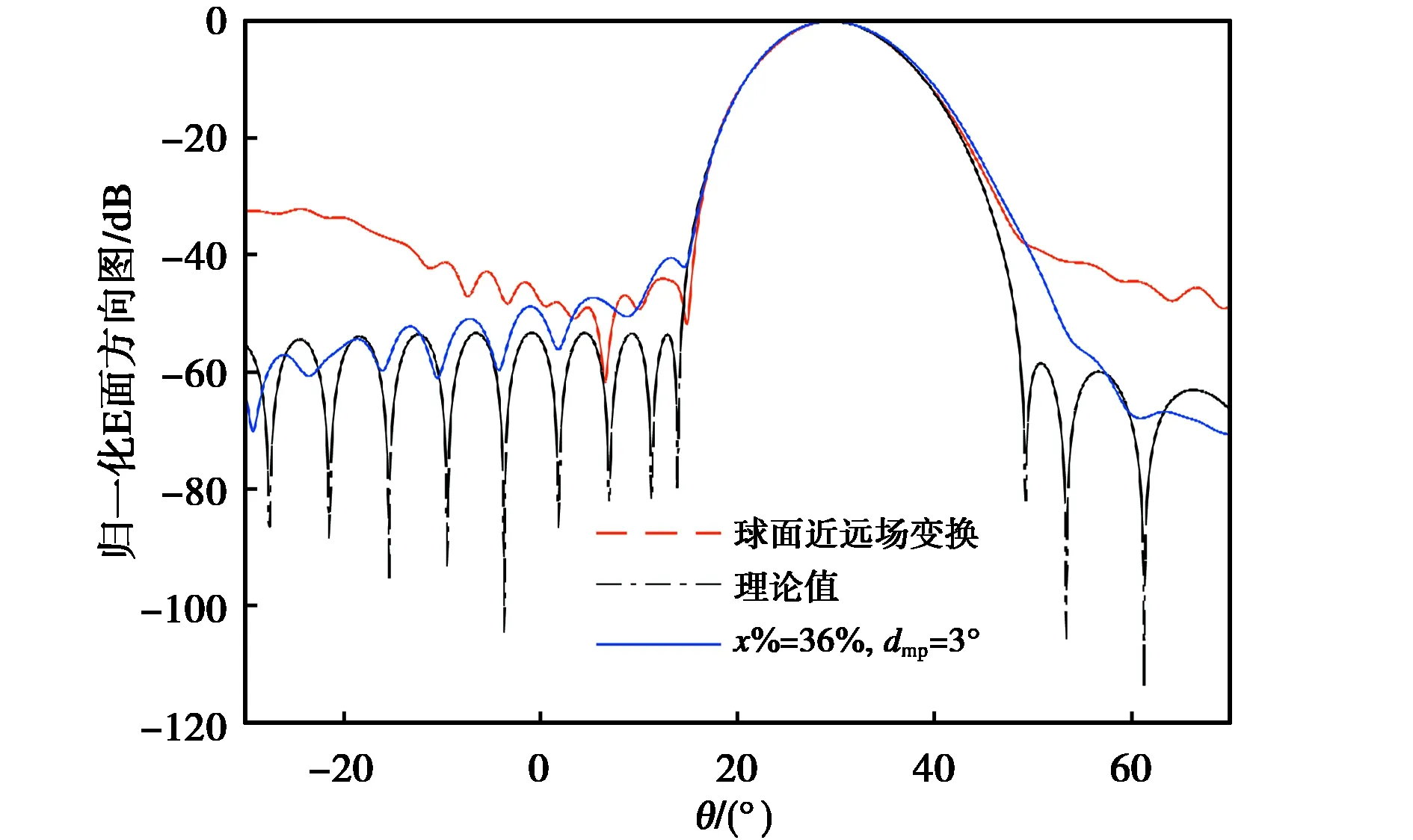
圖7 對(duì)近場(chǎng)數(shù)據(jù)加窗后的球面近遠(yuǎn)場(chǎng)變換所得E面方向圖(x%=36%, dmp=3°)Fig.7 The E-plane pattern by spherical near-field to far-field transformation with near-field data weighted by cosine window function(x%=36%, dmp=3°)

3.2 遺傳算法的應(yīng)用

通過上節(jié)的分析可以看出,對(duì)于不同的天線最大輻射方向和掃描面邊界,需要選取一個(gè)最合適的余弦窗函數(shù)參數(shù),本節(jié)利用遺傳算法來選取最優(yōu)窗函數(shù)參數(shù).

遺傳算法是一種全局隨機(jī)搜索優(yōu)化算法[13-14],本例中將遺傳算法交叉概率設(shè)為0.6,變異概率設(shè)為0.001,種群的規(guī)模大小為80,遺傳迭代的代數(shù)為400. 設(shè)余弦窗函數(shù)參數(shù)的優(yōu)化精度:x%為0.1%,dmp為1°,編碼方式為二進(jìn)制編碼.令適應(yīng)度函數(shù)為

Fitness=∑|F理論值(θ,φ)-F測(cè)量值(θ,φ)|2.

(19)

式中:F理論值(θ,φ)為理論遠(yuǎn)場(chǎng)方向圖;F測(cè)量值(θ,φ)為測(cè)量遠(yuǎn)場(chǎng)方向圖.取x%的搜索范圍為[0, 50%],dmp的搜索范圍為[0, 360°]. 天線模型與上節(jié)保持不變,取最大輻射方向?yàn)棣?30°,φ=0°,截?cái)嘟铅萾=55°,計(jì)算結(jié)果如圖8所示.

圖8 遺傳算法和窮舉法的對(duì)比Fig.8 Comparison of genetic algorithm and exhaustive method

從圖8可以看出,利用基于遺傳算法參數(shù)優(yōu)化的余弦窗函數(shù)對(duì)近場(chǎng)數(shù)據(jù)進(jìn)行加權(quán)處理能夠大大減小有限掃描面截?cái)嗾`差.遺傳算法搜索的最優(yōu)解與窮舉法得到的最優(yōu)解較為接近,但是使用遺傳算法可以減少程序運(yùn)行時(shí)間.其中主瓣左側(cè)吻合得較好,而主瓣右側(cè)吻合得相對(duì)較差,這是因?yàn)樘炀€最大輻射方向在z軸右側(cè),掃描面右側(cè)邊界處的場(chǎng)較強(qiáng),導(dǎo)致掃描面右側(cè)邊界處場(chǎng)的不連續(xù)性比左側(cè)邊界處的不連續(xù)性更強(qiáng),從而導(dǎo)致方向圖主瓣右側(cè)的截?cái)嗾`差比左側(cè)大. 表3給出了幾種不同情況下利用遺傳算法得到的最優(yōu)窗函數(shù)參數(shù)的具體取值.

表3 不同情況下的最佳參數(shù)選擇Tab.3 Selection of optimal parameters in different cases

4 結(jié) 論

本文針對(duì)相控陣天線球面近場(chǎng)測(cè)量時(shí),由于掃描面有限和波束掃描引起較大的截?cái)嗾`差這一問題,提出了利用余弦窗函數(shù)對(duì)近場(chǎng)數(shù)據(jù)進(jìn)行加權(quán)處理的方法來減小截?cái)嗾`差. 相比于其他方法,由于窗函數(shù)參數(shù)的靈活性,當(dāng)相控陣天線發(fā)生波束掃描及截?cái)嘟前l(fā)生變化時(shí),可以根據(jù)不同的情況確定最佳窗函數(shù)參數(shù)使截?cái)嗾`差降到最小,尤其是在副瓣處修正效果更明顯,具有實(shí)際工程意義. 對(duì)于窗函數(shù)參數(shù)的選取,遺傳算法的應(yīng)用可以提高參數(shù)優(yōu)化效率,得到最優(yōu)參數(shù),從而大大減小截?cái)嗾`差.