基于值函數遷移的啟發式Sarsa算法

陳建平，楊正霞，劉全，吳宏杰，徐楊，傅啟明

?

基于值函數遷移的啟發式Sarsa算法

陳建平1,2,3，楊正霞1,2,3，劉全4，吳宏杰1,2,3，徐楊5，傅啟明1,2,3

（1. 蘇州科技大學電子與信息工程學院，江蘇 蘇州 215009；2. 蘇州科技大學江蘇省建筑智慧節能重點實驗室，江蘇 蘇州 215009；3. 蘇州科技大學蘇州市移動網絡技術與應用重點實驗室，江蘇 蘇州 215009；4. 蘇州大學計算機科學與技術學院，江蘇 蘇州 215000；5. 浙江紡織服裝職業技術學院信息工程學院，浙江 寧波 315000）

針對Sarsa算法存在的收斂速度較慢的問題，提出一種改進的基于值函數遷移的啟發式Sarsa算法（VFT-HSA）。該算法將Sarsa算法與值函數遷移方法相結合，引入自模擬度量方法，在相同的狀態空間和動作空間下，對新任務與歷史任務之間的不同狀態進行相似性度量，對滿足條件的歷史狀態進行值函數遷移，提高算法的收斂速度。此外，該算法結合啟發式探索方法，引入貝葉斯推理，結合變分推理衡量信息增益，并運用獲取的信息增益構建內在獎賞函數作為探索因子，進而加快算法的收斂速度。將所提算法用于經典的Grid World問題，并與Sarsa算法、Q-Learning算法以及收斂性能較好的VFT-Sarsa算法、IGP-Sarsa算法進行比較，實驗表明，所提算法具有較快的收斂速度和較好的穩定性。

強化學習；值函數遷移；自模擬度量；變分貝葉斯

1 引言

強化學習（RL, reinforcement learning）又稱激勵學習、增強學習，是在未知、動態環境中通過agent與環境的交互實現從狀態到動作的映射，并獲得最大期望累計獎賞的一類在線學習方法[1]。在強化學習問題中，新的強化學習任務與歷史任務之間會存在某種相似性，因此可利用兩者之間的相似性來提高目標任務的學習速率，這需要運用遷移學習（TL, transfer learning）方法。1995年，遷移學習被首次以“learning to learn”的概念提出，引起學術界的廣泛關注[2]。遷移學習主要包括3個方面：遷移什么、如何進行遷移、何時進行遷移。通過這3個方面，可以使遷移學習達到提高目標任務收斂速度的目的。然而遷移學習是對以往任務中學習的經驗進行利用，從而提高目標任務的學習速率，但對于強化學習任務而言，其本身長期存在著平衡探索與利用之間關系的問題，有效地解決探索問題使agent獲得最大化環境信息的軌跡，可以加快目標任務的學習速率。

近年來，遷移學習在強化學習領域已引起廣大研究學者的關注。Ammar等[3]通過優化不同任務間可轉移的知識庫，并通過對該知識庫間不同任務構建映射關系，使新任務快速收斂。Gupta等[4]通過構建狀態空間到不變特征空間之間的映射關系，將知識映射到不變特征空間，并利用構建的映射關系實現知識的遷移，從而加快新任務的收斂速度。Laroche等[5]在假設不同任務具有相同狀態空間與動作空間的基礎上，通過添加探索因子構建新的獎賞函數，實現不同任務間的知識遷移，提高算法在后續任務中的收斂性能。Barreto等[6]提出在環境動態性不變的前提下，對不同任務之間的獎賞函數進行遷移，從而加快算法的收斂速度。

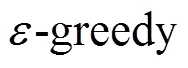
本文針對經典的Sarsa算法存在收斂速度慢的問題，提出一種基于值函數遷移的啟發式Sarsa算法（VFT-HSA）。針對經典Sarsa算法中值函數初始值的設定直接影響算法收斂速度的問題，VFT-HSA算法引入知識遷移，利用自模擬度量的方法，構造目標任務與歷史任務之間的度量關系，通過設定閾值，遷移歷史任務中的最優值函數，提高算法的收斂速度。針對大量算法問題中探索與利用不平衡的問題，VFT-HSA引入啟發式探索方法，利用貝葉斯推理，結合變分推理衡量信息增益，附加內在獎賞函數，從而提高算法的探索性能，加快算法的收斂速度。將VFT-HSA應用于Grid World問題，實驗結果表明，VFT-HSA較其他算法具有更快的收斂速度和較好的穩定性。

2 相關理論

2.1 馬爾可夫決策過程

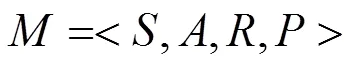
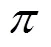
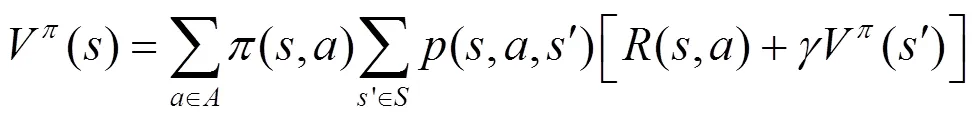
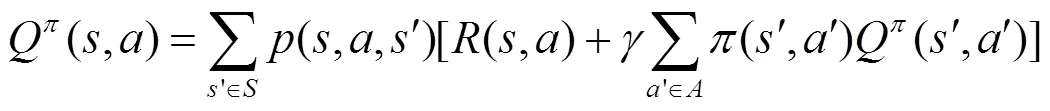
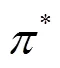
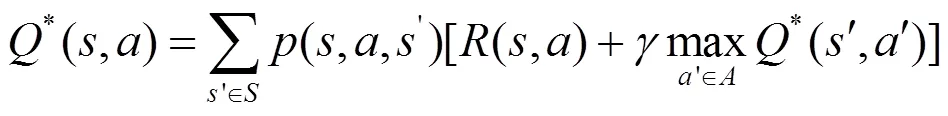
式(3)和式(4)也被稱為Bellman最優方程。

2.2 Sarsa算法

在強化學習算法中，Sarsa算法能夠在未知獎賞函數與狀態轉移函數的情況下，采用狀態動作值迭代找到最優策略，是一種在線學習算法。在Sarsa算法學習過程中，當狀態動作對被無數次訪問時，Sarsa以概率1收斂到最優策略以及最優狀態動作值函數，且策略將在有限的時間步內收斂至貪心策略。然而，Sarsa算法是一種保守算法，為了減少損失，在學習過程中會選擇相對安全的動作，這使Sarsa算法在選取動作時缺乏一定的探索，進而使Sarsa算法收斂速度相對較慢。Sarsa算法具體流程如算法1所示[1]。

算法1 Sarsa算法

2) repeat (對于每一個情節)

3) 初始化狀態

4) 在狀態下，根據行為策略選擇動作

5) repeat (對于情節中的每一步)

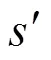
10) end repeat

11) end repeat

12) 輸出：值函數

2.3 自模擬度量

2003年，Givan等[14]首次將自模擬關系引入MDP，并利用自模擬關系度量不同MDP中狀態之間的距離。其自模擬關系可簡單表述為：若2個狀態之間滿足自模擬關系，那么2個狀態之間的最優值函數或最優動作可相互共享。

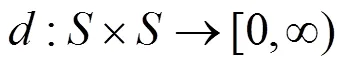
對于任意2個狀態，它們之間的自模擬關系是“是”或“非”的關系，要么滿足自模擬關系，要么不滿足自模擬關系，但在實際應用中，該方法太過于嚴苛。如果2個狀態的獎賞分布與狀態轉移概率分布極其近似，則2個狀態極其近似，根據以上條件可推測2個狀態具有相似的最優動作和最優值函數，但自模擬關系無法證明該推測。因而Ferns等[15]針對該問題，利用Kantorovich距離，提出衡量2個狀態之間相似性關系的自模擬度量方法，并得到定理1。

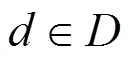
2.4 變分貝葉斯

變分貝葉斯最早由Beal[16]提出，其可應用于隱馬爾可夫模型、混合因子分析、非線性動力學、圖模型等。變分貝葉斯可較好地處理復雜統計模型。復雜統計模型由觀測變量、未知參數和潛變量這3類變量組成，其中，未知參數和潛變量統稱為不可觀測變量。

采用變分貝葉斯具有如下優點：1)將不可觀測變量的后驗概率近似成其他變量，方便不可觀測變量的推斷；2)對于一個模型，給出邊緣似然函數的下界，當邊緣似然函數值最高時，表明模型擬合程度越好，通過該方法可獲取最優模型。

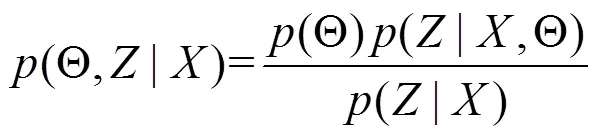
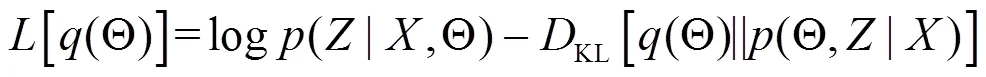
3 VFT-HAS算法思想及簡介

3.1 值函數遷移

通常，對于MDP，可以通過迭代方法求出最優狀態值函數或最優動作值函數，再由最優值函數求解最優策略。但對于每一個MDP，求解最優值函數都需要進行迭代計算，這會造成計算資源的浪費，因此考慮將已求解的歷史最優值函數用于后續的MDP中，進而求解最優值函數。若2個狀態相似，它們應該具有相似的最優狀態值函數，并利用自模擬度量關系，對相似狀態進行值函數遷移。在對值函數遷移方法進行介紹之前，先做如下假設。

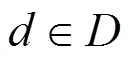
關于定理2的證明可參考文獻[17]，為了更加充分地說明定理2，給出如下說明。

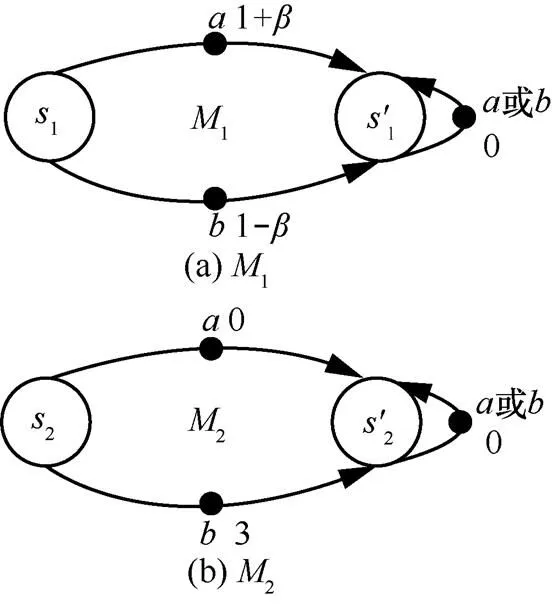
圖1 MDP狀態轉移示意

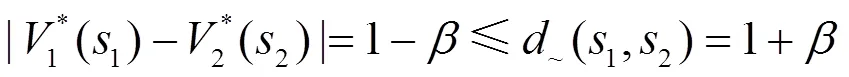
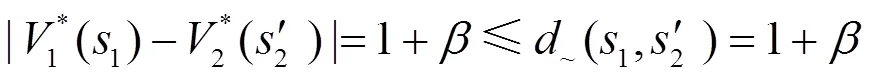
由定理2，給出不同MDP之間基于自模擬度量的值函數遷移算法，如算法2所示。

算法2 基于自模擬度量的值函數遷移算法

4) end for

5) end for

10) else

12) end if

13) end for

3.2 基于變分貝葉斯的啟發式探索

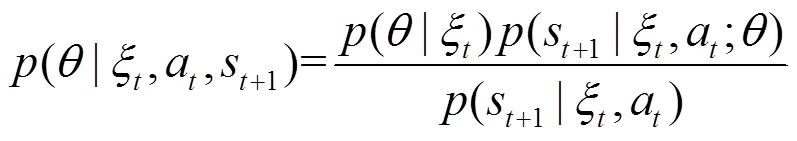
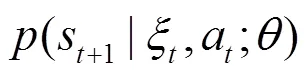
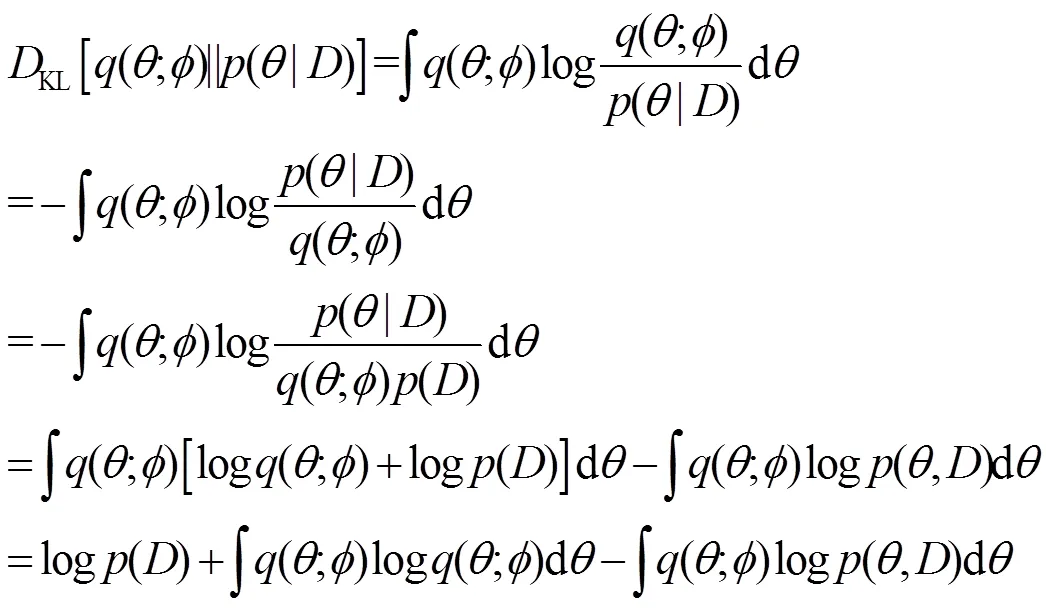
證畢。

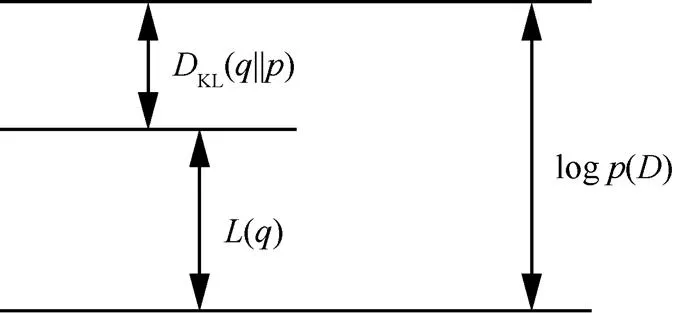
圖2 Kullback-Leibler散度關系

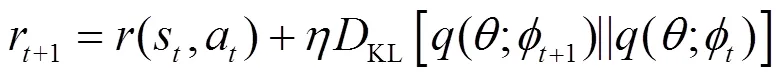
結合上述原理，給出一種改進的啟發式內部獎賞函數的更新式，如式(9)所示。

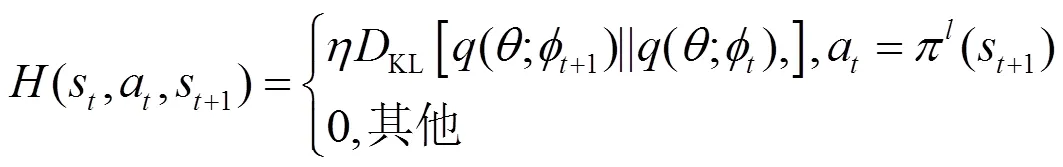
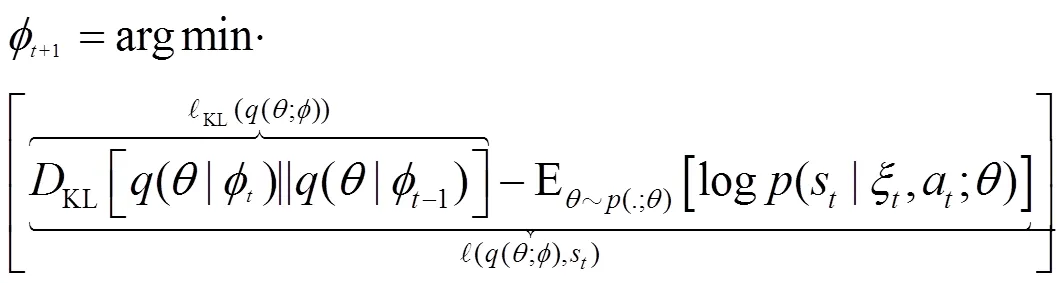
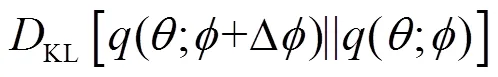
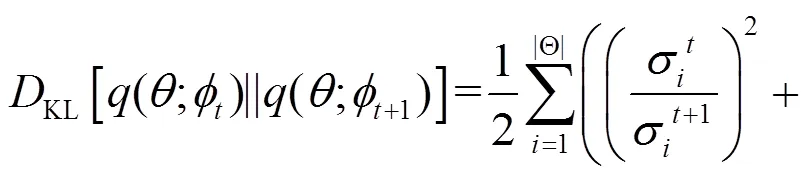
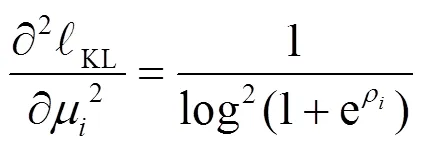
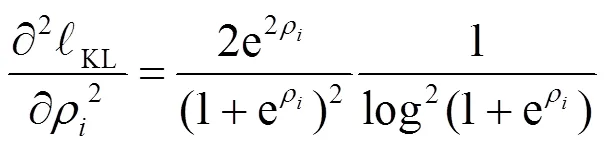
(14)

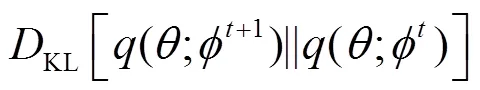
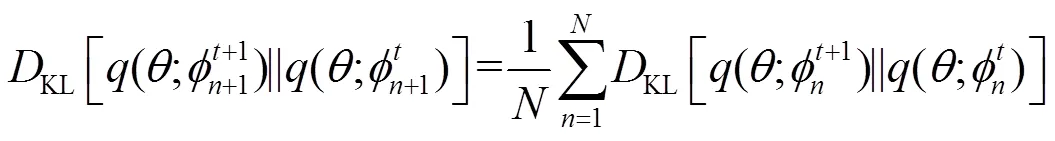
3.3 VFT-HAS簡介

基于值函數遷移的啟發式Sarsa算法主要利用自模擬度量方法對相似狀態之間的以往值函數知識進行遷移，從而提高初始化值函數的精確性，并利用變分貝葉斯理論，獲得信息增益作為內在獎賞函數進行啟發式探索，結合Sarsa算法框架，利用V-Q算法中的更新方法更新值函數[18]，提高算法收斂速度，具體如算法3所示。

算法3 基于值函數遷移的啟發式Sarsa算法

2) repeat (對于每一個情節)

4) repeat(對于情節中的每一個時間步)

12) end repeat

14) 算法終止

15) end if

18) end repeat

基于值函數遷移的啟發式Sarsa算法主要分為3個部分，第一部分利用算法2知識遷移進行初始化狀態值函數；第二部分對狀態和動作及下一個狀態進行采樣，通過變分貝葉斯理論衡量信息增益作為內部獎賞函數；第三部分在第二部分的基礎上更新狀態值函數和狀態動作值函數，求解問題最優策略，提高算法學習速率。

4 實驗及結果分析

為了研究算法的性能，將VFT-HSA應用在Grid World問題中，并針對算法收斂的速度以及算法的穩定性等方面進行分析，將VFT-HSA與Sarsa算法、Q-Learning算法、VFT-Sarsa算法[17]、IGP-Sarsa[19]算法在相同的實驗環境中重復實驗24次，取每次實驗的平均值比較各算法的性能。

4.1 Grid World問題介紹

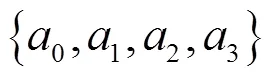
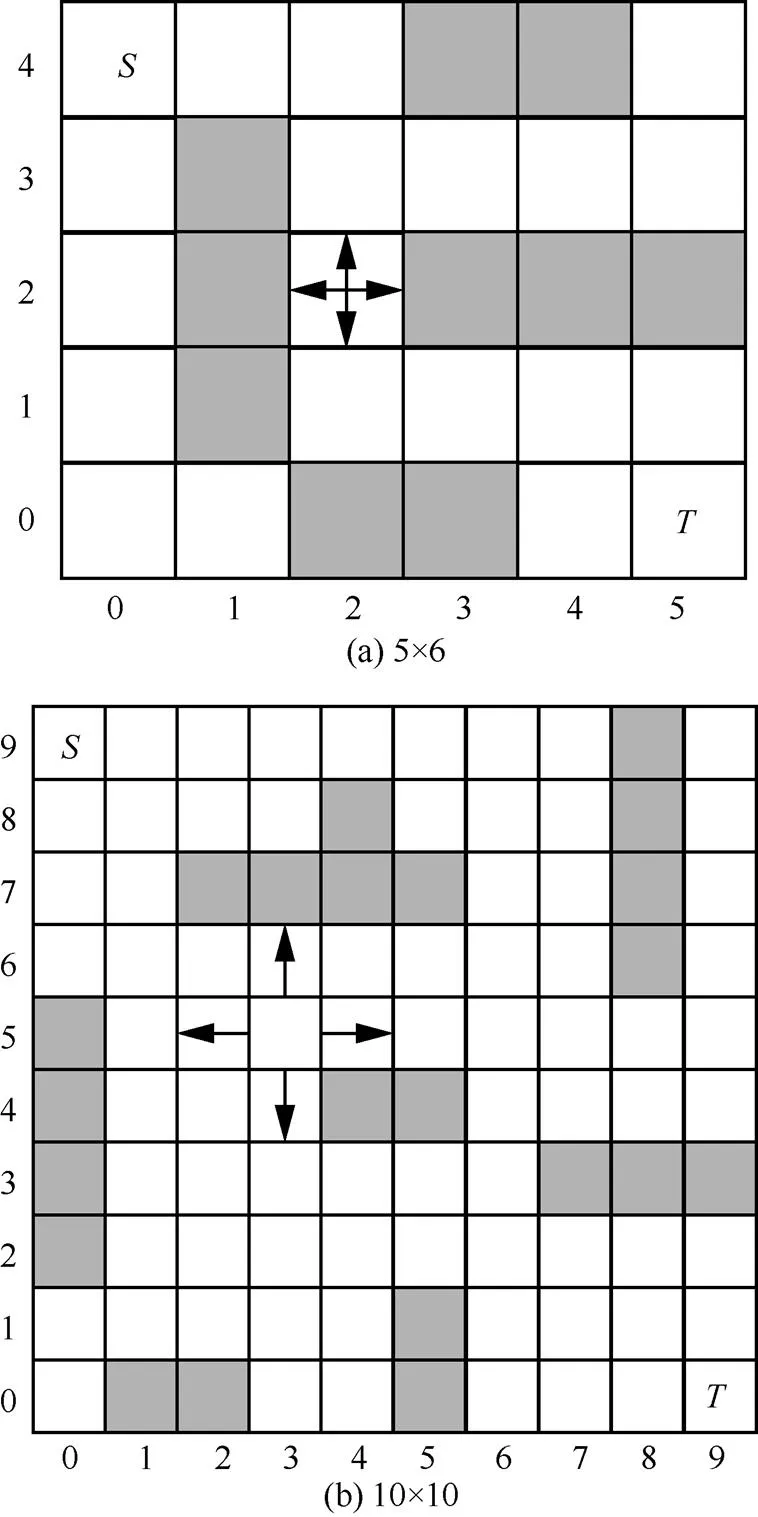
圖4 格子世界（目標MDP）

4.2 實驗設置

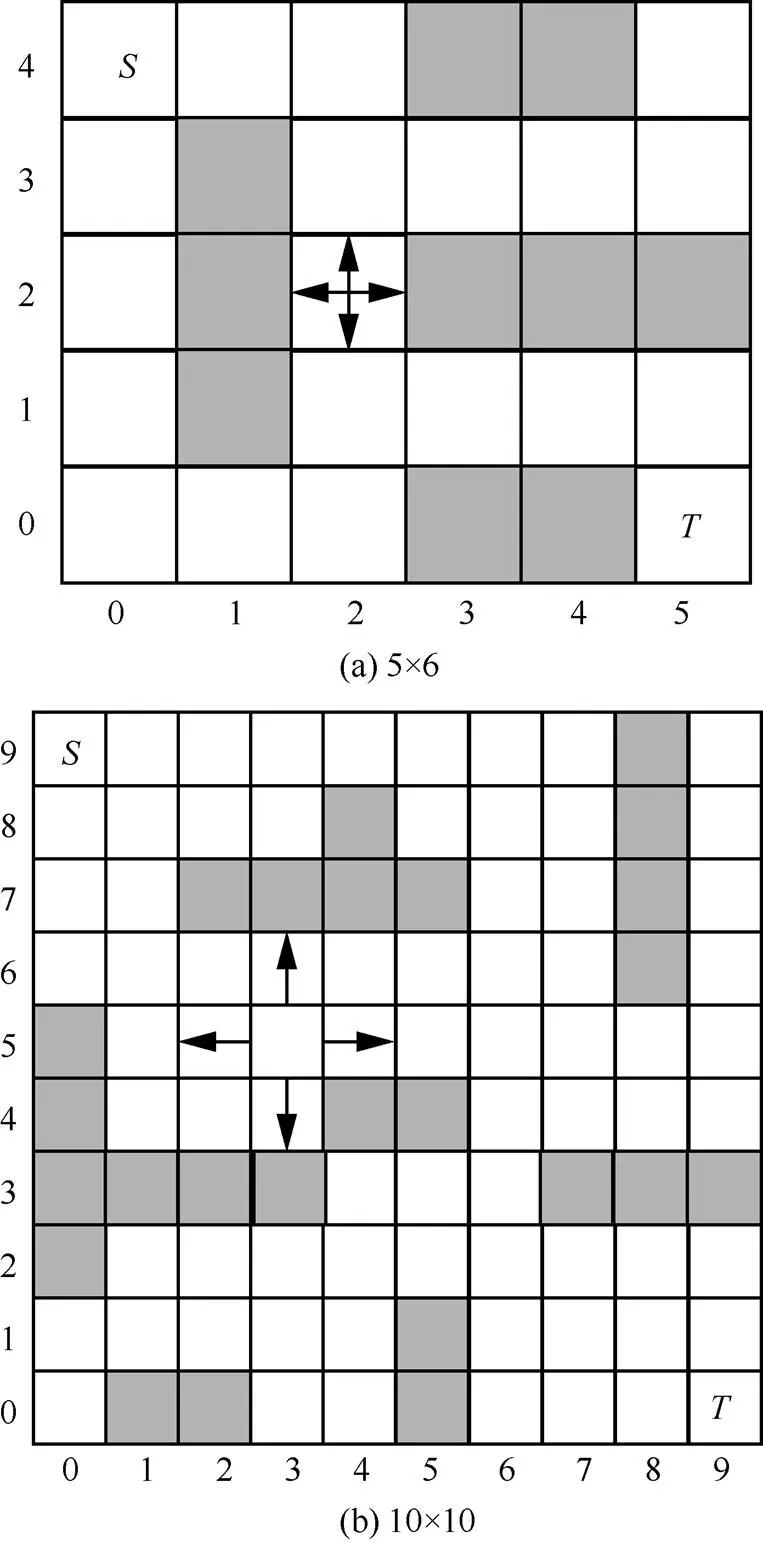
圖5 格子世界（原始MDP）

4.3 實驗分析

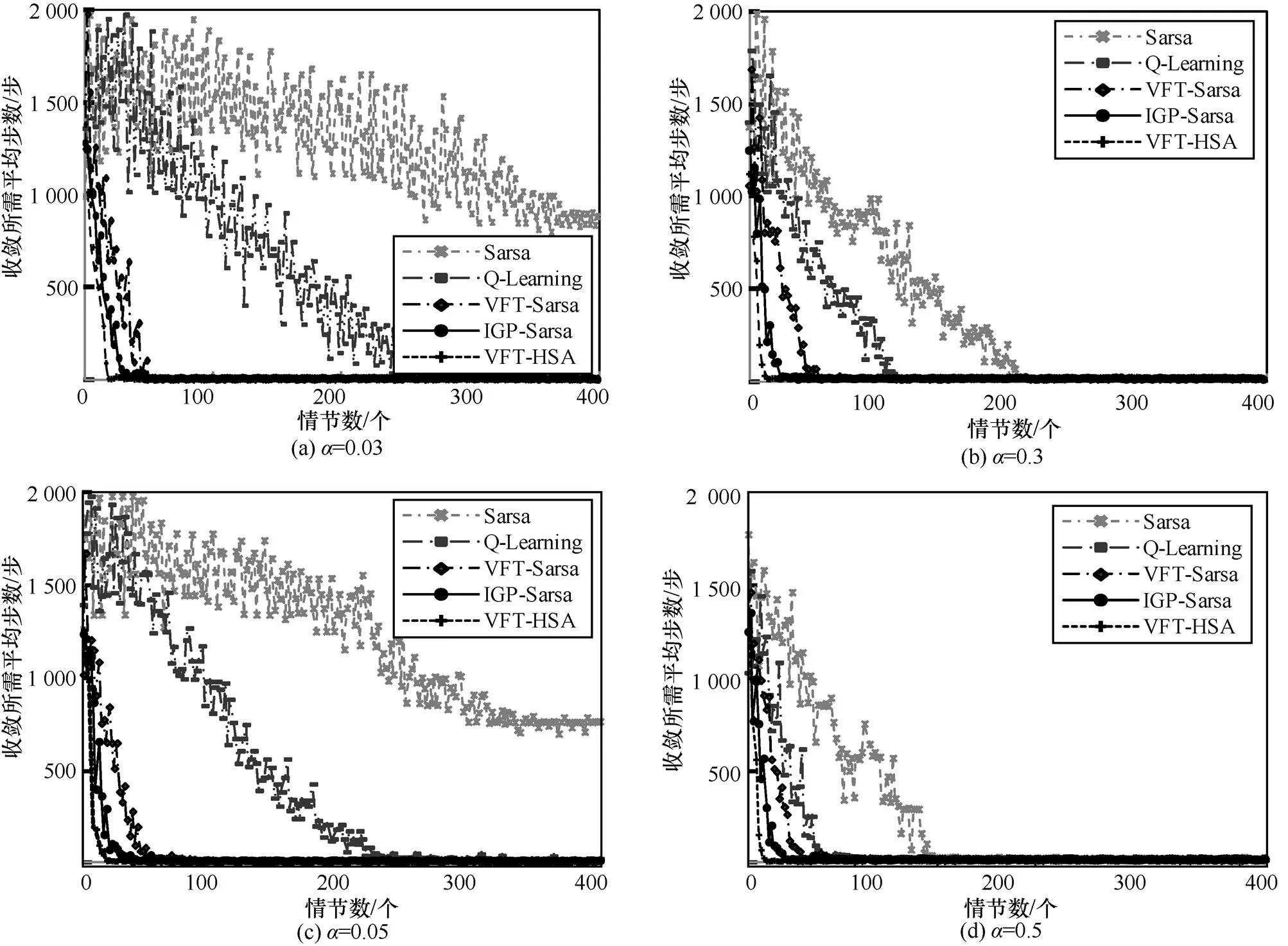
圖6 5×6的Grid World問題中5種算法性能比較

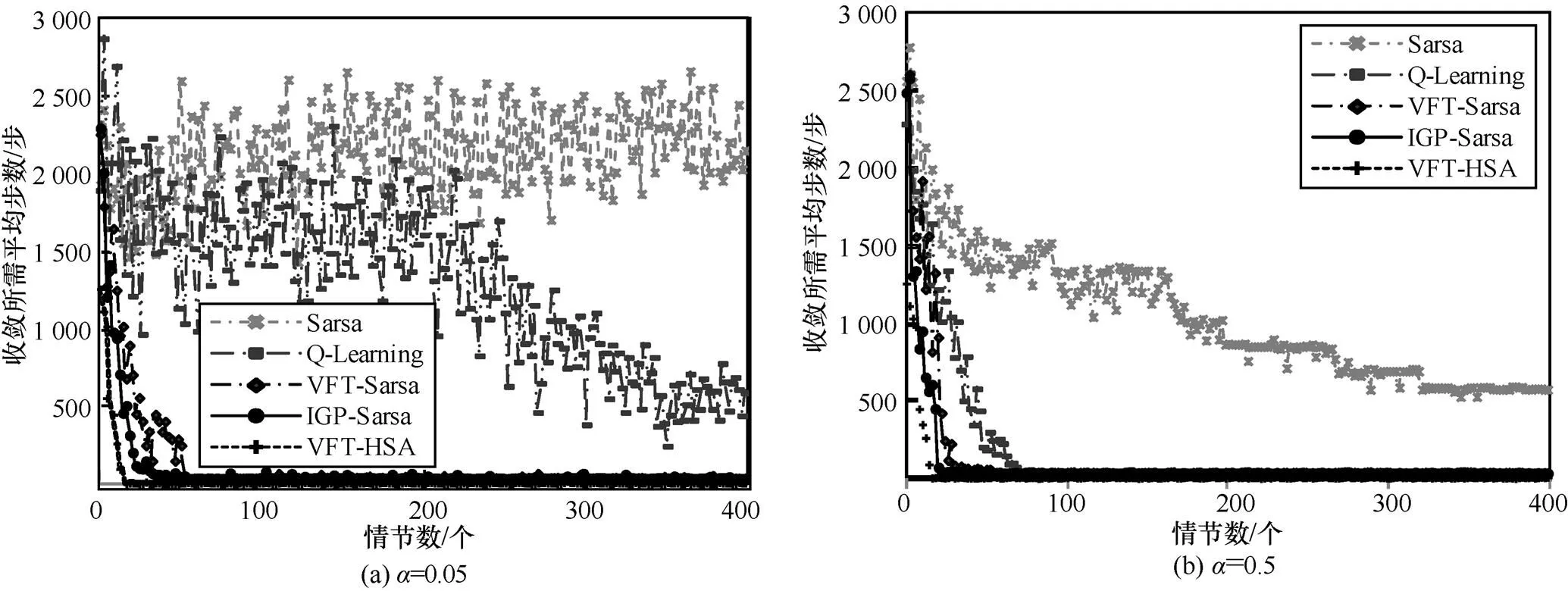
圖7 10×10的Grid World問題中5種算法性能比較

為了驗證算法采用值函數遷移方法和啟發式探索方法的收斂性能，圖8分別表示Sarsa算法、本文提出的VFT-HSA、不采用值函數遷移算法、不采用啟發式探索算法在10×10的Grid World問題中達到收斂時所需的平均時間的變化趨勢，其中，橫坐標為情節數，縱坐標為情節結束后到達目標狀態所需的時間。在實驗過程中，每一個算法都獨立執行24次，取其平均值。在圖8中，Sarsa算法不能保證較好收斂，收斂性能較差；不采用值函數遷移算法在大約40個情節處收斂，而VFT-HSA在大約30個情節處收斂，VFT-HSA相比于不采用值函數遷移算法收斂速度提升近25%，因而不采用值函數遷移算法收斂速度較慢，這是因為不采用值函數遷移算法使算法運行過程中值函數的初始值未獲得最優設置，算法收斂需要更多的樣本數量，最終導致算法收斂速度慢；不采用啟發式探索算法在大約50個情節處收斂，相比較而言，VFT-HSA收斂速度提升近40%，不采用啟發式探索算法收斂性能不及VFT-HSA，這是因為啟發式探索算法在算法收斂過程中可以提供更多的啟發式信息，加大agent探索力度，提高算法收斂速度。綜上所述，在值函數遷移方法與變分貝葉斯啟發式探索方法共同作用下，VFT-HSA的收斂速度更快，收斂性能更好。

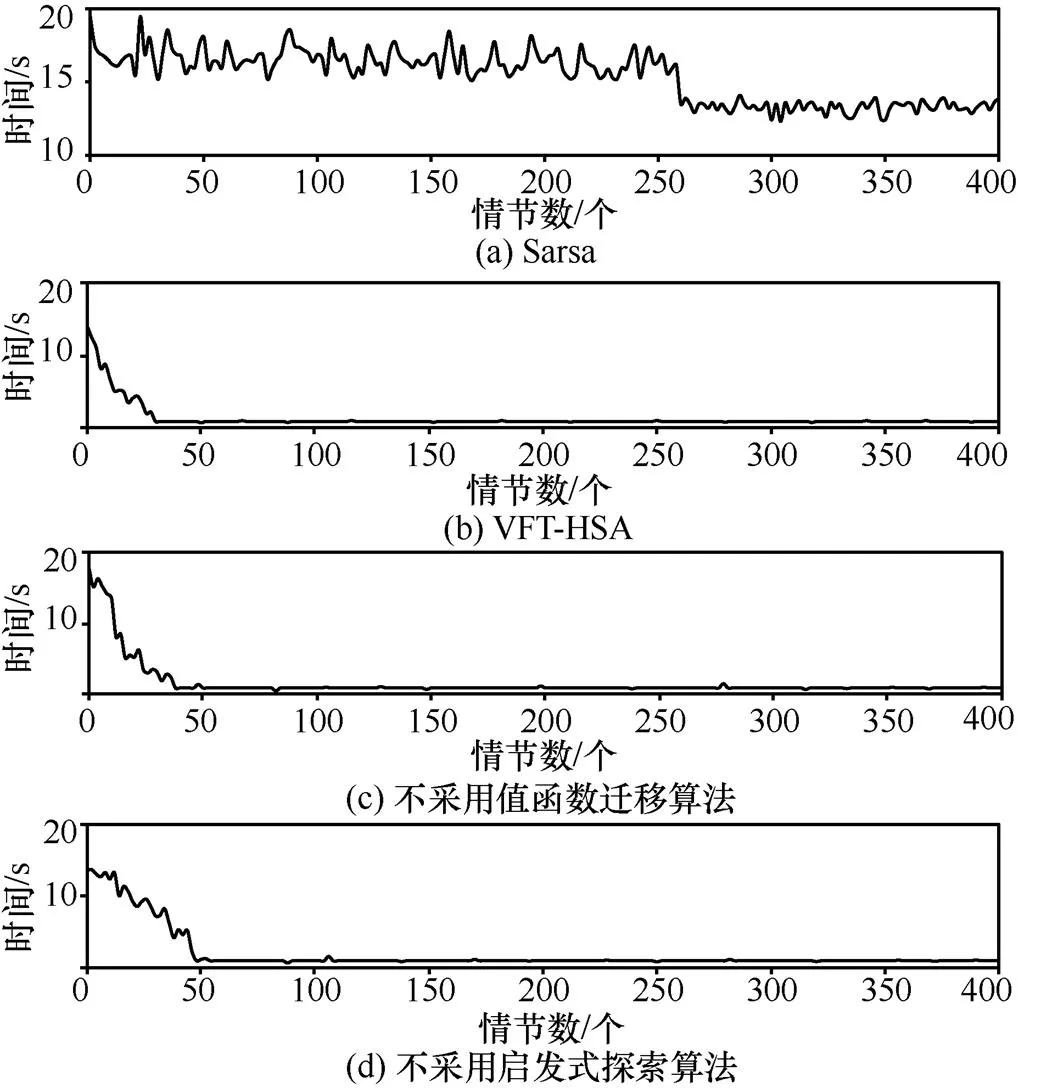
圖8 10×10的Grid World問題中4種算法的性能比較

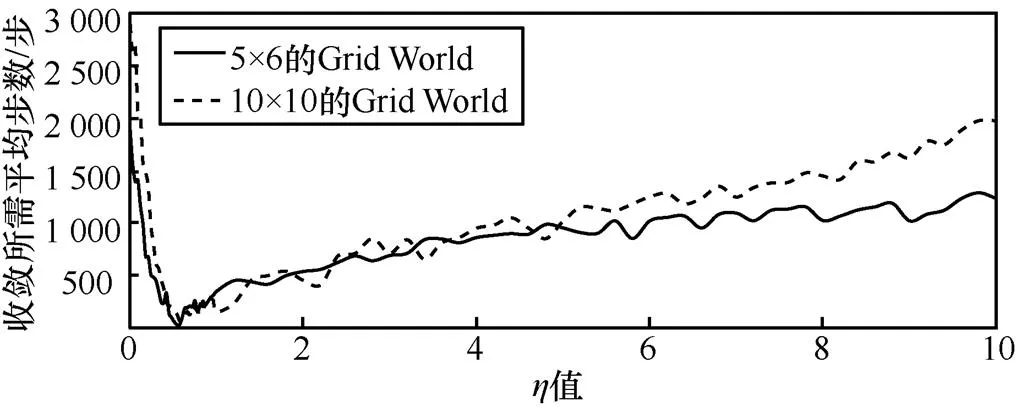
圖9 不同規模的Grid World問題中VFT-HSA取不同η值時收斂性能比較

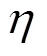
表1 不同規模的Grid World問題中VFT-HSA取不同值時收斂所需平均步數比較

5 結束語

本文針對Sarsa算法在維度較大的狀態空間和動作空間的MDP中存在收斂速度慢的問題，提出一種改進的VFT-HSA。在不同任務間具有相同狀態空間和動作空間的MDP中，該算法運用自模擬度量的方法構建不同任務下狀態之間的距離關系，當2個MDP達到一定相似度時，進行值函數知識遷移，減少算法收斂所需的樣本，提高算法的收斂性能；針對強化學習問題中存在的探索與利用的平衡問題，結合貝葉斯推理，利用變分推理獲取信息增益并用其構建內部獎賞函數模型，加大agent探索力度，提高算法收斂速度。將本文提出的VFT-HSA與Q-Learning算法、IGP-Sarsa算法用于經典的Grid World問題，實驗表明，VFT-HSA克服了經典的Sarsa算法中存在的收斂速度慢以及收斂不穩定的問題，在保證收斂精度的情況下，提高了算法的收斂速度和穩定性。

本文主要在Grid World仿真平臺中對算法進行實驗分析，實驗結果表明，本文所提算法具有較快的收斂速度和較好的收斂穩定性。本文主要對較大規模、離散的問題進行實驗分析，接下來的工作是將算法運用于更大規模的問題和連續問題中進一步驗證算法的有效性。

[1] SUTTON R S, BARTO G A. Reinforcement learning: an introduction[M]. Cambridge: MIT Press, 1998.

[2] SCHMIDHUBER J, INFORMATIK T T. On learning how to learn learning strategies[R]. Germany: Technische University, 1995.

[3] AMMAR H B, EATON E, LUNA J M, et al. Autonomous cross-domain knowledge transfer in lifelong policy gradient reinforcement learning[C]//The 15th International Conference on Artificial Intelligence. 2015: 3345-3351.

[4] GUPTA A, DEVIN C, LIU Y X, et al. Learning invariant feature spaces to transfer skills with reinforcement learning[C]//The 5th International Conference on Learning Representations. 2017: 2147-2153.

[5] LAROCHE R, BARLIER M. Transfer reinforcement learning with shared dynamics[C]//The 31th International Conference on the Association for the Advance of Artificial Intelligence. 2017: 2147-2153.

[6] BARRETO A, DABNEY W, MUNOS R, et al. Successor features for transfer in reinforcement learning[C]//The 32th International Conference on Neural Information Processing Systems. 2017: 4055-4065.

[7] DEARDEN R, NIR F, STUART R. Bayesian Q-learning[C]//The 21th International Conference on the Association for the Advance of Artificial Intelligence. 1998: 761-768.

[8] GUEZ A, SILVER D, DAYAN P. Scalable and efficient Bayes- adaptive reinforcement learning based on Monte-Carlo tree search[J]. Journal of Artificial Intelligence Research, 2013, 48(1): 841-883.

[9] LITTLE D Y, SOMMER F T. Learning and exploration in action-perception loops[J]. Frontiers in Neural Circuits, 2013, 7(7): 37-56.

[10] MANSOUR Y, SLIVKINS A, SYRGKANIS V. Bayesian incentive-compatible bandit exploration[C]//The 16th International Conference on Economics and Computation. 2015: 565-582.

[11] VIEN N A, LEE S G, CHUNG T C. Bayes-adaptive hierarchical MDPs[J]. Applied Intelligence, 2016, 45(1): 112-126.

[12] WU B, FENG Y. Monte-Carlo Bayesian reinforcement learning using a compact factored representation[C]//The 4th International Conference on Information Science and Control Engineering. 2017: 466-469.

[13] 傅啟明, 劉全, 伏玉琛, 等. 一種高斯過程的帶參近似策略迭代算法[J]. 軟件學報, 2013, 24(11): 2676-2687.

FU Q M, LIU Q, FU Y C, et al. Parametric approximation policy strategy iteration algorithm based on Gaussian process[J]. Journal of Software, 2013, 24(11): 2676-2687.

[14] GIVAN R, DEAN T, GREIG M. Equivalence notions and model minimization in Markov decision processes[J]. Artificial Intelligence, 2003, 147(1): 163-223.

[15] FERNS N, PANANGADEN P, PRECUP D. Metrics for finite Markov decision processes[C]//The 20th International Conference on Uncertainty in Artificial Intelligence. 2004: 162-169.

[16] BEAL M J. Variational algorithms for approximate Bayesian inference[D]. London: University of London, 2003.

[17] 傅啟明, 劉全, 尤樹華, 等. 一種新的基于值函數遷移的快速Sarsa算法[J]. 電子學報, 2014, 42(11): 2157-2161.

FU Q M, LIU Q, YOU S H, et al. A novel fast sarsa algorithm based on value function transfer[J]. Acta Electronica Sinica, 2014, 42(11): 2157-2161.

[18] MIERING M, HASSELT H V. The QV family compared to other reinforcement learning algorithms[C]//The 17th International Conference on Approximate Dynamic Programming and Reinforcement Learning. 2008: 101-108.

[19] CHUNG J J, LAWRANCE N R J, SUKKARIEH S. Gaussian processes for informative exploration in reinforcement learning[C]//The 20th International Conference on Robotics and Automation. 2013: 2633-2639.

Heuristic Sarsa algorithm based on value function transfer

CHEN Jianping1,2,3, YANG Zhengxia1,2,3, LIU Quan4, WU Hongjie1,2,3, XU Yang5, FU Qiming1,2,3

1. Institute of Electronics and Information Engineering, Suzhou University of Science and Technology, Suzhou 215009, China 2. Jiangsu Province Key Laboratory of Intelligent Building Energy Efficiency, Suzhou University of Science and Technology, Suzhou 215009, China 3. Suzhou Key Laboratory of Mobile Networking and Applied Technologies, Suzhou University of Science and Technology, Suzhou 215009, China 4. School of Computer Science and Technology, Soochow University, Suzhou 215000, China 5. Institute of Information Engineering, Zhejiang Fashion Institute of Technology College, Ningbo 315000, China

With the problem of slow convergence for traditional Sarsa algorithm, an improved heuristic Sarsa algorithm based on value function transfer was proposed. The algorithm combined traditional Sarsa algorithm and value function transfer method, and the algorithm introduced bisimulation metric and used it to measure the similarity between new tasks and historical tasks in which those two tasks had the same state space and action space and speed up the algorithm convergence. In addition, combined with heuristic exploration method, the algorithm introduced Bayesian inference and used variational inference to measure information gain. Finally, using the obtained information gain to build intrinsic reward function model as exploring factors, to speed up the convergence of the algorithm. Applying the proposed algorithm to the traditional Grid World problem, and compared with the traditional Sarsa algorithm, the Q-Learning algorithm, and the VFT-Sarsa algorithm, the IGP-Sarsa algorithm with better convergence performance, the experiment results show that the proposed algorithm has faster convergence speed and better convergence stability.

reinforcement learning, value function transfer, bisimulation metric, variational Bayes

TP391

A

10.11959/j.issn.1000?436x.2018133

陳建平（1963?），男，江蘇南京人，博士，蘇州科技大學教授，主要研究方向為大數據分析與應用、建筑節能、智能信息處理。

楊正霞（1992?），女，江蘇揚州人，蘇州科技大學碩士生，主要研究方向為強化學習、遷移學習、建筑節能。

劉全（1969?），男，內蒙古牙克石人，博士，蘇州大學教授、博士生導師，主要研究方向為智能信息處理、自動推理與機器學習。

吳宏杰（1977?），男，江蘇蘇州人，博士，蘇州科技大學副教授，主要研究方向為深度學習、模式識別、生物信息。

徐楊（1980?），女，河北深州人，浙江紡織服裝職業技術學院講師，主要研究方向為數據分析與應用、智能化與個性化教學。

傅啟明（1985?），男，江蘇淮安人，博士，蘇州科技大學講師，主要研究方向為強化學習、深度學習及建筑節能。

2018?03?22；

2018?07?13

傅啟明，fqm_1@126.com

國家自然科學基金資助項目（No.61502329, No.61772357, No.61750110519, No.61772355, No.61702055, No.61672371, No.61602334）；江蘇省自然科學基金資助項目（No.BK20140283）；江蘇省重點研發計劃基金資助項目（No.BE2017663）；江蘇省高校自然科學基金資助項目（No.13KJB520020）；蘇州市應用基礎研究計劃工業部分基金資助項目（No.SYG201422）

The National Natural Science Foundation of China (No.61502329, No.61772357, No.61750110519, No.61772355, No.61702055, No.61672371, No.61602334), The Natural Science Foundation of Jiangsu Province (No.BK20140283), The Key Research and Development Program of Jiangsu Province (No.BE2017663), High School Natural Science Foundation of Jiangsu Province (No.13KJB520020), Suzhou Industrial Application of Basic Research Program Part (No.SYG201422)