調水工程中梯級泵站的優化調度

趙文竹

（山東省膠東調水工程博興管理站，山東 博興 256599）

本文介紹的數學模型主要針對調水為目的的梯級泵站系統，進行數學建模依據流域的實際水利情況、現有工程和未來的規劃方案等，設置各級泵站間的區間來水量和用水量兩項參數進行計算輔助。

1 水位優化理論基礎

1.1 提水揚程與泵站效率及功率的關系

梯級泵站的作用是，通過大型水泵將需要調配的水從水源水位提升到目標水位，如果沿途的水量損失可以忽略，則整個過程水泵需要對水做的總功為：W=mgH=mg（H1+…+Hi+…Hn）

式中W為總功；H為梯級泵站的總揚程；Hi分別表示各級泵站的揚程。

相應的梯級泵站總功率為：

式中ηZ表示當揚程為H時梯級泵站系統的總效率；ηi表示對應揚程下的各級泵站的效率值。當第i級泵站的機組臺數大于1時有：

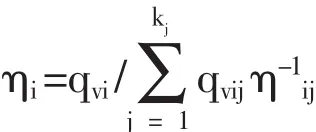
結合相關參數，對公式進行整理可得：

其中：

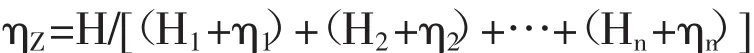
由以上公式，可知各泵站的效率和揚程有關，因此梯級泵站水位的優化工作便轉化為了通過相關數學模型的計算，找出最優水位組合，從而滿足設計要求，讓整個系統達到總效率最高、總能耗最低。

1.2 水位情況及流量平衡計算

本文采用了“系統總能耗最小”作為優化的目標。在所有可能的影響因素中，流量和揚程是其中最為關鍵的兩個因素。梯級調水工程與各梯級站的抽水流量直接相關，每一級泵站的進水量都可分為兩個部分，一部分提供給下一級泵站，而另一部分還要供給本區域的日常用水，每一級泵站的總流量 qvi，t的公式：qvi，t=qvi+1，t+q′vi，t

泵站的揚程由泵站的進、出水位及水頭損失決定：Hi，t=hi2，t-hi1，t+Δhi，t

2 建立水位優化模型

當水量變化處于一個相對較短的時間變化區間內各泵站的用水流量qvi，t保持不變，所以我們用q′vi將其代替，從而建立一個以總功率最小為目標，每一級泵站的總流量為自變量的水位輸出模型，寫成函數關系式如下：

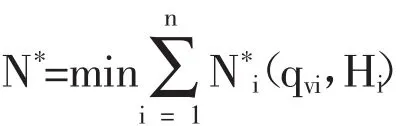
結合相關數據及優化條件可得出每一級泵站內優化數學模型：

3 梯級泵站水位優化模型求解

3.1 設計并優化總揚程與各梯級泵站

1）確定階段變量，即泵站的級數值；

2）賦予狀態變量，即從1級泵站到i級泵站的揚程 Hi，當且僅當 i=n，有 H′n＝hn2-h11。其中 h11為首級泵站的進水水位，該數據根據水源水位高度和泵的抽水量計算得出。調水工程的水源為大型水源，則該數據應由實際測量得出；

3）確定第i級泵站的揚程數值；

4）確定狀態轉移方程：H′i＝H′i+1-Hi；

5）根據整個優化模型確定逆序遞推方程：

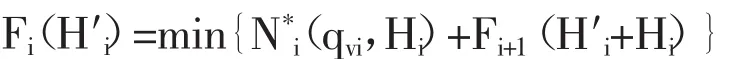
3.2 各級泵站站內機組的優化

本文采用了之前分配給各級泵站的水位揚程數據進行最優解求算。如果各級泵站中有機組的性能相同，則可以按照平均分配原則制訂優化方案，并進行最優化求解。具體操作如下：將各級泵站優化后得到的能耗數據，返回梯級泵站大系統進行優化協調操作，并不斷將得到的新的離散水位數據輸入系統進行循環計算，通過計算最終得到系統的最優值。

4 實際應用舉例

某調水工程中的梯級泵站有4級，所有泵站設備參數見表1，并已知所有水泵的功率、揚程特性曲線。首級泵站的進水水位為18.5～21.0m，最后一級泵站的出水水位為43.0～44.0m；中間各級泵站的受水區水位分別是24.0～26.0m，29.2～31.5m和 36.7～39.0m。

表1 各級泵站設備參數

跟上述數據可知在某一短時調度時段，首級泵站進水位與末級泵站的出水位并無明顯變化，將其視為一個固定的邊界條件。所以在梯級泵站運行初期，可以先啟動首級泵站的機組，讓其抽水量大于下一級泵站，此時兩級泵站之間的水位會逐漸達到最優，屆時再停車該泵站的機組。

接下來進行具體計算，假設某時刻的抽水流量是10m3/s，各級泵站的初始狀態參數見表2，計算方法如前文所述，計算結果見表2。在此次模擬計算中計算精確度為±1 cm，離散步長為1 cm，因此水位數據被分成200份離散值。應用第3小節所述方法和流程，利用VB對計算程序進行編寫并實現計算和優化，其結果如表2所示。

表2 各級泵站初始狀態參數和優化計算結果

5 結語

1）以上所有計算均基于一定的假設，因此在實際編程計算時，可做相應地簡化。

2）在泵站的不同運行時段，各級泵站的進出水水位可能發生細微的變化，此時要據具體變化情況做出相應的優化。

3）最終結果的精確性對整個泵站的運行效率產生直接影響，所以在進行計算時，必須找出最佳的離散度，以滿足計算所要求的精度。

4）從表2可以看出，經過優化后各級泵站的功率大約減小了1.70%，滿足經濟性要求。