黃河中游吳堡一龍門段河道洪水概化預報研究

黃華平 侯博 梁忠民 李彬權(quán) 王軍

摘要：將洪水過程模式概化與支持向量回歸機相結(jié)合，提出了一種逐時段更新的河道洪水概化預報方法。以黃河中游吳堡一龍門段河道洪水預報為例，根據(jù)龍門站1980-2000年28場洪水過程資料概化出典型洪水模式，采用支持向量回歸機算法構(gòu)建洪峰流量與洪水歷時的預報模型，根據(jù)逐時段洪峰流量/洪水歷時的預報結(jié)果，對概化的典型洪水模式進行縮放，實現(xiàn)了龍門站洪水過程主要特征的概化預報。對2001-2006年5場洪水的預報檢驗結(jié)果表明：隨著逐時段資料的更新，該方法的預報精度逐步提升，且漲水階段的預報結(jié)果已能較好地展示整場洪水過程的發(fā)展趨勢。

關(guān)鍵詞：支持向量回歸機：概化預報：洪水：吳堡一龍門區(qū)間：黃河中游

中圖分類號：TV122；TV882.1

文獻標志碼：A

doi：10.3969/j.issn.1000-1379.2018.06.008

1 引言

黃河中下游洪水陡漲陡落，含沙量變幅大，河床沖淤變化劇烈，河道洪水演進規(guī)律的復雜性給汛期防洪帶來嚴重影響[1-2]。目前，關(guān)于黃河中下游河道洪水演進規(guī)律研究已有大量成果，如：趙連軍等[3]采用非恒定洪水演進數(shù)學模型，在黃河下游河道開展了汛期洪水演進預測及演進實時作業(yè)預報：劉華振等[4]采用馬斯京根分段連續(xù)演算法，模擬了黃河吳龍區(qū)間（吳堡一龍門區(qū)間）洪水過程：賀莉等[5]采用一維水動力學模型分析了黃河吳堡一潼關(guān)河段洪水傳播時間與洪水量級的關(guān)系：李肖男[6]等采用三維水沙數(shù)學模型，對黃河下游花園口一艾山河段不同治理方案下場次洪水的演進過程、河道沖淤及分洪退水過程進行了模擬計算：張曉雷等[7]采用平面二維水沙數(shù)學模型，在黃河下游河道現(xiàn)存生產(chǎn)堤條件下對典型洪水進行了模擬計算。

考慮到黃河中下游河道洪水預報的復雜性，本文將洪水過程模式概化與支持向量回歸機（ SupportVeCtor machine for Regression，SVR）相結(jié)合，構(gòu)建了一種簡單、快速的河道洪水概化預報方法。選取1980-2000年28場洪水作為率定資料概化了典型洪水過程，并訓練了基于支持向量回歸機的洪峰流量/洪水歷時預報模型，將2001-2006年間的5場洪水作為驗證資料，采用該方法進行了預報檢驗，并將預報結(jié)果與實測洪水過程進行了比較。

2 洪水模式概化

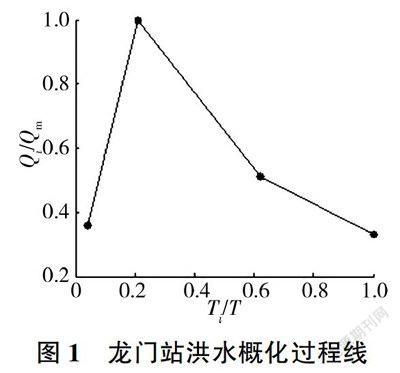
概化洪水過程線是根據(jù)待預報站點的實測洪水過程線資料進行綜合分析后得出的具有一定代表性的洪水過程線模式[8]。具體做法：首先，將各場次洪水過程線繪在同一幅圖上，縱坐標表示流量相對數(shù)Q/Q_m（Q_i為i時刻的流量，Q_m為最大流量），橫坐標表示時間相對數(shù)T_i/T（T_i為i時刻的洪水歷時，T為洪水過程總歷時），然后將峰現(xiàn)時間重疊在一處，選用其中常見且能概括該站洪水形狀特征的平均過程線作為概化過程線。龍門站1980-2000年28場洪水過程線的概化結(jié)果見圖1。

3 基于SVR的洪峰/歷時預報模型

3.1 支持向量回歸機

SVR是建立在支持向量機（SVM）上的回歸算法，其基本思想是用少數(shù)支持向量代表整個樣本集，利用非線性映射ψ（x）將低維非線性函數(shù)估計問題轉(zhuǎn)換為高維線性函數(shù)估計問題[9-10]。

已知一個訓練集X={（X1，y1），（x2，y2），…，（x_n，y_n）} Rⁿ×R，設其在高維特征空間的線性回歸函數(shù)為

f（x）=[ω，ψ（x）]+b （ω，x ∈Rⁿ；6∈R） （1）式中：x為樣本輸入；ψ（x）為x的非線性映射；[ω，ψ（x）]為ψ（x）的線性多項式；ω為多項式系數(shù)；b為截距。

可以把不敏感損失函數(shù)ε范圍內(nèi)的回歸估計問題定義為對一個損失函數(shù)進行風險最小化的問題，即最優(yōu)的回歸函數(shù)是在一定約束條件下的最小化規(guī)則化風險泛函，通過引入非負松弛變量ξ_i：及ξ*_i，最小化規(guī)則化風險泛函可以描述為

.

式中：C為誤差懲罰系數(shù)。

此時約束條件為

誤差懲罰參數(shù)C可起到調(diào)節(jié)模型復雜度和訓練誤差的作用，取值太小或太大，將出現(xiàn)“欠學習”或“過學習”現(xiàn)象，使訓練誤差增大、泛化能力減弱；核參數(shù)σ反映了訓練樣本數(shù)據(jù)的分布特性，確定了局部領(lǐng)域的寬度。因此，SVR回歸問題的推廣性能取決于誤差懲罰參數(shù)C與核參數(shù)σ。由于遺傳算法（ GenetiC Algo-rithm，GA）在復雜的優(yōu)化問題中只需構(gòu)造一個適應度函數(shù)，就可通過選擇、雜交、變異等遺傳機制，完成對問題最優(yōu)解的白適應搜索過程，且算法成熟，在水文中應用廣泛，因此本次選擇構(gòu)建GA-SVR算法進行參數(shù)優(yōu)選，這樣既可保證參數(shù)的準確性，又可保證計算的時效性。算法流程見圖2。

3.2 預報因子挑選

龍門站洪水的主要來源分為三類：干流上游來水、區(qū)間人流及無控區(qū)域降水。研究中將吳堡站對應場次洪水作為干流上游來水，選取白家川、甘谷驛、后大成、裴溝和延川站作為支流典型站，由于這些站點匯流至龍門站的歷時大致相同，因此將這5個站的流量合并作為區(qū)間人流量。甘谷驛站以下至龍門站區(qū)域為無控區(qū)域，選取該區(qū)域內(nèi)10個雨量站（柏坡底、大寧、河底、吉縣、李家山、王家窯、張川河、桐灣、郭家垛、坡頭），采用泰森多邊形法計算該區(qū)域面平均雨量。采用相關(guān)系數(shù)顯著性檢驗表確定初選因子，之后采用逐步回歸法對初選因子作進一步篩選，確定最終的預報因子。洪峰流量/洪水歷時的預報因子見表1。

3.3 模擬與驗證結(jié)果

將Matlab作為編程平臺，挑選出龍門站1980-2006年33場洪水的對應預報因子。其中：1980-2000年的28場洪水作為率定資料，用于訓練GA -SVR模型：2001-2006年的5場洪水作為驗證資料，采用訓練完畢的GA -SVR模型對其洪峰流量及洪水歷時進行預測。選用相對誤差作為模型的評價指標，率定期及驗證期模型的計算結(jié)果見表2、表3。

由表2、表3可看出，在28場率定洪水中，洪峰流量相對誤差小于20%的有23場，洪水歷時相對誤差小于20%的有16場，洪峰流量和洪水歷時的合格率分別為82.1%和57.1%：5場驗證洪水中，洪峰流量相對誤差小于20%的有4場，洪水歷時相對誤差小于20%的有3場，洪峰流量和洪水歷時的合格率分別為80.0%和60.0%。結(jié)果表明，采用GA-SVR模型對龍門站洪水的洪峰及歷時進行預報是可行的。

4 洪水過程預報示例

本文引人逐時段（△t=l h）更新預報的方法，具體步驟如下。

（1）從洪水起漲時刻開始預報，挑選預報因子時，將吳堡站和區(qū)間人流對應場次洪水初始時刻至當前時刻的最大洪水流量作為該站（或區(qū)間）當前時刻的洪峰流量，初始時刻至當前時刻的洪量作為該站（或區(qū)間）當前時刻的洪量，初始時刻至當前時刻的歷時作為該站（或區(qū)間）當前時刻的洪水歷時，其他預報因子進行類似處理。

（2）將已確定的預報因子導人已訓練完畢的洪峰流量/洪水歷時預報模型中，預報當前時刻的洪水洪峰及洪水歷時。

（3）使用當前時刻預報的洪峰流量及洪水歷時，對已概化的龍門站典型洪水模式進行相應縮放，將縮放結(jié)果作為當前時刻的洪水過程預報結(jié)果。

（4）隨著洪水資料的不斷更新，重復步驟（1）～步驟（3），直至整場洪水結(jié)束。

以龍門站“20040727”洪水為例，分別列出從洪水起始時刻起（作為0時刻）第2、第6、第13及第27時刻的洪水過程預報結(jié)果，見圖3。

由圖3可以看出：①隨著時段推移，資料不斷更新，逐時段更新預報方法結(jié)果的精度呈上升趨勢，整體體現(xiàn)出“越報越好”的預報效果：②在洪峰出現(xiàn)時刻前（第6時刻），預報的洪水流量過程與實測流量過程相差已較小，說明在洪水起漲時段，該方法的預報結(jié)果已能較好地描述整場洪水的發(fā)展過程：③洪峰預報精度隨著時段推移不斷提升，之后趨于平穩(wěn)：④對于洪水歷時的預報，隨著時段推移其吻合程度總體呈穩(wěn)步上升趨勢，直至該場洪水結(jié)束。

5 結(jié)語

將洪水過程模式概化與支持向量回歸機相結(jié)合，提出了一種逐時段更新的河道洪水概化預報方法。選取龍門站1980-2000年間的28場洪水作為率定資料，用于概化典型洪水過程及構(gòu)建基于GA-SVR的洪峰流量/洪水歷時預報模型，并對2001-2006年的5場洪水進行了預報檢驗。結(jié)果表明：①隨著洪水資料的不斷更新，該方法的預報精度呈上升趨勢，整個預報過程呈現(xiàn)出“越報越好”的預報效果：②實時預報過程中，隨著時段推移，洪峰流量預報精度逐漸上升，之后趨于平穩(wěn)，在洪水過程的漲水段，該方法已能較好地體現(xiàn)整場洪水過程的發(fā)展趨勢。

本文研究的是一種洪水過程的概化預報方法，側(cè)重的是洪峰、洪水過程主體形狀的預報，具有簡單.快速等特點。但是，本文僅概化了單峰洪水模式，對于模式更復雜的洪水（如復式洪水過程）還需要進一步研究。

參考文獻：

[1]趙衛(wèi)民.黃河中下游暴雨洪水情報預報原型系統(tǒng)[J].人民黃河，1994，16（8）：12-14.

[2]李彬權(quán)，牛小茹，梁忠民，等.黃河中游干旱半干旱區(qū)水文模型研究進展[J].人民黃河，2017，39（3）：1-4.

[3] 趙連軍，江恩惠，董其華，等.數(shù)學模型在黃河下游河道洪水演進預報中的應用[J].四川大學學報（T程科學版），2007，39（1）：6-12.

[4] 劉華振，劉俊，左君，等.馬斯京根法在黃河吳堡一龍門區(qū)間洪水演算中的應用[J].水電能源科學，2012，30（6）：53-55.

[5] 賀莉，傅旭東.黃河吳堡一潼關(guān)河段洪水傳播時間的沿程分布[J].南水北調(diào)與水利科技，2012，10（1）：18-26.

[6]李肖男，張紅武，鐘德鈺，等.黃河下游河道治理三維數(shù)值 模擬研究[J].水利學報，2017，48（ 11）：1280-1292.

[7] 張曉雷，張英克，孫東坡.黃河下游典型河段灘槽分界二維洪水數(shù)值模擬[J].水利水電技術(shù)，2013，44（7）：120.

[8]梁忠民，鐘平安，牮家鵬.水文水利計算[M].北京：中國水利水電出版社.2008：111- 112.

[9] VAPNIK V.Estimation of Dependences Based on EmpiricalData[M]. New York： Springer Science&Business Media，2006：181-230.

[10]

VAPNIK V.The Nature of Statistical Leaming Theory[M].New York： Springer Science&Business Media， 2013：267-287.