含沙量監測的wavelet—Kalman多尺度融合研究

付立彬 劉明堂 王麗 秦澤寧 楊陽蕊

摘要：為解決黃河含沙量監測時傳感器易受環境因素影響的問題，簡述了音頻共振法測量含沙量的原理，探討了音頻共振傳感器的諧振頻率和含沙量監測之間的關系，提出了貫序式wavelet-Kalman多尺度融合模型，對音頻共振傳感器的諧振頻率進行小波分解，把含沙量數據組成貫序式數據塊進行多尺度分析，提取含沙量信號序列中的突變值，建立了Kalman融合方程，將溫度信息作為控制信號，消除了環境因素對含沙量監測的影響，并進行了含沙量測量的反演和誤差分析。結果表明：貫序式wavelet-Kalman多尺度融合模型能夠有效地消除環境影響，提高系統測量的精度和穩定性，平均絕對誤差為3.95kg/m2，均方根誤差為3.13kg/m3，比其他反演模型的誤差小。

關鍵詞：音頻共振法；貫序式；小波多尺度分析；卡爾曼融合；含沙量監測

中圖分類號：P335 文獻標志碼：A doi：10.3969/j.issn.1000-1379.2018.09.005

懸浮泥沙使得高含沙河流具有特殊的產流、匯流、產沙和輸沙規律，會造成河床的劇烈變化。黃河是典型的懸浮泥沙含量較高的河流，也是世界上最復雜、最難治理的河流之一。目前黃河等多沙河流上的泥沙采樣設備大多仍采用傳統的采樣器，部分重要河段只能獲取低量程、低精度的含沙量信息。為了更好地研究黃河流域土壤侵蝕機理和防治水土流失，就必須建立黃河高懸浮含沙量在線實時監測系統。

比較先進的含沙量監測方法有射線法、聲學法、光學法、電容差壓法、浮力法、濁度法、遙感光譜分析法等。這些方法在實際應用中有各自的優勢，但也有各自的局限性。監測含沙量時，傳感器一般是直接插人水體，采集的信號會受到水溫、流速和深度等因素影響。這些影響因素會給監測系統帶來一定的干擾，造成傳感器時間序列信號中存在相應的突變信息，使得測量系統運行失穩。因此，研究含沙量傳感器的線性輸入輸出特性變化并進行含沙量信息多尺度分析具有重要的意義。

小波（wavelet）分析方法是研究水文信息序列多尺度變化特性的有效工具。在含沙量時間序列分析中，同樣可以運用小波的多尺度分析方法，提取含沙量傳感器突變的輸入輸出特性信息?？柭↘al-man）濾波是根據測量數據變化不斷融合的過程，可減少環境因素的干擾。因此，本文提出基于貫序式（sequential）小波多尺度分析和卡爾曼濾波融合的含沙量監測模型，采用音頻共振法來監測黃河含沙量，并同時監測含沙水體的環境信息，進行含沙量數據融合處理，以提高測量系統的精度和穩定性。

1 硬件平臺及試驗數據

1.1 硬件平臺搭建

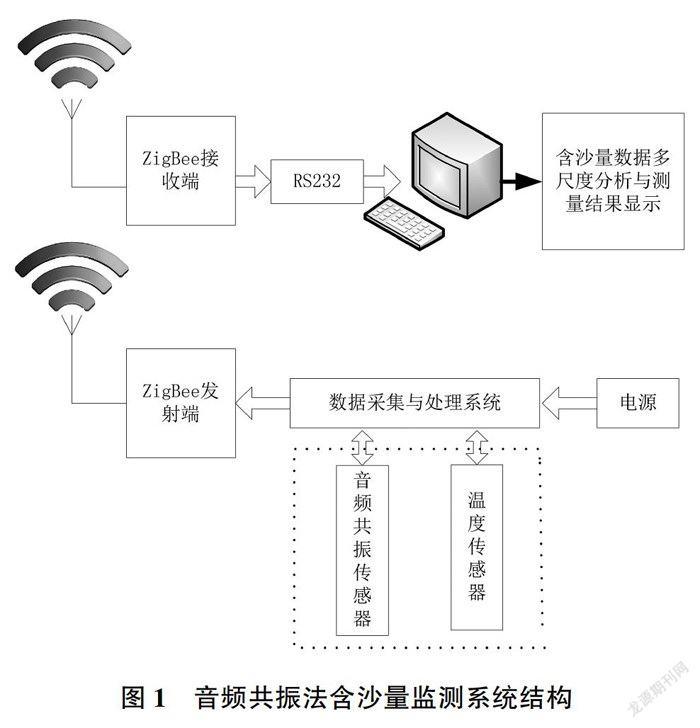
圖1為含沙量監測系統的整體結構。該系統將含沙量、水溫等傳感器集成在一起，可完成多通道信息采集與處理工作。處理后的數據通過ZigBee技術無線傳送給信息處理中心，信息處理中心通過仿真界面實時顯示測量結果。

1.2 試驗材料和試驗數據

試驗材料來源于花園口水文站附近的黃土（含有細沙），同黃河泥沙具有一定的相似性，平均粒徑為176.42μm，中值粒徑為96.56μm。每次試驗都記錄音頻共振傳感器的輸出值K和水溫T，同時用比重瓶獲取含沙量實測值。

從大量試驗數據中經過轉換、濾波、異常值剔除等環節后，本文選取92組數據塊（data block）進行數據融合分析。其中第1組到第46組數據用來擬合，第47組到第92組數據用來驗證。受試驗條件限制，本文只進行了水溫的環境變量監測。

2 多尺度融合模型建立

2.1 諧振頻率的小波分解

音頻共振傳感器的一臂在共振激勵器驅動下作簡諧振動，音頻共振傳感器的另一臂將產生共振，也作簡諧振動。當音頻共振傳感器兩臂浸人到含沙水體時，兩臂間的介質質量發生變化，導致共振頻率發生變化，于是就可通過共振頻率的變化來間接實現含沙量的監測。通過改變振子質量m可改變音叉的共振頻率。設m0為音頻共振傳感器振子的等效質量，mx為水體中含沙量，k為比例因子，則有

由諧振頻率f'（t）便可求出含沙量Mx。

實際應用時，要用傳感器在清水中的固有頻率f0來標定比例因子k。實測時mx不為零，于是通過諧振頻率f（t）就可以建立含沙量監測的反演模型。

小波分析是將信號分解為不同頻率的信號，然后對這些信號進行分析。本文將音頻共振傳感器一段時間內獲取的含沙量數據組成貫序式數據塊進行分析，實現每g個數據組成一個數據塊。任意含沙量時間序列數據塊信號f （t）的離散小波變換（discretewavelet transform，簡稱DWT）系數為

WTf（j，k）==∫Rf（t）ψj，k（t）dt（2）式中：WTf（j，k ）為離散小波變換系數；j、k為小波基數；f為信號的頻率；ψj，k為小波變換核函數；R為實數域；q's.k（ t）為小波變換核函數的歸軛函數。

利用式（2）可以對f（t）進行重構，也就是小波變換的逆變換，其公式為式中：Cψ為對ψ（t）（小波變換核函數的實數域函數）提出的允許性條件；a、b分別為小波尺度；ψ（·）為小小波的位移與尺度伸縮。

2.2 卡爾曼和溫度融合模型

應用動態多尺度系統理論建立基于Kalman濾波的多尺度狀態估計方程，能有效降低測量的均方誤差。但是，一般的Kalman濾波模型僅對狀態方程和測量方程進行融合處理，并沒有考慮環境信息對Kalman濾波模型的融合作用。當不考慮控制信號的作用時，Kalman濾波的估值效果往往不夠理想。此時，傳感器需要進行環境信息的融合處理，以削弱環境因素的影響。一般來說，溫度對傳感器測量過程的影響較大，需要進行溫度補償。傳統的溫度補償方法是通過尋找試驗數據的統計規律來進行軟件補償。本文建立的wavelet-Kalman模型是在進行Kalman估值時直接進行溫度補償。當把溫度信息作為控制信號時，Kalman濾波公式可變為

X（j，k+1）=F（j，k）WTf（J，k）+G（j，k）t（j，k）+

w（j，k）（k≥0）（4）

Z（j，k）=H（j，k）WTf（j，k）（k≥0，j=1，2，…，N）

（5）式中：X（j，k+1）為在某一尺度j上k+1時刻的系統狀態；WTf（J，k）∈Rn×1；F（j，k）為系統矩陣，F（j，k）∈Rn×n；G（j，k）為溫度控制參數；t（j，k）為j尺度下環境溫度控制變量；Z（j，k）為j尺度下k時刻的值；H（j，k）為小波變換的參數矩陣；w（j，k）為噪聲，且滿足式（6）。

E{w（j，k）}=0（k≥0）

E{w（j，k）w（j，l）T}=Q（j，k）δkl（l≥0）（6）式中；E（·）為數學期望值函數；Q（j，K）為非負定對稱陣；δkl為狄拉克函數。

卡爾曼濾波通過無偏估計來達到方差最小，實現卡爾曼最優估計。整個計算流程分為兩部分，一部分是估值的計算流程，另一部分是估值增益的遞推計算流程。具體推導公式可參照卡爾曼最優濾波的5條基本公式。

3 貫序式wavelet-Kalman多尺度融合分析

3.1 基于wavelet的單尺度分析

先用小波函數對音頻共振傳感器的輸出信號進行單尺度分解，設、為音頻共振傳感器輸出的原始信號，cal為小波分解后的低頻系數，cdl為小波分解后的高頻系數。可以看出用單尺度低頻系數cat重構的含沙量信息與傳感器輸出的原始信號波形基本上一致，且低頻系數cat和高頻系數cdl的信號幅值都是原始信號、的一半。

3.2 基于wavelet的多尺度分析

由多尺度分析結果可以看出，尺度3（小波分析的第3層）的低頻系數ca3占整個數據長度的1/4，尺度2的低頻系數cat的長度占整個數據長度的1/4。剩下長度的一半是尺度1的高頻系數cdl。由此可知，低頻系數反映了含沙量信號的輪廓和基本信息，并且各層的系數數量隨著分解層數的增大而減小，原始含沙量數據相應的噪聲得到抑制。因此，可通過對數據進行多尺度變換，提取小波低頻系數來表示含沙量的整體特征，同時利用最小二乘法進行回歸分析，建立不同分解層的反演模型并進行檢驗，確定最佳的小波分解估算模型。

3.3 基于貫序式wavelet-Kalman的多尺度融合分析

小波的分解和重構過程中，若小波分解層數偏小，則低頻子序列仍是含沙量多個時間尺度上信號的混疊，不能很好地消除噪聲；反之，當小波分解層數過大時，會產生虛假含沙量信息，造成含沙量測量誤差累積等問題。目前，小波分析時確定分解層數的常用方法是通過自相關分析對各層小波系數進行白化檢驗，但這種白化自相關分析方法存在分解層數選擇不合理的問題。從表1可以看出，4種小波母函數中，Db8（Daubechies8）、Sym8（Symlets）和Bior6.8（bior-wavf）均是以小波分解的第5層系數構建的模型的均方根誤差扭MSE）最?。?.717 4 _< RMSE <7.6654），穩定性最好，且Sym8小波模型的均方根誤差小于Db8、Coifs（Coiflets）和Bior6.8的。

4 結果與討論

4.1 貫序式wavelet-Kalman多尺度融合結果

分別采用Db8、Sym8，Bior6.8、Coifs共4種小波進行多層離散分解后得到小波低頻系數，并對另外一組數據進行反演，選取均方根誤差作為指標來衡量模型精度。RMSE越大反演模型的精度越低。

貫序式wavelet-Kalman多尺度融合模型選取Sym8小波的ca5層進行小波分解。由于貫序式wavelet-Kalman多尺度融合模型考慮了環境因素的影響，因此輸出結果更接近實測值，反演效果更好，誤差更小，見圖2、圖3。

4.2 貫序式wavelet-Kalman融合誤差比較

為了衡量貫序式wavelet-Kalman多尺度融合模型的效果，給出了多個反演模型的均方根誤差、最大絕對誤差（MaxAE）、平均絕對誤差（MeanAE）和平均相對誤差（MeanRE），見表2。由表2可以看出，貫序式wavelet-Kalman多尺度融合模型的效果最好，其MeanAE為3.95kg/m3，RUSE為3.13kg/m3，MaxAE為14.15kg/m3，MeanRE為1.05kg/m3。表2中的wavelet-Kalman濾波模型是指用Kalman算法進行濾波處理，沒有用Kalman算法進行溫度融合處理，其處理效果較貫序式wavelet-Kalman多尺度融合模型的稍差一些，而Kalman和溫度融合模型的誤差比一元和多元線性回歸模型的小。

從表2還可以看出，經過wavelet多尺度分析和Kalman融合后，音頻共振傳感器的測量誤差都比多元及一元線性回歸的小。整體而言，一元線性回歸的相對誤差較大，但平均相對誤差也在5%以內，可滿足含沙量測量的需要。

一元線性回歸方程是采用前46組數據塊擬合得出的，其表達式為：

y=2.774x+356.3（7）式中：J為含沙量；x為加沙過程中含沙量信息通過音頻共振傳感器轉換的電流值。

多元線性回歸方程為

S=-477.9815+1.4152X1-0.2769X2（8）式中：X1為音頻共振傳感器的輸出信號；X2為溫度傳感器的輸出信息值。

一元線性回歸模型的MeanAE為16.22kg/m3，RUSE為20.18kg/m3，MaxAE為46.90kg/m3。多元融合后的誤差較一元線性回歸的小些，說明考慮不同的環境因素影響，融合效果有提高，但還不是很理想。

5結語

（1）當應用多尺度分析方法提取含沙量信息的突變值并能融合環境因素時，監測誤差相對小，監測精度和穩定性相對高。

（2）貫序式wavelet-Kalman多尺度融合模型能有效提取含沙量的突變信息，同時考慮了環境因素影響，提高了含沙量監測的精度，增強了測量系統的穩定性。

（3）音頻共振法在高懸浮含沙量監測時誤差較小，監測精度較高，表明音頻共振傳感器較適合于高含沙量河流中使用，特別適用于黃河流域的高懸浮含沙量監測。