基于甲型水驅曲線的 體積波及系數變化規律

朱圣舉，張文博，朱 潔

(1.中國石油長慶油田分公司，陜西 西安 710018； 2.低滲透油氣田勘探開發國家工程實驗室，陜西 西安 710018； 3.陜西延長石油(集團)有限責任公司，陜西 延安 716000)

0 引 言

鄂爾多斯盆地北2區水驅砂巖油藏，采用反九點井網注水開發，開采層位為侏羅系延安組延9層，屬低滲透油藏，其水驅規律符合甲型水驅特征曲線，但缺乏相應的水驅體積波及系數變化規律。水驅體積波及系數是指注入水波及到的油藏體積與油藏總體積之比，它是評價水驅油田開發效果的重要參數。求得波及系數的方法有概率論、量綱分析方法、圖像處理技術、實驗方法、經驗公式法、數值模擬法、圖版法[1]、理論分析法[2，3]，或僅對最大水驅波及系數進行評估[4]。然而，以上的研究大都在于求取最終的水驅波及系數，其變化規律仍不甚清楚。部分學者研究了水驅波及系數的變化規律，但是將水驅油效率當作一個定值的處理方法欠妥[5-6]；部分學者將水驅油效率作為變量處理，但是在處理油水相對滲透率比值時，忽視了水驅油效率與含水飽和度成直線關系的限制條件[7]，且以上研究均未涉及到已經廣泛應用的甲型水驅特征曲線。基于此，從甲型水驅特征曲線入手，結合滲流理論，建立了一種新型水驅體積波及系數預測模型。采用鄂爾多斯盆地實際資料對模型進行驗證，同時討論了各參數對自變量(復合變量)的影響及模型的適用條件。

1 模型建立

在油水兩相滲流的條件下，油水兩相相對滲透率之比隨出口端含水飽和度的變化關系在中間階段為[8]：

(1)

式中：Kro、Krw分別為油相、水相相對滲透率；Swe為出口端含水飽和度；c1、d1分別為系數。

水油比為[9]：

(2)

式中：Fw為水油比；Bo、Bw分別為地層原油、地層水的體積系數；μo、μw分別為地層原油、地層水的黏度，mPa·s；ρo、ρw分別為地面原油、地面水的密度，g/cm3。

含水率與水油比的關系為：

(3)

式中：fw為含水率。

將式(1)、(2)代入式(3)，兩邊同時取自然對數后得：

(4)

水驅開發的水驅油效率為：

(5)

平均含水飽和度與出口端含水飽和度的關系為[20]：

(6)

式中：Sor為殘余油飽和度。

將式(6)代入式(5)，得：

(7)

將式(4)代入式(7)，得：

(8)

令

(9)

(10)

則式(8)可改寫為：

(11)

當水驅油藏開發到一定階段時，會出現如下的函數關系式，即甲型水驅特征曲線[10]：

lnWp=B+ANp

(12)

式中：Wp為歷年累計產水量，t；Np為歷年累計產油量，t；A為斜率；B為截距，t。

對式(12)進行求導處理后，可得[11]：

(13)

式中：R為地質儲量采出程度；c為斜率；d為截距。

地質儲量采出程度可以分解為[16]：

R=EDEV

(14)

式中：Ev為水驅體積波及系數。

將式(11)、(13)代入式(14)中，可得：

(15)

將式(15)整理后，得：

(16)

令

(17)

(18)

則式(16)變為：

(19)

式(19)即為水驅體積波及系數隨含水率的變化規律。由于式(1)只在中間階段等式成立，因此，水驅體積波及系數預測公式在含水率達到某一值之后才能使用，這個值根據具體油藏來定。

2 實例分析

鄂爾多斯盆地北2區水驅砂巖低滲透油藏，油層有效厚度為6.3 m，空氣滲透率為48.1×10-3μm2，孔隙度為16.0%，地層原油黏度為2.5 mPa·s，地層水黏度為0.5 mPa·s，地層原油體積系數為1.156，地層水體積系數為1.000，地面原油密度為0.85 g/cm3，地面水密度為1.00 g/cm3，束縛水飽和度為0.30，原始含油飽和度為0.70，殘余油飽和度為0.285。由實驗室巖心分析，其油水相對滲透率比值的自然對數與出口端含水飽和度在中間階段呈直線關系(圖1)：

ln(Kro/Krw)=9.5346-17.918Swe

(20)

式(11)中系數a、b求取方法如下：先根據實驗室得到的相對滲透率數據，由式(3)計算出與不同出口端含水飽和度Swe對應的含水率值fw，由式(7)計算出與不同出口端含水飽和度Swe對應的水驅油效率值ED，再與實際開發油藏的含水率值進行一一對應，最后對出現直線段部分進行線性回歸(圖2)，則：

(21)

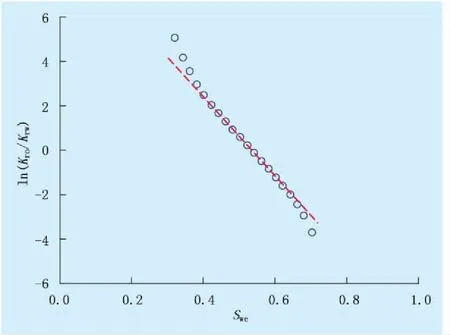
圖1 ln(Kro/Krw)與Swe的關系

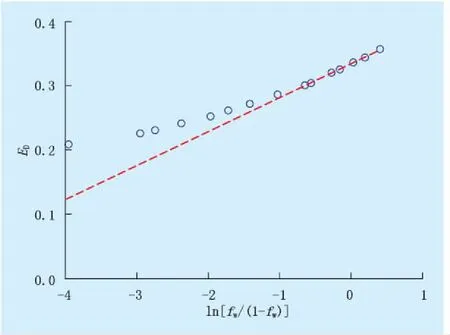
圖2 ED與ln[fw/(1-fw)]的關系

式(13)中系數c、d求取方法如下：由實際油藏開發數據，作地質儲量采出程度R與ln[fw/(1-fw)]關系曲線，對出現的直線段部分進行線性回歸(圖3)，則：

(22)

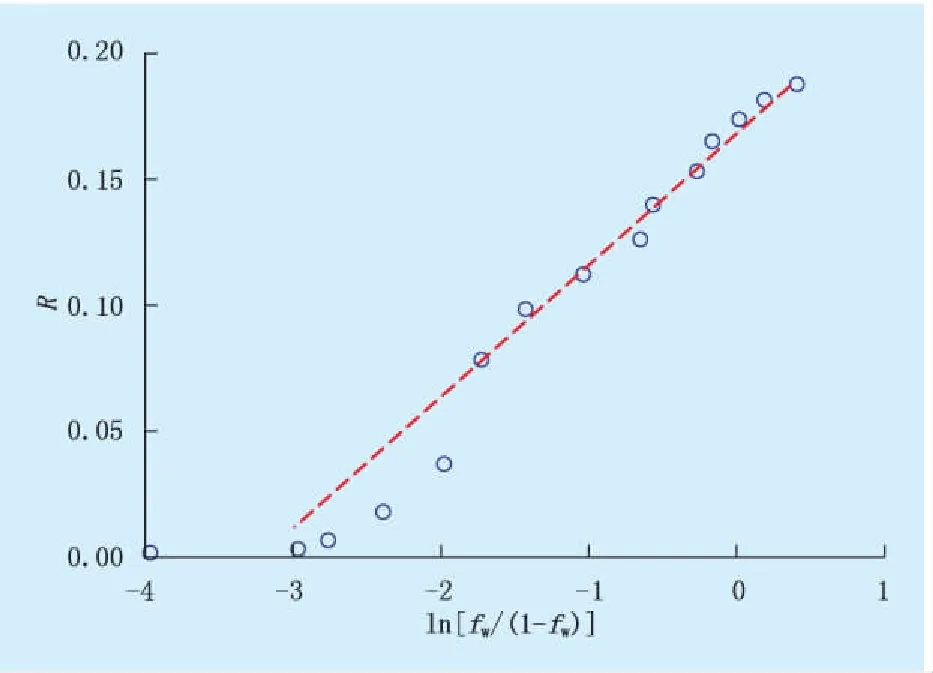
圖3 R與ln[fw/(1-fw)]的關系

式(19)中系數m、n求取方法如下：由實際開發數據計算出不同含水率時的水驅體積波及系數Ev，將a=0.052 8、b=0.334 6代入式(19)中，作Ev與1/{ln[fw/(1-fw)]+b/a} 的關系曲線，對出現的直線段部分進行線性回歸(圖4)，則：

(23)

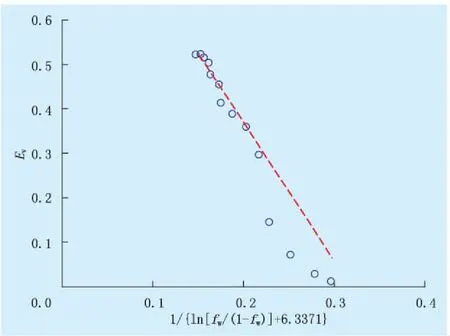
圖4 Ev與1/{ln[fw/(1-fw)]+6.3371}的關系

運用式(23)，即可預測b2q油藏線性關系階段內不同含水率時的水驅體積波及系數。如含水率為60%時，由式(23)計算的水驅體積波及系數為0.403 5；而由動態監測測得的縱向水驅波及系數為0.713 5、平面水驅波及系數為0.575 9，水驅體積波及系數為0.410 9。水驅體積波及系數預測值與實測值的相對誤差僅為1.80%，表明該方法準確性高。

3 討 論

鄂爾多斯盆地北2區水驅砂巖低滲透油藏，在含水率達到40%以后，才能用該模型進行預測，這是由相滲規律所決定的，如圖1所示，ln(Kro/Krw)與Swe只在中間階段呈線性關系。

式(19)中的a、b值作為固定參數參與到自變量1/{ln[fw/(1-fw)]+b/a}中，不會對自變量產生影響，這是由于a、b值主要來源于實驗室巖心測試數據，即a、b值在油藏正式開發之前就已得出。

式(19)不能預測油藏的最終水驅體積波及系數，由圖1可知，油藏在高含水階段的相滲曲線發生了變化，即ln(Kro/Krw)與Swe不再呈線性關系。

4 結論與建議

(1) 基于甲型水驅特征曲線推導出的水驅體積波及系數Ev與由含水率及常數組合而成的復合變量1/{ln[fw/(1-fw)]+b/a}成線性關系，可以用于滿足甲型水驅特征曲線的水驅油藏中間開發階段的水驅體積波及系數評價及預測。

(2) 推導出的水驅體積波及系數預測模型的適用階段，可以由實驗室巖心測試結果確定，模型適用于油水相對滲透率比值的自然對數ln(Kro/Krw)與出口端含水飽和度Swe呈直線關系的階段。

(3) 油藏開發的初期及晚期，由于ln(Kro/Krw)與Swe不呈直線關系，因此，不適于用文中模型來預測水驅體積波及系數，需要探索其他的方法。