CL-20/DNB共晶炸藥晶體缺陷的理論計算

杭貴云，余文力，王 濤，李 臻

(火箭軍工程大學，陜西 西安 710025)

引 言

2,4,6,8,10,12-六硝基-2,4,6,8,10,12-六氮雜異伍茲烷(CL-20)是一種典型的高能量密度含能材料，也是目前綜合性能最好的單質炸藥，具有廣泛的應用價值，但其機械感度高，安全性能差，不能滿足鈍感炸藥的要求，限制了其應用。

近年來，共晶成為一種改善含能材料性能的有效途徑。通過共晶，可以降低含能材料的感度，提高安全性，同時改善其力學性能、氧平衡系數與能量密度。2013年，王玉平等[1-2]以CL-20與1,3-二硝基苯(DNB)為原料，制備了摩爾比為1∶1的CL-20/DNB共晶炸藥，并研究了共晶炸藥的性能。結果表明，CL-20/DNB共晶炸藥的熔點比DNB高44.7℃，感度比CL-20低很多，有望成為一種新型的高能鈍感炸藥。在共晶炸藥制備過程，原料中可能會混入其他成分的雜質，從而導致制備的炸藥樣品中含有雜質。此外，在晶體生長過程中，由于外界因素的干擾，晶體的生長可能會受到影響，使得晶體中存在缺陷，進而影響炸藥的性能，如力學性能、穩定性、感度與爆轟性能等，從而進一步影響武器彈藥的安全性與使用性能[3-5]。因此，研究晶體缺陷對炸藥性能的影響具有重要意義。

本研究分別建立了“完美”型與含有晶體缺陷(摻雜、空位與位錯)的CL-20/DNB共晶炸藥模型，采用分子動力學方法，預測了各種模型的力學性能、結合能、感度與爆轟性能并分析了晶體缺陷對炸藥性能的影響，以期為炸藥性能評估提供參考。

1 計算模型與計算方法

1.1 單個分子模型的建立

CL-20/DNB共晶炸藥由CL-20與DNB組成，在MS軟件中，分別建立CL-20與DNB的單個分子模型，如圖1所示。

1.2 CL-20/DNB共晶炸藥原始模型的建立

CL-20/DNB共晶炸藥屬于正交晶系，空間群為Pbca，晶格參數為a=0.94703nm，b=1.34589nm，c=3.36202nm，α=90.00°，β=90.00°，γ=90.00°，單個晶胞中包含8個CL-20與8個DNB分子[2]。CL-20/DNB共晶炸藥的單個晶胞模型如圖2(a)所示。而后將單個晶胞模型擴展為6(3×2×1)的超晶胞模型，其中包含48個CL-20與48個DNB分子，一共96個分子，如圖2(b)所示。為了便于與含有晶體缺陷的模型進行比較，將“完美”型晶體的模型標記為Model-1。

1.3 CL-20/DNB共晶炸藥缺陷模型的建立

本研究中共包含3種類型的晶體缺陷：摻雜、空位與位錯。

用4個2,4-二硝基甲苯(DNT)分子替換超晶胞模型中的4個DNB分子(圖3(a)中標記為黃色)，得到含4.17%摻雜類型的缺陷晶體模型，標記為Model-2，如圖3(b)所示。

分別用4個1,3,5-三硝基苯(TNB)、4個2,4,6-三硝基甲苯(TNT)、4個六硝基苯(HNB)分子替換圖3(a)中的4個DNB分子，得到缺陷晶體模型，分別標記為Model-3、Model-4與Model-5。

刪除超晶胞模型中最上層的4個CL-20分子(圖4(a)中標記為黃色)，得到含空位為4.17%的缺陷晶體模型，標記為Model-6，如圖4(b)所示。

分別刪除4個DNB、2個CL-20與2個DNB分子，將所得缺陷晶體模型分別標記為Model-7與Model-8。

將“完美”型晶體模型中最上層的CL-20分子向上方移動0.2nm的距離，得到位錯缺陷的晶體模型，標記為Model-9，如圖5所示。

將“完美”型晶體模型中最上層的CL-20分子向下方移動0.2nm的距離，得到缺陷晶體模型，標記為Model-10。

1.4 計算條件設置

分別對CL-20/DNB共晶炸藥的原始模型與含有晶體缺陷的模型進行能量最小化，優化其結構，然后進行分子動力學計算，其中溫度設置為295K，壓力設置為0.0001GPa，選擇NPT系綜與COMPASS力場[6-7]，溫度采用Andersen控溫方法[8]，壓力采用Parrinello控壓方法[9]，范德華力(vdW)的計算采用atom-based方法，靜電作用的計算采用Ewald方法，時間步長為1fs，總模擬步數為2×105步，其中前105步用于熱力學平衡，后105步用于統計分析。模擬過程中，每103fs保存一次軌跡，共得100幀軌跡文件。

2 結果與討論

2.1 平衡判別與平衡體系

在提取數值模擬計算結果時，需要讓混合體系達到熱力學平衡狀態，此時必須同時滿足溫度平衡和能量平衡。通常認為當溫度與能量波動范圍為5%～10%時，體系已經達到平衡狀態。以Model-3為例，混合體系的溫度和能量變化曲線如圖6所示。

從圖6可以看出，模擬初期，溫度與能量均有所上升，并且波動幅度較大。隨著時間的推移，溫度與能量的波動幅度逐漸減小，最終溫度上下波動幅度約為±15K，能量波動幅度也逐漸減小，最終波動幅度在±5%左右，偏差相對較小，表明混合體系已達到熱力學平衡狀態。對于其他類型的晶體模型，分子動力學計算時，均以溫度平衡和能量平衡來判別混合體系是否達到平衡狀態。

2.2 力學性能

力學參數可由彈性系數求得，滿足廣義胡克定律，其表達式為[10-11]：

σi=Cijεj

(1)

式中：σ為應力；ε為應變；Cij(i，j=1，2，…，6)為彈性系數，滿足Cij=Cji，因此獨立的彈性常數只有21個，對于完全的各向同性體，獨立的彈性常數只有2個(C11，C22)。

體積模量(K)與剪切模量(G)的計算公式如下：

KR=[S11+S22+S33+2(S12+S23+S31)]-1

(2)

GR=15[4(S11+S22+S33)-4(S12+S23+S31)+
3(S44+S55+S66)]-1

(3)

式中：下標R表示Reuss平均。柔量系數矩陣S=[Sij]等于彈性系數矩陣C的逆矩陣，即S=C-1。

力學參數之間存在如下關系：

E=2G(1+γ)=3K(1-2γ)

(4)

基于上述公式，可以求得拉伸模量(E)與泊松比(γ)的表達式：

(5)

(6)

當混合體系達到熱力學平衡狀態后，通過分子動力學計算，可以得到不同模型的力學性能參數，結果如表1所示。根據模擬計算結果，可以得到不同模型的力學性能曲線，如圖7所示。

表1 CL-20/DNB共晶的初始模型與缺陷模型的力學性能

從表1與圖7可以看出，“完美”型模型(Model-1)的拉伸模量、體積模量與剪切模量的值最大，分別為14.522、8.811、5.926GPa，而柯西壓的值(0.042GPa)最小，表明炸藥的剛性最強，而延展性較差。由于晶體缺陷的影響，炸藥的晶體結構遭到破壞，因此缺陷晶體的拉伸模量、體積模量與剪切模量減小，表明炸藥的剛性減弱，在外界作用下，炸藥更易發生形變，而柯西壓增大則表明炸藥的塑性與延展性增強。此外，由圖7還可以看出，在缺陷模型中，摻雜缺陷模型(Model-5)對應的拉伸模量、體積模量與剪切模量的值最大，表明力學性能變化最小，而位錯缺陷模型(Model-9)與空位缺陷模型(Model-7)對應的拉伸模量、體積模量與剪切模量減小幅度最大，即剛性減小的幅度最為明顯。因此，位錯缺陷與空位缺陷對炸藥力學性能的影響更為顯著，而摻雜缺陷對力學性能的影響相對較小。

2.3 穩定性

穩定性主要通過結合能(Eb)來體現。結合能越大，說明炸藥中分子之間的相互作用力越強，炸藥的穩定性越好。同時，結合能越大，也說明各組分之間的相容性越好。

結合能的計算公式如下：

Eb=-Einter=-[Etotal-(ECL-20+Eother)]

(7)

式中：Eb為結合能；Einter為分子之間的相互作用能；Etotal為混合體系達到平衡狀態時體系的總能量；ECL-20為去掉體系中的其他組分后，CL-20分子對應的總能量；Eother為去掉CL-20分子后，體系中的DNB與其他組分的總能量。

計算得到不同模型對應的結合能如圖8所示。

從圖8可以看出，在所有模型中，“完美”型模型(Model-1)對應的結合能最大，為336.5kJ/mol，表明CL-20與DNB分子之間的相互作用力最強，炸藥的穩定性最好。在缺陷模型中，摻雜類型的缺陷晶體(Model-3)對應的結合能最大，為305.2kJ/mol，而空位缺陷模型(Model-6、Model-7)對應的結合能最小，分別為278.6、283.1kJ/mol。與“完美”型晶體相比，缺陷模型的結合能減小，減小幅度分別為9.30%、17.21%、15.87%。結合能減小的原因可能是共晶炸藥的晶體結構遭到破壞，導致炸藥分子的排列方式發生變化，分子之間的相互作用強度減弱，從而導致結合能減小，炸藥的穩定性減弱。

2.4 感度

本研究依據“熱點”理論[12]與“引發鍵”思想[13]，選用引發鍵最大鍵長、引發鍵鍵連雙原子作用能和內聚能密度[14-17]為判據，預測炸藥的感度。

2.4.1 引發鍵鍵長

通常認為引發鍵是物質中能量最弱的化學鍵，當受到外界刺激時，引發鍵最容易發生斷裂，從而使炸藥發生分解或爆炸。在CL-20/DNB共晶炸藥及其缺陷晶體中，CL-20的感度最高，對外界的刺激最敏感，最容易發生化學反應，而CL-20的引發鍵為分子中N—NO2基團上的N—N鍵[18-19]，因此選擇N—NO2鍵作為“完美”型晶體與缺陷晶體的引發鍵來預測體系的感度。

以Model-7為例，圖9為經分子動力學模擬后，平衡體系中引發鍵(N—NO2鍵)的鍵長分布情況。

表2給出了不同模型達到熱力學平衡狀態時，混合體系中引發鍵的最可幾鍵長(Lprob)、平均鍵長(Lave)和最大鍵長(Lmax)的變化情況。

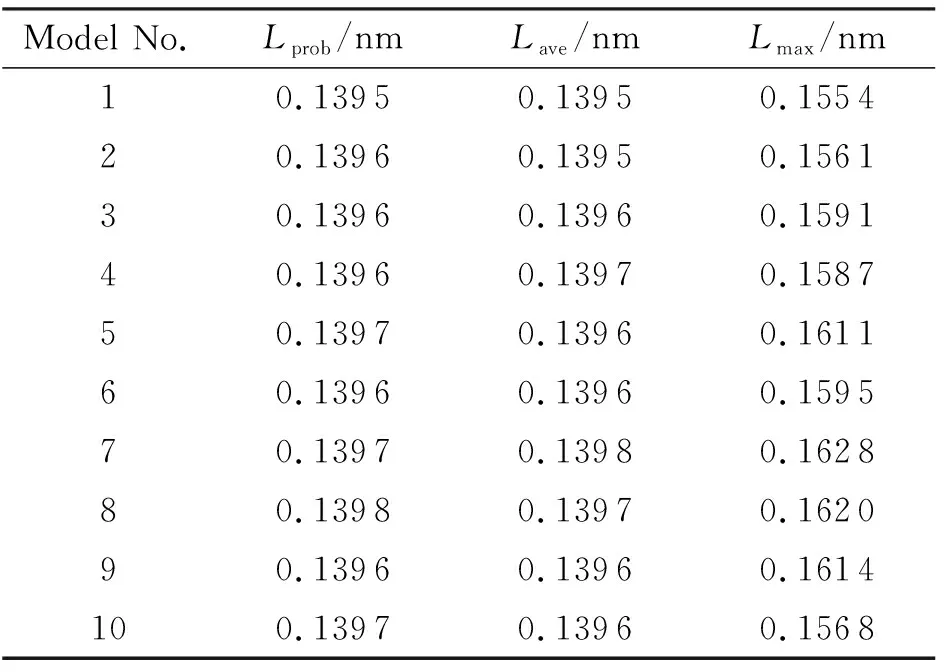
表2 不同模型中引發鍵的鍵長

從圖9可以看出，當混合體系達到平衡狀態時，引發鍵(N—NO2鍵)的鍵長分布呈近似對稱的高斯分布。從表2可以看出，對于不同的模型，最可幾鍵長與平均鍵長近似相等，且變化范圍很小，說明晶體缺陷對最可幾鍵長與平均鍵長的影響很小，而最大鍵長的變化范圍較大。“完美”型晶體模型(Model-1)的最大鍵長最小，為0.1554nm，而缺陷晶體的最大鍵長大于“完美”型晶體模型。其中摻雜缺陷模型(Model-2)的鍵長值最小(0.1561nm)，而空位缺陷模型(Model-7)的鍵長最大(0.1628nm)，最大鍵長的增大幅度為0.45%～4.76%。最大鍵長增大，說明引發鍵的活性增強，炸藥的感度增大，安全性變差。

2.4.2 引發鍵鍵連雙原子作用能

引發鍵鍵連雙原子作用能(EN—N)的計算公式如下：

EN-N=(E1-E2)/n

(8)

式中：E1為混合體系達到熱力學平衡狀態時系統的總能量；E2為固定CL-20中的所有N原子后，混合體系達到平衡狀態時的總能量；n為混合體系中CL-20分子中N—NO2鍵的數目。

不同模型中鍵連雙原子作用能(EN—N)的變化圖如圖10所示。

從圖10可以看出，“完美”型模型(Model-1)的鍵連雙原子作用能最大，為165.74kJ/mol，其次是位錯缺陷模型(Model-10)，為157.28kJ/mol，空位缺陷模型(Model-7)對應的鍵連雙原子作用能最小，為137.23kJ/mol。與“完美”型晶體相比，缺陷晶體模型的鍵連雙原子作用能減小幅度為5.10%～17.20%。鍵連雙原子作用能減小，說明引發鍵的強度減弱，在外界刺激下，引發鍵更容易發生斷裂或者破壞，從而使炸藥發生分解或爆炸。因此，“完美”型晶體的感度最低，安全性最好，而缺陷模型的感度升高，安全性變差。

2.4.3 內聚能密度

內聚能密度(CED)等于范德華力與靜電力之和，即分子的非鍵力。通過分子動力學模擬，得到不同模型的內聚能密度與相關能量，結果見表3。

表3 不同模型的內聚能密度與相關能量

從表3可以看出，“完美”型模型的內聚能密度、范德華力與靜電力的值最大，分別為0.897、0.257和0.640kJ/cm3，而缺陷模型的內聚能密度、范德華力與靜電力均小于“完美”型模型對應的能量值。在缺陷模型中，CED的最大值與最小值分別為0.875和0.774kJ/cm3。與“完美”型晶體相比，CED減小的幅度為2.45%～13.71%。內聚能密度減小，說明炸藥的感度增大，安全性變差，因此晶體缺陷使得炸藥的感度增大，其中位錯缺陷模型對應的CED值最小，表明其感度最高。

2.5 爆轟性能

采用修正氮當量法[20]計算炸藥的爆轟參數并對其能量特性進行預測。

對于由C-H-O-N 4種元素組成、化學式為CaHbOcNd的炸藥，氧平衡系數(OB)計算公式為：

(9)

式中：a、b、c分別為炸藥分子中包含的C、H與O原子的數目；Mr為炸藥的摩爾質量，g/mol。

對于混合炸藥，氧平衡系數的計算公式如下：

OB=∑wiOBi

(10)

式中：wi為混合炸藥中第i種組分所占的質量分數(%)；OBi為第i種組分對應的氧平衡系數。

根據修正氮當量理論，爆轟參數(D、P)的計算公式如下：

(11)

式中：D為爆速，m/s；p為爆壓，GPa；ρ為炸藥的密度，g/cm3；∑Nch為炸藥的修正氮當量；pi為1mol炸藥爆炸時生成第i種爆轟產物的摩爾數；Npi為第i種爆轟產物的氮當量系數；BK為炸藥分子中第K種化學鍵出現的次數；NBK為炸藥分子中第K種化學鍵的氮當量系數；Gj為炸藥分子中第j種基團出現的次數；NGj為炸藥分子中第j種基團的氮當量系數。

根據修正氮當量法，通過計算得到不同模型的爆轟參數，結果如表4所示，其中炸藥的密度可以直接從分子動力學結果中提取得到。

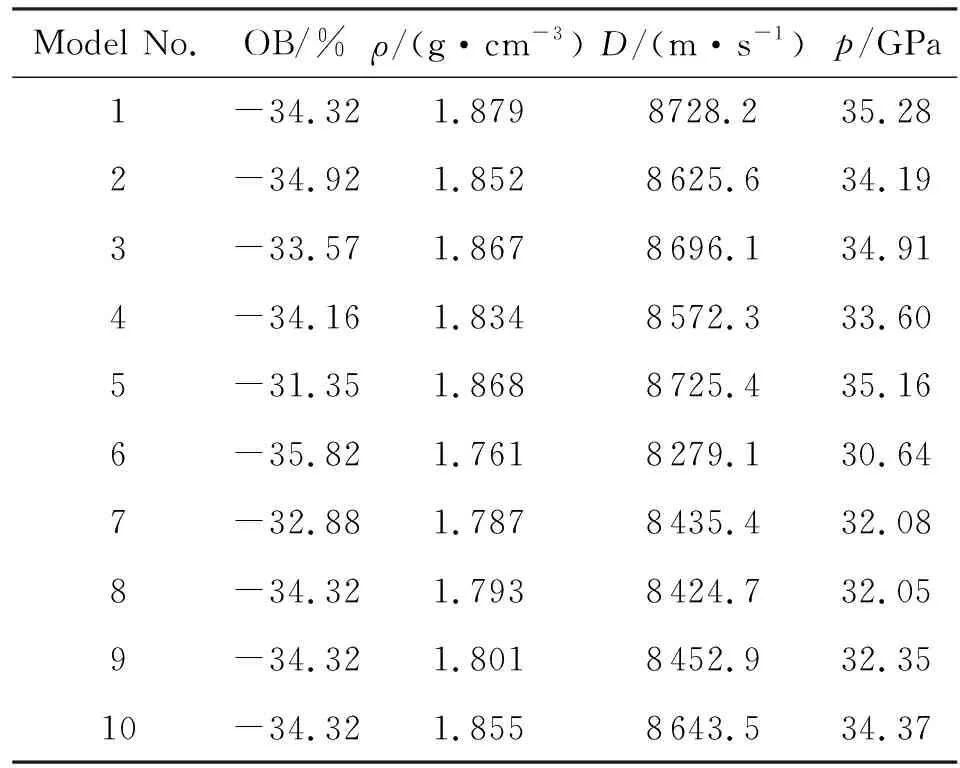
表4 不同模型的爆轟參數

從表4可以看出，“完美”型模型(Model-1)的密度、爆速、爆壓最大，而缺陷晶體的密度與爆轟參數均有所減小。在缺陷模型中，摻雜缺陷模型(Model-5)對應的密度、爆速、爆壓最大，而空位缺陷模型(Model-6)對應的密度、爆速、爆壓最小。與“完美”型模型相比，缺陷晶體(Model-6)的密度、爆速、爆壓減小幅度分別為6.28%、5.15%、13.15%。密度與爆轟參數減小，說明炸藥的能量密度減弱，威力減小。因此，可以看出晶體缺陷使得炸藥的能量密度降低，其中空位缺陷的模型能量密度最低，即空位缺陷對炸藥能量密度的影響最大。

3 結 論

(1)與“完美”型晶體相比，缺陷晶體模型的拉伸模量、體積模量與剪切模量的值減小，而柯西壓增大，表明由于晶體缺陷的影響，炸藥的剛性減弱，延展性增強，其中空位缺陷與位錯缺陷對力學性能的影響更為顯著，而摻雜缺陷的影響相對較小。

(2)由于晶體缺陷的影響，炸藥的晶體結構與分子排列方式發生變化，導致分子之間的相互作用力減弱，結合能減小，炸藥的穩定性減弱。

(3)缺陷晶體的引發鍵鍵長增大，而鍵連雙原子作用能與內聚能密度減小，表明炸藥的感度增大，安全性減弱。

(4)由于晶體缺陷的影響，炸藥的密度與爆轟參數減小，表明炸藥的威力減小，能量特性受到削弱，其中空位缺陷的晶體密度與爆轟參數最小，即空位缺陷對能量特性的影響最大。