對“聯(lián)動問題”的解法探究
——用“微元法”和“轉(zhuǎn)換參考系法”雙解“聯(lián)動問題”

孫德峰

(北京第十二中學(xué) 北京 100071)

劉 芳

(北京教育學(xué)院豐臺分院 北京 100073)

在不少的競賽題目中，都涉及到了“聯(lián)動問題”．一般來講，這些待求解的運(yùn)動形式都較為復(fù)雜，利用高中教材中所講授的典型運(yùn)動規(guī)律很難求解，因此大部分輔導(dǎo)資料都采用了“微元法”來求解．

用“微元法”固然能夠?qū)栴}解決，而且有利于提高學(xué)生解決動態(tài)變化過程的能力，但“微元法”也存在解題過程相對繁瑣的不足．筆者在教學(xué)過程中發(fā)現(xiàn)，在解決“連結(jié)體”間的運(yùn)動學(xué)問題時，由于涉及到的是兩個或兩個以上物體之間的運(yùn)動，故靈活地轉(zhuǎn)換參考系，會使問題大大得到簡化．下面甄選4個典型題目，各用兩種方法求解，供讀者參考．

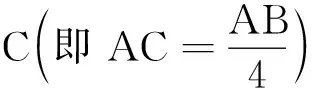
圖1 例1題圖

微元法:

從如圖1所示的時刻再經(jīng)過Δt→ 0的時間，圓環(huán)運(yùn)動到了如圖2所示的虛線位置．為了讀者閱讀方便，筆者將圓環(huán)的移動距離做了適當(dāng)?shù)目鋸?以下皆為如此)．容易發(fā)現(xiàn)圓環(huán)與直桿的交點(diǎn)M點(diǎn)運(yùn)動到了M′點(diǎn)，連接OM和O′M′，交點(diǎn)為D．由于Δt→ 0，不難得到

∠MDM′ = ∠ODO′ = Δθ→ 0

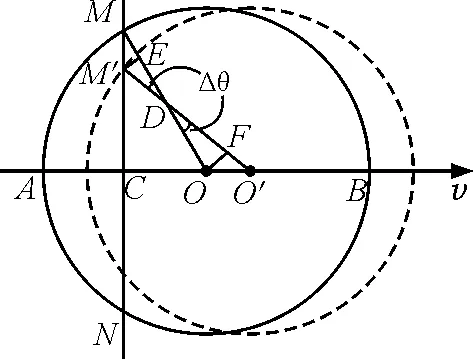
圖2 圓環(huán)移動

在OM上取一點(diǎn)E，使得DE=DM′；在DO′上取一點(diǎn)F，使得DO=DF．

值得注意的是，我們現(xiàn)在構(gòu)造了兩個非常特殊的等腰三角形．由于頂角趨近于零，則兩個底角就趨近于90°，可以認(rèn)為底邊與兩腰近似垂直．不妨給這樣的三角形起一個特殊的名字——“雙直角等腰三角形”．在接下來的題目中我們會逐漸體會到這種特殊的三角形在“微元法”中所起到的作用．

由于OM=O′M′，所以ME=O′F．因?yàn)镃點(diǎn)是4等分點(diǎn)，則∠CMO= 30°；∠COM= 60°．再根據(jù)OM⊥OF,可知：∠FOO′ = 30°．所以MM′cos30° =ME=O′F=OO′sin30°，又OO′ =vΔt；MM′ =vMΔt，代入上式可得

轉(zhuǎn)換參考系法：

由于直桿沒動，所以沿直桿方向的速度即為M點(diǎn)相對地面的速度．以圓環(huán)為參考系，因?yàn)镸點(diǎn)同時又沿圓環(huán)運(yùn)動，故M點(diǎn)相對圓環(huán)的速度必沿圓環(huán)切線方向；同時，圓環(huán)又水平向右運(yùn)動，所以圓環(huán)的速度v又可理解為牽連速度．根據(jù)v絕對=v相對+v牽連可知三者速度的幾何關(guān)系如圖3所示．很容易看出

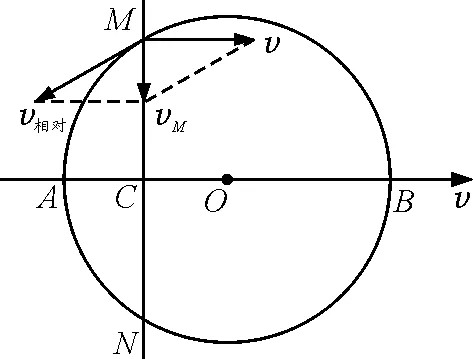
圖3 絕對速度、相對速度、牽連速度幾何關(guān)系

【例2】如圖4所示，一個半徑為R的環(huán)(環(huán)心為O2)立在水平面上，另一個同樣大小的環(huán)(環(huán)心為O1)以水平向右的速度v從前一個環(huán)的旁邊經(jīng)過．試求當(dāng)兩環(huán)環(huán)心相距為d(2R>d> 0)時，兩環(huán)上部的交點(diǎn)A的運(yùn)動速度．兩環(huán)均很薄，可以認(rèn)為兩環(huán)是在同一個平面內(nèi)，第二個環(huán)是緊貼著第一個環(huán)掠過去的．

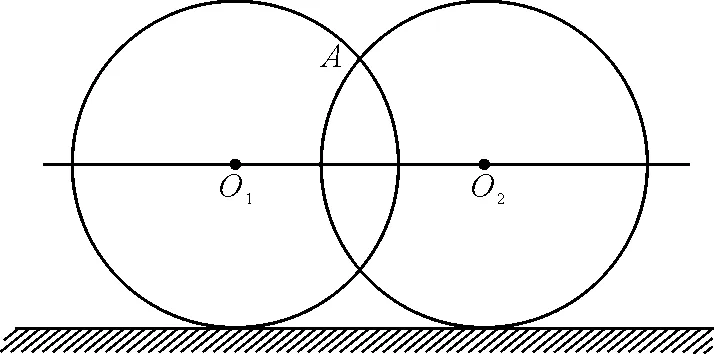
圖4 例2題圖

微元法：

從如圖4所示的時刻再經(jīng)過Δt→ 0的時間，圓環(huán)運(yùn)動到了如圖5所示的虛線位置．交點(diǎn)由A點(diǎn)運(yùn)動到了B點(diǎn)，而原來的A點(diǎn)隨左邊圓環(huán)平移到了C點(diǎn)．由于Δθ→0，所以△ABO2為“雙直角等腰三角形”，故

∠CAB= 90°-θ

圖5 圓環(huán)運(yùn)動

又知道AC=O1O1′，所以有

轉(zhuǎn)換參考系:

仿照例1的做法，不妨以運(yùn)動的圓環(huán)為參考系，絕對速度為交點(diǎn)沿靜止圓環(huán)運(yùn)動的速度；相對速度為沿運(yùn)動圓環(huán)運(yùn)動的速度；牽連速度為運(yùn)動圓環(huán)自身的速度，如圖6所示．

圖6 速度關(guān)系

根據(jù)幾何圖形的對稱性，交點(diǎn)A沿兩圓環(huán)的運(yùn)動速度大小必然是相等的，圖6中的矢量三角形為等腰三角形，故根據(jù)幾何關(guān)系可得

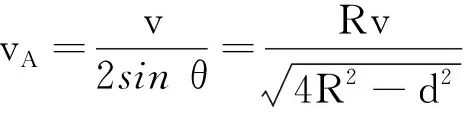
【例3】兩只小環(huán)O和O′分別套在靜止不動的豎直桿AB和A′B′上．一根不可伸長的繩子，一端系在A′點(diǎn)上，繩子穿過環(huán)O′，另一端系在環(huán)O上．如圖7所示，若圓環(huán)O′以恒定速度v′沿桿向下運(yùn)動，∠AOO′ =α?xí)r，求圓環(huán)O的運(yùn)動速度為多大？

圖7 例3題圖

微元法：

從如圖7所示的時刻再經(jīng)過Δt→ 0的時間，兩圓環(huán)及細(xì)線運(yùn)動到了如圖8所示的虛線位置．在OE上取一點(diǎn)D，使CE=DE；在O′E上取一點(diǎn)D′，使C′E=D′E．由于Δt→0，故Δθ→0，所以又構(gòu)造了兩個“兩直角等腰三角形”．

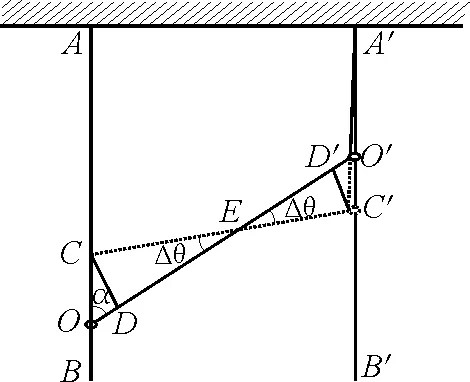
圖8 圓環(huán)及細(xì)線運(yùn)動

根據(jù)繩長不會發(fā)生變化這一特點(diǎn)，可寫出幾何關(guān)系

OO′ =O′C′ +CC′

結(jié)合上述特殊三角形的構(gòu)造，得到

OD+O′D′ =O′C′

考慮到運(yùn)動情況

OD=OCcosα=vΔtcosα

O′D′=O′C′cosα=v′Δtcosα

結(jié)合式(3)可以得到

轉(zhuǎn)換參考系法：

本題有別于以上兩個例題，連結(jié)體的兩個“主角”都在運(yùn)動，在這種情況下，就更需要以其中一個運(yùn)動物體為參考系而不是以地面為參考系，從而使問題得到簡化．例如，本題可以以O(shè)′環(huán)為參考系，則容易得到O環(huán)相對O′環(huán)的速度為

v相對=v+v′

在假定O′環(huán)不動的前提下，本題就簡化為繩子末端速度分解的問題，如圖9所示，沿繩子和垂直于繩子將v相對分解，得到

v相對cosα=(v+v′)cosα

圖9 繩子末端速度分解

其中“v相對cosα”可以理解為收繩子的速度，即圓環(huán)O′下滑的速度v′，從而得到

v′=(v+v′)cosα

即

【例4】如圖10所示，A，B，C為3位芭蕾舞演員同時從邊長為l的三角形頂點(diǎn)A，B，C出發(fā)，以相同的速率v運(yùn)動；運(yùn)動中始終保持A朝著B，B朝著C，C朝著A．試問經(jīng)過多少時間3人相聚？每個演員跑了多少路程？

圖10 例4題圖

微元法：

本題很明顯是一個連續(xù)變化的問題，首先想到的是利用“微元法”來解決．從如圖10所示的時刻再經(jīng)過Δt→ 0的時間，3位演員及其連線運(yùn)動到了如圖11所示的長虛線位置；又經(jīng)過Δt→ 0的時間，3位演員及其連線運(yùn)動到了短虛線的位置……

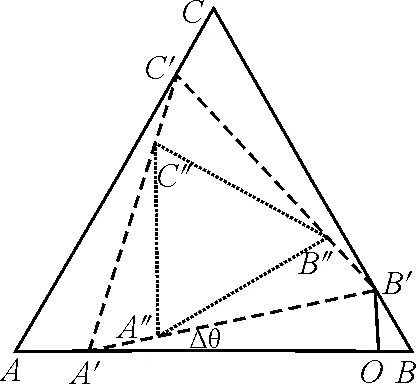
圖11 3位演員及連線運(yùn)動的情況

由于Δt→0，故Δθ→0，在A′B上截取A′O=A′B′，又構(gòu)造了一個“兩直角等腰三角形”．所以

A′B′=A′O=AB-AA′-OB

其中

AA′=vΔt

聯(lián)立以上3式可得

同理

最終3位演員會相聚到一點(diǎn)，故

AnBn=0

得到

每位演員跑過的路程

轉(zhuǎn)換參考系法：

A，B，C運(yùn)動形式相同，故只需關(guān)注A，B就可以將問題解決．不妨以B演員為參考系，經(jīng)過分析可以知道：A，B始終在一條直線上；A與B速度方向的夾角始終為120°．

那么A，B兩位演員沿二者連線方向上彼此接近的相對速度為

最終A，B相遇，則A相對B走過的距離為l，則

故有

從以上4個例題來看，“微元法”的解題套路都很相似——構(gòu)造好“兩直角等腰三角形”，確立好邊長和運(yùn)動的關(guān)系即可將問題解決．“微元法”的優(yōu)點(diǎn)是思路簡單、易操作；缺點(diǎn)是畫圖、運(yùn)算過程相對較為復(fù)雜．

而“轉(zhuǎn)換參考系法”則是建立在對物體間運(yùn)動關(guān)系的準(zhǔn)確把握之上，當(dāng)一個物體運(yùn)動，另一物體相對地面保持靜止的時候(例1和例2)，我們往往以運(yùn)動物體為參考系，利用相對運(yùn)動的矢量方程即可；在兩個或兩個以上物體都運(yùn)動的時候，不能簡單、直接地套用相對運(yùn)動矢量方程得到相對速度，而是應(yīng)該仔細(xì)觀察二者之間的運(yùn)動關(guān)系，究竟是合成之后再分解(例3)，還是分解之后再合成(例4)，這要視題目而定．

方法無好壞之分，從培養(yǎng)學(xué)生物理思維和解題能力的角度來講，這兩種解題思路都值得向?qū)W生介紹，只有這樣，學(xué)生在遇到問題時才能有更開闊的思路，甚至還會想出更精彩的解法．