基于極限學習機模型的 中國西北地區參考作物蒸散量預報

魏 俊，崔寧博,2，陳雨霖，張青雯，馮 禹,3，龔道枝，王明田

(1.四川大學水力學與山區河流開發保護國家重點實驗室，四川 成都 610065； 2. 南方丘區節水農業研究四川省重點實驗室， 四川 成都 610066； 3. 西北農林科技大學旱區農業水土工程教育部重點實驗室，陜西 楊凌 712100；4.中國農業科學院農業環境與 可持續發展研究所作物高效用水與抗災減損國家工程實驗室，北京 100081； 5. 四川省農業氣象中心，四川 成都 610071)

0 引 言

參考作物蒸散量(ET0)是反映大氣蒸散能力，科學評價區域干旱程度及植被耗水量的重要指標[1,2]。ET0的精確計算對于作物需水量的預測、區域農業用水優化調控以及區域水資源管理的嚴格落實具有重大意義[3]。目前，科學家提出的ET0計算方法大致可分為溫度法、輻射法、綜合法等[4,5]。其中溫度法有Hargreaves-Samani[6]、Thomthwaite、Mccloud[7]等模型，輻射法有FAO-24Radiation、Priestley-Taylor[8]、 Makkink[9]、Priestly-Taylor等模型[ 0]，綜合法有Penman-Van Bavel[11]、1948-Penman[12]等模型。

隨著現代計算機和信息技術的不斷發展，國內外研究人員相繼提出了不同的基于機器學習ET0模擬預報模型[13-15]。SHIRI等[16]將基因表達式編程算法用于ET0模擬，其模擬精度優于Priestly-Taylor、Hargreaves-Samani等模型。劉麗[17]等利用人工神經網絡對GM(1，1)模型殘差系列進行修正，并構建組合模型，在鞍山地區的ET0預報中取得較高精度。極限學習機(extreme learning machine，ELM)相較于其他的機器學習模型具有精度高、學習快等優點[18]。目前已被應用于圍巖穩定性預測[19]、暴流風速預測[20]、鑄件晶粒尺寸預測[21]等領域。

本文擬將Penman-Monteith[4](P-M)模型計算的ET0作為標準值，構建ELM的ET0預報模型，并用K-折交叉驗證估計泛化誤差，與其他在西北地區精度較高的ET0計算模型進行比較，提出在缺乏氣象資料的情況下的最優計算模型，為該區域水資源優化調配及精準灌溉預報提供科學依據。

1 材料與方法

1.1 研究區域概況

中國西北地區深居亞洲內陸，干旱是制約當地發展的主要因素之一。據統計，在現有水資源條件下，如果要滿足現有國民經濟需水，西北諸河缺口達3.7×109m3[22]。本文選用敦煌、額濟納旗、喀什、烏魯木齊、銀川和格爾木等6個代表性國家氣象站點數據，構建基于k-折交叉驗證估計泛化誤差的ELM 模型進行ET0預報。將1993-2016年逐日氣象數據分為18組，其中17組為訓練樣本，1組為模擬樣本，包括最高氣溫(Tmax)、最低氣溫(Tmin)、日照時數(n)、相對濕度(RH)距地面2 m高處的風速(u2將10 m高處的風速利用FAO風廓線關系[4]換算成2 m高處的風速)。

1.2 參考作物蒸散量計算模型

P-M模型是基于的空氣動力學和能量平衡原理建立的，具有明確的物理意義。該模型考慮了ET0的各種影響因子，不需要因局地氣候差異而進行參數修正。其計算結果與全球氣象站實測數據十分相近，具有普遍的適用性[23-24]，因此本文選用P-M模型計算的ET0作為標準值。為檢驗ELM模型預報精度，選用Hargreaves-Samani、Chen、EI-Sebail和Bristow[25]等4種在西北地區ET0計算精度較高的模型與ELM模型進行比較，具體模型及計算公式見表1。

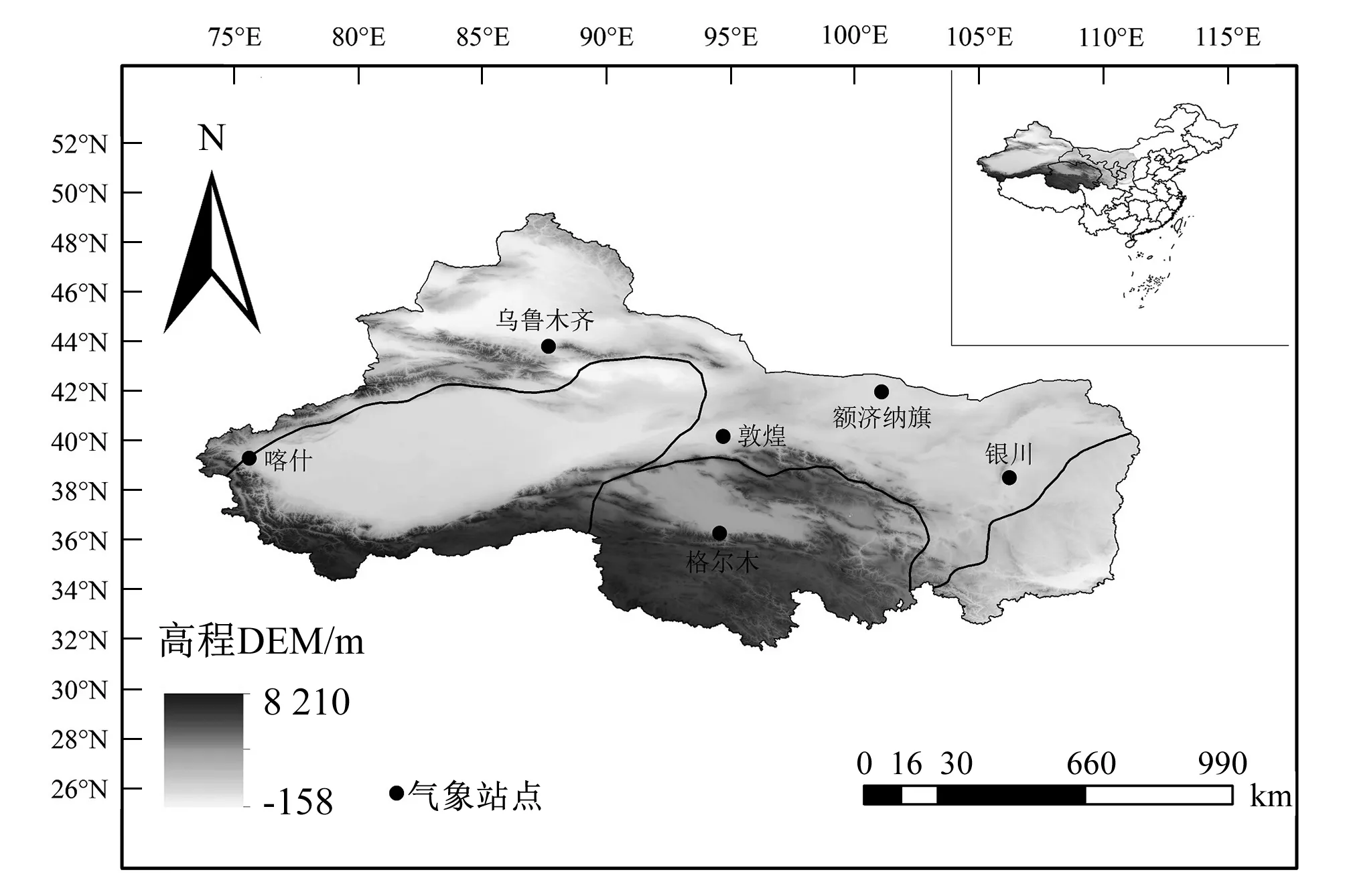
圖1 站點分布圖Fig.1 Distribution of meteorological station

1.3 極限學習機(ELM)計算原理

ELM是一種針對單層前向神經網絡(single layer forward neural network，SLFN)的新算法，該算法隨機產生輸入層與隱含層間的連接權值及隱含層神經元的閾值，且在訓練過程中無需調整，只需要設置隱含層神經元個數，便可獲得唯一最優解。與傳統的訓練方法相比，該方法學習具有速度快、泛化性能好等優點。其網絡拓結構見圖2，其具體實現方法參見文獻[26]。

1.3.1 K-折交叉驗證原理

泛化誤差(generalization error，GE)是在獨立測試樣本上的期望預報誤差，也被稱為測試誤差(test error，TE)或預報誤差(prediction error，PE)，主要用于定量描述模型的性能[27,28]。由于在實際應用中很難確定樣本的分布，導致不能準確得出泛化誤差，通常用樣本的訓練誤差替代泛化誤差，但是這種近似替 代具有很強的隨機性，不能準確地評價模型的優劣，所以一些通過樣本重新估計泛化誤差的方法被提出。本文主要利用K-折交叉驗證法估計泛化誤差，具體實現方法見文獻[28]。

表1 參考作物蒸散量計算模型Tab.1 Calculation model of reference crop evapotranspiration

注：ET0為參考作物蒸散量，mm/d；Rn為凈輻射，MJ/(mm2·d)；T為平均氣溫，℃；u2為距地面2 m高處的風速，m/s；es為飽和水汽壓，kPa；ea為實際水汽壓，kPa；Δ為飽和水汽壓-溫度曲線斜率，kPa/℃；γ為濕度計常數，kPa/℃；Ra為大氣頂層輻射，MJ/(mm2·d)；下同。

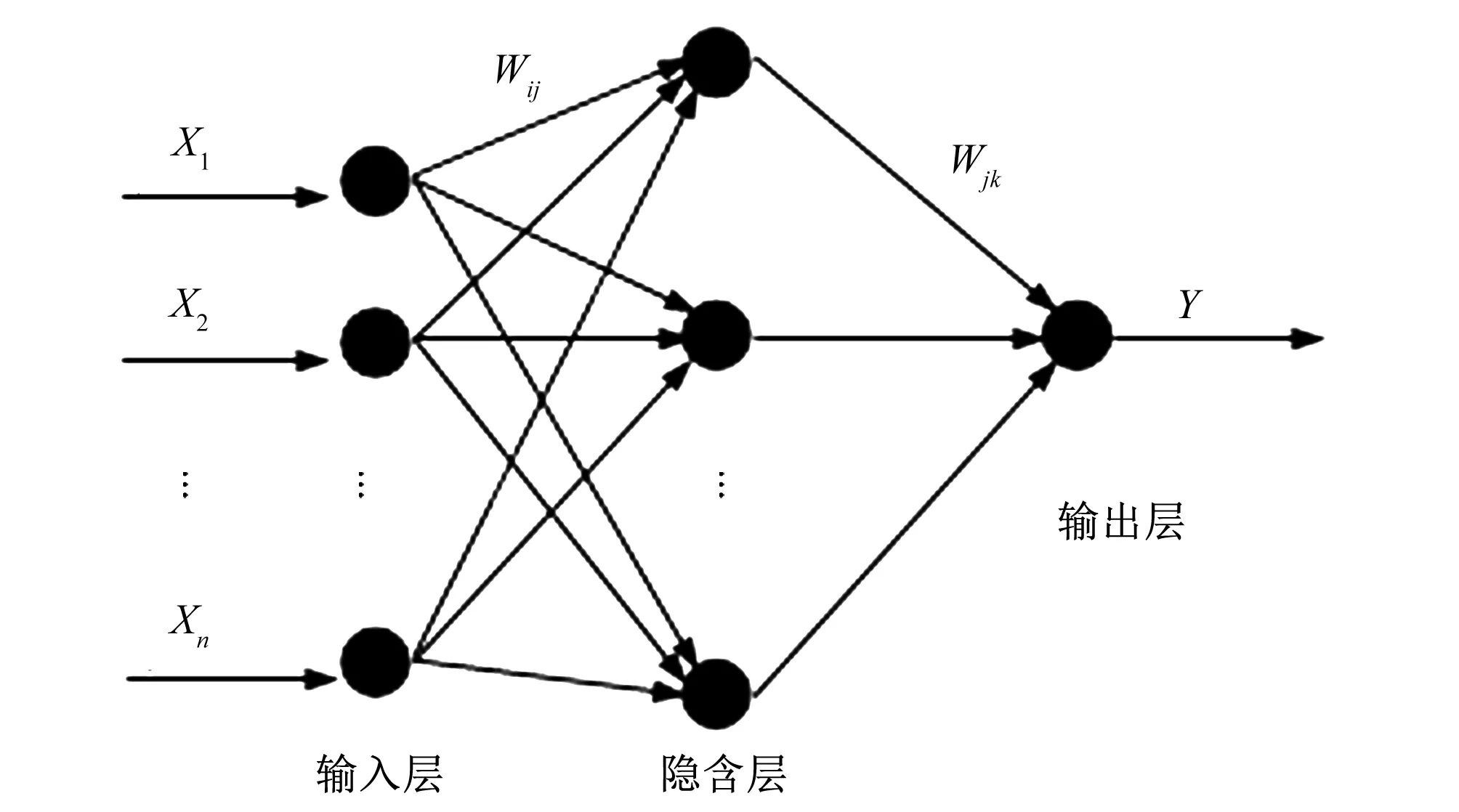
圖2 極限學習機拓撲結構Fig.2 Topological structure of extreme leaning mechane

1.4 模型驗證

本文選用平均絕對誤差(MAE)、均方根誤差(RMSE)、納什系數(NSE)和決定系數(R2)和，并將其統一到整體評價指標[29](global Performance Indicator，GPI)評價模型的精度，具體公式如下：

(1)

(2)

(3)

(4)

(5)

2 結 果

2.1 不同氣象資料輸入情況下ELM模型的模擬精度

將不同氣象因子隨機組合，構成不同的輸入情況，建立對應的ELM模型，結果見表2。

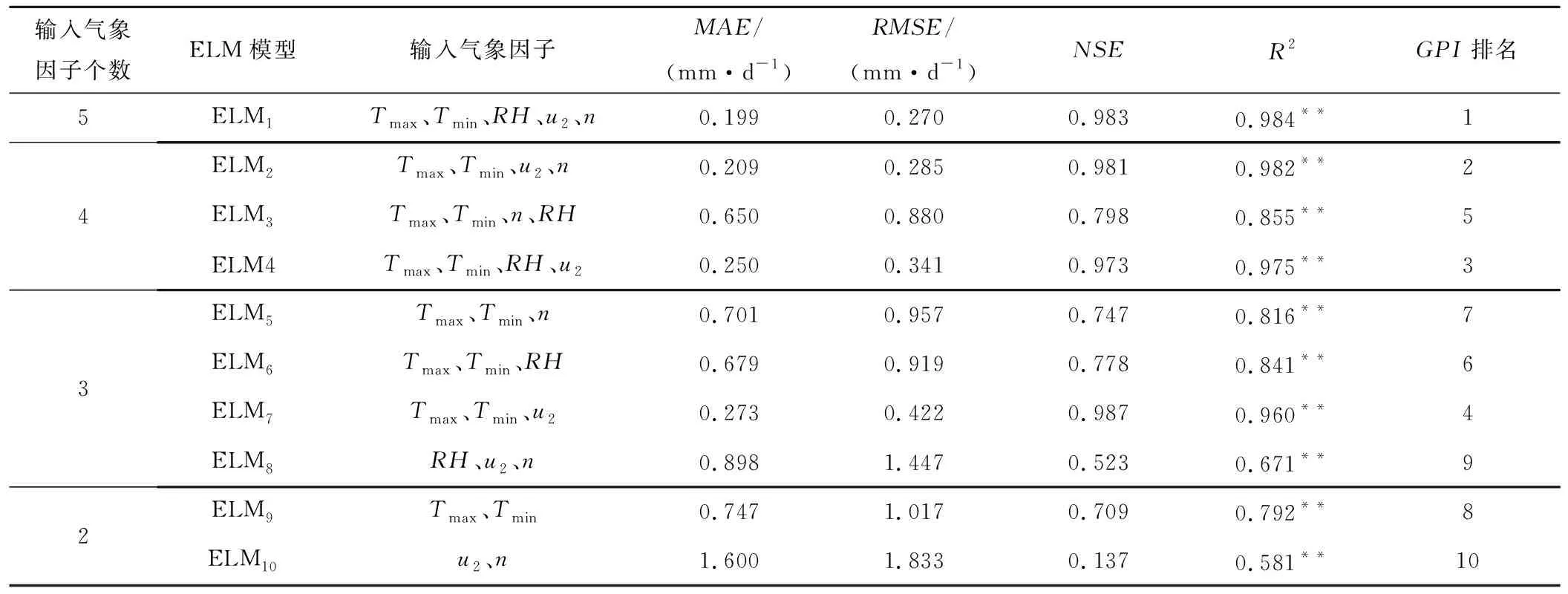
表2 不同氣象因子輸入下ELM參考作物蒸散量模擬精度Tab.2 Reference crop evapotranspiration simulation accuracy of ELM with different meteorological factors

注：**表示在1%的水平上極顯著相關，ELM1、ELM2…ELM10表示不同氣象因子輸入情況下的ELM模型，下同。

輸入5個氣象因子時，ELM1的MAE為0.199 ，RMSE為0.270 mm/d，NSE、R2分別為0.983、0.984，GPI排名第1。該結果表明ELM1在氣象資料齊全時，能夠精確地表示氣象因子和ET0之間的非線性關系，模型精度較高。

輸入4個氣象因子時，ELM3(缺少u2)和ELM2(缺少RH)、ELM4(缺少n)的模擬精度具有明顯差異。ELM2的NSE、R2均在0.98以上，ELM4的NSE、R2均在0.97以上，ELM3的NSE、R2僅有0.798、0.855，ELM3的MAE、RMSE比ELM4高出160%、158%，比ELM2高出211%、208%，ELM2、 ELM3、ELM4的GPI排名分別是2、5、3，結果表明ELM2、ELM4的模擬精度高于ELM3。對比ELM1和 ELM3，發現在缺少u2時，模型的模擬精度大幅下降，MAE從0.199 mm/d上升到0.650 mm/d，RMSE從0.270 mm/d上升到0.880 mm/d，NSE下降了18.81%，R2下降了13.11%，表明u2對西北地區ET0影響較大，該結果與汪彪[30]、謝賢群[31]等人結論一致。

輸入3個氣象因子時，ELM5(缺少RH、u2)、ELM6(缺少u2、n)、ELM7(缺少RH、n)和ELM8(缺少Tmax、Tmin)模擬精度差異顯著，GPI排名分別為7、6、4、9。其中ELM7的MAE、RMSE、NSE和R2分別是0.273 、0.422 、0.987和0.960、上述指標均優于其他3個模型的對應指標。對比ELM3和ELM5，發現減少RH后，MAE從0.650 mm/d上升到0.701 mm/d，NSE下降了6.39%，GPI排名從第5下降到第7，模擬精度小幅下降。該結果和馮禹[3]、侯志強[13]等研究結果略有差異，他們研究認為在減少氣象因子RH后，模型的模擬精度反而上升。因此，在僅有Tmax、Tmin和u2時，ELM7可作為西北地區ET0模擬的推薦模型。

輸入2個氣象因子時，ELM9(輸入Tmax、Tmin)和ELM10(輸入u2、n)的GPI排名分別為8、10。ELM9在僅輸入溫度時的高達NSE、R2分別為0.709、0.792，相較于ELM5、 ELM6模型，少了n、RH等氣象因子，對應的指標僅略微下降，說明氣溫是西北地區ET0的核心驅動因子。

2.2 ELM模型可移植性分析

在西北地區ELM1、ELM2、ELM4和ELM7等4模型模擬ET0精度較高，為了探究在ELM模型的可移植性，隨機選擇訓練站點P和測試站點T站點的數據組合，形成5組測試集和訓練集樣本，構建模型，其模擬結果如表3所示。ELM1、ELM2、ELM4和ELM7等4種模型除了ELM7在喀什和敦煌間進行訓練模擬的精度相對較低，其余模型在不同站點間的模擬精度很高，MAE、RMSE分別在0.40、0.52 mm/d以下，NSE、R2分別在0.95、0.96以上。結果表明在站點氣象資料缺乏情況下，不同站點間ET0模擬能取得較高精度，為ET0計算提供了一種新的思路。

2.3 ELM模型與其他模型模擬精度比較

在常用的ET0計算模型中篩選了4種在西北地區精度較高的模型，其分別是Hargreaves-Samani、Chen、EI-Sebail和Bristow，具體計算公式見表1。以P-M模型計算結果為標準值，比較在相同輸入情況下EI-Sebail、Hargreaves-Samani、Chen和Bristow和ELM6、ELM9的模擬精度，具體結果見表4。

表4中的數據表明，無論是基于Tmax、Tmin、RH構建的ELM6還是基于Tmax、Tmin構建的ELM9，其模擬精度均高于在相 同輸入情況下的其他模型。在輸入Tmax、Tmin、RH時，ELM6的MAE、RMSE分別是0.679 和0.919 mm/d， EI-Sebail的MAE、RMSE分別是0.726 、0.989 mm/d，且ELM6的NSE和R2均高于EI-Sebail的對應指標，說明ELM6的模擬精度高于EI-Sebail模型。在輸入Tmax、Tmin時ELM9的4項指標均優于Hargreaves-Samani 、Chen和Bristow。表明，在相同輸入下，ELM的模擬精度總是高于其他計算模型。

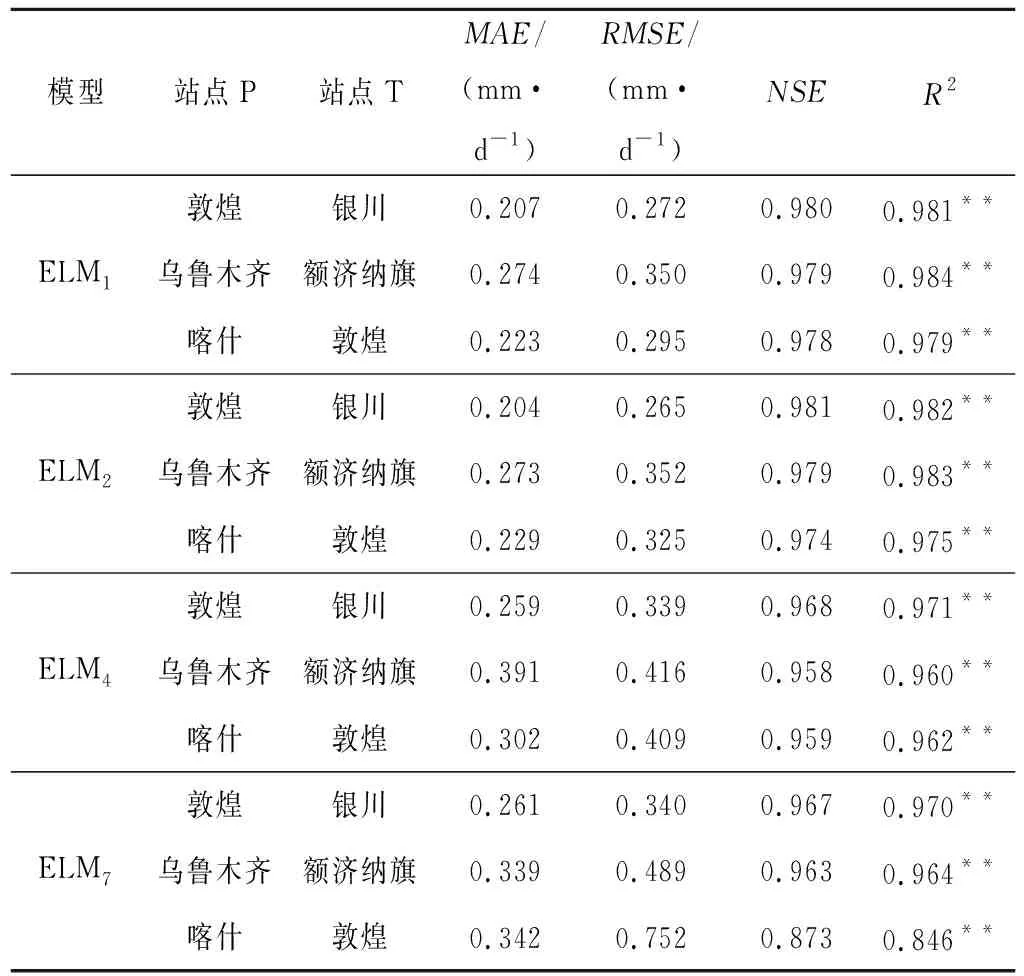
表3 西北地區不同站點間ELM模型可移植性結果Tab.3 ELM portability results among different stations in the northwest region

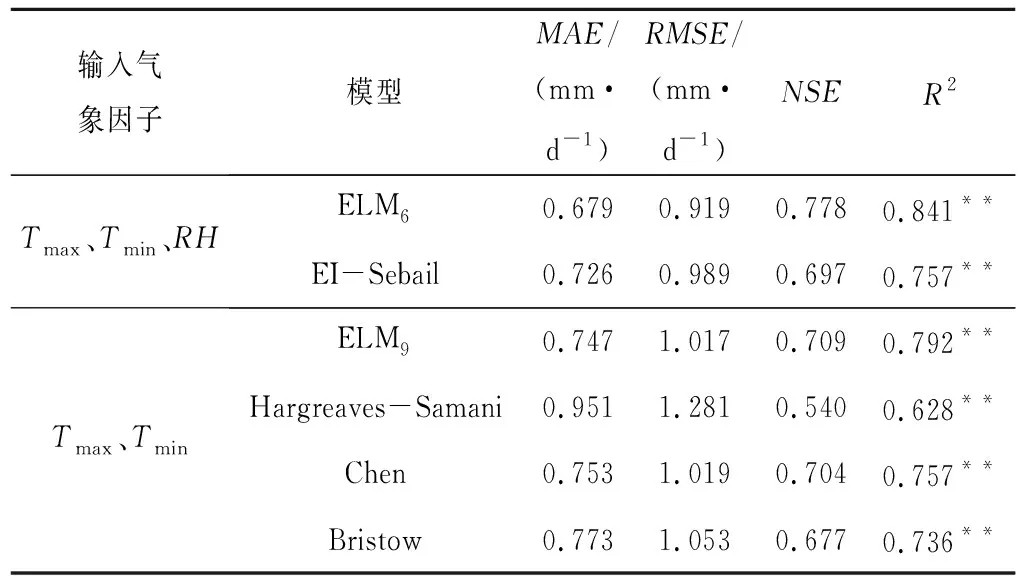
表4 ELM模型與其他物模型模擬精度比較Tab.4 Comparison of simulation accuracy between ELM model and other models

3 結 論

(1)ELM模型在氣象資料缺失情況下，能夠較為精確地預報ET0。ELM2、ELM4及ELM7模型模擬精度均較高，其中ELM7模型從輸入和輸出綜合考慮最為優越，該模型僅需輸入溫度和風速，且MAE和RMSE分別為0.273 mm/d和0.422 mm/d，R2和NSE均能達到0.96 以上，可作為氣象資料缺乏時西北地區ET0預報的推薦模型。

(2)ELM模型可移植性分析表明，在不同站點間利用ELM模型進行ET0預報能夠取得較高精度，ELM模型的泛化性較強。除去ELM7在部分站點的模擬精度相對較低外，其他模型在不同站點之間的模擬精度都很高，MAE、RMSE分別在0.40、0.52 mm/d以下，NSE、R2分別在0.95、0.96以上。

(3)比較在相同輸入情況下ELM模型和其他計算模型的ET0擬精度，ELM模型的模擬精度總是高于其他模型。表明在氣象資料缺乏時，利用ELM進行ET0模擬能取得較好的效果。

(4)本文僅選擇了西北地區的6個站點進行模型構建，可能存在有區域局限性。在后續研究中應以區域實測蒸散量為預報標準值，構建模型，以期為西北地區的精準灌溉實現和區域水管理的嚴格實施提供更加科學的依據。

□