基于重要性測度降維的液壓管路穩健優化設計

張政，周長聰，戴志豪，任哲先，岳珠峰

西北工業大學 力學與土木建筑學院，西安 710129

結構優化設計目的是在滿足約束條件下使結構的某種性能達到最優，其在航空航天等工程領域中已經得到了廣泛應用。然而在傳統的優化設計模型中，設計變量、目標函數和約束函數均為確定性的，沒有考慮客觀存在的不確定性因素的影響，使得優化設計得到的最優解可能對這些不確定因素十分敏感，而這些不確定性因素在多數情況下是不可避免的。基于不確定性的優化設計可以克服傳統優化的這個缺點，使結構滿足可靠性和穩健性的要求[1]。穩健優化設計是基于不確定性的優化設計方法中的一種，其關心的是在參數波動的條件下，結構性能在期望值處的變異程度，即以降低結構性能對參數變異的敏感性為目標[2-4]。穩健優化設計最早由Taguchi提出[5-6]，其思想主要是在不消除不確定性的基礎上通過最小化方差的影響來提升產品性能。隨著非線性規劃的引入，之后的穩健優化設計中同時考慮了目標函數的穩健性及約束條件的穩健性[7-8]。

盡管穩健優化設計相比確定性優化設計具有明顯的優勢，但穩健優化設計需要在優化過程中進行結構響應的不確定性分析，而在很多工程問題中，結構響應的計算需要很高的計算代價，對于包含高維輸入變量的復雜結構而言，所需要的計算成本更高[9]。飛機液壓管路系統中涉及到大量的卡箍，其卡箍的位置布置對液壓管路系統的可靠性有很大影響。因此，飛機液壓管路系統的穩健優化設計問題是一個典型的高維問題，對其卡箍位置優化方法的研究具有重要的意義[10-11]。

通常來說，不同的輸入變量對目標穩健性的貢獻是不相等的，如果對所有的輸入變量進行無差別對待，很可能造成計算資源的浪費，同時也難以得到良好的優化結果[12]。因此，本文基于重要性測度[13-15]提出了一種降維[16]預處理優化方法，所提方法關鍵在于通過重要性測度指標衡量設計變量對優化目標的貢獻程度[17]，進而篩選出對優化目標影響較小的設計變量，并在穩健優化設計中忽略這些變量的影響，最終達到降維目的。

本文首先對飛機局部液壓管路系統的穩健優化設計模型進行了描述。隨后給出了基于參數不確定性下重要性測度指標進行降維處理的具體方法[18]。最終，通過數值算例驗證所提方法的可行性和合理性，并將其應用于工程實例中。

1 飛機局部液壓管路系統的穩健優化設計模型

首先建立考慮管內油液密度、管道內壓、彈性模量等參數的飛機局部液壓管路系統有限元模型。然后，對管路系統施加外部隨機激勵后，對模型進行基于首次超越破壞準則的可靠性分析[19]。最后，考慮管路系統的動力學響應及首超可靠度，建立了穩健優化設計的數學模型。

1.1 液壓系統有限元模型

在ANSYS中采取從局部到整體的建模思路，首先確定了系統管路節點和拐點的位置，然后選取pipe單元建立的有限元模型如圖1所示。

該液壓管路系統模型中的具體相關參數如表1所列。其中，E、μ、ρ、ρf、P、D、δ和Ta為表示管路彈性模量、泊松比、管路密度、管內油液密度、管道內壓、管路外徑、管壁厚度以及環境溫度。除此之外，在具體工作環境中，還需附加支撐約束即卡箍來約束管道的徑向和橫向位移，在圖1中的有限元模型中，將卡箍的支撐作用簡化為末端固定的彈簧單元。21個卡箍的相對位置及所處的節點編號如圖2所示。

考慮在外加激勵后卡箍支撐位置對管路輸出位移響應和速度響應的影響，每個支撐卡箍的位置均由一個三維坐標所確定，但考慮工程實際為了不影響管路結構，僅節點編號為45、62、69、72、75和82的支撐卡箍具有除坐標X方向外其他坐標方向的自由度。因此，在這21個支撐卡箍中選取如表2所示的28個坐標為輸入變量。

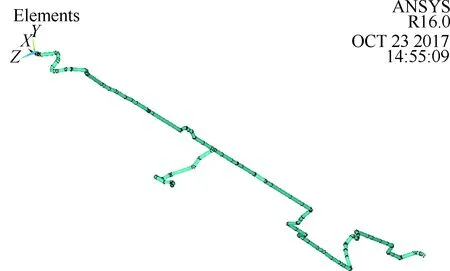
圖1 液壓管路系統的有限元模型Fig.1 Finite element model for hydraulic piping system

表1 液壓管路系統參數Table 1 Parameters of hydraulic pipeline system

ParameterE/MPaμρ/(kg·m-3)ρf/(kg·m-3)P/MPaD/mδ/mTa/℃Value2×1050.37 9001 000250.020.00320

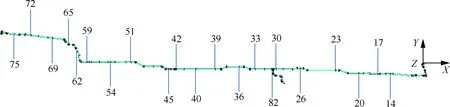
圖2 卡箍位置及節點編號Fig.2 Constraint locations and node indices

表2 變量的選取Table 2 Selection of input variables

Variablesx1x2x3x4x5x6x7x8x9x10x11x12x13x14Position14X17X20X23X26X30X33X36X39X40X42X45X45Z51XVariablesx15x16x17x18x19x20x21x22x23x24x25x26x27x28Position54X59X62X62Y65X69X69Y72X72Y75X75Y82X82Y82Z

Note：In 14X, 14 represents the node number, andXmeans the direction of the coordinate to be considered.

1.2 基于首超準則的可靠性分析

在振動環境中，外場振動激勵通過固定端和每一個卡箍傳遞到管道結構上。采用的激勵形式為加速度功率譜密度(Power Spectral Density, PSD)。激勵方向為坐標Y方向，具體功率譜密度函數如圖3所示。

在施加外部激勵后，本文考慮基于首次超越破壞準則的動力學可靠度，即在Poisson假設下，選擇結構響應峰值超過某個允許的閾值的概率大小作為可靠度評價的準則。單側界限z=b下，隨機過程Z(t)的動力可靠度PR的計算公式為

(1)

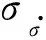
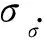
(2)

則動強度可靠性的計算式(1)可以近似為

(3)

管路中任一節點發生失效，整個液壓管路系統即失效，因此，本文所研究的結構可近似為串聯可靠度模型。即該模型整體的可靠度為

(4)

式中：PRi為第i個節點的動力可靠度；n為節點

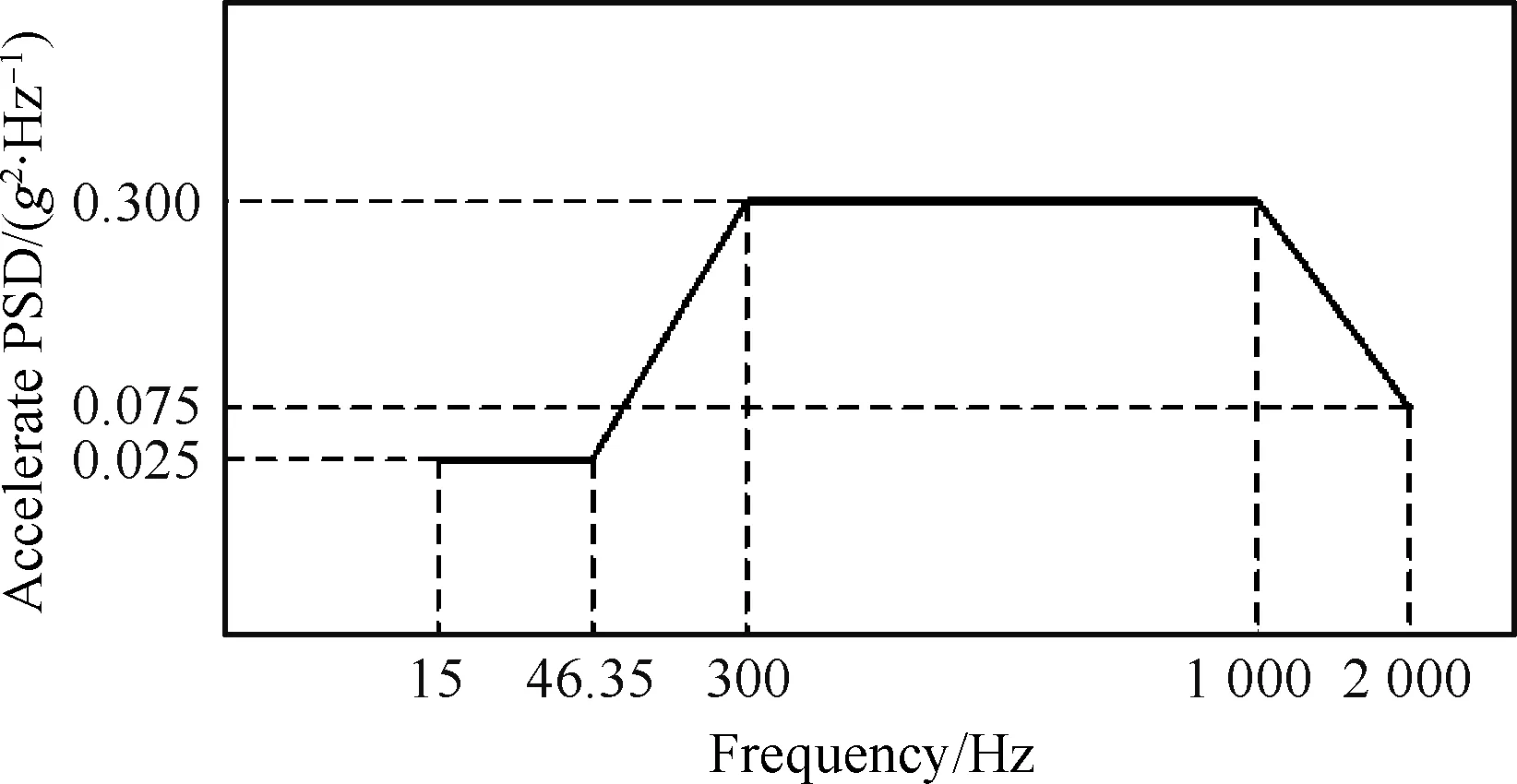
圖3 平穩隨機激勵的加速度功率譜密度函數Fig.3 Acceleration power spectral density function for stationary stochastic excitation

個數，且n=180。由管路振動實驗確定管路的振動應力界限b=200 MPa；T為所給定的額定壽命(10 000個飛行小時)即T=3.6×107s。

綜上，基于首超準則的液壓管路系統可靠性分析過程可總結為：通過有限元分析得到管路系統在隨機激勵作用下的響應，隨后根據計算首超動力可靠度的式(3)得到各節點首超可靠度，最后根據式(4)得到系統首超可靠度。

1.3 局部液壓管路系統的穩健優化設計問題

(5)

式中：設計變量xi為表2所示的卡箍支撐位置坐標；目標函數f為管路系統的最大應力響應Smax；兩個約束條件g1和g2分別為系統最大位移響應約束和系統首超可靠度約束。Smax和Dmax分別為管路系統各節點的最大應力響應及最大位移響應；R為管路系統首超動力可靠度；D*和R*是位移響應及首超動力可靠度的閾值，其取值分別為5.5×10-4m和0.999 9。考慮到在工程實際中，管路系統卡箍支撐位置的變動幅度是有限的，因此在不影響管路基本模型下其初始值x0以及上下界(xU和xL)如表3所示。

由于確定性優化設計并未考慮設計變量中的不確定性因素，而實際工程結構中的不確定性是不可避免的，因此，確定性設計優化可能得到不可行或保守的最優解。穩健優化設計作為一類考慮到隨機不確定性因素影響的設計方法，可以很好地解決上述問題。除此之外，穩健優化設計同時考慮了目標函數的穩健性以及概率約束條件的穩健性。需要注意的是，穩健優化設計是典型的多目標優化問題，可采用加權組合法將多目標問題轉化為單目標問題。綜上，建立確定性優化模型式(5)相對應的穩健優化數學模型為

(6)

式中：取w1=w2=0.5即均值最小和標準差最小在目標函數中所占比重相同，k為概率約束條件需要滿足的可靠度指標，k越大對結構安全性的要求就越高，文中考慮的可靠性指標k=3，此時所對應的約束條件的可靠度為0.998 7。在該穩健性優化模型中，xi被視為服從獨立正態分布的隨機變量，其均值μ為設計變量且其初值和取值范圍與確定性優化模型中的設計變量相同，如表3所示。其中xi的變異系數為0.01。

傳統的穩健優化設計問題需要嵌套雙循環求解，內循環為概率分析，外循環為優化設計。很顯然，每一步外循環中的優化設計迭代，都涉及到大量的概率分析。而本文所研究的局部液壓管路系統的穩健設計優化問題共有28個輸入變量，是一個高維問題，在實際解決的時候需要很高的計算代價，因此需要研究可以減小計算成本的優化方法。

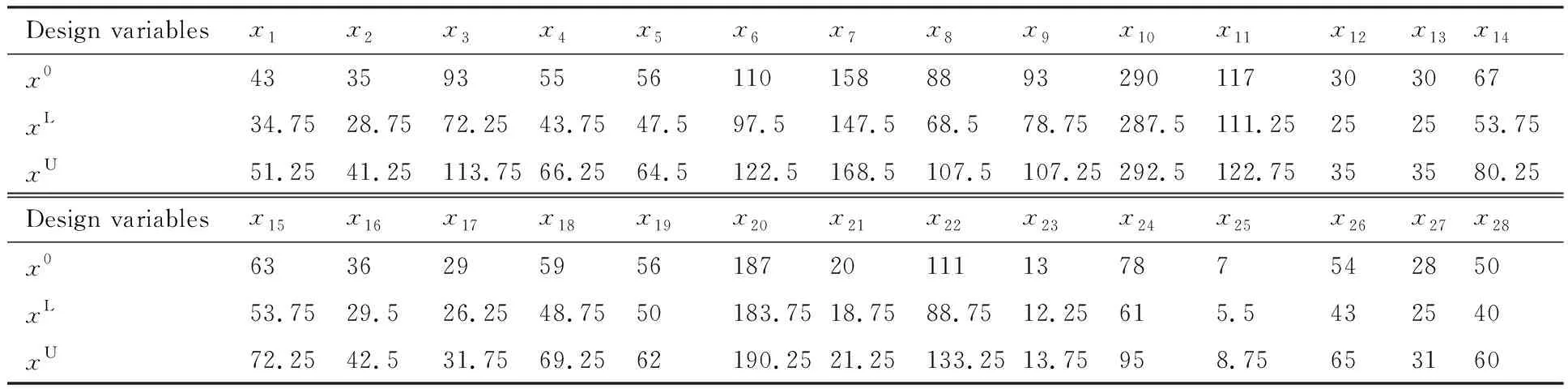
表3 設計變量初值及取值范圍Table 3 Initial values and ranges of design variables mm

2 高維穩健優化設計問題的降維預處理優化方法

在穩健性優化模型中，隨機變量的均值為設計變量，本節引入區間模型對設計變量的不確定性進行描述[21-23]。事實上，隨機變量的分布參數具有區間不確定性的情況可以歸為概率盒問題[24-25]，能夠較全面反映工程中的混合不確定性問題。隨后，給出了區間分布參數下的輸出響應及基于方差的重要性測度指標；最后，基于該指標提出一種高維穩健優化設計問題的降維預處理優化方法。

2.1 區間分布參數下的輸出響應

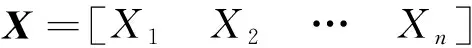
(7)

(8)

若只能給出分布參數θ的取值范圍，并且沒有任何的概率分布信息，可以采用區間模型對分布參數的不確定性進行描述，即θ∈[θL,θU]。則在P維參數空間Θ內上述結構系統輸出響應期望和方差的上下界分別為

(9)

(10)

2.2 區間分布參數下的重要性測度

經典的基于方差的重要性測度指標說明了結構系統中輸入不確定性對輸出不確定性的影響程度，且一階重要性測度即主重要性測度定義為條件期望的方差與總方差的比值，即

“我們想大力支持中小企業，但最大的擔心來自銀企信息不對稱。”某股份制銀行分行中小企業部總經理石斌杰說，“做貸款，當然要摸清企業的情況，比如稅收、社保繳納、公司產值、老板資金狀況、貸款去向等，但這些問題靠目前的征信系統解答不了，增加了辦理貸款的難度。另外，我們很希望有擔保公司來做中小企業的擔保，現在很多企業想貸款，既沒有擔保也不愿給抵押物，這不利于銀行控制風險。”

(11)

參數不確定性條件下，輸出響應的方差為分布參數θ的函數，因此由式(11)可以得出，主重要性測度也是分布參數的函數，可記作Si(θ)。當分布參數的不確定性用區間[θL,θU]來描述時，相應的參數空間內的重要性測度指標的上下界分別為

(12)

2.3 基于重要性測度降維的穩健優化設計方法

基于上述理論，針對高維穩健優化設計問題，可總結出如下的解決思路：

1)通過重要性測度分析得出設計變量對于目標函數的重要性測度指標(如本文所研究的局部液壓管路的穩健優化問題，在引入區間模型描述設計變量分布參數的不確定性的基礎上，得出各設計變量所對應的基于方差的重要性測度指標)。

2)對上述重要性測度進行排序，并以此篩選對優化目標影響較大的設計變量。

3)根據所篩選出的設計變量，建立簡化后的穩健優化設計模型，重新求解。

3 結果與討論

3.1 數值算例

考慮確定性優化問題，其數學模型為

11)2+2(x9-10)2+(x10-7)2+45

s.t.g1(x)=-105+4x1+5x2-3x7+9x8≤0

g2(x)=10x1-8x2-17x7+2x8≤0

g3(x)=-8x1+2x2+5x9-2x10-12≤0

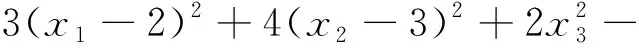
7x4-120≤0

g5(x)=5x1+8x2+(x3-6)2-2x4-

40≤0

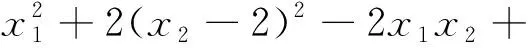
14x5-6x6≤0

g7(x)=0.5(x1-8)2+2(x2-4)2+

g8(x)=-3x1+6x2+12(x9-8)2-

7x10≤0

1≤xi≤10i=1,2,…,10

(13)

在穩健設計優化中，變量xi被考慮成隨機變量，所有變量服從獨立正態分布，其均值為設計變量，變異系數為0.01。相應的穩健優化數學模型為

(14)

式中：常數k取3，相應的可靠度要求為0.998 7；取w1=w2=0.5。

對于上述穩健優化設計問題，采用第1節中提出的方法對優化模型進行一定的預處理，考慮輸入變量的分布參數即上述算例中的均值μxj(j=1,2,…,10)的不確定性對目標函數不確定性的影響程度，采用區間模型對均值的不確定性進行描述，即μxj∈[1,10],(j=1,2,…,10)從而計算得出不確定性參數條件下的重要性測度指標，具體結果如表4所示，圖4采用柱狀圖更直觀的顯示了各變量重要性測度指標的上界。

表4 區間分布參數下的重要性測度指標Table 4 Importance measure indices for interval distribution parameters

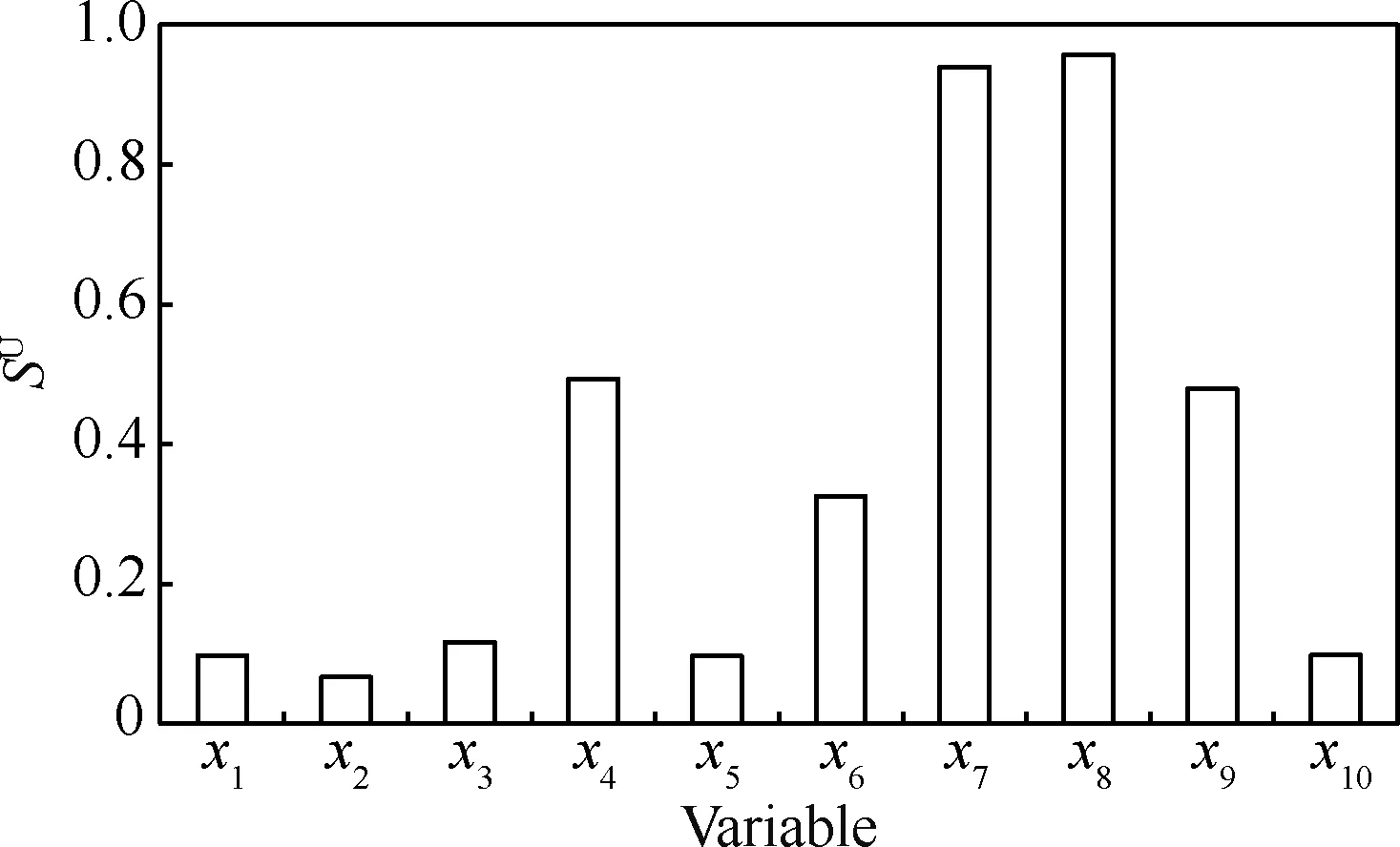
圖4 數值算例重要性測度指標上界Fig.4 Upper bounds of importance measure indices for numerical example

圖4體現了區間分布參數下各變量的不確定性對輸出響應不確定性的最大影響程度，可以看出變量x1、x2、x3、x5和x10的不確定性對輸出響應的影響程度較小，因此在穩健優化設計中，可忽略這五個變量的不確定性，將它們固定為確定值，此時簡化后的穩健優化設計模型為

(15)

對式(14)和式(15)中的兩個模型進行優化計算時需要注意的是，上述含有不確定性的穩健優化設計問題需要嵌套雙循環求解。也就是說，優化過程中的每一步設計迭代，都涉及到目標函數和約束函數均值及標準差的計算。在內循環的概率分析過程中，采用Monte Carlo法對每一步迭代下的μf、σf、μgi和σgi進行計算。在外循環的優化設計中，本文使用SQP進行了最終求解。經過預處理和未經過預處理所得到的優化結果如圖5所示。

由圖5可以看出，預處理之后再進行穩健設計優化，達到收斂時的目標函數調用次數由22次減少到11次，收斂速度大大提高，同時相應的優化效果得到了保證。說明在解決高維穩健優化設計問題中，所提出的方法是可行且有效的。

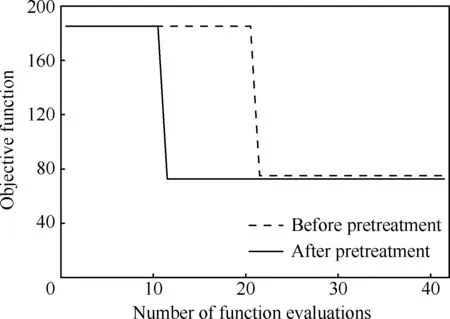
圖5 數值算例優化歷程Fig.5 Optimization history of numerical example

3.2 工程實例

對于1.3節中提出的局部液壓管路系統的穩健優化設計問題，同樣首先進行預處理篩選出對輸出響應(最大應力)影響較大的輸入變量，與3.1節中數值算例類似，卡箍支撐位置的均值μxi(i=1,2,…,28)的不確定性采用區間模型來描述，計算得出的重要性測度指標上界即各變量的最大影響程度如圖6所示。

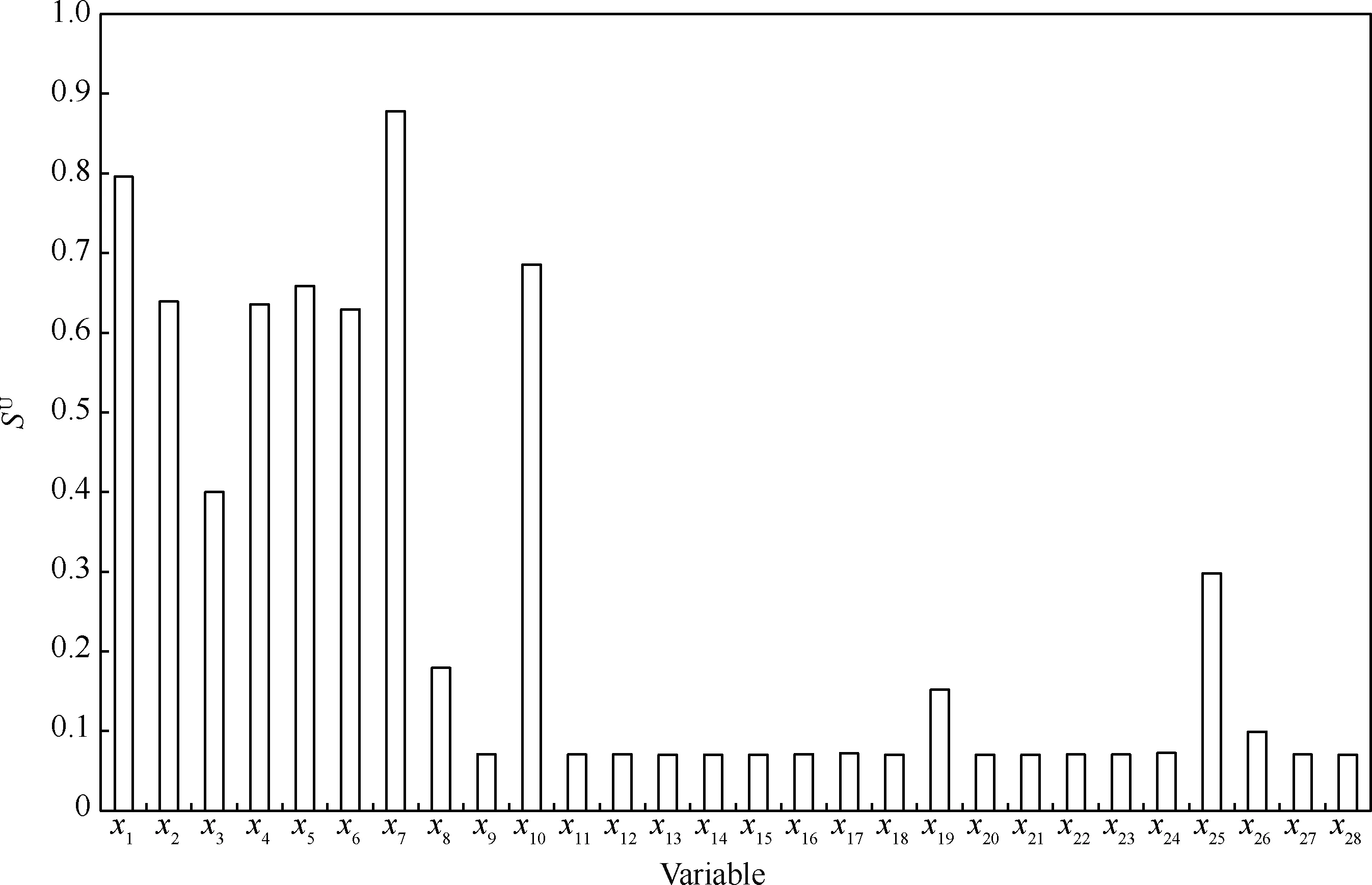
圖6 工程實例重要性測度指標上界Fig.6 Upper bounds of importance measure indices for engineering example

由于所提出的問題包含大量的設計變量，對原問題直接進行優化，所需要的計算成本很高。并且難以得到收斂結果。因此，由圖6可以篩選出對最大應力響應不確定性影響較大的變量，分別為x1、x2、x3、x4、x5、x6、x7、x8、x10、x19、x25和x26。在穩健設計優化中，著重對這12個輸入變量進行優化設計，簡化后的優化模型為

(16)

式中：常數k取3，相應的可靠度要求為0.998 7；取w1=w2=0.5。

與3.1節中數值算例中的計算方法相同，內循環概率分析時采用Monte Carlo法計算每一步迭代設計變量μxi下的μf、σf、μgi和σgi，從而得出每一步設計迭代中的目標函數和約束函數，外循環采用序列二次規劃法進行優化計算，所得到的優化結果及優化歷程分別如表5和圖7所示。

由式(16)可知，飛機局部液壓管路系統穩健優化設計需要在滿足位移響應和動力可靠度的概率約束條件下，優化應力響應的均值同時最小化應力響應的方差。由圖7可以看出經過300次迭代后，反映液壓管路系統應力穩健性的目標函數值逐步收斂。表6給出了優化前后應力穩健性的對比。從該表可以看出，在保證應力響應的均值降低了14.5%的前提下，應力響應的方差降低了71.1%，變異系數降低了66.3%，表明通過穩健優化設計，隨機不確定性因素對飛機局部液壓管路系統應力響應的影響大大降低，進而說明飛機局部液壓管路系統的應力穩健性水平得到了顯著提升。

表5 設計變量優化前后對比

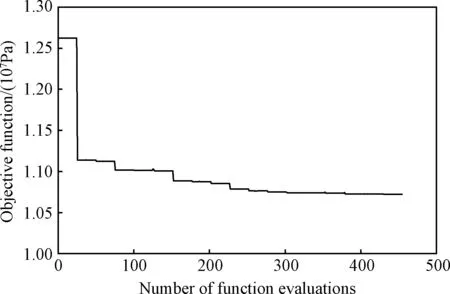
圖7 工程實例優化歷程Fig.7 Optimization history of engineering example

表6 液壓管路系統應力穩健性優化前后對比Table 6 Comparison between initial values and optimized ones for stress robustness of hydraulic piping system

4 結 論

針對不確定環境下飛機局部液壓管路系統的穩健性優化問題，由于其包含高維輸入變量導致所需高昂的計算代價，本文提出了一種基于重要性測度的降維預處理優化方法。考慮輸入變量不確定性和分布參數不確定性同時作用對目標函數的影響，引入區間模型來對隨機變量分布參數的不確定性進行描述。然后給出了對于區間模型描述的不確定性分布參數條件下基于方差的重要性測度指標，參考該指標對設計變量進行篩選從而簡化優化模型。

首先對一數值算例進行穩健優化設計，驗證了所提方法的可行性和合理性。隨后采用該方法對所構建的局部液壓管路系統的優化模型進行優化設計，通過結果分析可以得出當管路中卡箍支撐位置坐標采用優化后的值時，管路系統的應力穩健性得到了提升，并且位移響應約束以及可靠性約束的穩健性也同時得到了保證。

針對高維穩健優化設計問題，本文所提出的方法能夠有效降低計算成本，為復雜工程問題提供了一種高效的解決思路。