低雷諾數下協同射流關鍵參數對翼型氣動性能的影響
許建華,李凱,宋文萍,楊旭東
西北工業大學 翼型葉柵空氣動力學國家級重點實驗室,西安 710072
主動流動控制技術是當前飛行器設計領域的研究熱點,它是顯著提升飛行器性能的重要途徑之一。協同射流(Co-Flow Jet,CFJ)[1]作為一種新興的主動流動控制技術,打破了傳統空氣動力學觀念的束縛,極大地增加了飛行器的升力,并改善了失速特性[2-3],從而使得飛行器的綜合性能得到了革命性的提升。
協同射流概念的提出者、美國邁阿密大學查戈成團隊率先開展了一系列研究工作:針對二維翼型,先后開展了低速和跨聲速狀態下的協同射流增升減阻研究[4-5],結果表明:協同射流翼型不僅可以提高最大升力系數,還可以提高巡航性能[6];采用大渦模擬(Large Eddy Simulation,LES)研究了迎角為30°、大分離流狀態下的協同射流翼型流動混合機理[7],研究了射流動量系數對流場的影響,結果表明:射流動量系數越大,抑制分離能力越強,尾跡區的湍流強度越小;針對三維機翼,開展了基于協同射流主動流動控制技術的超高效、低噪聲、集成式新概念機翼設計[8]以及全機概念設計[9-10]。此外,基于NACA23121翼型開展了協同射流關鍵參數影響規律研究[11-13],結果表明,隨著射流動量系數的增加,阻力減小、有效升阻比降低;吹氣口位置和迎角是影響能量消耗和氣動效率的重要參數;吸氣口位置向后移動,翼型升力和阻力增加。但由于所研究參數的變化幅度偏小,并且只針對迎角為10°的情況展開研究,因此所得結論的普適性有待進一步驗證。隨后,日本Sekimoto等比較了協同射流和反吹介質阻擋放電等離子體激勵器對分離流動的控制效果[14],結果表明:連續或脈沖式的協同射流激勵,以及反吹介質脈沖式激勵均能有效地控制分離。
國內開展協同射流研究的有:北京航空航天大學劉沛清等開展了聯合射流控制技術的數值模擬研究[15],從環量增加和能量注入角度分析了升力增加和延遲分離的機理,結果表明,協同射流控制技術可以有效降低翼型零升迎角、提高翼型的最大升力系數和失速迎角;西北工業大學朱敏等開展了應用協同射流控制的臨近空間螺旋槳高增效方法研究[16],結果表明:采用協同射流技術可以使臨近空間螺旋槳氣動效率提高5%以上;宋超等開展了離散型協同射流的堵塞度和噴口密集度等關鍵參數對流場結構、氣動特性、功率消耗及能量利用率的影響效應與作用規律研究[17],結果表明:堵塞度越高、噴口越密集,增升效果越明顯,但功率消耗更大;許和勇等開展了應用協同射流控制技術的風力機翼型繞流數值模擬[18]以及動態失速控制等研究[19];張順磊等首次通過在翼型內部布置小型風機,實施對翼型的協同射流控制,并利用西北工業大學NF-3大型低速風洞,進行了協同射流的原理性驗證[20],證明了協同射流翼型能夠極大地增加翼型升力、減小阻力和增加失速裕度;南京航空航天大學石雅楠對聯合射流的控制效果和機理也做了一些研究[21],從環量的角度分析了協同射流的增升原理。
綜上所述,國內外對協同射流翼型繞流的數值模擬,大多未考慮氣泵和內部管道,與協同射流的工作原理不符。此外,至今尚未進行射流關鍵參數對翼型氣動性能影響規律的系統性研究。為此,本文利用激勵盤簡化模型模擬氣泵,建立了一種新的協同射流翼型繞流求解方法,并利用低雷諾數下的風洞試驗數據進行了驗證。在此基礎上,開展了低雷諾數條件下射流動量系數、吹/吸氣口的開口尺寸和位置等關鍵參數對射流翼型的氣動性能影響規律研究。
1 協同射流翼型及其受力分析
協同射流主動流動控制技術是美國邁阿密大學查戈成團隊[1]于2004年提出的流動控制新概念技術,指的是在翼型上表面前緣負壓區開口吹氣,在翼型上表面后緣高壓區開口吸氣,在翼型的內部布置氣泵和管道。氣泵將吸入的氣體增壓后從前緣吹氣口噴出,經吸氣口又將等量氣體吸入管道內,如此循環,從而保持吹氣量與吸氣量相等。氣流從上翼面后緣高壓區經管道流向上翼面前緣低壓區,這個過程很容易實現,且能量消耗低。其工作原理如圖1所示。

圖1 協同射流翼型工作原理Fig.1 Operating principle of co-flow jet airfoil
1.1 簡化模型
圖2(a)所示的簡化模型完全忽略了氣泵和內部管道,是目前協同射流翼型數值模擬研究中最常見的簡化方式。
本文引入螺旋槳激勵盤模型[22],提出了一種更符合實際的簡化模型(如圖2(b)所示),即將內部管道中的氣泵簡化成激勵盤。該簡化方式使得翼型受力分析更方便,同時可為氣泵的設計與選擇、內部管道的優化提供可靠的分析手段。
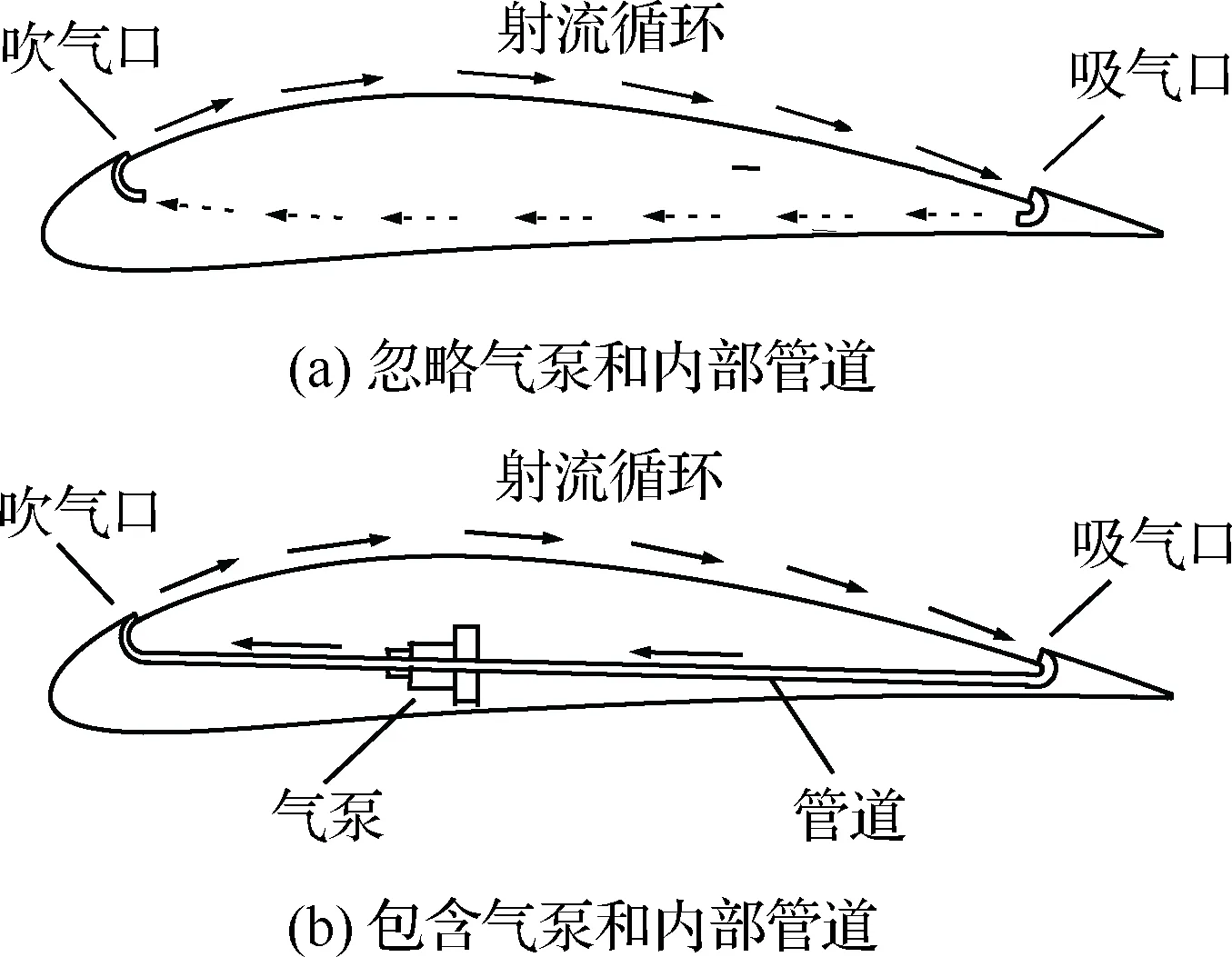
圖2 協同射流翼型的兩種簡化模型Fig.2 Two simplified models of co-flow jet airfoil
1.2 簡化模型受力分析
協同射流翼型在吹、吸氣的同時,會對翼型產生反作用力,因此,在計算翼型的升力和阻力時,必須考慮射流反作用力。
目前大多數研究采用如圖2(a)所示簡化模型,利用控制體分析方法,根據吹氣口和吸氣口處流動參數來計算射流反作用力[23]。該分析模型未考慮內部管道,因此無法計及內部管道所受的壓力和剪切力。
為彌補現有做法的缺陷,便于對協同射流系統進行受力分析,本文采用一種基于激勵盤的簡化模型,即氣泵和內部管道固連于翼型,組成一個完整的受力系統。激勵盤下游的滑流起到加速氣流的作用,而壓力增量產生反作用力,該力可以看做是外力通過激勵盤作用于整個系統(如圖3所示)。因此,在計算氣動力時,除了對翼型表面及內部管道進行壓力和剪切力積分,還要考慮激勵盤的反作用力,保證了協同射流系統受力的完整性。其中,激勵盤反作用力Fr的計算表達式為
Fr,d=(p2-p1)sacos(α+β)
(1)
Fr,l=(p2-p1)sasin(α-β)
(2)
式中:Fr,d為Fr在阻力方向的分量;Fr,l為Fr在升力方向的分量;p1、p2分別為氣泵增壓前后的壓力;sa為氣泵作用處管道的橫截面積;α為來流迎角;β為泵的安裝角(相對于翼型弦線)。若內部管道平行于翼型的弦線,則β為0;若內部管道相對于弦線逆時針旋轉,則β為負;若內部管道相對于弦線順時針旋轉,則β為正。
翼型的阻力D和升力L的表達式為
D=Rd+Fr,d
(3)
L=Rl-Fr,l
(4)
式中:Rd和Rl分別為氣動力(翼型表面和內部管道表面的壓力和剪切力合力的積分)在阻力方向和升力方向的投影。
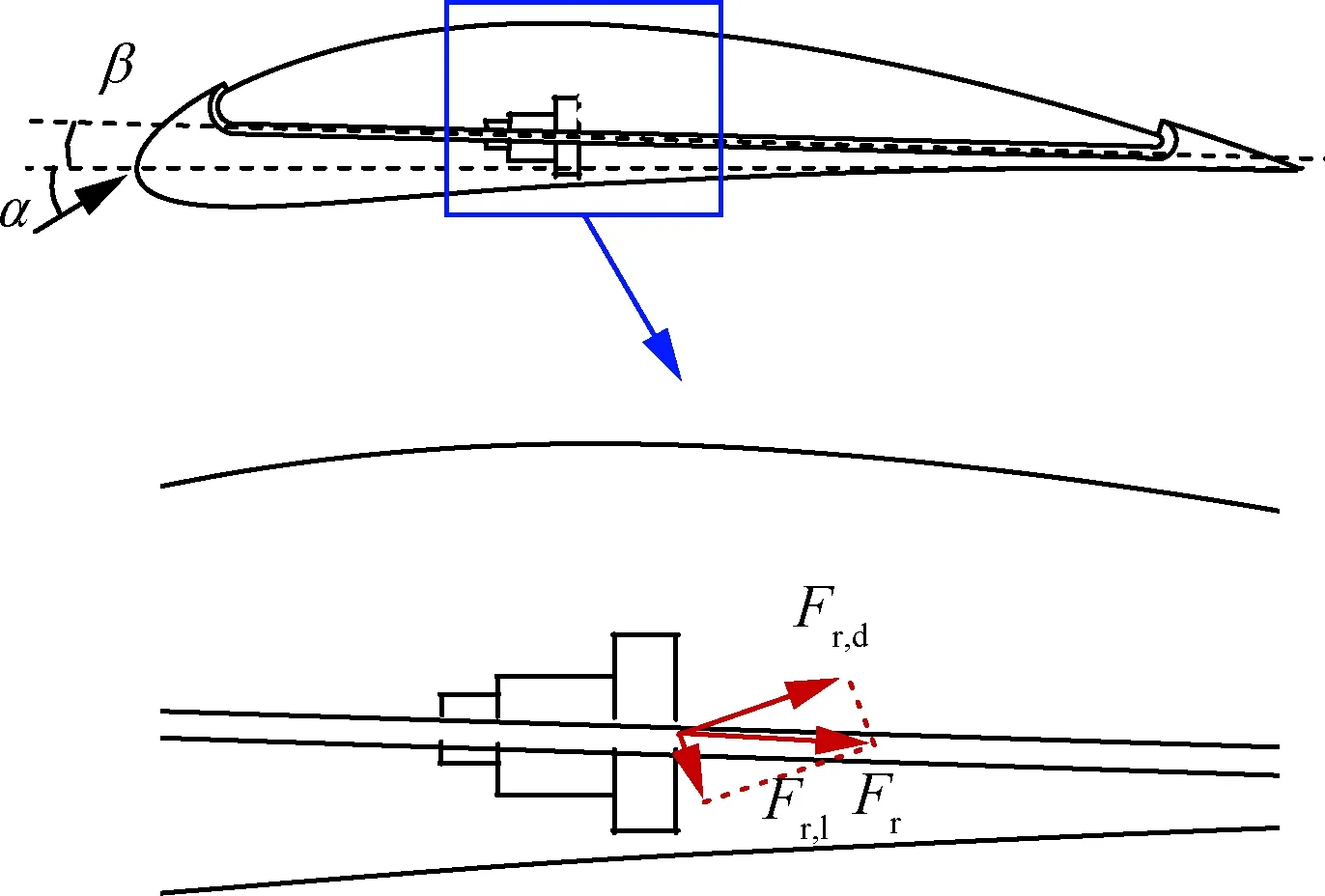
圖3 激勵盤反作用力示意圖Fig.3 Sketch of reaction force of actuator disk model
1.3 協同射流翼型的氣動特性
氣泵功率和氣泵功率系數的定義分別為[4]
(5)
(6)
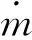
傳統翼型的氣動效率定義為L/D,而協同射流翼型由于采用主動流動控制技術需要額外的能量消耗,因此,在計算氣動效率時,需考慮氣泵的能量消耗。根據文獻[23],將氣泵消耗的功率等效為阻力,定義有效阻力和有效阻力系數,計算表達式分別為
De=D+P/V∞
(7)
CDe=CD+PC
(8)
式中:CD為翼型的阻力系數。同理,考慮氣泵功率消耗的升阻比,定義其為有效升阻比,計算公式為
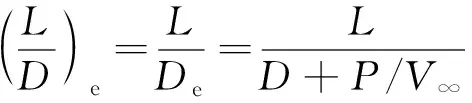
(9)
對于傳統翼型,不存在氣泵,即能量消耗為0,則式(9)退化為傳統翼型的氣動效率計算公式。
為了緩解“掛號難”問題,不少地方推出微信公眾號、自助掛號機、電話等多渠道掛號。但一些號販子趁機鉆空子,除了在醫院放號時段替人搶號外,還轉戰到掛號移動終端搶號,各種掛號APP也隨之產生,一邊是患者下單預約掛號,一邊是號販子接單代掛,動輒加價數百元,侵害了患者正常權益。
2 協同射流關鍵參數
本文涉及射流動量系數、吹氣口尺寸及位置、吸氣口尺寸及位置5個協同射流關鍵參數。
射流動量系數表達式為
式中:Vj為吹氣口射流速度。
吹/吸氣口的開口尺寸及開口位置如圖4所示。圖中x軸方向為翼型弦線方向,y軸方向與x軸垂直。
3 協同射流翼型氣動分析方法及其驗證
3.1 氣動分析方法
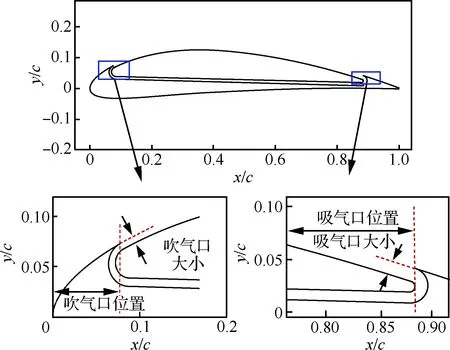
圖4 開口尺寸和開口位置示意圖Fig.4 Sketch of opening size and opening location
基于課題組自主開發的雷諾平均Navier-Stokes(RANS)方程求解程序——PMNS2D[24],建立了適用于協同射流翼型的流動模擬方法。該程序基于結構化網格(點對點搭接多塊網格形式),采用格心有限體積法求解,可實現包括翼型在內的任意二維幾何外形的定常/非定常繞流求解。定常模塊的時間推進格式有龍格-庫塔和LU-SGS(Lower-Upper Symmetric-Gauss-Seidel),非定常模塊的時間推進格式為雙時間法。目前,流動求解程序包含的空間離散格式主要有:中心格式、Roe格式、AUSM(Advection Upstream Splitting Method)類格式等;包含的湍流模型有:B-L(Baldwin-Lomax)、S-A(Spalart-Allmaras)、k-ωSST(Shear Stress Transport)等;包含的流動轉捩預測方法有基于線性穩定性分析的eN方法和Gamma-Theta轉捩模型。為了提高求解效率,相繼引入了當地時間步長、隱式殘值光順、多重網格、低速預處理、MPI(Message Passing Interface)并行等加速收斂技術。
對于傳統常規翼型的流動數值模擬,涉及的邊界條件主要是物面邊界、遠場邊界和交界面邊界。對于協同射流翼型,還需設置激勵盤邊界條件,如圖5所示,圖中p為壓力,ρ為密度,V為速度,下標“1”和“2”分別表示氣泵增壓前后的物理量。在實際計算過程中,通過改變激勵盤邊界處的壓力增量dp,使吹氣口處射流動量系數滿足預定要求。
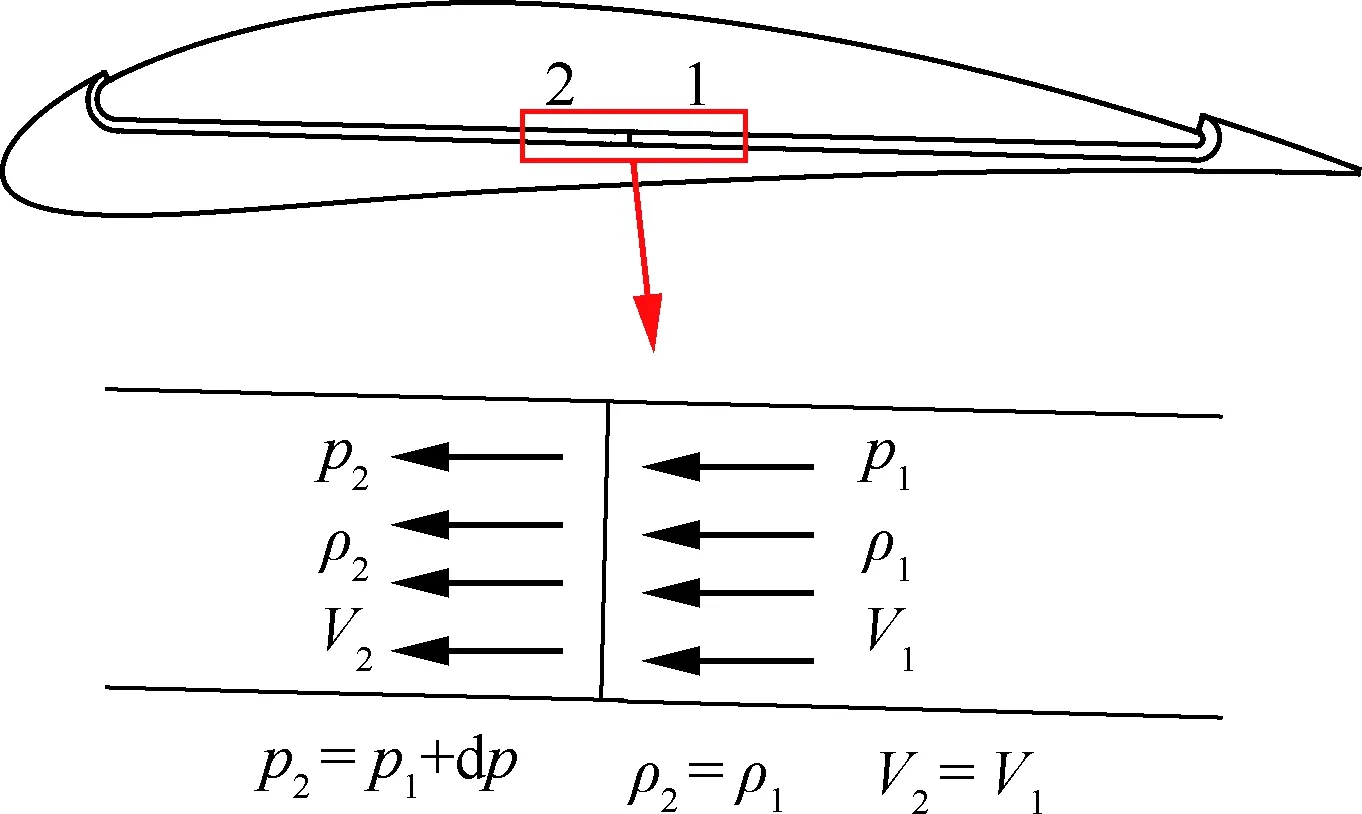
圖5 激勵盤邊界條件Fig.5 Boundary condition of actuator disk model
在本文研究中,空間離散采用Jameson中心格式[25],湍流模型選擇S-A[26],時間推進采用高效的牛頓型隱式LU-SGS[24]。同時,采用了當地時間步長、隱式殘值光順、多重網格、低速預處理等加速收斂措施。
3.2 氣動分析方法驗證
為了驗證所提出的氣動分析方法的正確性,分別對基準翼型NACA6415和協同射流翼型CFJ6415-065-13(吹氣口尺寸為0.65%c,位于7.5%c處;吸氣口尺寸為1.3%c,位于88.5%c處)進行了繞流數值模擬,計算狀態為:來流馬赫數Ma∞=0.03,雷諾數Re∞=2.1×105。通過改變激勵盤邊界處壓力增量dp,使吹氣口處的射流動量系數與參考文獻[4]中一致,以便與試驗值進行對比。試驗采用了前緣固定轉捩,因此本文數值模擬均基于全湍流假設。
圖7為不同迎角下,升力系數(CL)、阻力系數和氣泵功率系數的計算值(CFD)與試驗值(test)對比(圖中Baseline代表NACA6415基準翼型,CFJ代表協同射流翼型)。在升力系數線性段,計算值與試驗值吻合較好,而在大迎角狀態下,計算值與試驗值存在較大誤差,其原因是RANS方法無法準確模擬大分離流動。
基于上述分析,本文所有研究只針對線性段0°、5°和10°迎角的情況,從而確保計算結果和所得結論是可靠性的。
圖8為α=20°時,基準翼型和協同射流翼型的馬赫數云圖和流線圖對比,由圖可知,吹氣口處射流速度很快,具有的能量也很高,射流與主流的湍流混合,使得能量從射流向主流單方向傳遞,克服逆壓梯度能力增強,從而抑制分離的能力增強。
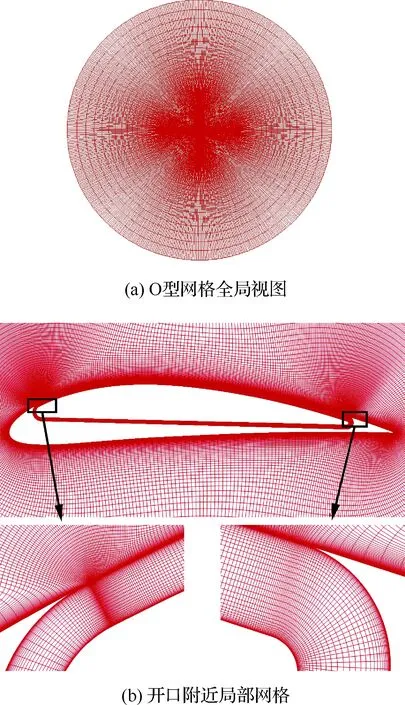
圖6 協同射流翼型CFD求解網格Fig.6 Grids of co-flow jet airfoil for CFD solver
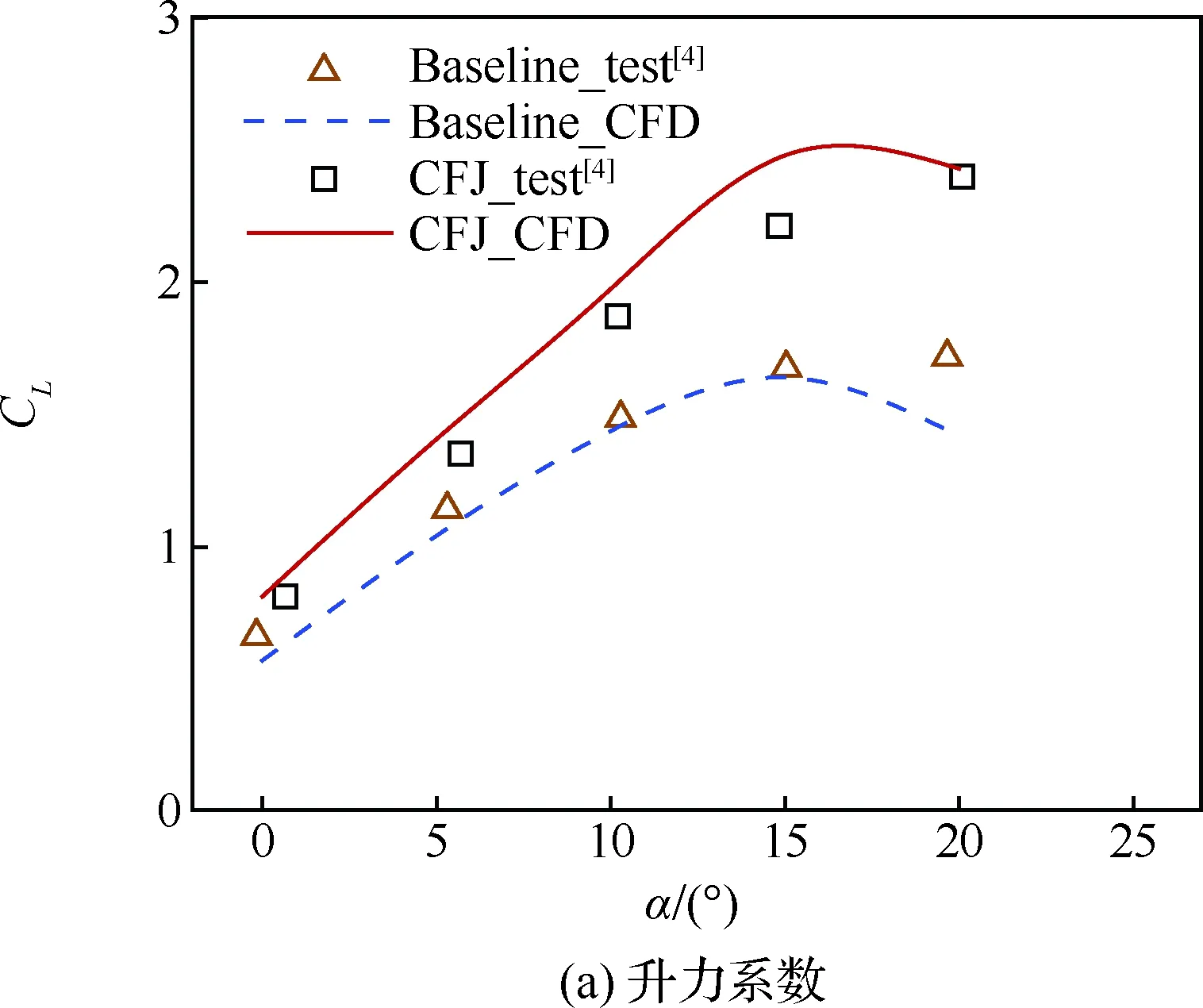
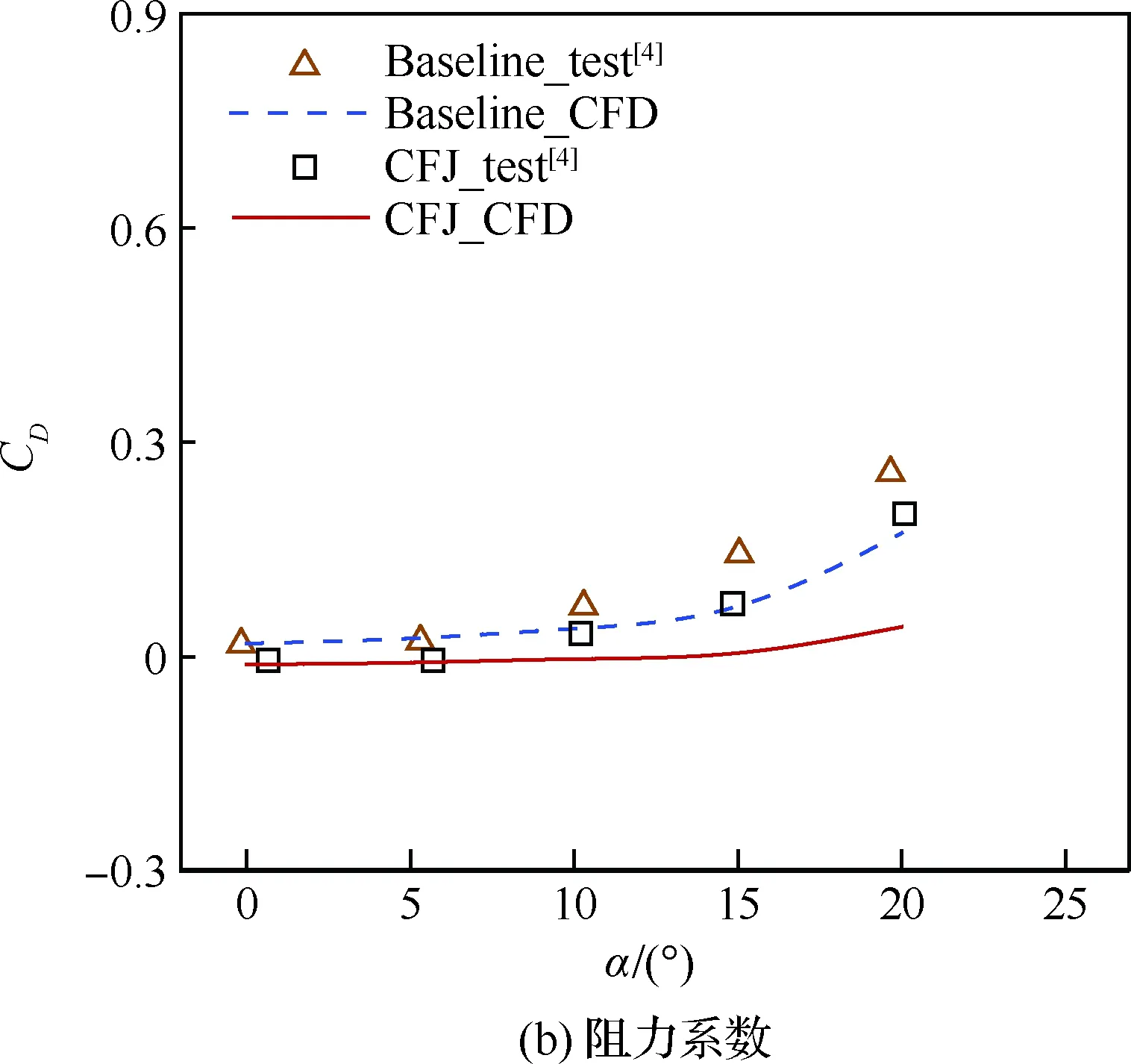
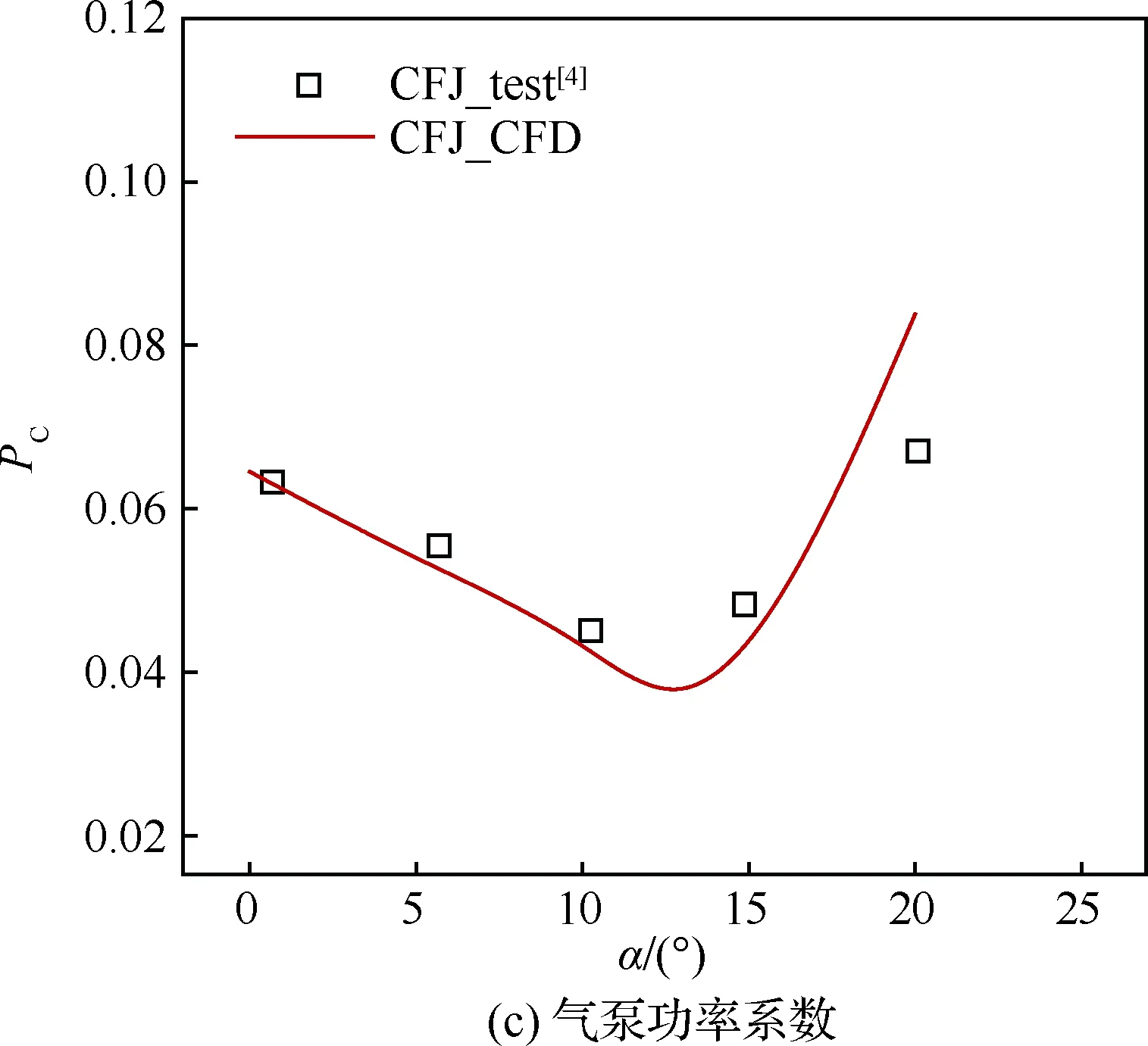
圖7 升力系數、阻力系數、氣泵功率系數計算值與 試驗值的對比Fig.7 Comparison of CL, CD, PC between CFD results and test data
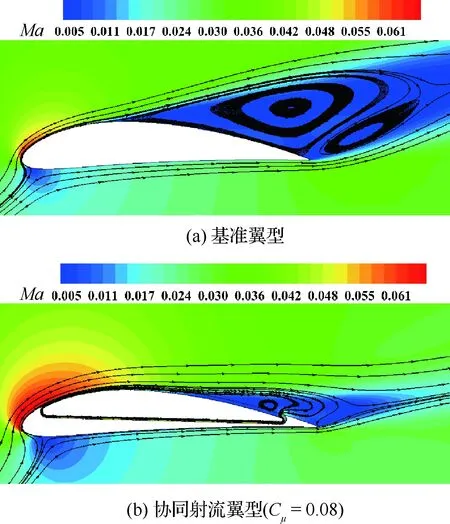
圖8 基準翼型和協同射流翼型的馬赫數云圖和 流線圖對比(α=20°)Fig.8 Comparison of Mach number contours and streamlines between baseline and co-flow jet airfoil (α=20°)
圖9為α=20°時基準翼型和協同射流翼型的壓力系數(Cp)分布對比,由圖可知:相比于基準翼型,協同射流翼型的上表面具有更大的負壓,形成更大的前緣吸力效應,從而升力系數顯著增加。此外,從圖8流線圖和圖9壓力系數曲線可以看出,協同射流翼型下表面的前緣駐點位置明顯后移,意味著有效迎角顯著提高,這也是升力系數能夠明顯提高的重要原因之一。
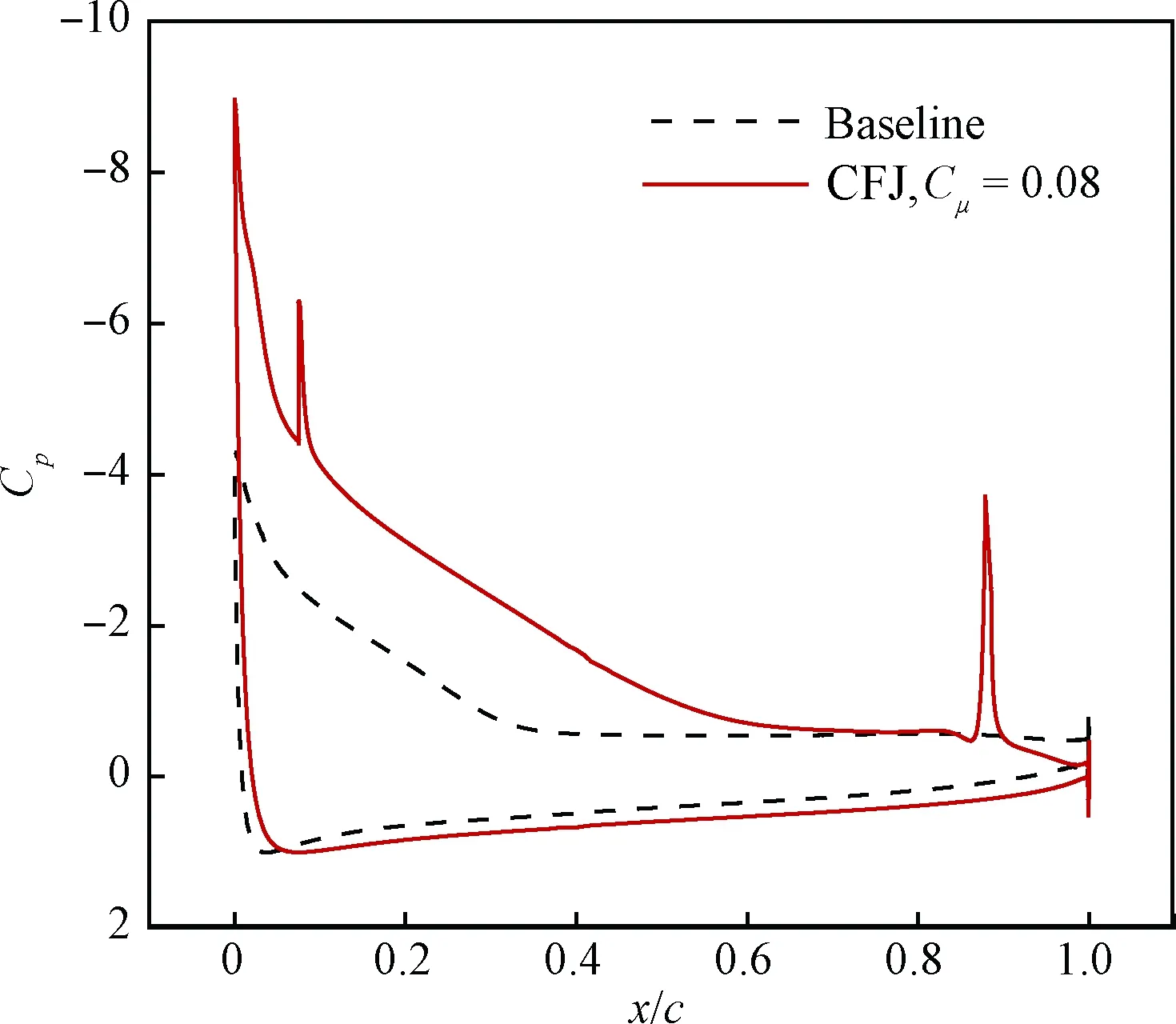
圖9 基準翼型和協同射流翼型壓力系數分布 對比(α=20°)Fig.9 Comparison of pressure coefficient distribution between baseline and co-flow jet airfoil (α=20°)
4 關鍵參數的影響規律
本文以文獻[4]給定的射流動量系數Cμ=0.08、開口尺寸(吹氣口為0.65%c、吸氣口為1.3%c)、 開口位置(吹氣口位于7.5%c處、吸氣口位于88.5%c處)為基準,開展協同射流關鍵參數影響規律研究,計算狀態固定為Ma∞=0.03,Re∞=2.1×105。
4.1 射流動量系數的影響
保持其他參數固定不變,在迎角分別為0°、5°和10°時,研究了射流動量系數對升力系數、有效阻力系數、有效升阻比和氣泵功率系數的影響規律及機理。
由圖10可知,射流動量系數超過0.03時,射流翼型的升力系數大于基準翼型。對于迎角為0°和5°的附著流動,射流翼型消耗的氣泵功率系數PC高于翼型阻力系數CD的減小量,導致其有效阻力高于基準翼型,有效升阻比沒有明顯提高,甚至下降;而當迎角達到10°時,流動出現較大的分離,射流翼型能夠以較小的功率消耗抑制分離,從而獲得較大的減阻收益,導致其有效阻力顯著低于基準翼型,有效升阻比顯著高于基準翼型。
迎角為0°和5°時的氣動性能變化規律相近,即隨著射流動量系數增加,升力系數逐漸增加,有效阻力系數先減小后增加,有效升阻比先增加后減小,氣泵功率系數增加較快。隨著迎角增加,最大升阻比對應的射流動量系數也增加。
迎角為10°時,射流動量系數在0.016~0.037 范圍內,氣動力變化最為顯著;隨著射流動量系數增加,升力系數先緩慢增加,然后迅速增加,最后緩慢線性增加;有效阻力系數先緩慢減小,然后迅速減小,最后逐漸增加;有效升阻比先緩慢增加,然后迅速增加,達到最大升阻比后又迅速下降;氣泵功率系數經歷先增加,后減小,再增加的復雜過程。
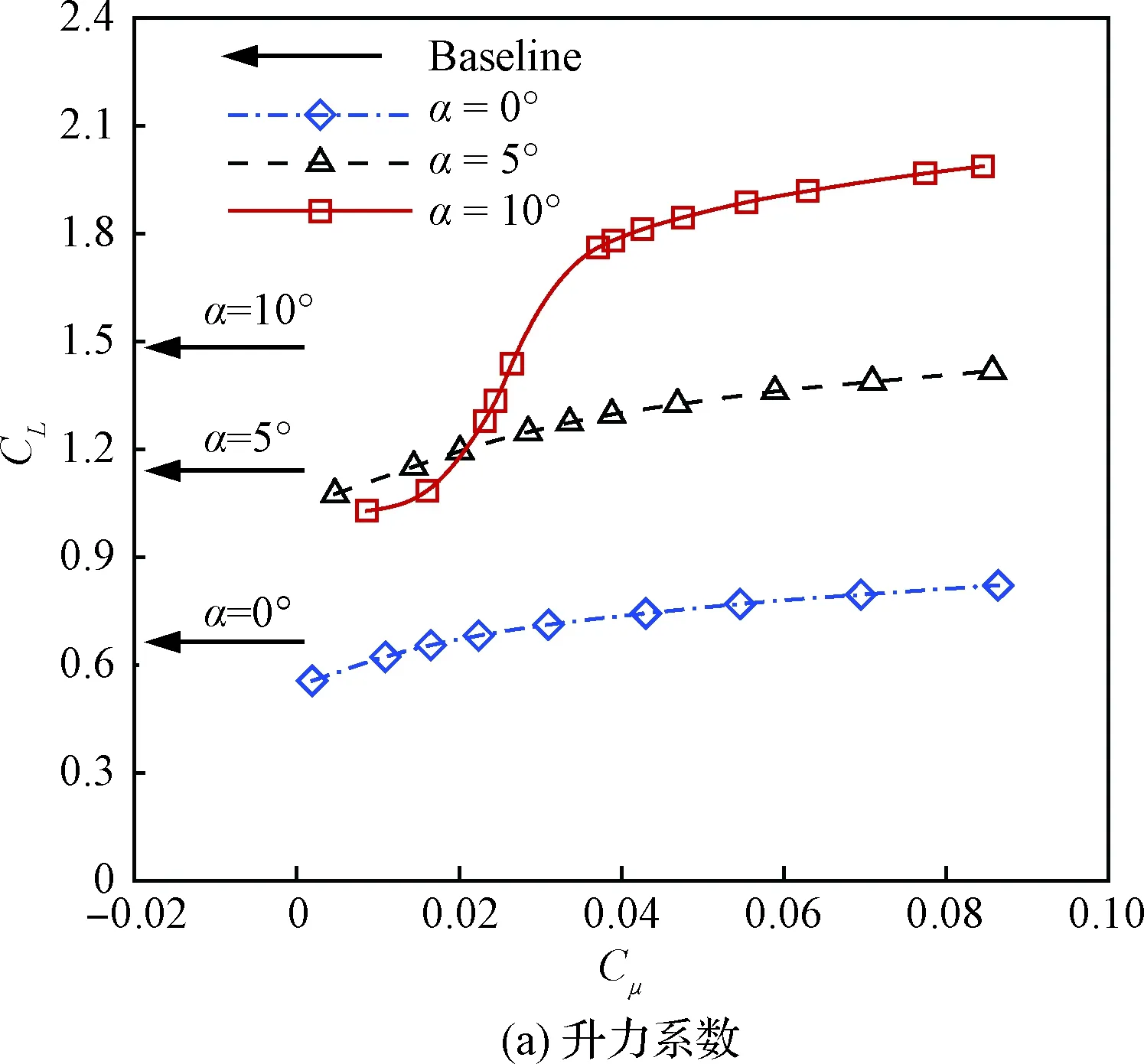
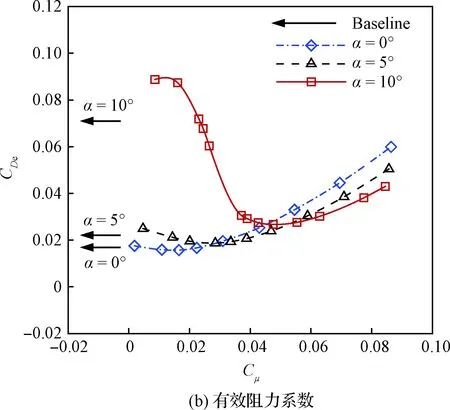
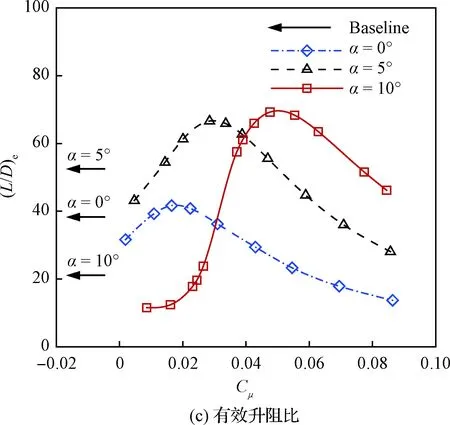
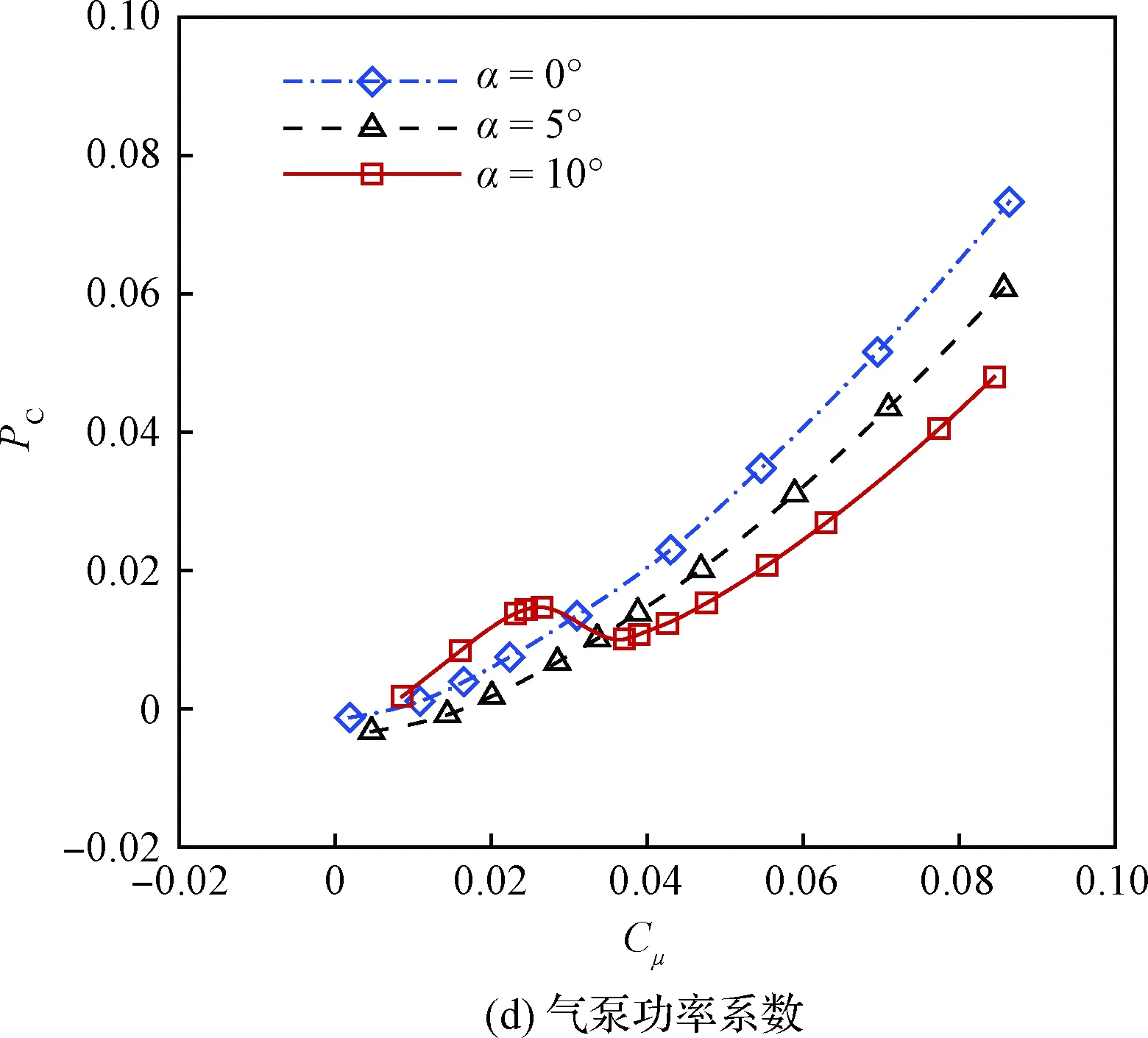
圖10 射流動量系數對氣動性能的影響Fig.10 Effects of jet momentum coefficient on aerodynamic performance
為了揭示迎角為10°時變化規律的本質,分別給出了射流動量系數為0.016、0.026和0.037的馬赫數云圖和流線圖,如圖11所示,分別對應氣動力發生顯著變化的起始點、氣泵功率系數極大值和極小值等狀態。可以看出,迎角為10°時,射流動量系數增加到0.016,翼型上翼面仍然存在明顯的分離流動,因此氣動力并未出現明顯變化;隨著氣泵功率系數進一步增加,能量注入更大,上翼面分離區減小,氣動力發生了顯著變化;當射流動量系數增加到0.026時,氣泵功率系數達到局部極大值,但上翼面仍然存在較大分離區;隨著射流動量系數進一步增加,分離區進一步逐漸減小,升阻特性仍然變化顯著,當射流動量系數增加到0.037時,分離區基本消失,此時氣泵功率系數達到局部極小值;當流動分離被完全抑制時,隨著射流動量系數增加,升阻特性變化規律與小迎角狀態類似。
此外,相同射流動量系數下,5°迎角的氣泵功率系數均小于0°迎角的氣泵功率系數,原因是5°迎角的前緣負壓更大,后緣吸氣口和前緣吹氣口的壓差更大,因此更容易形成協同射流循環,這也是協同射流高效的重要原因。但是,10°迎角下,大分離流動導致后緣吸氣口與前緣吹氣口之間的壓差小,達到相同的射流動量系數時所消耗的氣泵功率更大;而當射流動量系數增加到完全抑制分離流動時,相同射流動量系數下的氣泵功率消耗又是最低的。
綜上,迎角為10°時的變化規律比其他小迎角時的變化規律更為復雜的根本原因是迎角為10°時存在大分離流動,分離流動導致氣泵功率增加,并且隨著射流動量系數增加,流動分離被逐漸抑制,氣動力變化也最為劇烈。
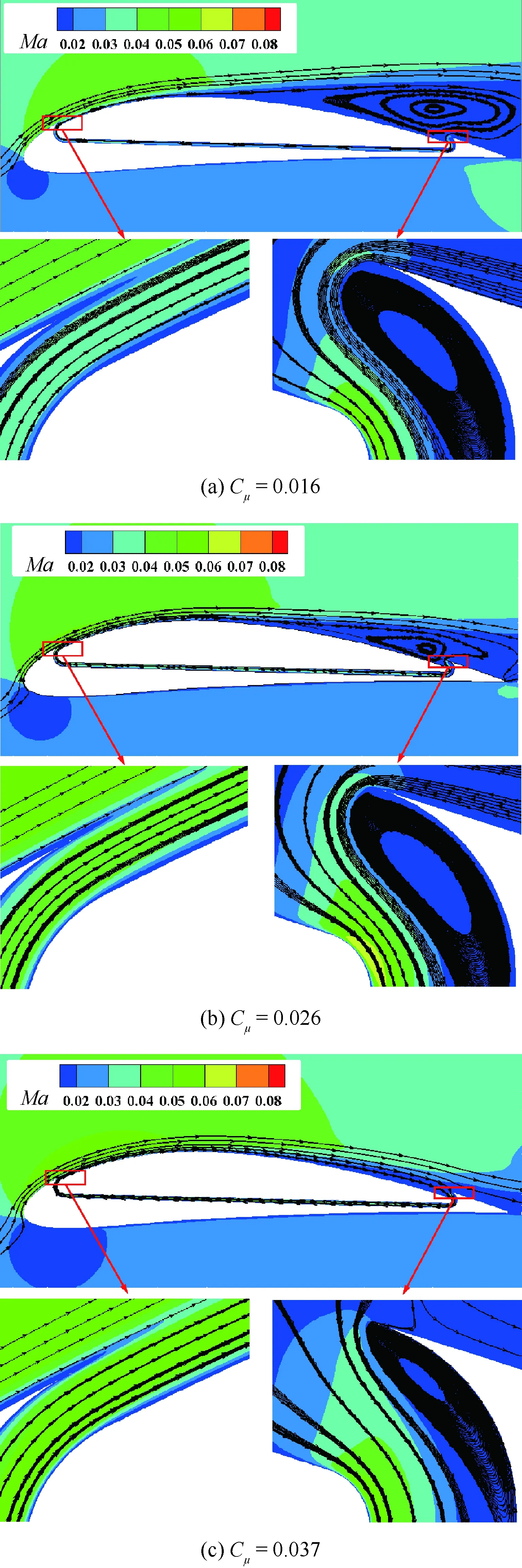
圖11 不同射流動量系數下的馬赫數云圖和 流線圖(α=10°)Fig.11 Mach number contours and streamlines for different jet momentum coefficients(α=10°)
4.2 吹氣口尺寸的影響
保持其他參數不變,在迎角分別為0°、5°和10°時,研究了吹氣口尺寸對升力系數、有效阻力系數、有效升阻比和氣泵功率系數的影響規律及機理。吹氣口尺寸變化范圍為0.52%c~1.30%c,如圖12所示。
由圖13可知,隨著吹氣口尺寸增加,升力系數幾乎不變;有效阻力系數先減后增,并且迎角越大,最小有效阻力系數對應的吹氣口尺寸越小;有效升阻比先增后減,并且迎角越大,最大升阻比對應的吹氣口尺寸越小;氣泵功率系數的變化規律與有效阻力系數的變化規律基本一致,說明氣泵功率系數在有效阻力系數中占主導地位。
圖14給出了迎角為10°時,不同吹氣口尺寸的馬赫數云圖和流線圖。在射流動量系數相同的條件下,隨著吹氣口尺寸增加,吹氣口速度減小,導致氣泵功率系數減小,從而有效阻力系數減小、有效升阻比增加。當吹氣口尺寸達到0.91%c時,氣泵功率系數和有效阻力系數最小,有效升阻比最大,但此時吸氣口處的速度較低,必須從吸氣口上方吸入更多的氣流才能保證與吹氣口相等的質量流量,因此在吸氣口管道內形成一個小的分離渦。當吹氣口尺寸進一步增加時,吹氣口速度進一步減小,甚至無法維持附著流動,同時吸氣口管道內形成更嚴重的分離渦,導致氣泵功率系數和有效阻力系數反而增加,從而有效升阻比減小。因此,每一個迎角下,均存在一個最佳吹氣口尺寸,使得氣泵功率系數最小、有效升阻比最大。
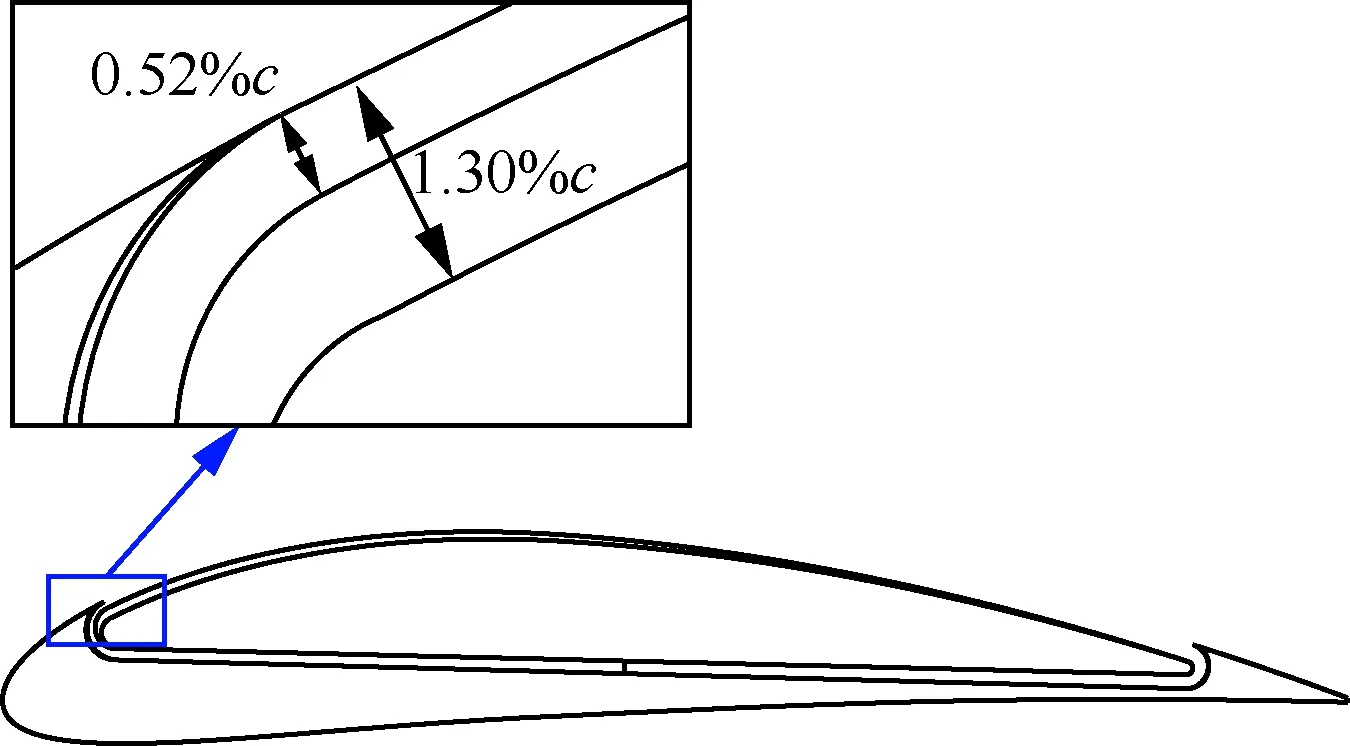
圖12 最小和最大吹氣口尺寸示意圖Fig.12 Sketch of minimum and maximum injection sizes
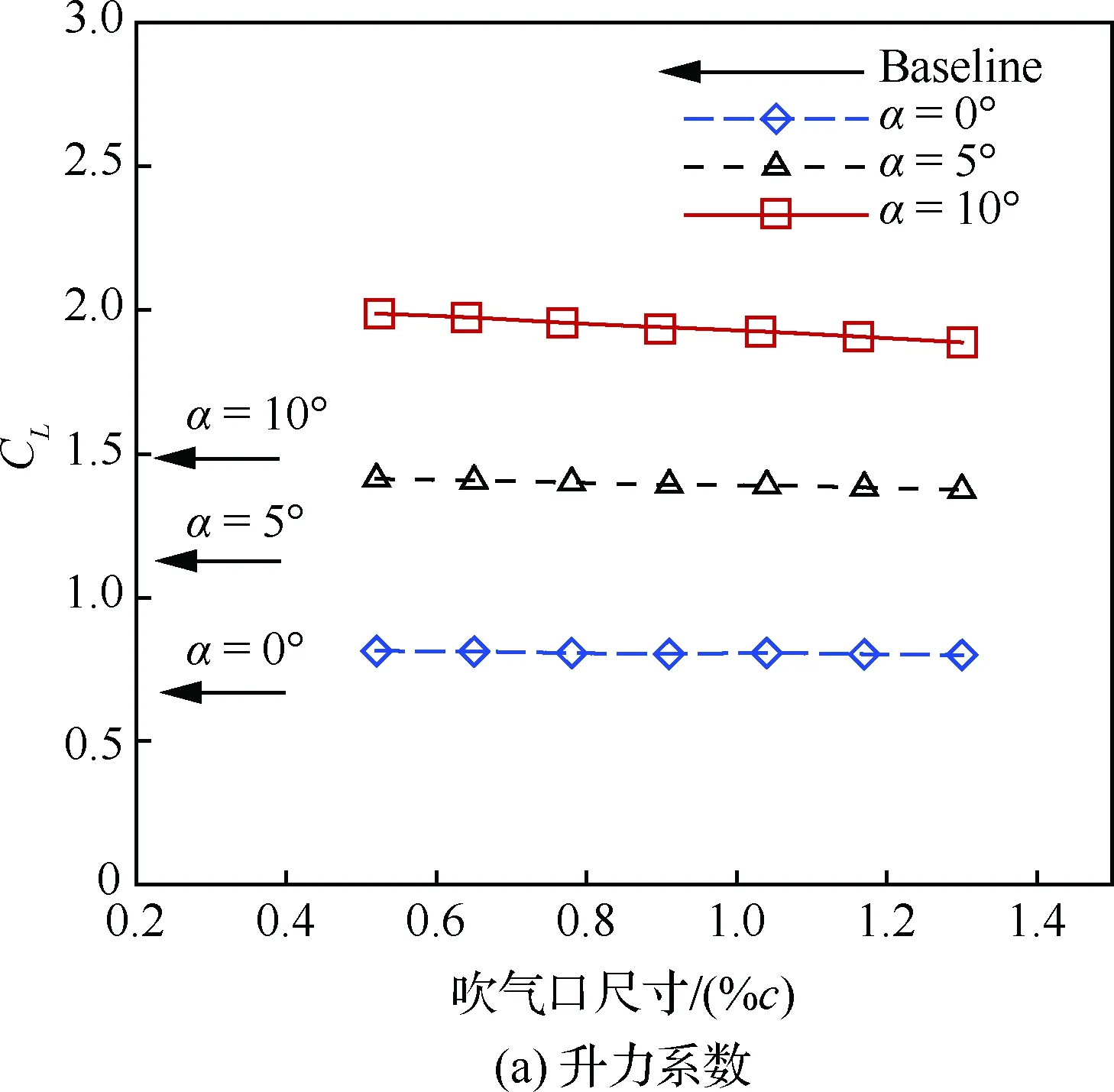
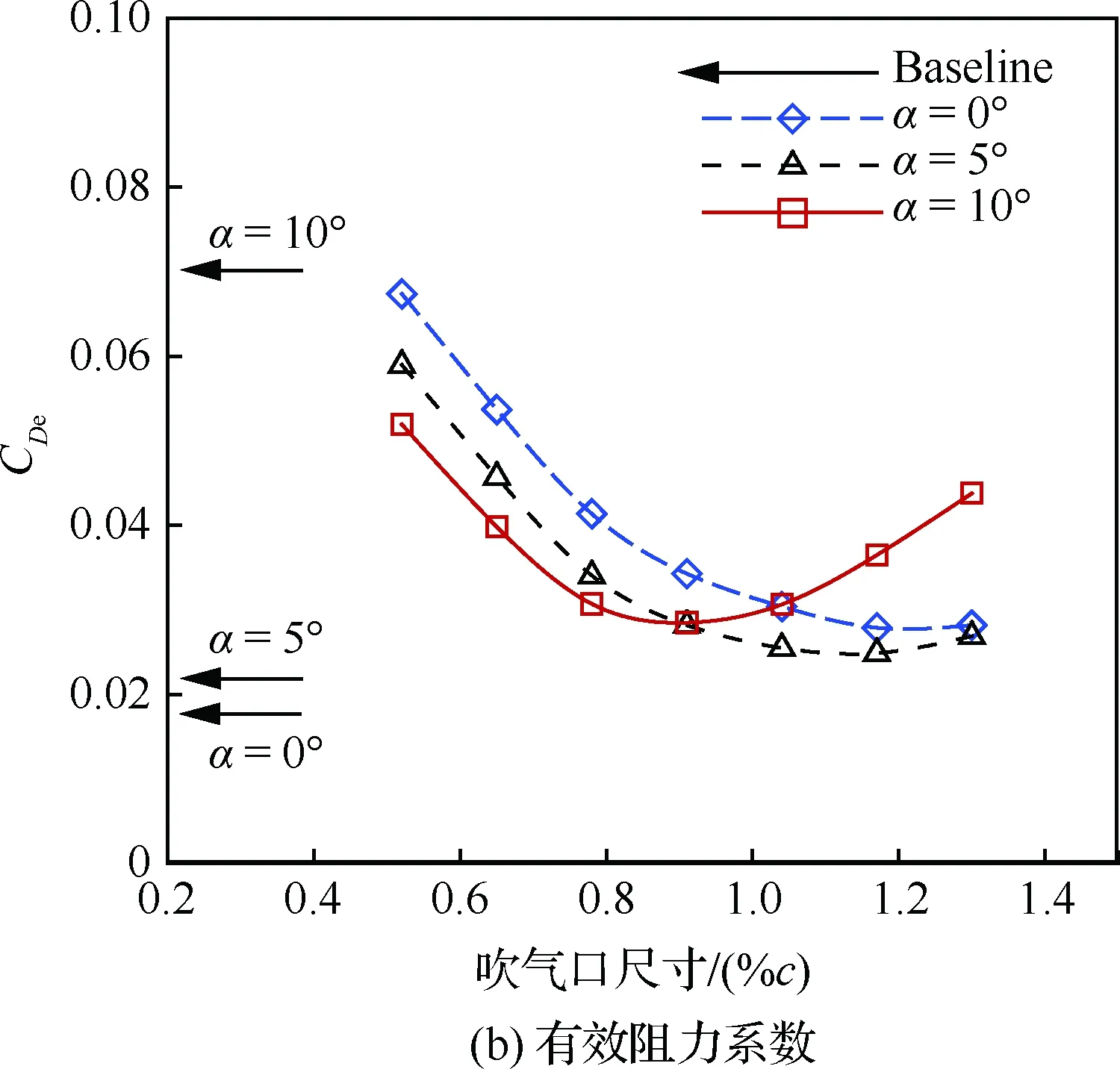
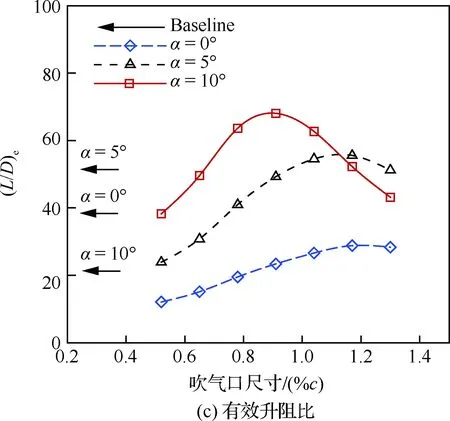
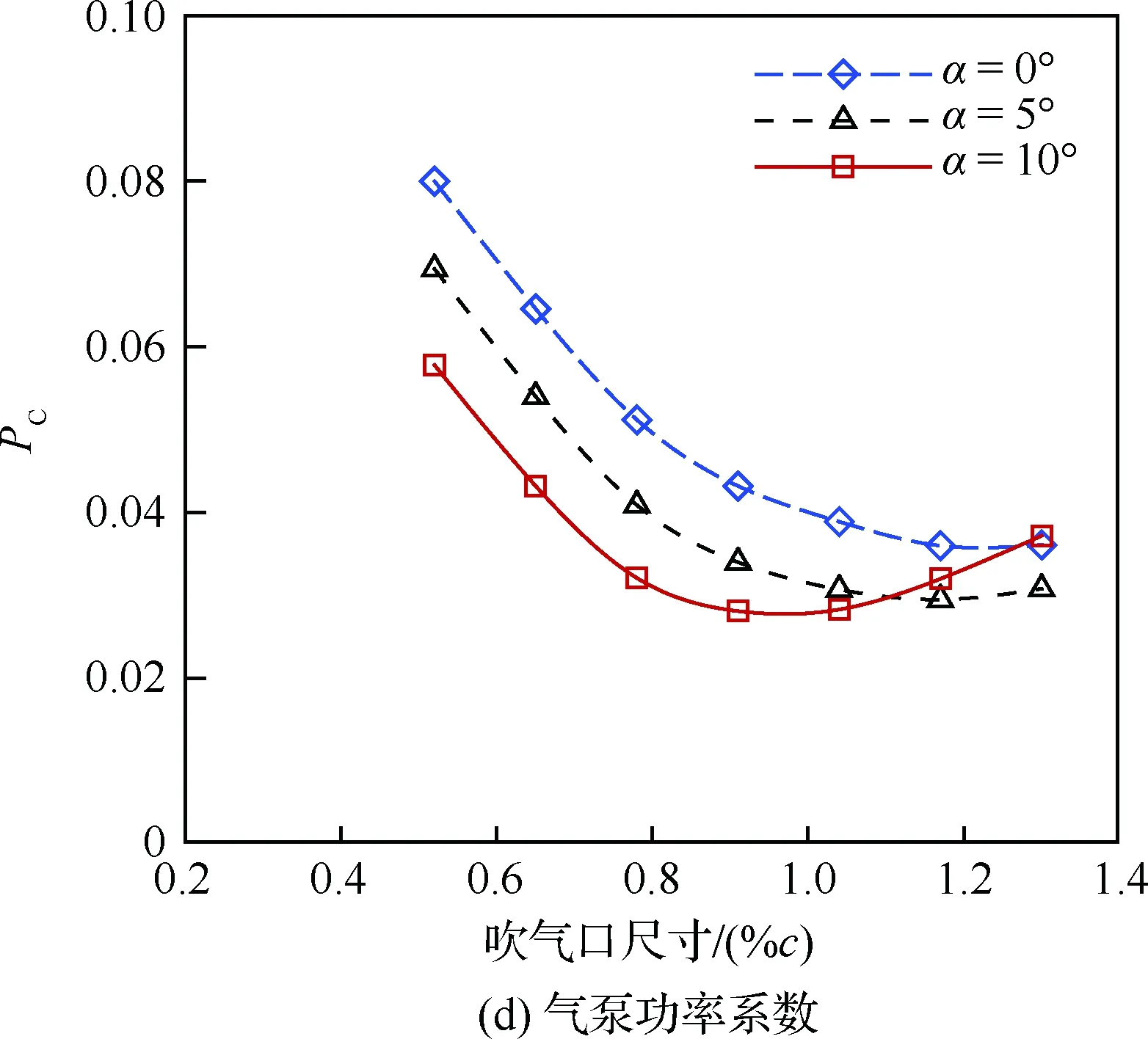
圖13 吹氣口尺寸對氣動性能的影響(Cμ=0.08)Fig.13 Effects of injection size on aerodynamic performance (Cμ=0.08)
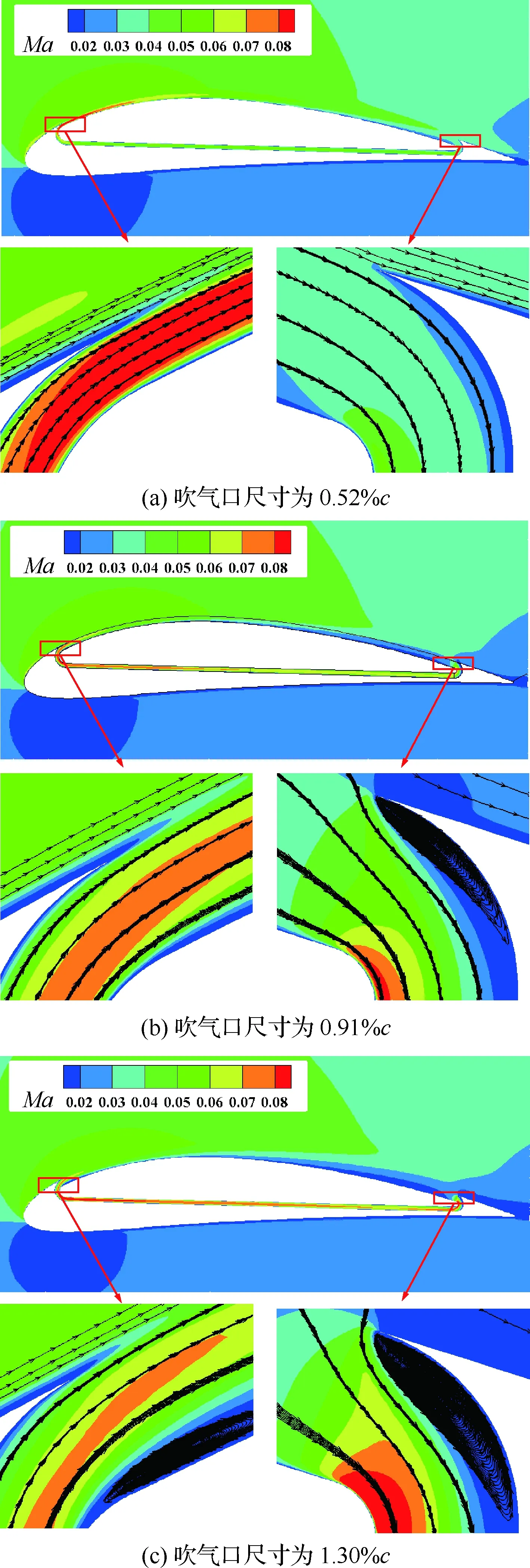
圖14 不同吹氣口尺寸下的馬赫數云圖和流線圖(α=10°)Fig.14 Mach number contours and streamlines for different injection sizes (α=10°)
4.3 吹氣口位置的影響
保持其他參數不變,在迎角分別為0°、5°和10°時,研究了吹氣口位置對升力系數、有效阻力系數、有效升阻比和氣泵功率系數的影響規律及機理。吹氣口位置變化范圍為4.5%c~9.0%c,如圖15所示。
由圖16可知,相對于吹氣口尺寸,吹氣口位置的變化對升力系數幾乎沒有影響,對有效阻力系數、有效升阻比和氣泵功率系數的影響很小,且無明顯規律。分析其原因主要是,不同吹氣口位置引起的翼型前緣吹氣口附近的負壓變化并不顯著,同時后緣吸氣口處的壓力系數分布基本不變,如圖17所示。
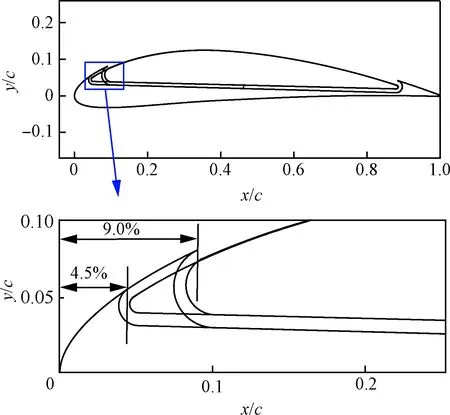
圖15 最小和最大吹氣口位置示意圖Fig.15 Sketch of minimum and maximum injection locations
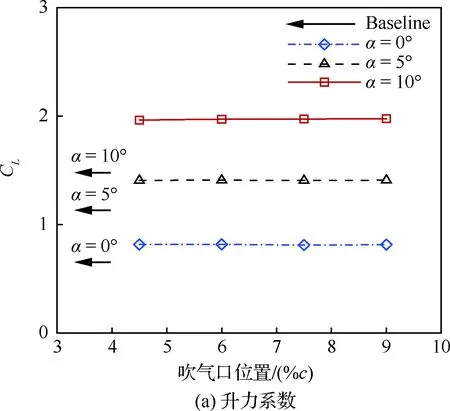
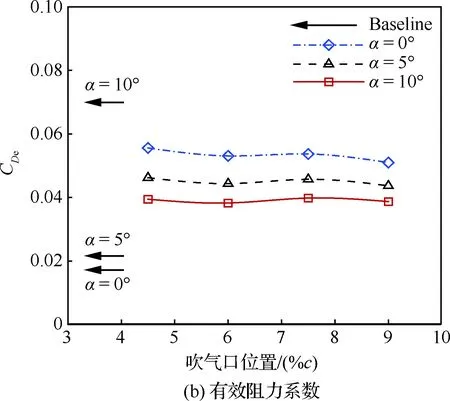
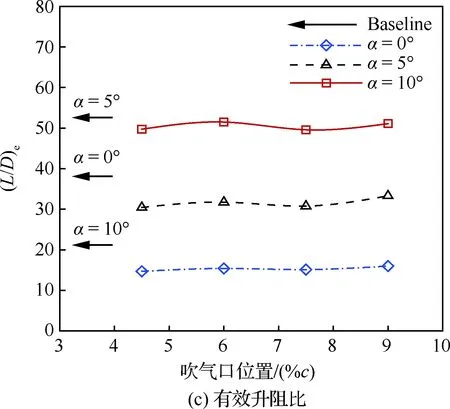
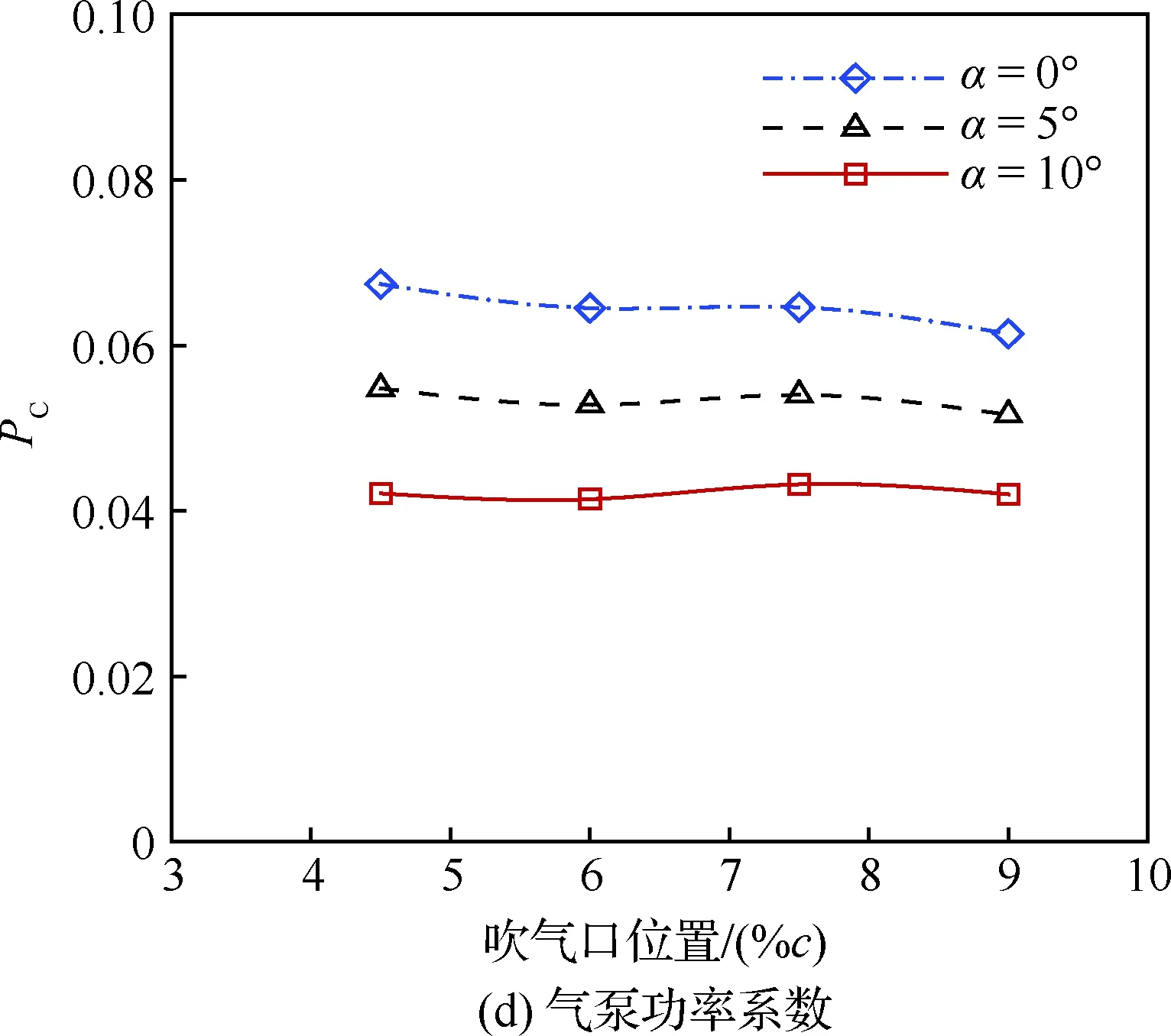
圖16 吹氣口位置對氣動性能的影響(Cμ=0.08)Fig.16 Effects of injection location on aerodynamic performance (Cμ=0.08)
4.4 吸氣口尺寸的影響
保持其他參數不變,在迎角分別為0°、5°和10°時,研究了吸氣口尺寸對升力系數、有效阻力系數、有效升阻比和氣泵功率系數的影響規律及機理。吸氣口尺寸變化范圍為0.78%c~1.82%c,如圖18所示。
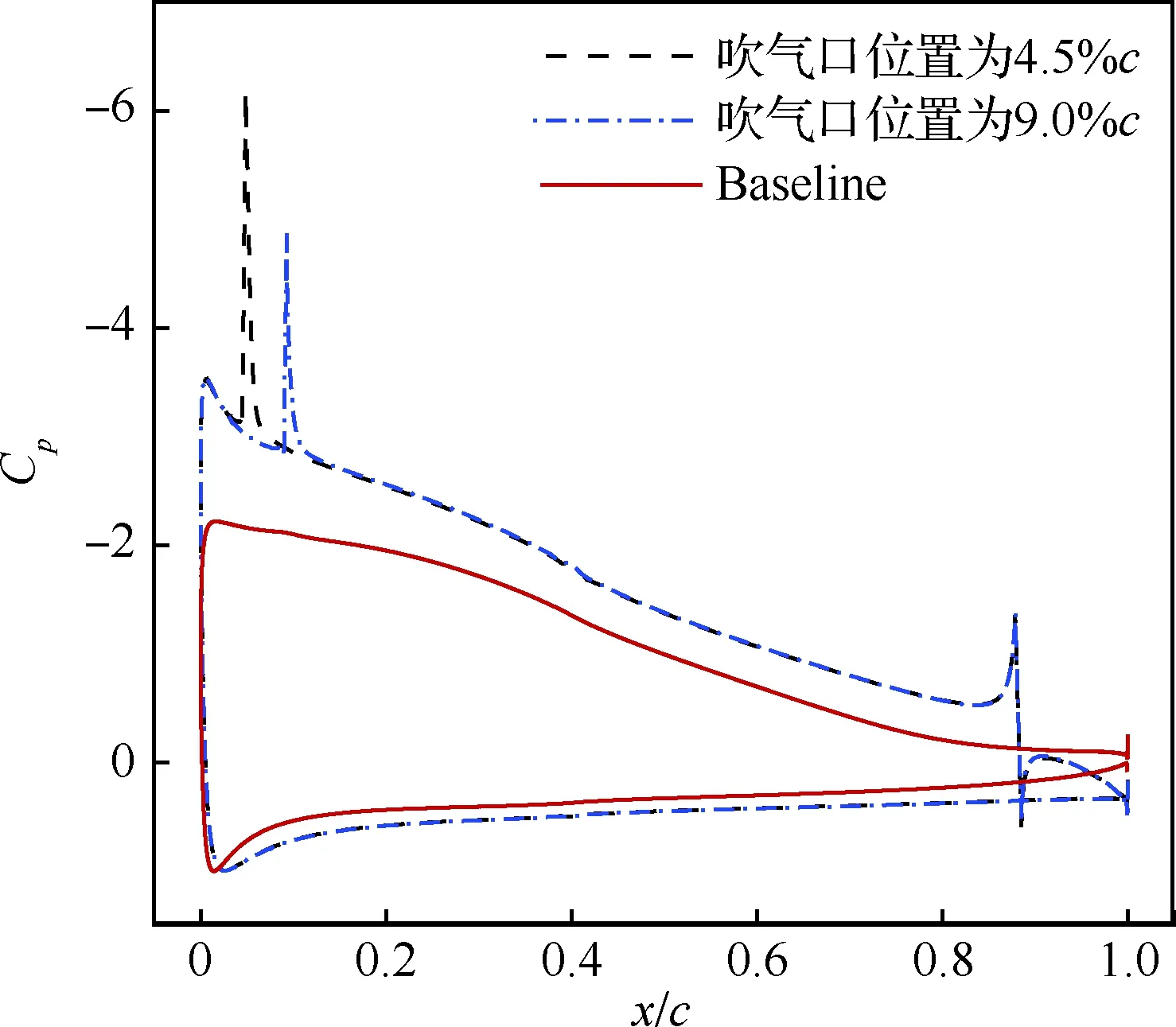
圖17 不同吹氣口位置的壓力系數分布對比(α=10°)Fig.17 Comparison of pressure coefficient distribution at different injection locations(α=10°)
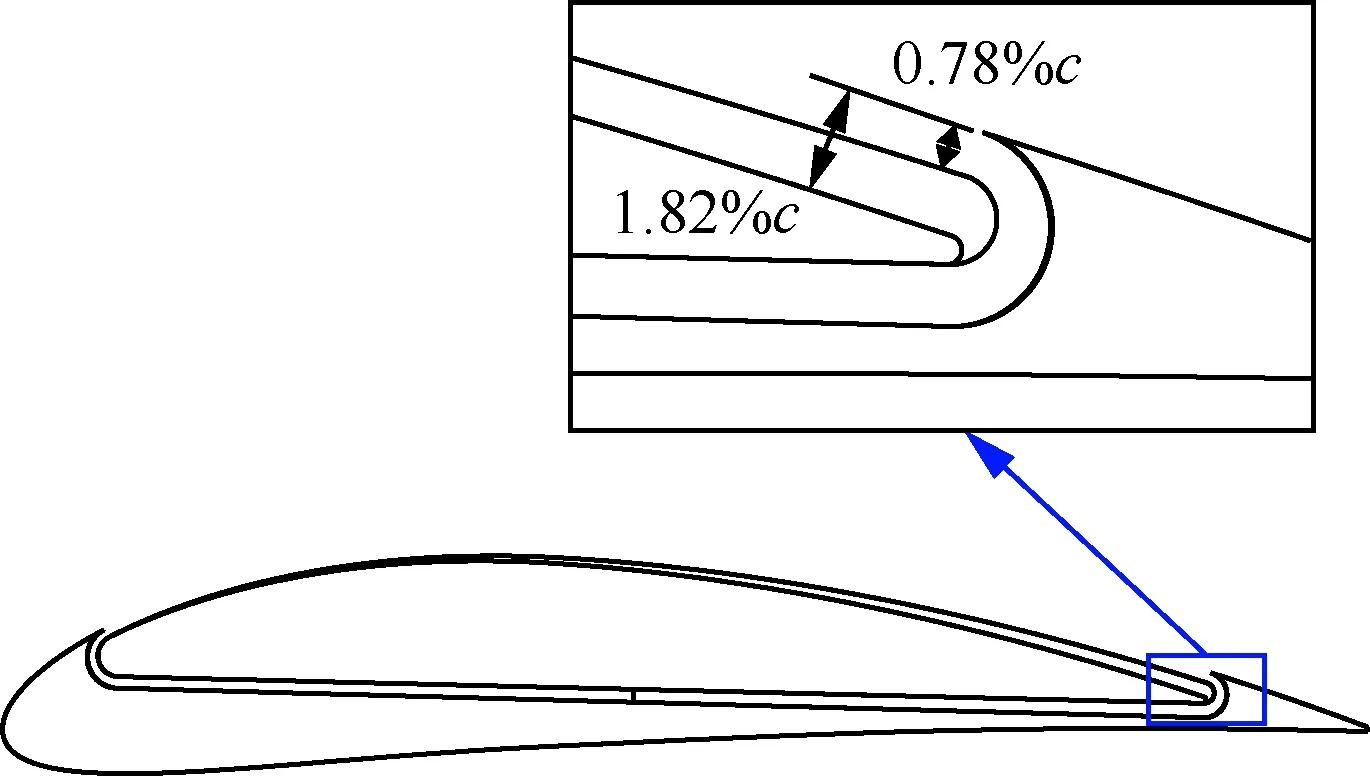
圖18 最小和最大吸氣口尺寸示意圖Fig.18 Sketch of minimum and maximum suction sizes
由圖19可知,隨著吸氣口尺寸增加,翼型的升力系數幾乎不變;有效阻力系數和氣泵功率系數逐漸減小;有效升阻比先增加,后趨于平穩。吸氣口尺寸較小時,氣動力變化相對較大,并且迎角越大,變化越明顯。
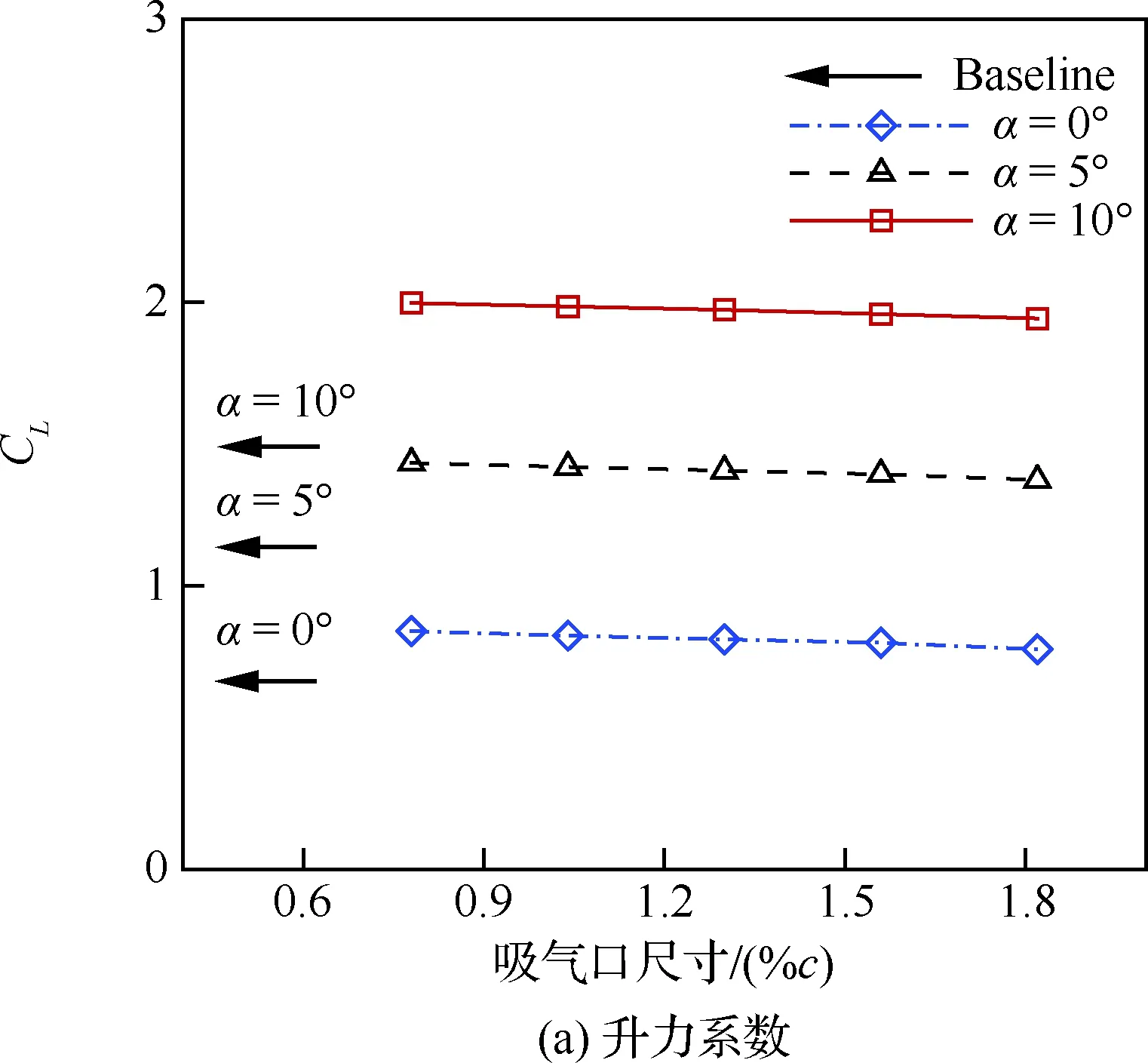
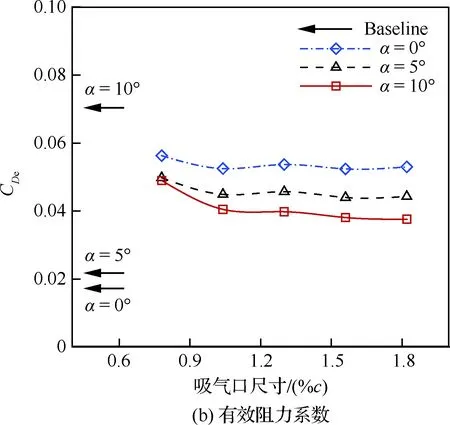
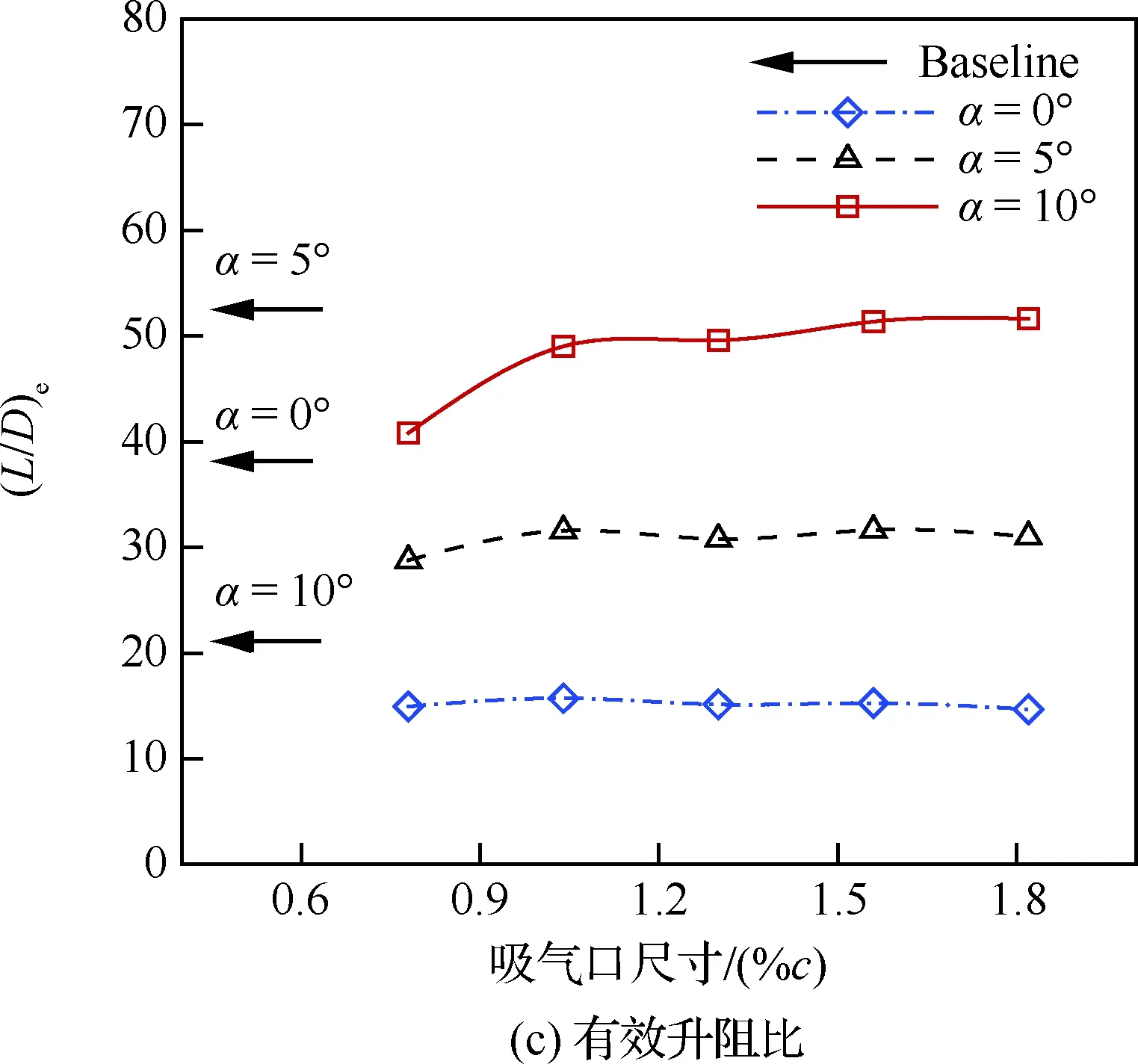
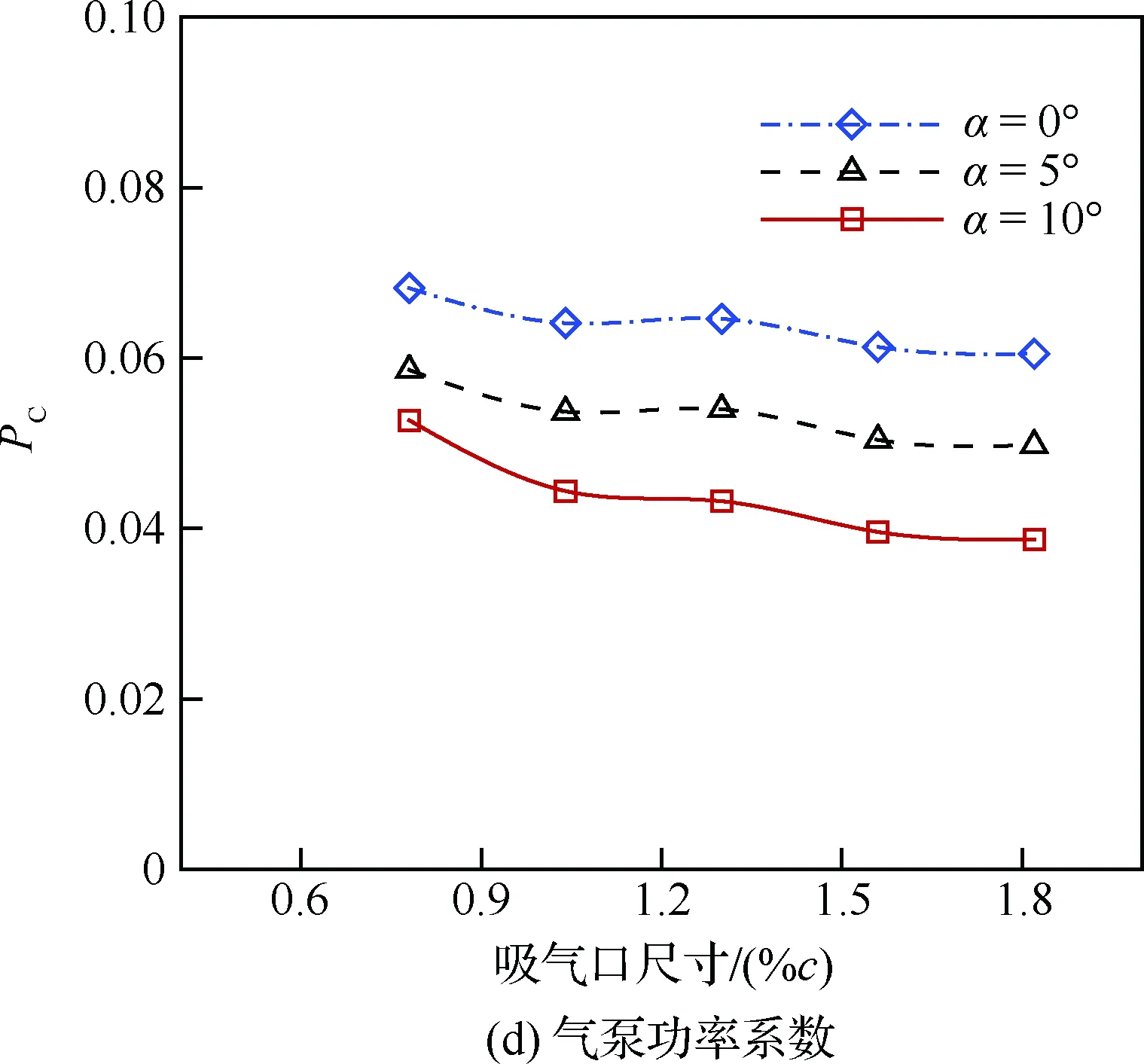
圖19 吸氣口尺寸對氣動性能的影響(Cμ=0.08)Fig.19 Effects of suction size on aerodynamic performance (Cμ=0.08)
圖20給出了10°迎角下,不同吸氣口尺寸的馬赫數云圖和流線圖,可以看出,吸氣口尺寸較小(0.78%c)時,雖然吸氣口處氣流速度較高,但是通過吸氣口管道截面的質量流量仍然無法維持與吹氣口相同的質量流量,因此必須從吸氣口上方吸入額外的氣流以彌補流量的不足,導致吸氣口內壁存在較大的分離流動,從而氣泵功率系數較大,相應的有效阻力系數也就更大;隨著吸氣口尺寸增加,“流量不平衡”的問題得以緩解,分離逐漸減小直至消失,氣泵功率系數也因此逐漸減小。
圖20 不同吸氣口尺寸的馬赫數云圖和流線圖(α=10°)Fig.20 Mach number contours and streamlines for different suction sizes(α=10°)
隨著吸氣口尺寸增加,吸氣口內壁存在的流動分離逐漸消失,流動發生了本質變化,這是吸氣口尺寸較小時氣動力變化相對較大的主要原因,因此為避免吸氣口內側出現分離流動,吸氣口尺寸不宜過小。
4.5 吸氣口位置的影響
保持其他參數不變,在迎角分別為0°、5°和10°時,研究了吸氣口位置對升力系數、有效阻力系數、有效升阻比和氣泵功率系數的影響規律及機理。吸氣口位置變化范圍為62.0%c~88.5%c,如圖21所示。
由圖22可知,吸氣口位置對翼型氣動力幾乎沒有影響,但隨著吸氣口位置向后移動,氣泵功率系數逐漸增加。圖23分別給出了迎角為10°時不同吸氣口位置的馬赫數云圖和流線圖,圖24給出了不同吸氣口位置的壓力系數分布。吸氣口位置越靠后,射流向主流輸送的能量越多,同時吸氣口處主流速度越低,因此氣泵加速氣流消耗能量越大,從而氣泵功率系數越大。
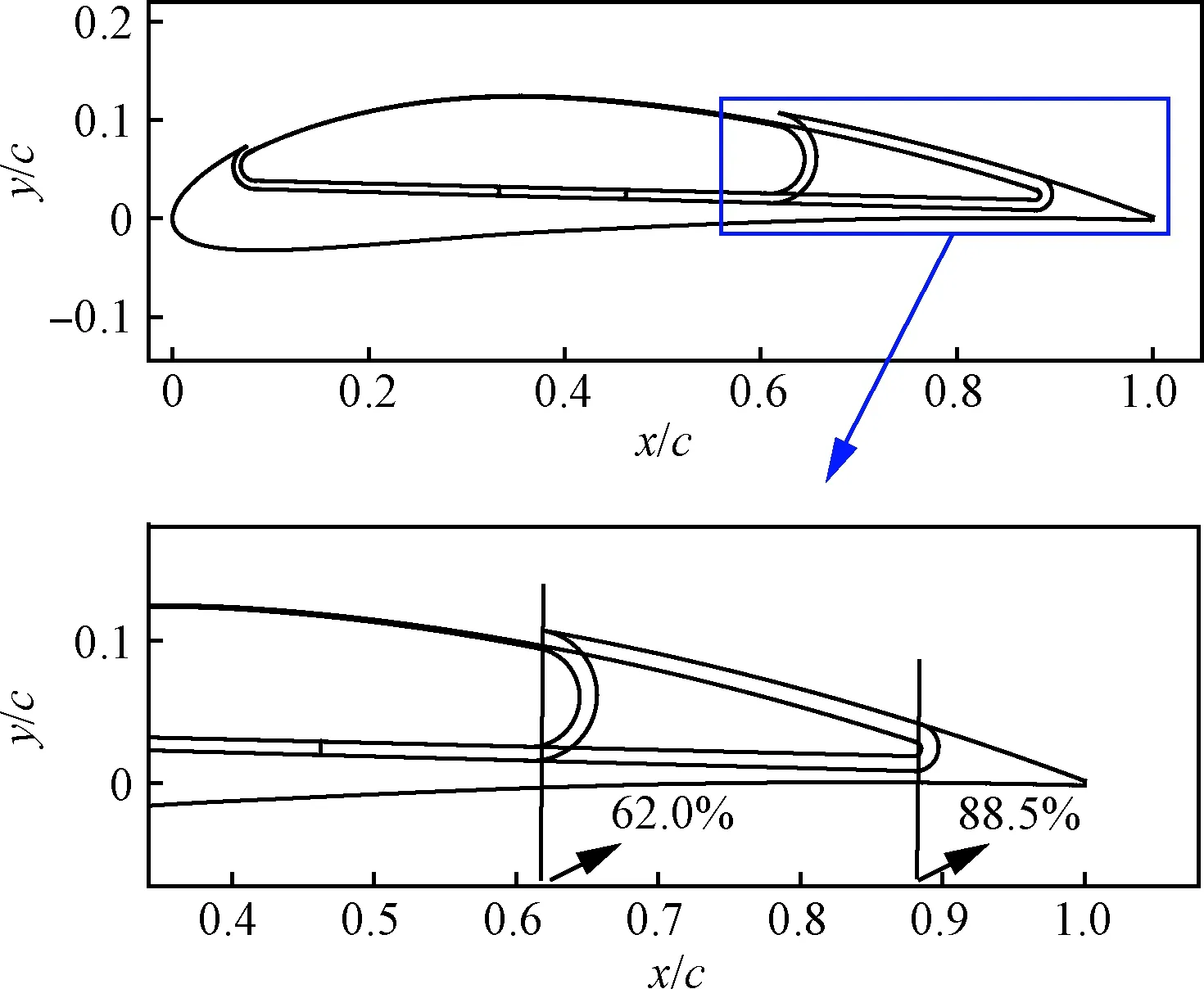
圖21 最小和最大吸氣口位置示意圖Fig.21 Sketch of minimum and maximum suction location
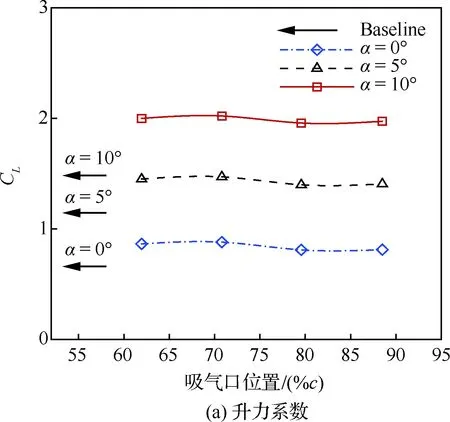

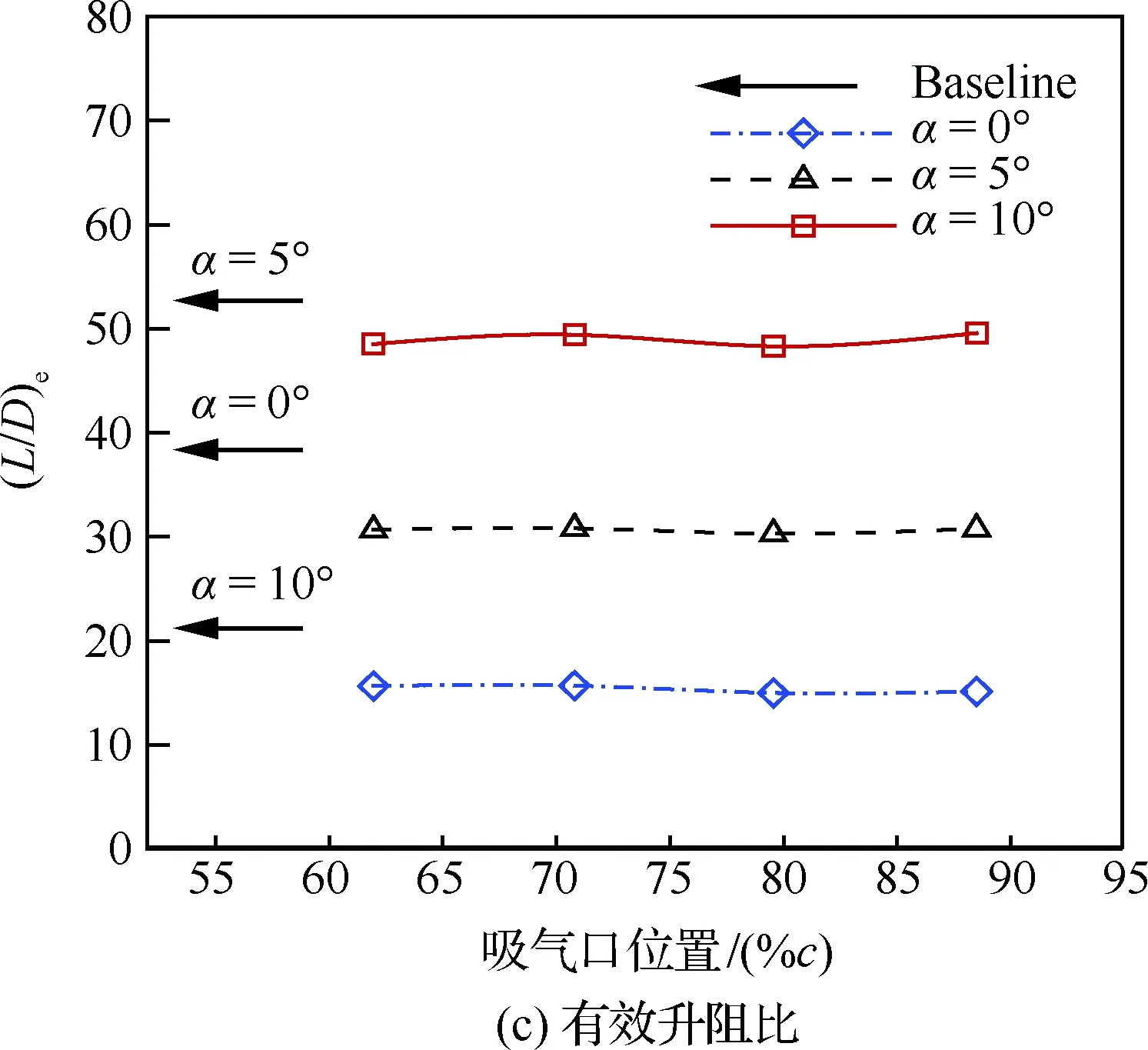
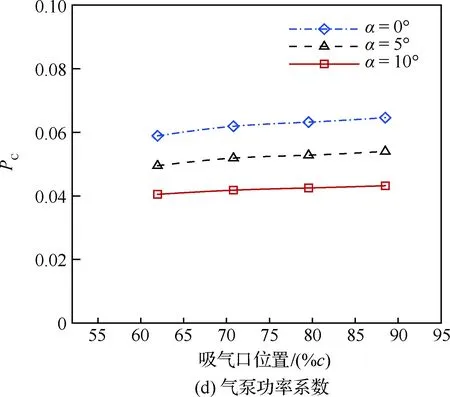
圖22 吸氣口位置對氣動性能的影響(Cμ=0.08)Fig.22 Effects of suction location on aerodynamic performance(Cμ=0.08)
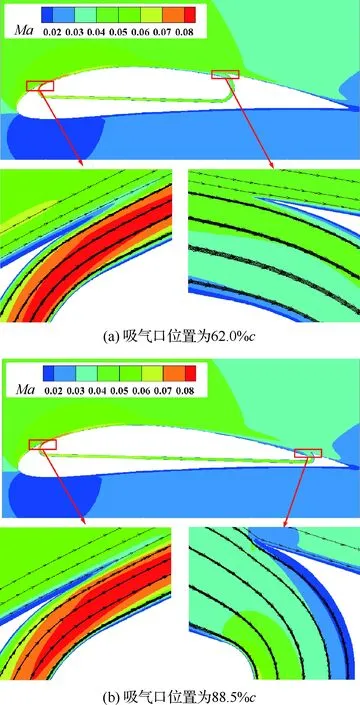
圖23 不同吸氣口位置的馬赫數云圖和 流線圖(α=10°)Fig.23 Mach number contours and streamlines at different suction locations (α=10°)

圖24 不同吸氣口位置的壓力系數分布對比(α=10°)Fig.24 Comparison of pressure coefficient distribution at different suction locations (α=10°)
5 結 論
1) 本文提出的基于激勵盤模型的協同射流翼型繞流數值模擬方法是有效的。
2) 隨著射流動量系數增加,有效升阻比先增后減,而氣泵功率系數的總體趨勢是增加的。最大有效升阻比對應的射流動量系數隨迎角增加而增大。大迎角狀態下,流動分離使得射流動量系數對翼型氣動性能的影響規律更加復雜。當流動分離被完全抑制后,影響規律與小迎角附著流動狀態相似。
3) 隨著吹氣口尺寸增加,升力系數幾乎不變,有效阻力系數和氣泵功率系數存在一個最小值,從而有效升阻比存在一個最大值,該最大值對應的吹氣口尺寸隨迎角增加而減小。
4) 隨著吸氣口尺寸增加,升力系數幾乎不變,有效阻力系數和氣泵功率系數逐漸減小,有效升阻比先增加,后很快趨于平穩。為避免吸氣口內壁出現分離,吸氣口尺寸應不小于1%c。
5) 吹氣口位置和吸氣口位置對翼型氣動性能和氣泵功率系數的影響較小。

