平板式催化劑裝箱過程中軌跡規劃的研究

許 超，鄒光明，王興東，王 黎

1 引言

高階軌跡規劃主要應用在工業機器人、精密機床、微機械等高精密設備中，與二階梯形速度曲線相比，其運動曲線更加平滑，穩定性大大增加，能夠使設備運動中的沖擊性和殘余振動極大地減小[1-2]。為實現對平板式催化劑裝箱效率的提升，改善工人工作狀況，降低工人的勞動強度，提高企業的自動化水平和節約其生產成本，因此設計了一種能夠使工人避免高強度、高密度作業的裝箱自動化設備。該設備包含板材定位裝置、搬運機器人裝置、自動換箱裝置、板材整平裝置。其搬運機器人采用成本低，可靠性高，模塊化程度高的直角坐標系機器人，x軸和z軸采用同步帶傳動方式，但考慮到帶傳動剛性略小[3]，屬于柔性件傳動，傳動部分的剛度大小與伺服控制系統的閉環共振頻率點息息相關，帶傳動很容易出現共振頻率點，從而導致機器人在工作過程中的定位和速度跟蹤有很大波動，且有可能出現振蕩情形，顯著增加機械噪音，頻繁的快速啟、停動作對機械結構的沖擊和磨損非常嚴重，為了能夠使平板式催化劑裝箱設備在裝箱過程中運動快速平穩，運動規劃對平板式催化劑裝箱作業顯得尤為重要。

梯形速度曲線運動主要是加速度突變產生無限大的瞬間沖擊量[4]，而高階軌跡曲線，不管是加速度工作過程還是其他時刻，其沖擊值始終是個非突變的數，原理上是高階運動軌跡過程把伴隨沖擊釋放的能量分散到加速時間段上，從而把對機器損傷程度降到最小。運動曲線階數越高[5]，速度曲線越光滑，但是輸入信號只能控制加速度和速度，加加速度是不可以控制的，只能用作計算，并且速度曲線越繁雜，就會拖慢系統的響應速度，所以在實際運用中，并不是速度曲線階數越高設備運行效果越好。因此裝箱設備中的搬運機器人和換箱裝置采取的是三階點對點運動控制模式，根據設備實物結構和工作環運動方式[6]，在傳統的點對點運動規劃的基礎上，提出了一種以時間最優為規劃目標的高精度點對點軌跡規劃方法以減少對機械結構的沖擊和殘余振動，并用于實際工程項目中，提高板式催化劑的裝箱效率。

2 裝箱設備工藝動作的分析

設計的平板式催化劑裝箱設備，如圖1所示。其板材搬運機器人為一種三自由度的直角坐標系機器人，因為平板式催化劑裝箱要求為連續的兩塊板要前后交錯排列、水平旋轉180°裝箱，因此該機器人包含水平方向平移運動、豎直方向上下運動和板材抓取吸盤的旋轉運動三個自由度。其運動可分為上升階段：機器人吸盤從傳送帶上的抓取位置吸起產品，上升到擋板的高度；到位階段：機器人從板材抓取位置上方移動到箱子平臺位置的上方；下降階段：機器人從箱子平臺位置上方下降到箱子平臺位置進行裝箱，其裝箱工作方向示意圖，如圖2所示。當箱子裝滿時，換箱裝置開始動作，將裝箱完成的換箱平臺移出工位，將空箱平臺移入工位，開始下一階段的裝箱過程。

圖1 平板式催化劑裝箱設備Fig.1 Plate Type Catalyst Packing Equipment

圖2 搬運機器人工作方向示意圖Fig.2 Working Direction of Handling Robot

3 高階軌跡規劃

平板式催化劑裝箱設備在工作中總是常常處于快速啟、停和速度較高的運動模式，其加、減速過程對機器設備的性能具有很大影響，容易激起殘余振動。要使得設備運行得更穩定、快速和定位更精確，則當它啟、停時需要保證速度運行曲線是平緩的[7]，而不應出現加速度突變，目前許多學者已提出了很多可行的軌跡規劃及光滑處理的方法，但這些方法一般會大大增加軌跡規劃的運動執行時間，影響設備運行效率，不利于向高階擴展。因此依照高階規劃的特點，提出了一種既能滿足給定速度，又能保證高階軌跡規劃運動最大參數值的一種三階軌跡規劃的控制算法，并根據軌跡的各自情況總結出其共同特征并推導其算法公式，描述了軌跡的全局預處理過程，實現了時間優化，并據此給出軌跡規劃[7]的實現流程。

平板式催化劑裝箱要求保證終點位置精度，點對點運動為兩點間的運動，通常會采用直線運動以實現運動的快速性，并且起止點對應的約束為零，三階點對點軌跡典型的對稱位置軌跡包含勻加加速段，勻加速段，勻速段[8]，軌跡曲線，如圖3所示。

圖3 典型三階點對點軌跡輪廓Fig.3 Typical 3 Order Point to Point Trajectory Profile

但若更改某些給定的約束條件，軌跡曲線將不含勻加速段或勻速段，即運動軌跡存在多種情形[9]，通過總結分析各種情況相應的特征約束，并對相關公式進行推導，概括總結出用來判別各種情況的準則，由此實現運動軌跡的精確規劃。加速度軌跡情形主要有以下幾種：（1）情形一、加速度為梯形且上下兩梯形不相連情形，如圖4（a）所示。此情形表示整個運行位移較大，最大加速度先達最大值后，最大速度的最大值先于位移到達，此時速度軌跡含有常速段。（2）情形二、加速度為梯形且上下兩梯形相連情形，如圖4（b）所示。此情形表示整個運行位移較大，最大加速度先達最大值后，最大速度的最大值先于位移到達，此時速度軌跡不含常速段。（3）情形三、加速度為三角形且上下兩三角形不相連情形如圖4（c）所示。此情形表示整個運行位移較大、但速度小或者是運行位移小、但速度更小，在速度滿足的情況下，加速度還沒到達最大值，運動位移還未滿足，此時速度軌跡含有常速段。（4）情形四加速度為三角形且上下兩三角形相連情形，如圖4（d）所示。此情形表示整個運行位移小、速度大或者是速度小位移更小，在速度和加速度都未滿足的情況下，位移已到最大值，此時速度軌跡不含常速段。

圖4 四種加速度軌跡情形Fig.4 Four Kinds of Acceleration Trajectories

4 三階軌跡規劃算法

三階軌跡公式推導和算法實現：這里給定加加速度常數h，最大加速度amax，最大速度vmax，位移s。為使算法對以上四種情形都適用，故將以上四種情形都按加速度為梯形且上下兩梯形不相連處理。因此，三階軌跡運行時間被劃分為7個時間段t1-t7，7個時間段對應的時間點為：

軌跡規劃的加加速度為位移對時間的三階導數，為速度對對時間的二階導數，為加速度對時間的一階導數，軌跡規劃的數據通過積分進行計算，其計算公式，如式（1）所示。

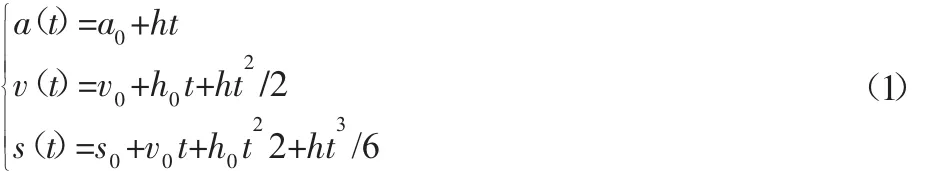
但如果采用上述積分公式對各個時間段求解，要解大量的方程式，大大增加了計算量，因此我們在計算中不采用此方法，而采用工程中運用的面積分割法來對各時間段求解，這樣就極大的簡化了推導過程，體現了工程應用中直接、簡單的要求。面積分割法步驟如下，根據圖4，加加速度動作的時間為t1，勻加速時間段為t2，勻速時間段t4，確定了這三個參數后，再根據軌跡的對稱性計算出整個軌跡的時間。在t′1時間點上加速度 a（t′1）的大小為加加速度h在時間t1段上的矩形面積，即a（t′1）=ht。在 t′3時間點上速度v3的值等于圖中加速度在前3個時間段圍成的梯形面積，v3=a（t′1）（t1+t2），整個位移的大小等于速度v在7個時間段上面積的總和，即s=v3（t1+t2+t3+t4）。由式（1）可以看出對三階公式的求解就是求解加加速時間段、加速度時間段和勻速時間段，這三個參數確定后就可確定整個軌跡的運行時間。推導各時間段時間，參考基準先按極端情況考慮，即可分為兩組情形，第一種是恰好達到最大加速度，并以最快的對稱軌跡方式使速度和加速度為0，此時的速度和位移記為va和sa，計算公式為

第二種是速度達到最大值，并以最快的對稱軌跡方式使速度和加速度為0。若加速度在速度前達到最大值，則此時的位移記為 sv1，計算公式為

若加速度在速度前未達到最大值，則此時的位移記為sv2，計算公式為

（1）當s≥sv2且vmax≥va時，此時加速度軌跡包含七段，形狀為梯形不相連的情形，最大加加速時間t1由加速度確定：

由軌跡對稱性可知t1=t3=t5=t7。勻加速時間段為：

由軌跡對稱性可知t2=t6。勻速時間段為：

（2）當 s≥sv2且 vmax＜va時，此加速度軌跡包含五段，形狀為三角形不相連的情形，最大加加速時間t1由速度確定：

由軌跡對稱性可知t1=t3=t5=t7。勻加速時間段為：t2=t6=0。

（3）當s≥sa且s≤sv2時，此時加速度軌跡包含六段，形狀為梯形相連情形，此時可達到的速度為：

則最大加加速時間t1由加速度確定：t1=amax/h （11）

由軌跡對稱性可知t1=t3=t5=t7；

勻加速時間段為：t2=（vmaxsub-a2max/h）/amax（12）

由軌跡對稱性可知t2=t6；勻速時間段為：t4=0。

（4）當 sv1≤s≤sa且 vmax＜va時，此加速度軌跡包含五段，形狀為三角形不相連的情形，最大加加速時間t1由速度確定：

由軌跡對稱性可知t1=t3=t5=t7；

勻加速時間段為：t2=t6=0；

（5）當 s≤sa且 vmax＞va或 s≤sa且 s＜sv1時，此加速度軌跡包含四段，形狀為三角形相連的情形，此時加速度最大值為：

最大加加速時間t1由速度確定：t1=amaxsub/h （16）

由軌跡對稱性可知t1=t3=t5=t7；勻加速時間段為：t2=t6=0；勻速時間段為：t4=0。

經過以上過程，已求出加加速度時間段，勻加速度時間段和勻速時間段，相應的軌跡公式如下：

在t7時間段：

由于計算機在運算中會省略一部分浮點運算，會使計算精度降低，因此對此軌跡必須進行離散化處理和圓整化處理。

5 仿真及結果分析

本催化劑裝箱設備的搬運機器人沿著x軸的位移需根據不同尺寸的催化劑板進行調整，其位移區間為（1.3～2）m，下面列出幾組不同約束條件下的仿真結果，給定其約束參數如表1中參數一～參數四所示。

從表1可知：參數一可達到給定速度和加速度，所需總時間為4.1333s，勻加加速時間為0.3s，運動曲線有七個階段組成，運動曲線，如圖5（a）所示；參數二達到的最大速度為0.79m/s，所需總時間為3.2592s，勻加加速時間為0.3s，運動曲線有六個階段組成，不含勻速段，運動曲線，如圖5（b）所示；參數三可達到的最大加速度為0.8944m/s2，所需總時間為4.2s，勻加加速時間為0.8944s，運動曲線有五個階段組成，不含勻加速段，運動曲線，如圖5（c）所示；參數四可達到最大速度為0.7504m/s，最大加速度為0.8662m/s2，所需總時間為3.4649s，勻加加速時間為0.8662s，運動曲線有四個階段，不含勻加速和勻速段，運動曲線，如圖5（d）所示。

表1 給定的各組參數及其計算結果數據Tab.1 Given Parameters of Each Group and Calculation Result Data

通過對比多次仿真結果可知：（1）在給定加加速度的情況下，由于運行位移的距離不同導致加加速時間段不同，加速度和速度達到的最大值也不相等；由于給定速度或給定加速度不同得到的加速段時間也就不同，運行的總時間也有差別，給定速度越大，所需總時間越短；（2）當改變給定加加速度的情況下，給定加加速度越小，運行總時間越長。

6 結論

選用高階軌跡對設備中搬運機器人運動軌跡進行了規劃，在傳統的點對點運動規劃的基礎上，提出了以時間順序推導的一種以時間最優為規劃目標的高精度三階點對點軌跡規劃算法，即先求出滿足各個約束的時間參數，然后將各約束用時間參數表達后反向推導，最后得到軌跡規劃算法，并針對設備運行位移長度的差別，進一步選出幾組參數給出了仿真驗證，驗證了此算法可以確保加速度和速度均連續變化，該算法計算量小，較易實現編程控制，算法對控制器要求不高，可大幅節約成本，對精度有高要求的直線運動設備有很大的借鑒價值。經過試驗驗證，對催化劑板材搬運過程的高精度軌跡運動優化后，提高了其定位精度，并且減少了對機械結構的沖擊和殘余振動，運行平穩，裝箱效率大幅提高，取得了預期的效果。

圖5 幾組參數對應的運動曲線圖Fig.5 Several Corresponding Motion Curve of Set Parameters