直列四缸發動機曲軸扭轉振動固有特性分析

張洪飛，閆守成

1 引言

曲軸扭轉固有特性分析是扭振減振器設計的基礎，當前較成熟分析方法包括基于有限元模型和基于集總參數模型兩種模態分析法。前者為簡化處理，將無限個自由度實體模型經單元網格劃分簡化成有限個自由度有限元模型，是實際結構和物質數學表示方法，有限元分析方法是目前工程分析的主要方法[1]。后者實際形態很復雜，每個軸段都是即有慣量又有彈性振動體，這樣數學模型無法處理。依照經典振動理論，按照振動特性不變原則，將一個實際曲軸簡化成可進行數學運算理想系統，假設曲軸只有轉動慣量無彈性變形的一些集中質量和一些只有彈性而無轉動慣量的彈性軸段組成。

對扭轉振動研究：文獻[2]搭建發動機曲軸平面模型，采用傳遞矩陣法獲得曲軸扭轉振動和彎曲振動解；文獻[3]搭建曲軸三維空間模型，采用傳遞矩陣法獲得曲軸扭轉振動、軸向振動和兩個橫向振動的解；文獻[4]分析基于實模態靈敏度分析結構動力學修改原理用于扭振控制；文獻[5]搭建試驗臺對比安裝與否減振效果進行對比，提出減振措施。

以某四缸汽油發動機曲軸軸系為例，分別用基于有限元模型和集總參數模型模態分析法計算曲軸軸系扭轉固有特性。同時明確基于有限元及集總參數模型進行曲軸扭轉固有特性分析關鍵點，基于完整曲軸有限元模型，特別是活塞連桿機構的幾種等效方法以及集總參數模型中曲軸各段扭轉剛度的有限元全模型計算方法。對兩種方法獲得曲軸的扭轉固有頻率進行對比。

2 曲軸軸系有限元模型模態分析

2.1 曲軸有限元模型

應用Pro/Engineer中建立某款直列四缸汽油機曲軸模型，導入ANSYS建立有限元模型，進行模態分析和各軸段扭轉剛度求解。在建立有限元模型前要對曲軸的三維實體數字模型進行簡化，將活塞連桿組以及飛輪總成等結構刪除，在模態分析中用Mass點代替[6]。曲軸軸系相關參數，如表1、表2及圖1所示。

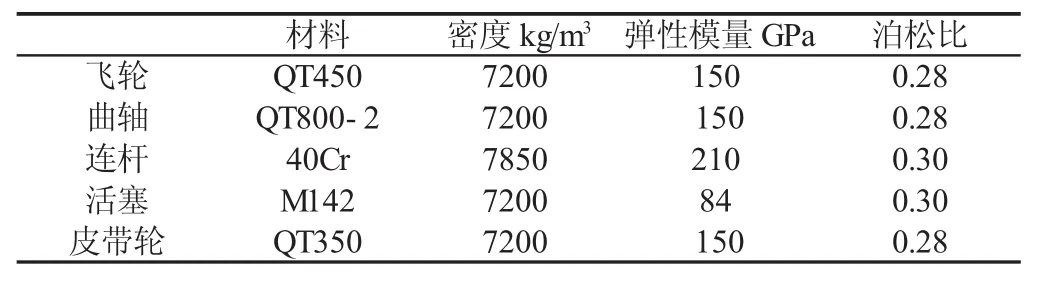
表1 曲軸軸系的材料參數Tab.1 Material Parameters of Crankshaft System

表2 曲軸軸系的相關參數Tab.2 Parameters of Crankshaft System（質量 m/kg，轉動慣量 I/kg·m2，長度 /mm）

圖1 簡化后的曲軸軸系Fig.1 Simplified Crankshaft System

為便于計算截面扭轉角度，預先將曲軸橫向切分為若干段，各截面，如圖2所示。截面1為曲軸上皮帶輪輪轂鍵槽橫向中央截面，截面 2、4、6、8、10 為主軸頸中央截面，截面 3、5、7、9 為連桿軸頸中央截面，截面11為曲軸與飛輪的接觸面。

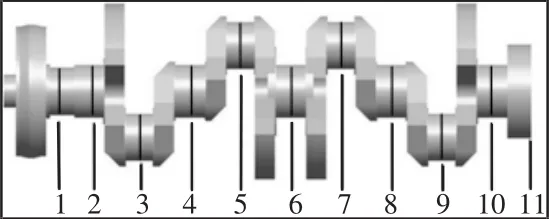
圖2 曲軸分段示意圖Fig.2 Schematic Diagram of the Crankshaft

采用8節點Solid45單元，對主軸頸和曲柄軸頸用精度為1網格劃分；平衡塊和曲拐部分用精度為3網格劃分，共得到48794個節點，如圖3所示。

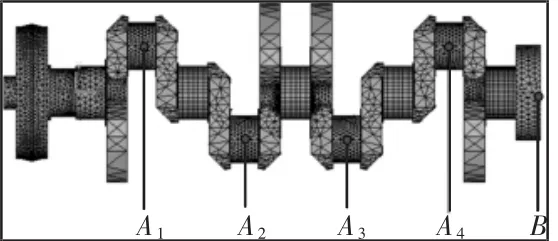
圖3 曲軸軸系有限元模型Fig.3 Finite Element Model of Crankshaft System

將所有節點坐標轉換為以曲軸中心線（z軸）為軸線柱坐標，便于后續施加轉矩載荷和徑向約束。將活塞連桿組、飛輪總成等效為相應集中質量或轉動慣量；在圖3中A1～A4、B等硬點所生成節點上創建相應等效Mass單元。將各Mass單元與其附近節點形成一剛性區域，確保Mass單元等效集中質量和轉動慣量正常參與曲軸動力學行為[7]。

2.2 模態分析

在有限元模型基礎上，施加約束，進行軸系扭轉振動模態分析。實際運行時受主軸承對曲軸主軸頸支撐作用。軸系扭轉固有頻率遠小于彎曲固有頻率，在分析扭轉固有特性時可對有限元模型進行簡化。由于只分析扭轉固有特性，將每個主軸頸徑向施加約束，既能略去其他模態，又能得到準確的扭轉固有頻率[8]。

采用ANSYS中模態分析法，分析1 Hz以上（以濾去剛體轉動模態）5階模態。所分析四缸汽油發動機曲軸系第一、二階扭轉模態頻率分別為477 Hz、1214 Hz。其中，第一階扭轉模態節點在飛輪前端的主軸頸上并靠近飛輪，陣型正常。

3 集總參數模型模態分析

3.1 集總參數模型

直列四缸發動機曲軸簡化成六自由度當量軸盤系統，當量盤只包含轉動慣量不包含剛度，當量軸只提供剛度不包含轉動慣量。以各軸頸中央截面為界將軸系劃分成若干段，每一段用一個集中轉動慣量代替連續體轉動慣量[9]。剛度即是每個連續質量之間實際剛度，集總參數模型各質量塊轉動慣量和各質量塊之間剛度轉化，如圖4所示。以圖4（a）所示各主軸頸中央截面為界將軸系劃分成六段，各段轉動慣量對應圖 4（b）所示 I1～I6。圖 4（b）所示各自由度之間扭轉剛度 K1～K5分別為圖 3 中截面 1～3、3～5、5～7、7～9、9～11 之間曲軸軸段的扭轉剛度。

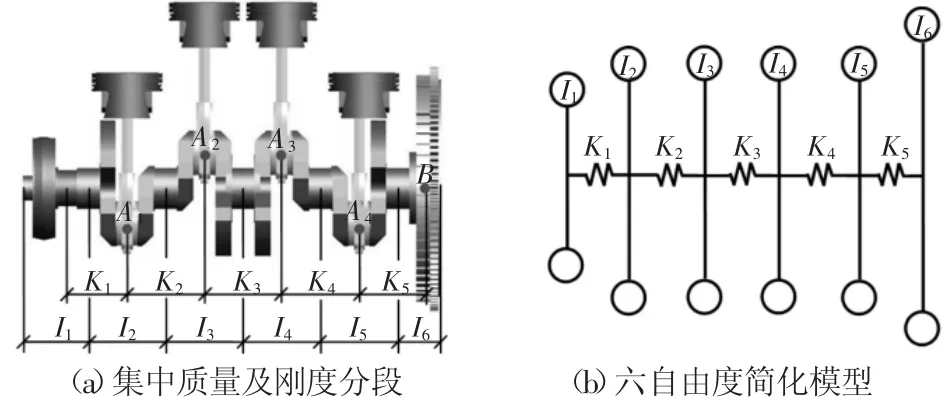
圖4 多自由度集總參數模型的簡化Fig.4 Simplification of the Lumped Parameter Model

曲軸六自由度簡化模型，自由振動矩陣方程：

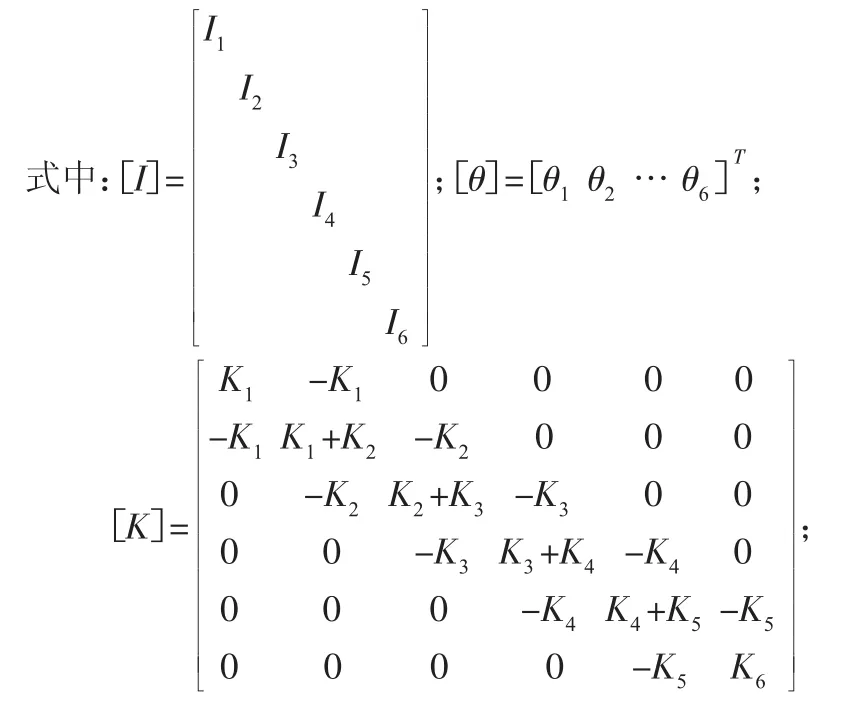
求解式（1）關鍵在于集總參數模型中轉動慣量與扭轉剛度計算。

3.2 轉動慣量計算

式中：d m—微質量；r—微質量到回轉半徑距離；m—物體的總質量。

基于有限元模型求得各零件轉動慣量，曲軸各段質量塊模型，如圖5所示。

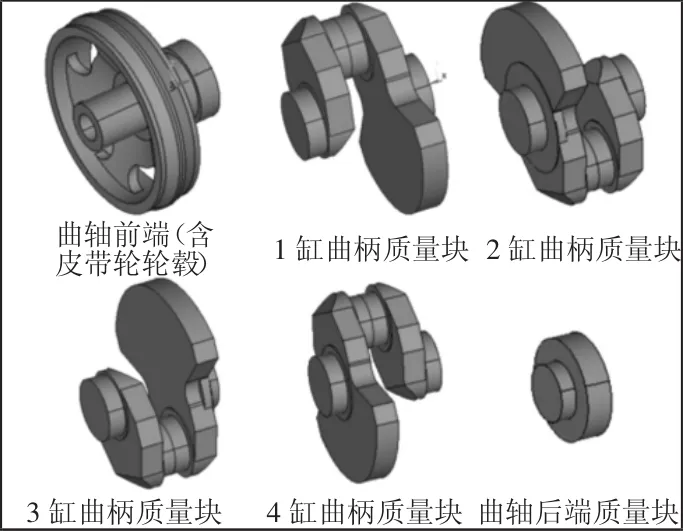
圖5 各質量塊模型Fig.5 Each Mass Block Model

計算得到曲軸各軸段轉動慣量，如表3所示。

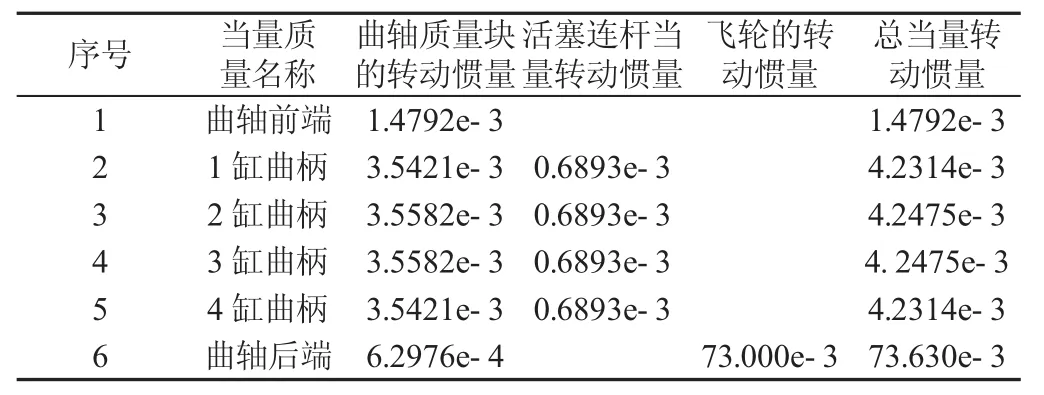
表3 曲軸軸系的當量轉動慣量Tab.3 Equivalent Moment of Inertia of Crankshaft（轉動慣量 I/10-3kg·m2）

3.3 扭轉剛度計算

軸段扭轉剛度：扭轉軸段使其旋轉單位角度（1rad）時所需要的扭矩[10]，則：

式中：M—扭矩；Δφ—軸兩端相對扭轉角度；G—軸段材料剪切彈性模量；Jp—截面極慣性矩；L—軸段長度。

曲軸各軸段扭轉剛度是一個很難確定參數，可采用經驗公式進行推算，如西馬年科公式、卡特公式，如式（4）、式（5）所示。

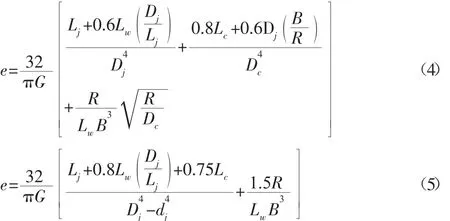
采用直接法和間接法兩種方法計算曲軸各軸段扭轉剛度。如圖2曲軸分段，直接法為計算曲柄軸頸中央截面3、5、7、9及1、11 截面轉角，直接得到 1～3、3～5、5～7、7～9、9～11 軸段兩端截面相對轉角，進而得到相應軸段扭轉剛度；間接法為計算主軸頸中央截面 2、4、6、8、10 及 1、11 截面轉角，分別求得 1～2、2～4、4～6、6～8、8～10、10～11軸段兩端截面相對轉角，進而得到相應軸段扭轉剛度，由于平衡塊對扭轉剛度影響可忽略，且 2～4、4～6、6～8、8～10軸段分別關于3、5、7、9截面對稱，按照剛度串聯法求得2～3、3～4、4～5、5～6、6～7、7～8、8～9、9～10 軸段扭轉剛度，再將相關軸段串聯得到 1～3、3～5、5～7、7～9、9～11 軸段扭轉剛度。直接法扭轉剛度求解，如表4所示。間接法求解，如表5所示。

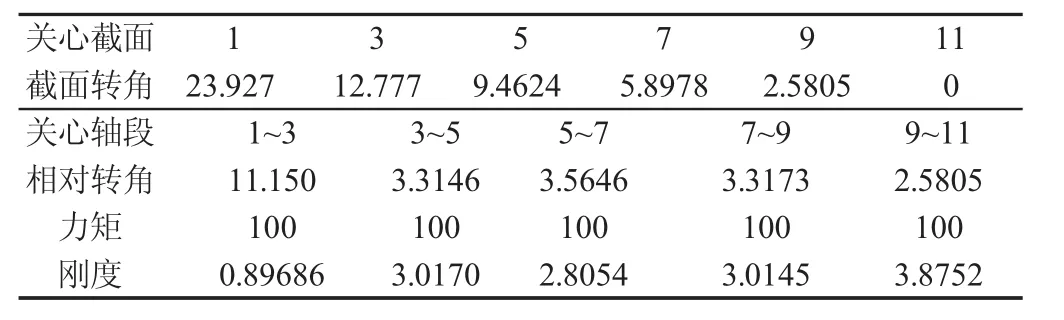
表4 直接法計算曲軸軸段扭轉剛度Tab.4 Calculation of Torsional Stiffness of Crankshaft by Direct Method（轉角θ/e-4rad，力矩 M/N·m，剛度K/105N·m·rad-1）

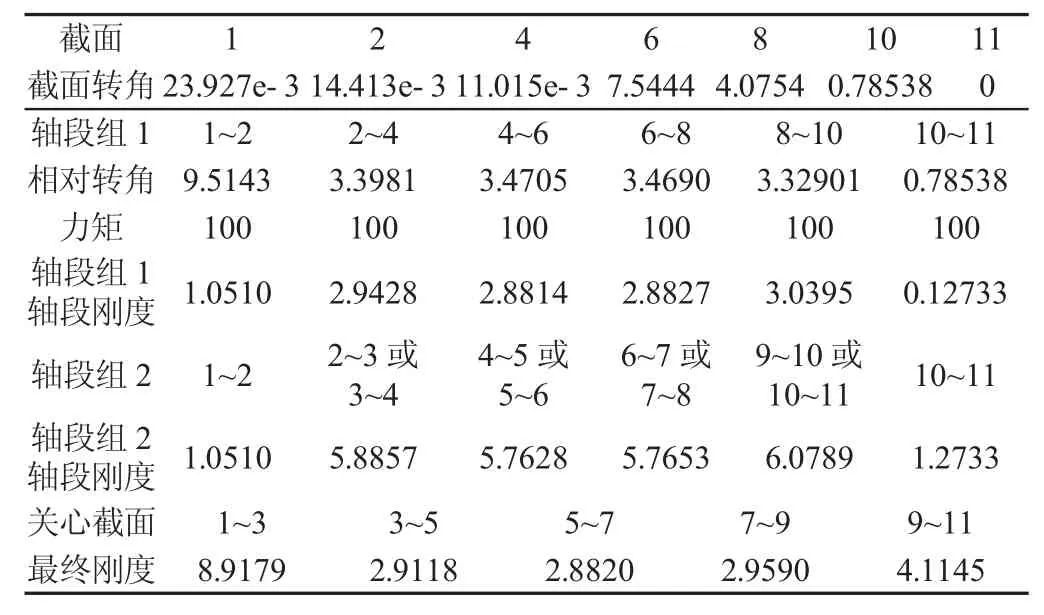
表5 間接法計算曲軸軸段扭轉剛度Tab.5 Calculation of Torsional Stiffness of Crankshaft by Indirect Method（轉角θ/e-4rad，力矩 M/N·m，剛度K/105N·m·rad-1）

兩種方法扭轉剛度對比，如表6所示。各軸段扭轉剛度相對誤差均在6%以內，具有很好吻合性。

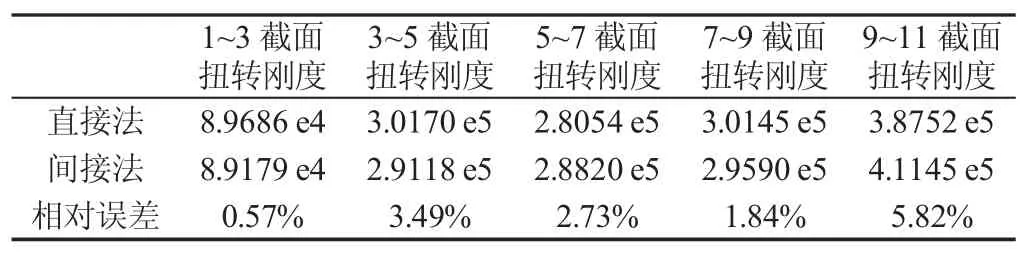
表6 直接法與間接法扭轉剛度計算結果對比Tab.6 Comparison of Direct and Indirect Methods（剛度 K/105N·m·rad-1）

3.4 集總參數模型求解

設式（1）特解形式為：

則求解式（1）轉換成求矩陣I-1K-λE的特征向量與特征值問題。

通過計算得到集總參數模型轉動慣量參數和各軸段扭轉剛度參數，用MATLAB進行矩陣I-1K-λE特征值與特征向量運算，即得集總參數模型中各階次扭轉模態頻率和相應階次陣型結果。基于直接法與間接法剛度計算集總參數模型前二階扭轉模態頻率，如表7所示。

表7 基于兩種算法集總參數模型模態頻率Tab.7 Modal Frequency

由表7可知，基于直接法與間接法剛度計算集總參數模型前二階扭轉模態頻率相差很小，均在3%以內，特別是兩種方法扭轉一階模態頻率誤差僅為0.621%，證明兩種剛度計算方法吻合性。

由于直接法剛度集總參數模型無任何假設條件，取該方法結果為最終集總參數模型模態分析結果，集總參數模型各質量塊相對振幅，如表8所示。陣型，如圖6所示。

表8 集總參數模型各質量塊相對振幅Tab.8 Relative Amplitude of Each Mass

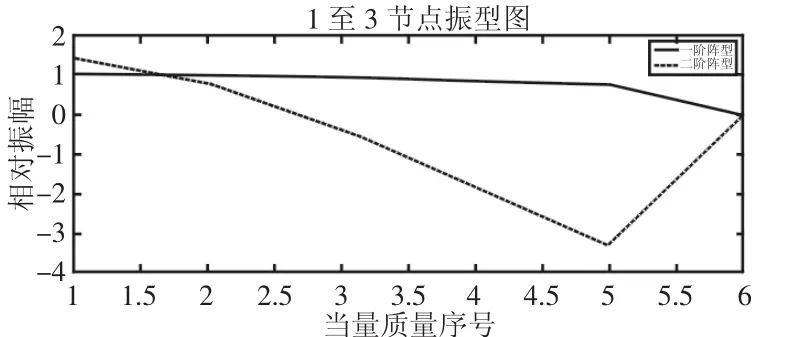
圖6 集總參數模型振型圖Fig.6 Vibration Pattern

4 曲軸扭轉固有特性對比

分別采用有限元模型與集總參數模型模態分析方法結果對比，如表9所示。

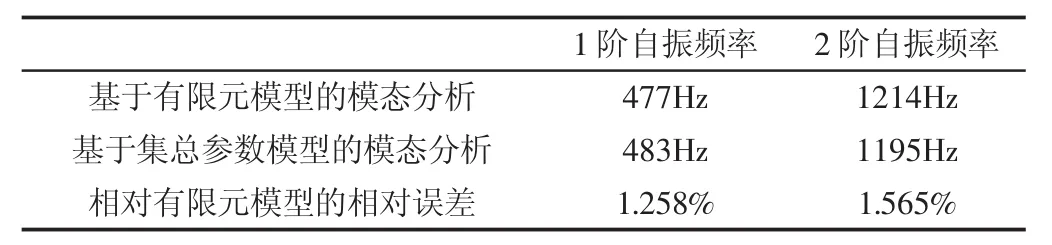
表9 扭轉固有特性分析方法結果對比Tab.9 Comparison of Analytical Results

由表9可知，兩種分析方法結果相對誤差僅在2%以內，基于集總參數模型與有限元模型的扭轉固有特性分析結果完全一致，兩種分析方法是統一的。

5 結論

對某四缸汽油發動機曲軸同時建立有限元模型和集總參數模型，分別計算曲軸扭轉固有頻率，對集總參數模型中曲軸各段扭轉剛度計算方法進行分析。結果表明：

（1）基于連桿軸頸中央截面分段直接剛度計算法和基于連桿軸頸和主軸頸中央截面分段然后串聯間接法兩種途徑計算曲軸各段扭轉剛度一致性好，精度滿足工程要求；前二階扭轉模態頻率相差很小，均在3%以內。

（2）基于集總參數模型與有限元模型的扭轉固有特性分析結果完全一致，兩種分析方法結果相對誤差僅在2%以內，兩種方法是統一的。

（3）兩種分析方法及結果一致性，為同類設計研究及扭轉減振研究提供可靠固有特性分析方法。