橋式起重機(jī)吊重Fuzzy-LQR防擺控制器的設(shè)計(jì)

李 軍，李學(xué)鋆

1 引言

起重機(jī)使用柔性繩索起吊重物使得結(jié)構(gòu)輕便，提高了作業(yè)效率，但存在很大的安全隱患和控制問(wèn)題。為了推進(jìn)起重機(jī)吊具的自動(dòng)化控制和智能化控制，對(duì)起重機(jī)吊具的防擺定位控制進(jìn)行研究具有十分重要的意義[1]。針對(duì)起重機(jī)吊重防擺定位出現(xiàn)了PID控制、最優(yōu)控制、滑模控制、模糊控制、神經(jīng)網(wǎng)絡(luò)控制、反步控制和無(wú)源控制等控制方法。由于起重機(jī)吊重的非線性特性，單一的起重機(jī)吊重防擺定位控制方式存在各種不足，因此利用多種控制方法相結(jié)合，實(shí)現(xiàn)優(yōu)勢(shì)互補(bǔ)，可以彌補(bǔ)不足，提高控制精度和控制反應(yīng)速度。文獻(xiàn)[2]建立了橋式起重機(jī)三維二自由度動(dòng)力學(xué)模型、傳遞函數(shù)及建立仿真模型并通過(guò)解耦的處理方式利用小車(chē)控制吊重?cái)[角，這種方式不僅可以快速控制擺角而且可以保證起重機(jī)定位。最后實(shí)驗(yàn)仿真驗(yàn)證該方法可行，但存在抖振和嚴(yán)重超調(diào)。文獻(xiàn)[3]根據(jù)拉格朗日方程建立了二維門(mén)式起重機(jī)動(dòng)力學(xué)模型及狀態(tài)方程，利用LQR控制方法對(duì)起重機(jī)吊重?cái)[動(dòng)進(jìn)行控制，仿真結(jié)果表明，給定輸入的情況下，擺角可以在10s的時(shí)間保持相對(duì)穩(wěn)定。文獻(xiàn)[4]人建立了起重機(jī)吊重三維模型和動(dòng)力學(xué)方程，并在x、y兩方向?qū)Υ笮≤?chē)進(jìn)行解耦，并對(duì)小車(chē)進(jìn)行了控制仿真。文獻(xiàn)[5]通過(guò)找出偏差和偏差變化率與PID控制器3個(gè)參數(shù)之間的模糊關(guān)系，完成了吊重?cái)[角的模糊PID控制設(shè)計(jì)。仿真結(jié)果證明了該方法的可行性且系統(tǒng)有較好的魯棒性，系統(tǒng)在外界干擾的情況下30s內(nèi)基本達(dá)到穩(wěn)定。文獻(xiàn)[6]建立了龍門(mén)吊車(chē)吊重二維動(dòng)力學(xué)模型，運(yùn)用魯棒控制理論分析設(shè)計(jì)出了一個(gè)雙閉環(huán)的PID控制系統(tǒng)。仿真結(jié)果表明其具有較好的穩(wěn)定性能，調(diào)節(jié)速度很快，但超調(diào)量大。通過(guò)建立橋式起重機(jī)吊重三維動(dòng)力學(xué)模型，并將大小車(chē)的運(yùn)動(dòng)狀態(tài)進(jìn)行解耦，通過(guò)信息融合將LQR控制的四個(gè)反饋量融合成模糊控制器的兩個(gè)輸入量，解決了模糊規(guī)則爆炸問(wèn)題，實(shí)現(xiàn)了fuzzy—LQR對(duì)起橋式重機(jī)吊重?cái)[動(dòng)的控制。

2 橋式起重機(jī)三維動(dòng)力學(xué)模型

橋式起重機(jī)是一個(gè)復(fù)雜的非線性系統(tǒng)，其系統(tǒng)狀態(tài)不僅與自身結(jié)構(gòu)和運(yùn)行狀態(tài)有關(guān)，還與系統(tǒng)所處環(huán)境有關(guān)，如所受風(fēng)力影響等。為了研究方便，建立橋式起重機(jī)吊具及重物的三維簡(jiǎn)化模型[7]，如圖1所示。為了使數(shù)學(xué)模型簡(jiǎn)化，對(duì)三維簡(jiǎn)化模型做以下簡(jiǎn)化：

（1）忽略摩擦力變化影響。（2）忽略繩索重量以及受力變形量。（3）忽略外界因素的影響。（4）對(duì)于一般不超過(guò)10°的小擺角，作近似處理，sinα≈α，sinβ≈β，cosα≈1，cosβ≈1，sinα·sinβ≈0，α˙2≈0，β˙2≈0，α˙β˙≈0。此外，選取 CXTD16t-19.5m 雙梁橋式起重機(jī)，其參數(shù)，如表1所示。

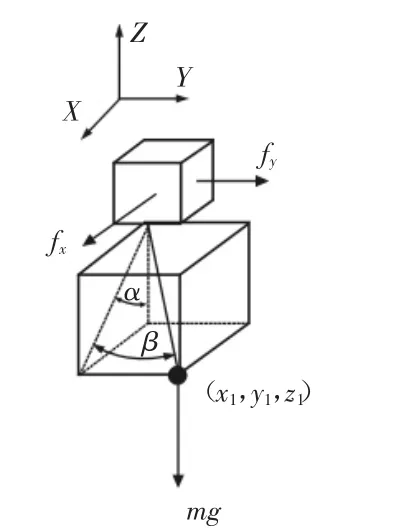
圖1 吊具工作三維示意圖Fig.1 Three Dimensional Sketch Map of Hanger

表1 CXTD16t-19.5m雙梁橋式起重機(jī)部分參數(shù)Tab1 Some Parameters of CXTD16t-19.5m Double Beam Bridge Crane

橋式起重機(jī)運(yùn)動(dòng)在某工作瞬態(tài)，假設(shè)其重物所處位置為（x1，y1，z1），小車(chē)所處位置為（x，y，0），則由圖 1 得：

橋式起重機(jī)系統(tǒng)動(dòng)能T為大小車(chē)、吊重三部分動(dòng)能之和，即：

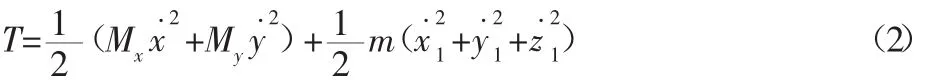
式中：x˙、y˙—大小車(chē)的位移速度；Mx、My—小車(chē)和整車(chē)質(zhì)量。

根據(jù)Lagrange方程與簡(jiǎn)化條件得其動(dòng)力學(xué)微分方程，如式

將方程組（3）解耦到x軸方向和y軸方向，分別得式（4）、式

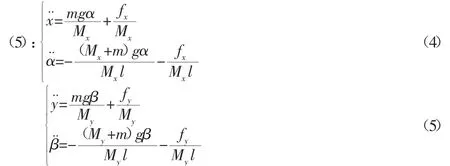
其中，各參數(shù)含義及初始值，如表2所示。

表2 參數(shù)含義及初始值表Tab2 Parameter Meaning and Initial Value

由式（4）、式（5），得到大小車(chē)狀態(tài)式（6）：

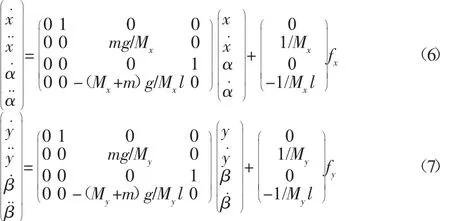
將表（2）參數(shù)代入式（6）、式（7）得大小車(chē)的狀態(tài)空間方程：

3 LQR控制原理

LQR（linear quadratic regulator）即線性二次型調(diào)節(jié)器，其基本原理是通過(guò)尋找最優(yōu)反饋矩陣K以達(dá)到最優(yōu)控制，使目標(biāo)函數(shù)J達(dá)到最小值，目標(biāo)函數(shù)為

式中：Q、R—狀態(tài)量和輸入變量的加權(quán)值[8]。

根據(jù)極大值原理，最優(yōu)控制為：U*=-KX

反饋矩陣K=R-1BTP，P為Riccati方程非負(fù)定對(duì)稱解，Riccati方程為：PA+ATP-PBR-1BTP+Q=0

用 MATLAB 中 LQR 函數(shù)求解 LQR（A，B，Q，R），可以求出最優(yōu)反饋系數(shù)矩陣K，加權(quán)矩陣Q，R矩陣。不同的K矩陣會(huì)有不同的Q、R和系統(tǒng)性能指標(biāo)。

4 模糊控制器設(shè)計(jì)

4.1 信息融合

由大小車(chē)動(dòng)力學(xué)方程設(shè)計(jì)LQR控制器的反饋矩陣有四個(gè)控制對(duì)象，以小車(chē)為例，即

反饋矩陣為：K=（KXKX˙KαKα˙）

模糊控制器的輸入為偏差量E和偏差變化率Ec，顯然四個(gè)輸入會(huì)存在模糊規(guī)則爆炸的問(wèn)題，因此必須對(duì)其降維處理，即信息融合技術(shù)。通過(guò)信息融合技術(shù)得：

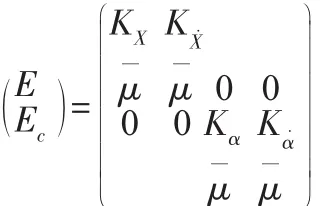
此時(shí)，模糊控制器的輸入由4維降到2維，滿足模糊控制器的輸入條件。

4.2 模糊控制策略

4.2.1 變量模糊化

經(jīng)過(guò)信息融合的反饋矩陣后以偏差E和偏差變化率EC輸入到模糊控制器中，即二維模糊控制器[9]。E、EC和輸出變量U均定義7個(gè)模糊子集，分別為負(fù)大、負(fù)中、負(fù)小、零、正小、正中、正大，分別用NB、NM、NS、Z0、PS、PM、PB表示，每個(gè)變量論域均定為［-3，3］，其隸屬度函數(shù)，如圖2～圖4所示。

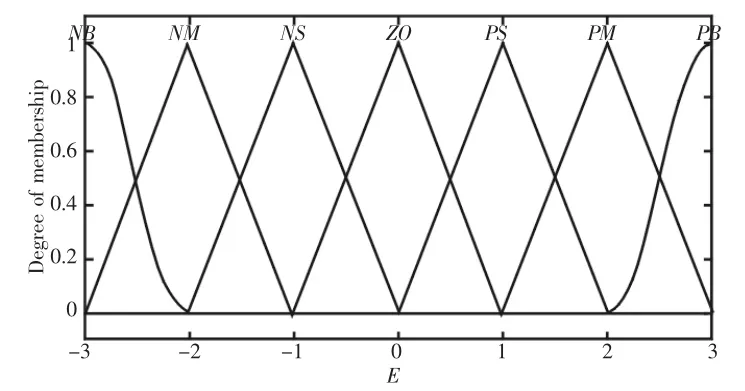
圖2 E隸屬度函數(shù)Fig.2 Membership Function Figure of E

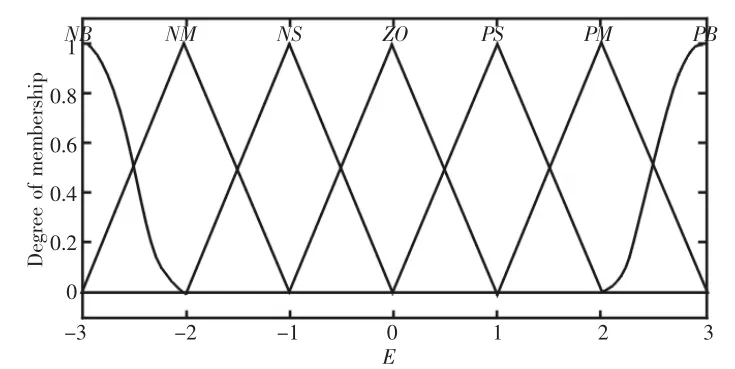
圖3 EC隸屬度函數(shù)Fig.3 Membership Function Figure of EC

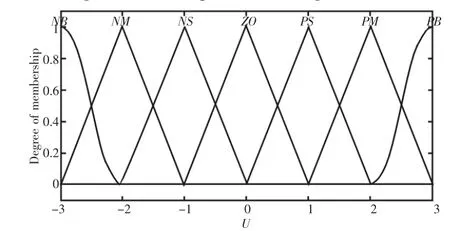
圖4 U隸屬度函數(shù)Fig.4 Membership Function of U

4.2.2 模糊推理規(guī)則

根據(jù)輸入變量和輸出變量論域的劃分，設(shè)計(jì)出Mamdani型的模糊推理規(guī)則，采用重心法解模糊，由于每個(gè)變量均有7個(gè)語(yǔ)言值，因此設(shè)計(jì)出49條規(guī)則，控制規(guī)則，如表3所示。

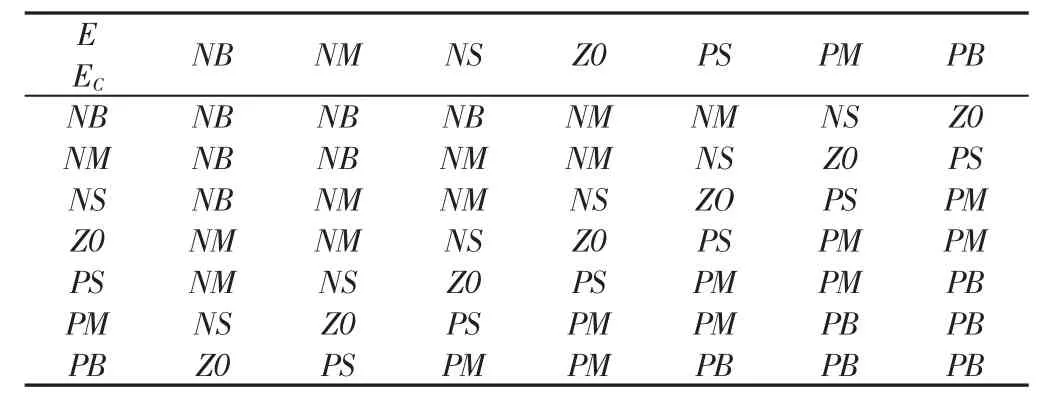
表3 模糊控制規(guī)則Tab.3 Fuzzy Control Rule

利用MATLAB的Fuzzy工具箱建立隸屬函數(shù)和推理規(guī)則。

4.2.3 量化因子

E、EC的量化因子KE、KEC將E、EC分別從基本論域轉(zhuǎn)換到各自的模糊集論域，控制量U的比例因子KU也需要將U從模糊集論域轉(zhuǎn)換到基本論域中[10]。量化因子除了對(duì)論域進(jìn)行變換外還使前后模塊匹配，對(duì)整個(gè)系統(tǒng)有調(diào)節(jié)作用，因此三者的大小通過(guò)仿真確定。

5 仿真

5.1 仿真模型

結(jié)合建立的動(dòng)力學(xué)方程在simulink中搭建大小車(chē)仿真模型及聯(lián)合仿真模型，如圖5、圖6所示。

圖5 小車(chē)控制仿真模型Fig.5 Control Simulation Model of the Crane Crolley

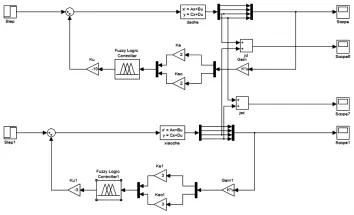
圖6 聯(lián)合控制仿真模型Fig.6 Joint Control Simulation Model

仿真過(guò)程中給定仿真初始值為（0，0，0.2，0），即給定的初始角度為0.3rad，輸入單位階躍信號(hào)，如圖5所示。大車(chē)仿真過(guò)程中給定仿真初始值為（0，0，0，0），即給定的初始角度為 0rad，輸入單位階躍信號(hào)；仿真過(guò)程中給定的仿真初始值為（0，0，0.5，0），即給定初始角度為0.5rad，輸入單位階躍信號(hào)，如圖6所示。

5.2 仿真參數(shù)的確定

由于系統(tǒng)的位移和角度對(duì)系統(tǒng)穩(wěn)定性影響最大，因此，取大車(chē)的加權(quán)矩陣 Q大=（300，1，200，1），R 大=1。利用 MATLAB 的LQR 函數(shù)求解得出反饋矩陣 K大=（17.32，21.68，-1.89，8.1108），計(jì)算出信息融合矩陣K*大：

小車(chē)的加權(quán)矩陣 Q=（450，10，300，10），R大=1。利用 MATLAB的 LQR 函數(shù)求解得出反饋矩陣 K小=（21.21，11.73，5.730，16.52），計(jì)算出信息融合矩陣：

KE、KEC、KU分別取 2、2、-10，仿真初始值取（0，0，0.2，0）。

5.3 仿真結(jié)果

吊重在未加入控制前的仿真結(jié)果，如圖7所示。由圖7可知未加入控制時(shí)吊重?cái)[動(dòng)初始角度為0.2rad，運(yùn)動(dòng)過(guò)程中擺角變化曲線和角速度變化曲線均做小幅度衰弱波動(dòng)。

分別對(duì)大小車(chē)進(jìn)行仿真，仿真結(jié)果，如圖8、圖9所示。由圖8 可知，給定初始值（0，0，0.2，0），在外界輸入的情況下，吊重各運(yùn)動(dòng)參數(shù)可以迅速達(dá)到平衡，擺角穩(wěn)定較快，歷時(shí)14s但存在超調(diào)，且在小車(chē)位移值達(dá)到0.9m時(shí)，小車(chē)速度、吊重?cái)[角、吊重角加速度達(dá)到穩(wěn)定。由圖9可知，在無(wú)初始值的情況下，當(dāng)大車(chē)輸入階躍信號(hào)時(shí)，大車(chē)速度、吊重?cái)[角、吊重角加速度在位移量為0.42m的時(shí)候達(dá)到穩(wěn)定狀態(tài)，但四個(gè)運(yùn)動(dòng)參數(shù)的調(diào)整時(shí)間長(zhǎng)，存在超調(diào)和抖振現(xiàn)象。由圖10可知，對(duì)大小車(chē)的聯(lián)合仿真時(shí)，給定初始狀態(tài)（0，0，0.5，0），經(jīng)過(guò) 30s的調(diào)整，基本可以達(dá)到穩(wěn)定狀態(tài)，15s吊重?cái)[角可以達(dá)到0.02rad范圍內(nèi)，但存在超調(diào)。

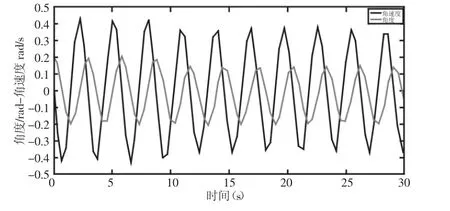
圖7 未加入控制時(shí)吊重參數(shù)變化曲線Fig.7 Parameter Changing Curve of Crane Load Without Adding Control

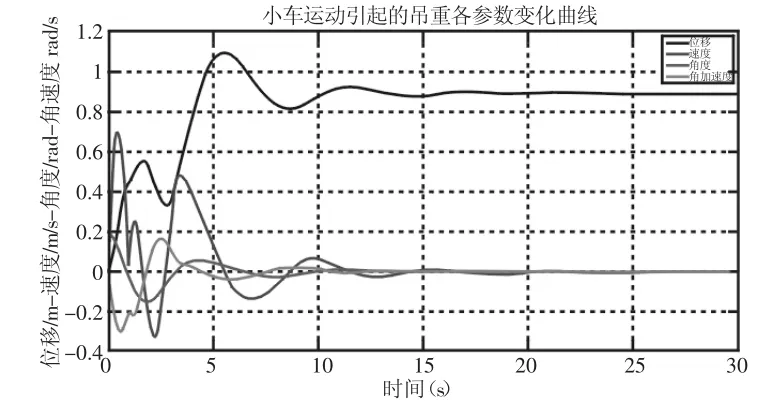
圖8 小車(chē)仿真結(jié)果Fig.8 Simulation Result of the Crane Rrolley Rontrol

圖9 大車(chē)控制仿真結(jié)果Fig.9 Simulation Result of the Crane Cart Control

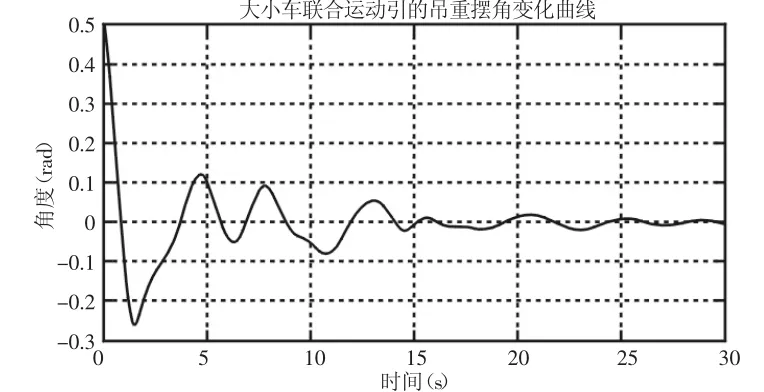
圖10 聯(lián)合仿真角度變化曲線Fig.10 The Curve Change of Angular of Joint Control Simulation

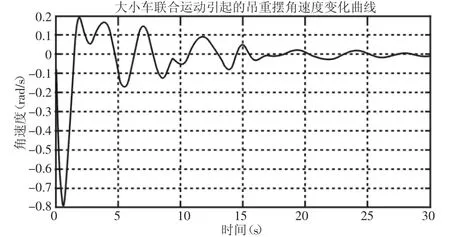
圖11 聯(lián)合仿真角速度變化曲線Fig.11 The Curve of Angular Velocity Change of Joint Control Simulation

6 結(jié)論

將吊重運(yùn)動(dòng)解耦到大小車(chē)的運(yùn)動(dòng)方向，分別利用大小車(chē)的運(yùn)動(dòng)控制吊重?cái)[動(dòng)以及利用二者聯(lián)合控制吊重?cái)[動(dòng)。對(duì)比加入控制前后的吊重?cái)[動(dòng)仿真結(jié)果表明，F(xiàn)uzzy-LQR控制方法可以完成對(duì)橋式起重機(jī)吊重的防擺定位，動(dòng)態(tài)響應(yīng)速度快，調(diào)整時(shí)間較短，且通過(guò)調(diào)整控制參數(shù)Q、R、KE、KEC、KU可以改變控制結(jié)果，調(diào)節(jié)超調(diào)量和動(dòng)態(tài)響應(yīng)速度。