正交各向異性錐殼外壓臨界失穩壓力研究

胡嘉琦，賀小華，周昌玉

1 引言

金屬鈦有著密度小、比強度高、耐腐蝕性強等特點，廣泛應用于壓力容器。鈦材在軋制過程中會出現織構現象，在軋制力作用下金屬晶體會集體擇優選擇朝向，導致鈦材各個方向的材料參數有顯著不同，所以鈦材是典型的正交各向異性材料[1-2]。目前，國內外標準[3-5]中將鈦材視為各向同性材料進行處理，該處理方式雖便于工程應用，但會給壓力容器設計帶來一定的不確定性。

外壓錐殼常用于航空航天、石油化工等領域，失穩是外壓錐殼失效的主要形式。文獻[6-7]對錐殼分別受軸壓、外壓和組合載荷作用下的屈曲失穩進行了實驗研究，測得的實驗值與理論公式計算值、標準解差異較大，由于有限元計算中考慮了實驗結構的初始缺陷，所以計算結果與實驗值較為接近。文獻[8]采用有限元分析方法對斜錐殼及其等效正錐殼進行外壓屈曲模擬計算，研究了兩種錐殼在屈曲失穩模態形狀的差異以及幾何參數對臨界失穩壓力的影響。

文獻[9]對正交各向異性薄壁圓筒臨界失穩進行有限元分析，比較了有限元解與解析解、標準解的不同，討論了材料不同卷板方式對臨界失穩壓力的影響，并對比分析了各向異性與各向同性外壓圓筒的差異。圓筒和錐殼結構都是壓力容器中常用結構，目前鮮有文獻對正交各向異性錐殼外壓失穩進行系統研究，關于正交各向異性和各向同性錐殼的差異性也未進行討論分析。文獻[10]依據Donnell理論，結合相關力學關系列出正交各向異性錐殼受外壓時的平衡方程，并依據Galerkin&Ritz理論求解出正交各向異性變厚度錐殼臨界失穩靜壓力和動壓力計算公式。實際工程中，錐殼在制造過程中會造成結構缺陷，理論公式能否適用于實際工程中尚需進一步討論。采用有限元分析法對正交各向異性錐殼進行外壓失穩模擬計算，系統研究幾何參數對臨界失穩壓力Pcr的影響，對比分析正交各向異性與各向同性錐殼的差異，討論現行規范計算正交各向異性錐殼臨界失穩壓力方法的可行性。結果對進一步實現正交各向異性錐殼結構優化，有效提高承載能力具有重要意義。

2 外壓錐殼有限元模擬

2.1 TA2正交各向異性材料參數

錐殼材料為工業純鈦TA2。通過實驗測定TA2的材料參數[1]，實驗數據，如表1所示。其中，x方向為板材軋制方向，y方向板材寬度方向，z為板材厚度方向。

表1 TA2材料參數Tab.1 Material Parameters of TA2

2.2 有限元計算模型

為了研究結構幾何參數對正交各向異性錐殼臨界失穩壓力的影響，保持錐殼大端外直徑DL不變，通過改變錐殼半頂角α以及徑厚比來建立模型進行模擬分析。計算方案中DL=3000mm，徑厚比 DL/T 值為 80、100、150、250，錐形比 λ（λ=1-Ds/DL）值為 0.35、0.5、0.65，半頂角 α 取值范圍為（5～60）°，中間間隔 5°。采用shell181單元對模型進行網格劃分，并進行網格無關性驗證，shell181單元的有效可靠性在文獻[2]中已有詳細說明。

2.3 有限元模擬邊界條件

參照文獻[8，10]，錐殼大小端邊界條件均采用簡支約束，大小兩端均約束環向位移，小端同時約束軸向位移，錐殼外表面施加壓力。

2.4 有限元結構失穩分析方法

有限元失穩分析中，常使用特征值分析法和非線性分析法，但兩種方法計算時常會得出相差較大的結果。為了驗證兩種方法的可靠性，選取文獻[6-7]中錐殼外壓實驗模型，分別進行特征值分析和非線性分析，其中在非線性分析過程中采用“一致缺陷模態法”，施加實驗模型的初始缺陷。分析所得的臨界失穩壓力，如表2所示。通過將兩種方法的有限元計算結果與實驗值對比可知，特征值分析結果與實驗值相差較大，而非線性分析結果與實驗值較為接近。由于考慮了模型的初始幾何缺陷以及幾何大變形等因素，故采用有限元非線性分析求解的臨界失穩壓力較為準確。

表2 不同分析方法得到的臨界失穩壓力Tab.2 The Critical Buckling Pressure Calculated by Different Methods

3 外壓錐殼臨界失穩壓力研究

錐殼在設備中常起連接作用，主要的連接形式有圓筒—錐殼—圓筒。當上下所連接圓筒直徑與厚度都確定時，在滿足工程使用條件下，只能通過變化錐殼半頂角來改變殼體結構。

選取錐形比λ=0.5的錐殼為研究對象，利用非線性分析法研究不同幾何參數下正交各向異性錐殼臨界失穩壓力。模擬過程中將標準[3]所規定的最大允許偏差作為模型的初始幾何缺陷施加。模擬所得臨界失穩壓力Pcr，如圖1（a）所示。

圖1 正交各向異性錐殼臨界失穩壓力Fig.1 The Critical Buckling Pressure of Orthotropic Conical Shell

從圖中可知，隨著錐殼半頂角的增大，Pcr先增大后逐漸減小。分析認為，在其他結構參數不變時，錐殼軸向長度的縮短對錐殼臨界失穩壓力Pcr有著兩種不同的作用。一方面，隨著錐殼軸向長度的縮短，錐殼受大小端支撐線的邊緣效應作用逐漸加強，有助提高外壓穩定性；另一方面，隨著錐殼半頂角α的增大，對錐殼外壓穩定性有抑制作用，與文獻[8]結論一致。

綜合考慮錐殼大小端增強影響和錐殼半頂角大小等因素，可有效提高錐殼的抗失穩能力。從圖中可得，不同徑厚比的錐殼結構，在半頂角從（5～60）°的變化過程中，Pcr最大值與最小值的比值可達到（1.9～3.6）。錐殼在半頂角30°附近的抗失穩能力最強。對于單一使用的錐殼，還可通過改變徑厚比有效提高錐殼抗失穩能力。

為驗證上述規律的一般性，選取徑厚比DL/T=100，錐形比λ為0.35、0.6的錐殼進行模擬計算，模擬結果，如圖1（b）所示。從圖中可得，不同錐形比的錐殼，其中，Pcr隨半頂角的變化規律基本相同。由此說明，一定錐形比及徑厚比下，在半頂角30°附近，錐殼抗外壓失穩能力最強。

4 外壓錐殼臨界失穩壓力的比較

4.1 正交各向異性錐殼臨界失穩壓力與理論公式計算結果比較

文獻[10]推導出簡支條件下正交各向異性錐殼外壓臨界失穩靜壓力公式：

式中：Eθ、Et—錐殼環向和母線方向上的彈性模量；vtθ、vθt—泊松比；r2—閉合錐殼母線長度；γ—錐殼半頂角；b1、b2、b3、b5、b6—相關系數，詳見文獻。

利用式（1）分別計算不同幾何參數的錐殼臨界失穩壓力Pcr，選取錐形比λ=0.5的錐殼為例，理論公式與有限元計算結果，如圖2所示。從圖中可知，徑厚比較小時，相同參數下，Pcr解析解遠大于有限元解。解析解的變化規律與有限元解較為相似，隨著錐殼半頂角的增大，Pcr先增大后逐漸減小。解析解與有限元解達到最大值時半頂角范圍存在差異，解析解在半頂角40°附近時最大，而有限元解則在半頂角30°附近時達到最大值。

為了進一步分析解析解與有限元解的差異性，以及討論理論公式在工程設計中的適用性，正交各向異性臨界失穩壓力Pcr有限元解與解析解比值，如圖2所示。P1為有限元解，P2為解析解。從圖中可知，隨著錐殼半頂角的增大，P1/P2值逐漸減小而后趨于一定值。不同錐形比下，P1/P2變化規律基本一致。由于理論公式解適用于薄殼且未考慮缺陷，徑厚比較大時，有限元解與解析解較為一致，徑厚比較小時，有限元解與解析解差異較大。

由圖 2可知，不同錐形比下，在半頂角（20～45）°范圍內，當徑厚比DL/T≥150時，P1/P2值范圍為（0.8～1.2），Pcr解析解與有限元解具有較好的一致性，可適用于工程設計中。

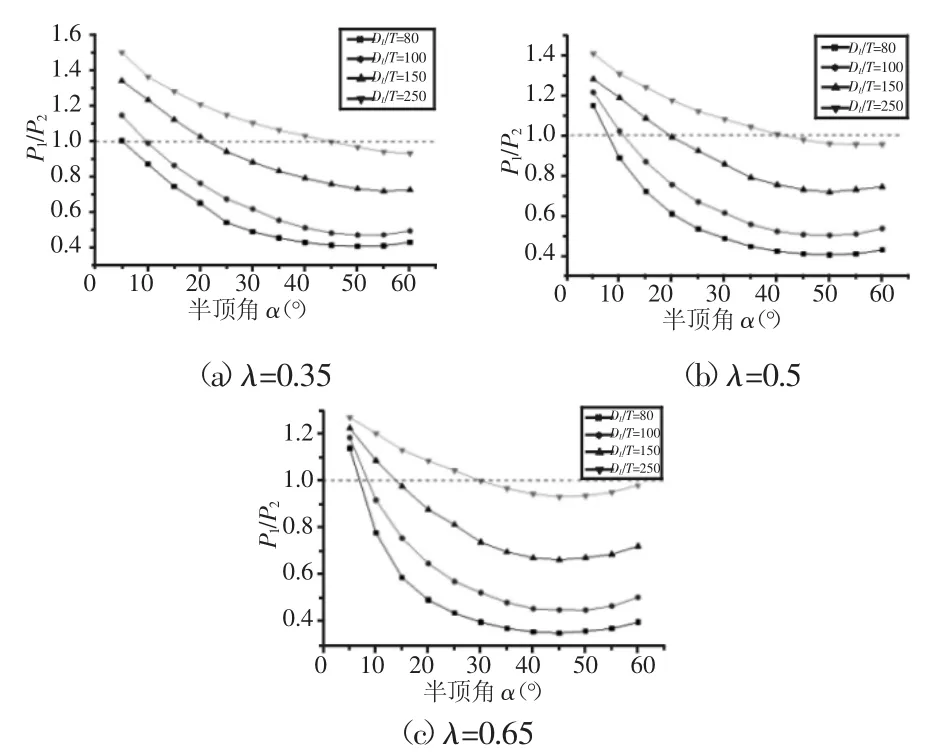
圖2 正交各向異性錐殼臨界失穩壓力有限元解與解析解比Fig.2 The Ratio of Critical Buckling Pressure Between Finite Element Solution and Analytical Solution

4.2 正交各向異性與各向同性錐殼臨界失穩壓力的比較

標準[3-5]中將鈦材視為各向同性材料，其應力—應變曲線是按鈦材軋制方向拉伸繪制的，泊松比取0.32。為比較正交各向異性與各向同性錐殼之間的差異，各向同性錐殼臨界失穩壓力模擬計算中，材料參數取板材軋制方向數值。選取錐形比λ=0.5的錐殼為例，各向同性與正交各向異性錐殼臨界失穩壓力Pcr，如圖3所示。從圖3中可知，正交各向異性性錐殼臨界失穩壓力變化規律與各向同性錐殼基本相同，相同參數下，正交各向異性錐殼臨界失穩壓力值均大于各向同性錐殼。

圖3 正交各向異性與各向同性錐殼失穩壓力Fig.3 The Critical Buckling Pressure of Orthotropic Conical Shell and Isotropic One

為了進一步分析正交各向異性與各向同性錐殼的差異性，正交各向異性與各向同性錐殼臨界失穩壓力的比值，如圖4所示。圖中：P3—各向同性錐殼臨界失穩壓力。從圖中可知，隨著錐殼半頂角、徑厚比和錐形比的增大，P1/P3值逐漸減小，但減小的幅度都不大，相同參數下，正交各向異性錐殼臨界失穩壓力值普遍高于各向同性錐殼（15～23）%。由于正交各向異性材料的力學參數和本構關系與各向同性材料有一定的差異，使得兩者之間的抗彎模量和抗扭剛度有所不同，導致兩者的抗失穩能力也不同，正交各向異性錐殼的抗失穩能力要強于各向同性錐殼。

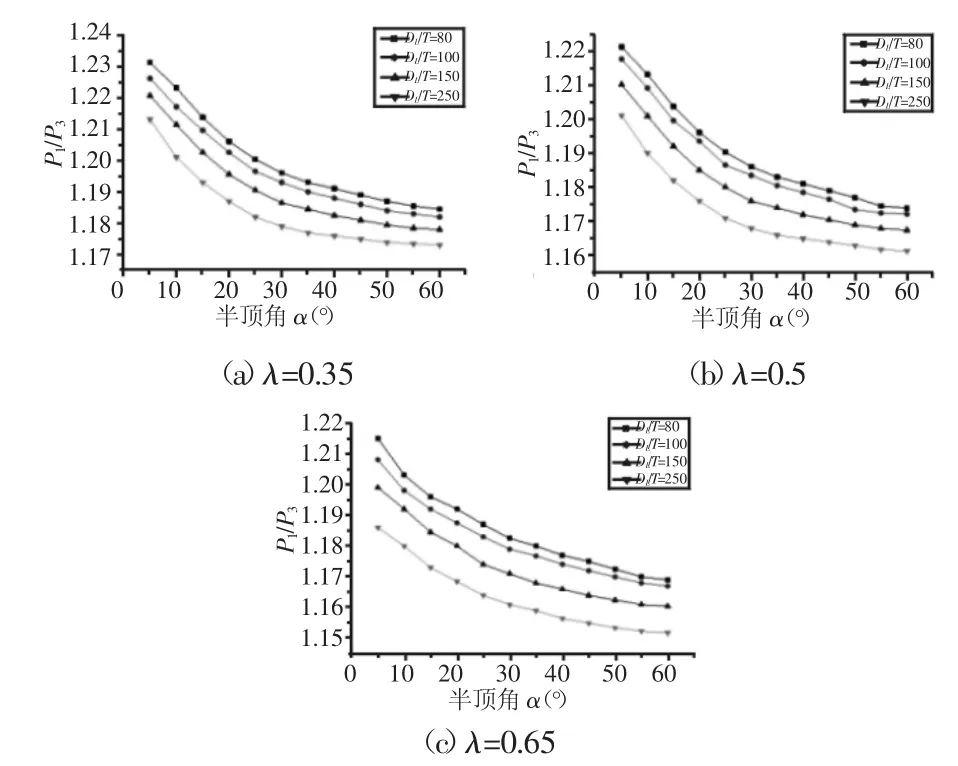
圖4 正交各向異性與各向同性錐殼臨界失穩壓力比Fig.4 The Ratio of Critical Buckling Pressure Between the Orthotropic Conical Shell and Isotropic One

4.3 正交各向異性錐殼與等效各向同性圓筒臨界失穩壓力的比較

錐殼外壓失穩問題相對比較復雜，相關實驗研究表明，錐殼失穩過程與等效圓筒失穩過程相似，所以標準中將錐殼等效成圓筒進行設計。標準[3，5]中采用等效方法處理錐殼穩定性問題，其等效圓筒直徑d=（DL+Ds）/（2cosα），等效圓筒長度為錐殼母線長度L，等效圓筒厚度為錐殼厚度T。由于現行設計標準中將鈦材視為各向同性材料，故正交各向異性錐殼被等效成各向同性圓筒進行設計，為了比較分析兩者之間的差異性，將不同幾何參數的正交各向異性錐殼等效成各向同性圓筒，模擬計算其臨界失穩壓力，圓筒的邊界約束條件與錐殼相同，計算過程中模型施加等量的初始幾何缺陷。選取錐形比λ=0.5的錐殼為例，等效各向同性圓筒與錐殼臨界失穩壓力Pcr，如圖5所示。從圖中可知，正交各向異性錐殼臨界失穩壓力變化規律與等效各向同性圓筒基本相同，相同參數下，正交各向異性錐殼臨界失穩壓力值均大于等效各向同性圓筒。

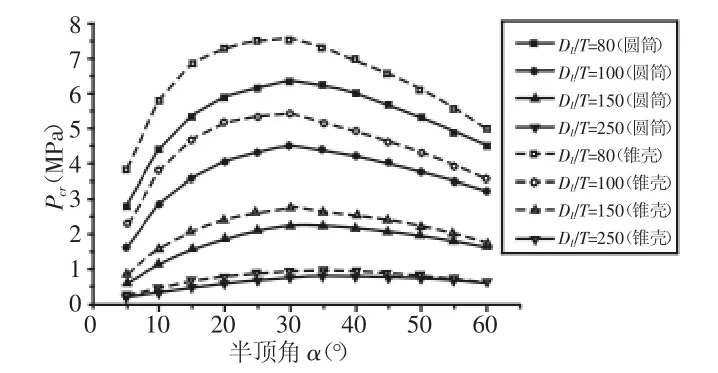
圖5 正交各向異性錐殼與等效各向同性圓筒臨界失穩壓力Fig.5 The Critical Buckling Pressure of Orthotropic Conical Shell and Equivalent Isotropic Cylinder

為了進一步分析正交各向異性錐殼與等效各向同性圓筒的差異性，正交各向異性錐殼與等效各向同性圓筒的臨界失穩壓力比，如圖6所示。圖中：P4為等效各向同性圓筒臨界失穩壓力。從圖中可知，隨著半頂角的增大，P1/P4值不斷減小，正交各向異性錐殼臨界失穩壓力值與等效各向同性圓筒差異逐漸減小。隨著錐形比的增大，正交各向異性錐殼臨界失穩壓力值與等效各向同性圓筒差異逐漸增大。

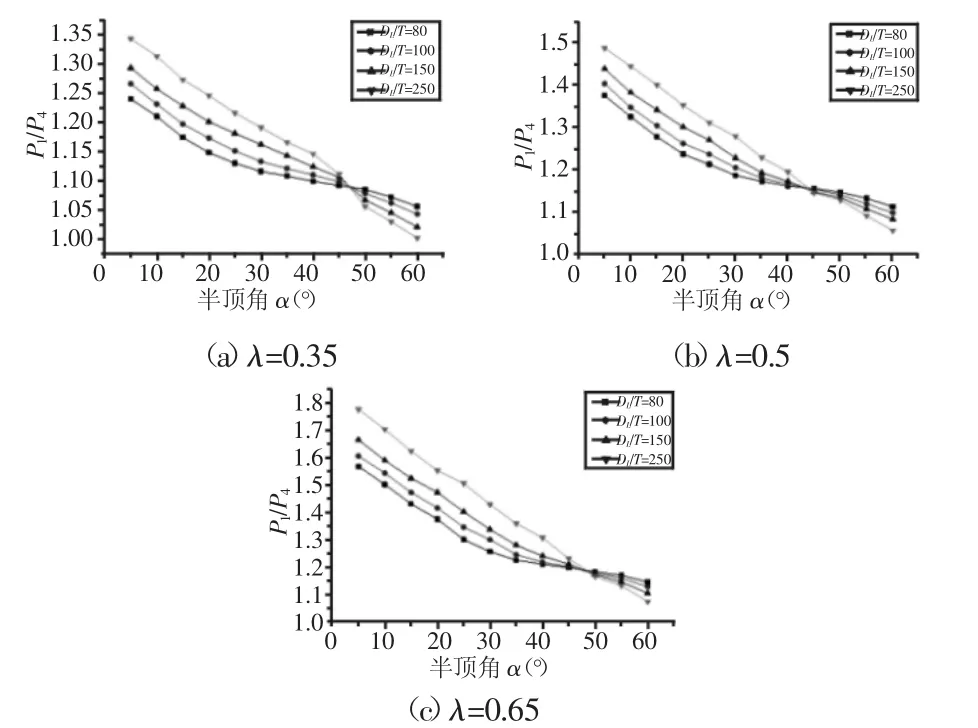
圖6 正交各向異性錐殼與等效各向同性圓筒臨界失穩壓力比Fig.6 The Ratio of Critical Buckling Pressure Between Orthotropic Conical Shell and Equivalent Isotropic Cylinder

工程設計中，正交各向異性錐殼等效成各向同性圓筒具有保守性。當錐殼半頂角較小時，正交各向異性錐殼等效成各向同性圓筒具有較高的安全富裕量；當錐殼半頂角較大時，正交各向異性錐殼等效成各向同性圓筒安全富裕量適可。

5 結論

利用有限元非線性分析法，對不同幾何參數的正交各向異性錐殼臨界失穩壓力進行系統研究，模擬計算結果與理論公式、各向同性錐殼以及等效圓筒進行比較，得到以下結論：

（1）在其他幾何參數不變的情況下，隨著錐殼半頂角的增大，正交各向異性錐殼臨界失穩壓力先增大后逐漸減小，半頂角在30°附近，錐殼外壓抗失穩能力最強。

（2）錐殼徑厚比較大時，解析解與有限元解有較好的一致性，錐殼在半頂角（20～45）°范圍內，當徑厚比 DL/T≥150 時，解析解可適用于工程設計中。

（3）正交各向異性錐殼臨界失穩壓力值普遍高于各向同性錐殼（15～23）%。

（4）正交各向異性錐殼等效成各向同性圓筒具有保守性。當錐殼半頂角較小時，正交各向異性錐殼等效成各向同性圓筒具有較高的安全裕量；當錐殼半頂角較大時，正交各向異性錐殼等效成各向同性圓筒安全裕量適可。