裝配偏差分析的區間算法

衡德正，羊 軍，金愛君 ，金 隼

1 引言

裝配偏差分析作為連接產品設計與制造的關鍵環節，通過將設計目標與制造能力集成在一個模型，定量化的評估零件制造偏差對產品功能的影響，在滿足產品功能要求的前提下，力爭使產品的制造成本最低。

裝配偏差分析一般包括極值法和統計法。極值法基于零件滿足100%互換，即在組成環中增環為極大（小）值、減環為極小（大）值時，封閉環取得極大（小）值。但實際尺寸鏈中，各個組成環一般為不確定量，按照極值法計算必然帶來分析結果趨于保守，帶來制造難度提高，制造成本增加。統計偏差分析考慮了零件尺寸偏差的分布特性，更符合實際狀況，受到廣泛應用。但統計偏差分析一般基于概率論，將各個偏差變量視為隨機變量，需要大量的不確定信息來判斷尺寸的統計分布形式[1]。現代機械產品，組成零件多，工藝流程復雜，各種偏差經過復雜的傳播、耦合，形成最終裝配偏差，一般很難知道偏差變量的具體分布形式。此外，概率模型并不是描述偏差不確定性的唯一模型，而且研究表明，不確定性未必就是隨機性，也可能是模糊性或未知而有界性。同時，概率模型對于參數的擾動特別敏感，以至于很小的誤差也會帶來計算結果的較大誤差，在缺乏足夠樣本信息時，一旦對這些概率分布的假定和工程參數的真正分布不符，則統計偏差分析結果的合理性與可靠性就失去意義。對此，提出裝配偏差的區間算法。用區間的大小度量不確定量的變化程度。區間法只需要知道尺寸的上下限而不需要知道具體的分布形式，這就大大降低了對裝配偏差分析的數據要求[2-3]，更適用于裝配偏差分析。文獻[4]用區間表示輸入參數，并結合cost-tolerance模型進行公差優化；文獻[5]提出用幾何實體小自由度描述尺寸和形狀公差，特征參數的不確定用區間表示，從而進行裝配偏差分析；文獻[6]為保證機器人末端執行器的精度，用區間表示機器人制造和裝配過程的不確定因素，并進行關節處的公差優化；文獻[7]提出了一種利用區間數求解平面尺寸鏈的新方法；文獻[8]提出了一種考慮公差設計的區間優化算法，在保證目標性能的同時最大化設計變量的公差帶，提高制造工藝性和降低制造成本。

上述基于區間法的參數計算與優化過程中，沒有考慮區間擴張對最終參數的影響，對此提出了基于截斷區間法的裝配偏差分析模型，以有效的減小區間擴張對偏差分析結果的影響，提高計算結果的可靠性與實用性。

2 區間法的基本原理

在區間分析中，結構的不確定參數以一個區間的形式表示，同時結構響應也以區間形式給出。在裝配偏差分析中，我們很容易知道尺寸參數的上下界，不必再對這些參數的分布情況做出假設，下面給出區間法的基本原理。

定義1.1設R為實數域，對于給定的兩個實數x，x∈R，且x≤x ，則 XI=［x，x］，稱為閉區間，簡稱區間。

定義1.2對于任意兩個區間XI=［x，x］，YI=［y，y］，區間四則運算為：

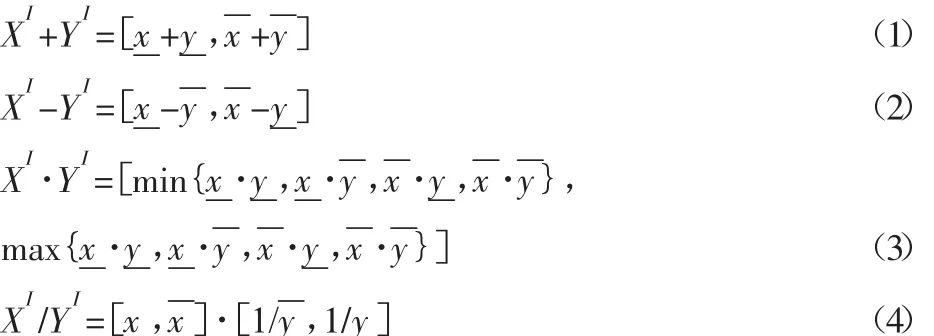
3 區間上下界的確定

對于一個由不同零部件裝配而成的機械產品而言，裝配尺寸鏈中各個組成環的變化區間均為已知參數，要想知道封閉環的變化區間，最簡單的方法就是根據公差設計函數，按照上面給出的區間運算的法則進行求解。一般而言，當組成環的數目和封閉環的變化區間都較小時，這種區間運算能夠取得比較精確的結果，但當組成環的數目和封閉環的區間增大時，直接進行區間運算得到的結果往往會有較大誤差，不符合實際工程要求。造成這類現象的原因，主要是實數的運算法則僅有一部分適用在區間分析，如交換律。而對于分配率僅表現為弱的包含關系：X（IYI±ZI）?XI×YI±XI×ZI，由上面的運算法則可知，當輸入變量的數目以及運算次數增加時，區間運算會帶來較大的區間擴張，甚至失去應用價值，為限制這種擴張，引入改進區間截斷算法來確定封閉環尺寸的上下限[9]。假設兩個組成環尺寸變量aI=［a，a］，bI=［b，b］，封閉環尺寸變量 cI=［c，c］，并設 a0=m（aI），b0=m（bI），c0=m（cI），當 c0很小時，截斷法失效，否則我們可以計算出c0的相對偏差：

總的偏差為：Δ=Δ1+Δ2，假設最大偏差Δ為2t，并可通過以下改進的截斷區間［d，d］來求取c的取值上下限：

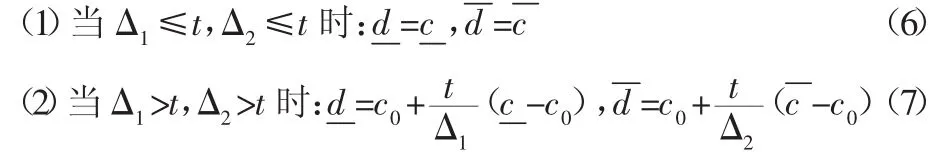
4 裝配偏差敏感性分析

裝配偏差的敏感性分析指計算一個或多個組成環的變化所導致的封閉環的變化幅度，從而更好的了解各個組成環對實現預期封閉環目標的影響程度。

目前，一般采用直接求導法、差分法或者攝動法求解裝配偏差的敏感性。然而在尺寸鏈的組成環與封閉環是隱式函數時，直接求導法很難應用。當組成環與封閉環是強非線性問題時，差分法或攝動法將嚴重影響敏感性分析的精度。將以區間法為基礎，進行裝配偏差的敏感性分析。假設一個結構具有n個組成環尺寸參數，這些組成環尺寸參數以名義值為中心構成一個區間向量，m 個封閉環尺寸構成另一個區間向量，那么這個裝配過程構成一個組成環尺寸至封閉環尺寸的映射：X→Y。根據區間數學的相關性質，在封閉環尺寸中，分別對輸入參數X（Iii=1，2，…，n）作區間擴張，可以得到：

式中：XIi—區間變量，其他參數均為實參數。

基于以上區間擴張等式，將區間向量XIi=［Xi0，Xi0］，其中 Xj0（j≠i）為組成環名義值，帶入式（3）～式（1），可得：

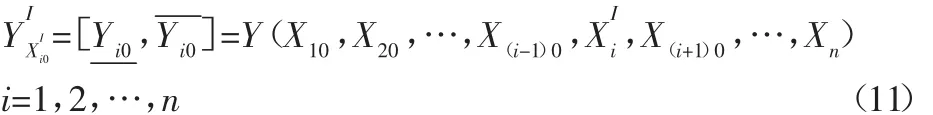
式中：XIi0—區間變量，其他參數均為組成環名義值。并定義敏感

通過比較S的大小，即可找出封閉環尺寸對哪個組成環參數更為敏感。

區間法可以在組成環任意給定的局部或全局范圍內，給出封閉環的變化量。雖然區間法給出的界限可能會比較粗糙，但是敏感度分析要求的是一種相對信息，界限的粗糙對相對信息間的比較不會帶來影響。

5 案例分析

為了驗證基于區間分析的裝配偏差分析方法的有效性，以如圖的單向離合器為例進行介紹[10]。該單向離合器包括一個內星輪、一個外圈和四個滾柱。這是一個常用的僅能在一個方向進行傳動的設備，當離合器的外圈順時針旋轉時，內星輪和外環中間的滾柱，將會帶動二者一起轉動，反向時，滾珠僅僅滑動，因而內星輪沒有轉動，如圖所示的兩個接觸點之間的壓力角Φ1對于離合器的正確操作至關重要，如果Φ1過大，將會使離合器鎖住，反之則無法鎖住。這里內星輪尺寸為a，滾柱半徑為c，外圈半徑為e，尺寸 b 和壓力角 Φ1則由 a、c、e決定，并要求公差 TΦ1=±0.6°，Tb=±0.5。各個組成環及封閉環的尺寸信息，如表1所示。

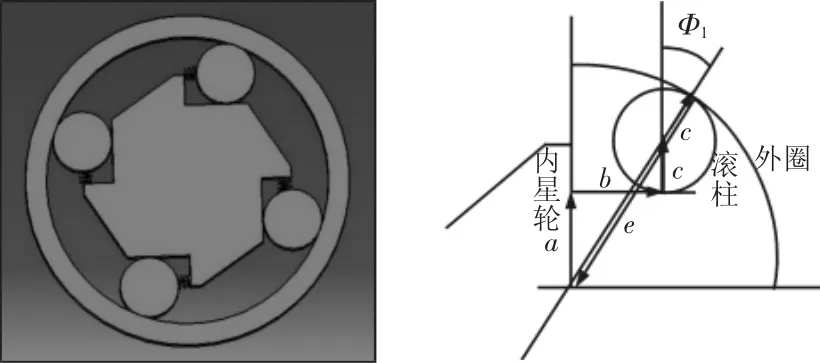
圖1 單向離合器及矢量環Fig.1 One-Way Clutch and Vector Loop

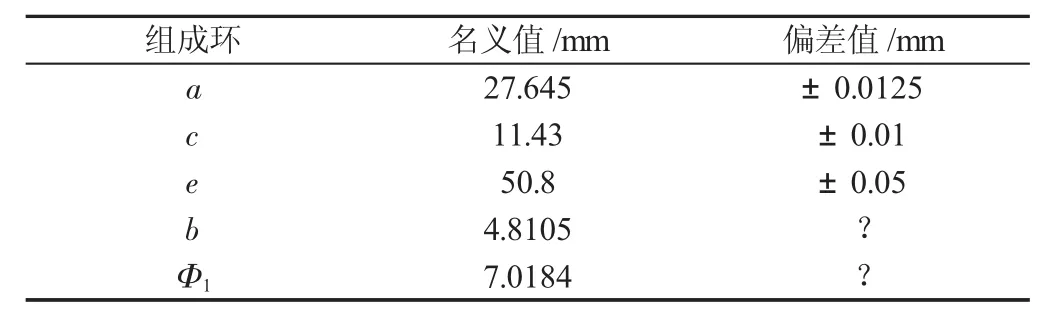
表1 尺寸信息Tab.1 Dimension Information

5.1 裝配偏差分析

為了分析單向離合器的裝配偏差，按照如圖所示的矢量環，建立矢量環方程：

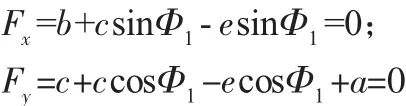
從而可得：Φ1=a cos（a+c）（e-c））；b=sqrt（（e-c）^2-（a+c）^2）

將組成環尺寸信息表示為區間形式：

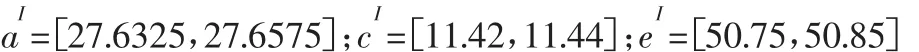
區間運算過程采用基于Matlab的Intlab工具箱，分別將上述區間變量帶入可以得到：

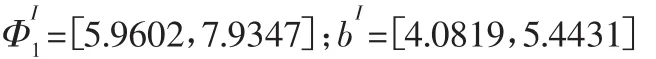
在設計過程出于保守考慮，我們希望總的偏差Δ大于真實值，并設相應的最大偏差2t在公差要求極限時取得，帶入式（5）求得：tΦ=0.0855，tb=0.1039

對于壓力角 Φ1，由式（5）可得：Δ1=0.1515＞tΦ，Δ2=0.1315＞tΦ

由截斷算法式（7）可得：ΦI

1=［6.928，7.0966］

同理可得：bI=［4.3108，5.3103］

將極值法、方根法應用于該案例，求得裝配偏差區間，如表2所示。通過表2可以看出，區間法和方根法求得的壓力角Φ1和b偏差均小于極值法，而且對于壓力角Φ1，區間法求取的裝配偏差小于方根法，對于b，區間法求取的裝配偏差和方根法基本相等。考慮到區間法求取的裝配偏差基于100%置信區間，而且不考慮參數的具體分布形式，而方根法給出±3σ的范圍，基于99.73%的置信區間，從而我們可以認為區間法求取的裝配偏差具有更高的可信性與準確度。

表2 不同方法偏差分析對比Tab.2 Comparing the Different Methods for Deviation Analysis

5.2 參數敏感性分析

根據式（12），分別求解壓力角Φ1和b對幾何參數a，c，e的敏感性系數，如圖2、圖3所示。

圖2 壓力角參數敏感性Fig.2 Sensitivity to Parameter of Pressure Angle

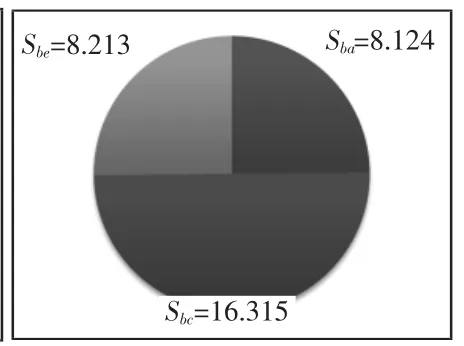
圖3 尺寸b參數敏感性Fig.3 Sensitivity to Parameter of Dimension b

從圖2、圖3可以看出，壓力角Φ1和b均對幾何尺寸c最為敏感，因而為了更好的控制壓力角和尺寸b，對內星輪幾何尺寸c的控制極為重要。

6 結論

針對極值法計算趨于保守和統計法依賴尺寸分布形式的缺點，提出了基于區間法的裝配偏差分析方法，將零件偏差與裝配偏差均表示為區間形式，并求解零件偏差的敏感性。通過單向離合器的實例分析，我們可知：（1）基于區間法的裝配偏差分析可以有效避免對尺寸信息分布形式以及概率密度函數的依賴，大大降低了裝配偏差分析對于數據的要求。（2）在區間分析中引入截斷算法，可以有效的避免區間擴張，克服區間算法的保守性，增強偏差分析結果的可靠性與實用價值。（3）傳統的敏感性分析以偏導數為基礎，給出的結果是某個小鄰域內的敏感性信息。基于區間法的敏感性分析尺寸范圍可以任意給定，滿足裝配偏差敏感性分析的全局性要求。