動態軋制力下冷連軋機超亞諧共振特性分析

彭榮榮，鞏長芬，王國威，秦梅寶

1 引言

冷連軋機的振動問題一直頗受國內外學者的關注，加之隨著當代生產技術水平的不斷提高，鋼鐵行業對軋制速度、產品質量和精度等的要求也隨之提高，而冷連軋機輥系的振動會造成帶材質量、精度等下降，嚴重時可導致帶材斷裂、設備損壞、次品積累，給企業造成困擾和經濟損失[1-3]。

海內外學者對冷連軋機的振動形式和機理從各種角度、不同影響因素進行了分析探究，建立了多種振動模型，對抑制軋機振動取得了很好成果。文獻[4-5]建立了受前后張力和軋制速度影響的軋機垂直振動模型，分析了帶鋼動態運動的穩定性，提出了相應的抑制措施；文獻[6]探討了摩擦因數對軋機垂直振動的影響，得出了軋制乳化液的潤滑性能與摩擦因數之間的非線性關系；文獻[7-9]對四輥板帶冷軋機在輥縫變形較大情況下的振型做了詳細分析，發現在某些特定頻率下軋機工作輥和支承輥在垂直方向上的振動幅度較大，且在這個過程中摩擦力的影響極大；近年來，研究人員對影響軋制力的種種因素進行了深入分析，通過考慮軋輥及軋件的彈塑性變形、帶鋼厚度、張力、輥縫接觸弧長、軋制速度、潤滑等不同因素影響下的軋制力模型，在此基礎上，文獻[10-13]提出了動態軋制力這一概念，其更加符合軋機實際振動過程中的動態變化。在動態軋制力的基礎之上，考慮了冷連軋機的機械結構、輥系間的阻尼及非線性剛度、周期性外激力等因素，建立了基于動態軋制力的冷鏈軋機振動模型，得到了相應的動力學方程，研究了在不同參數變化下的冷連軋機3次超諧共振和1/3亞諧共振幅頻特性，仿真分析給出了這兩種具有不同振動特性下軋機穩定運行和發生失穩時的參數區域，可以避免參數的選取不合理而導致的軋機劇烈振動。

2 軋機振動系統動力學建模

四輥冷連軋機的簡化模型，如圖1所示。將上支承輥等效稱成一個集中質量塊[13]，且考慮軋機到上、下輥系以及沿軋件運動方向的上、下兩部分振動具有高度對稱性[10]，建立了基于動態軋制力下的冷連軋機非線性振動動力學模型，如圖2所示。

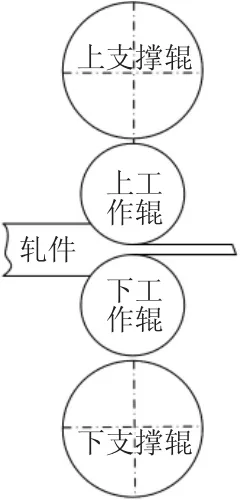
圖1 四輥冷連軋機簡化模型Fig.1 The Simplified Model of Four-High Cold Rolling Mill

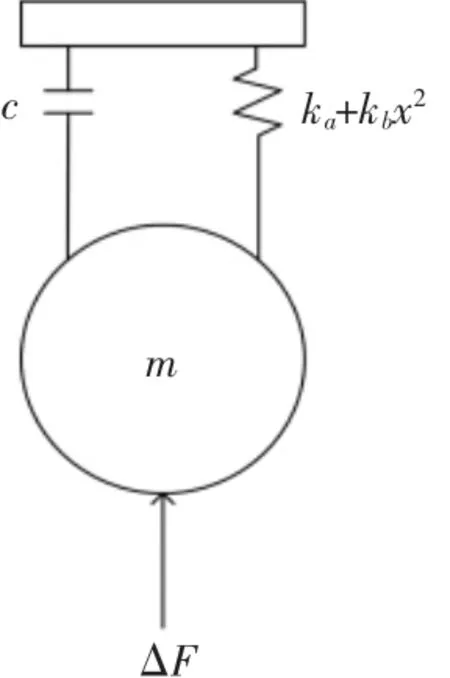
圖2 冷連軋機非線性振動動力學模型 Fig.2 The Nonlinear Vibration Dynamic Model of Cold Rolling Mill

圖中：m—冷連軋機工作輥的等效質量；c—其結構阻尼，用Duffing振子ka+kbx2表示支承輥與工作輥之間的非線性剛度[14-15]，ka，kb—靜態及動態剛度；ΔF—軋制力的動態變化部分，是關于振動位移 x的非線性函數[10]，ΔF=b1x+b2x3。b1，b2—待定常數。由圖2的力學模型可得冷連軋機動力學振動方程為：

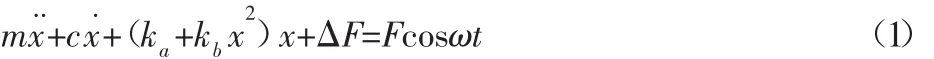
式中：F cosωt—冷連軋機受到的周期性外激力，且令式（1）中：

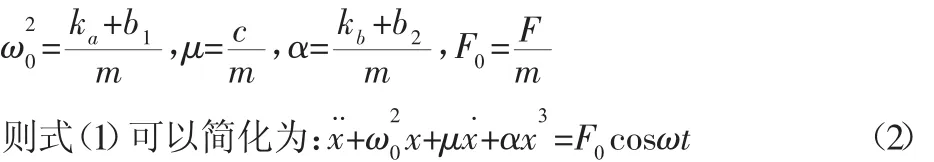
式（2）為考慮軋機結構，輥系間的非線性剛度，動態軋制力以及周期性外激力影響的冷連軋機動力學方程，是研究分析軋機振動特性的基礎。

3 軋機振動系統響應求解

式（2）中的冷連軋機動力學方程屬于弱非線性系統，對其中非線性項同時冠以小參數ε，則式（2）可進一步寫為：

對式（3）運用多尺度法求解，此時引入不同尺度的時間變量，即：

對時間t的微分可利用復合函數微分公式按ε的冪次展開：

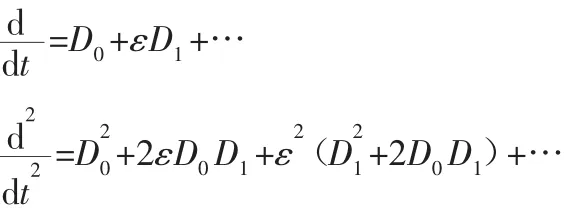
式中：Dn—偏微分算子符號，此時，關于式（3）的解可以表示為：

將式（5）代入式（3），且比較方程兩邊小參數ε的同次冪系數，整理可得：

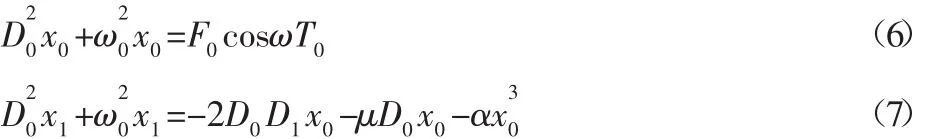
設零次近似方程（6）的解為：

式中：A—復數形式的振動振幅；Λ—振動振幅的實數形式，且有：

將零次近似解代入式（7），整理后可得：

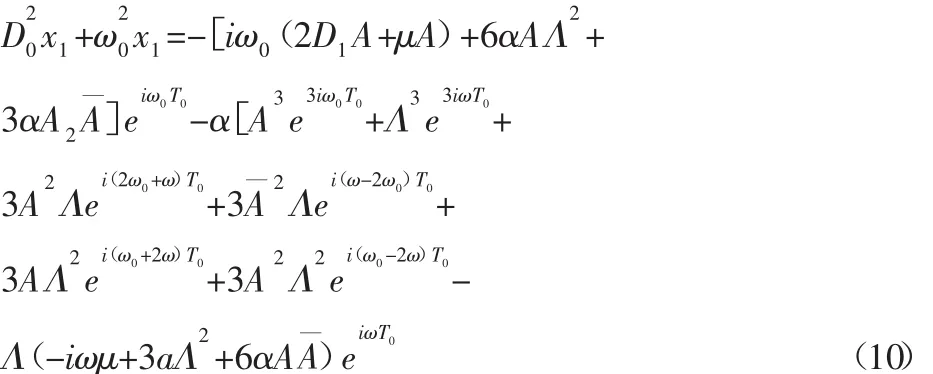
從上式各項中可以看到，含有的eiω0T0項可引起久期項，產生主共振，而e3iω0T0和ei（ω-2ω0）T0項在滿足3ω=ω0或ω=3ω0時也能產生久期項，從而產生超諧和亞諧共振。下面主要討論在動態軋制力下冷連軋機振動系統發生3次超諧共振和1/3次亞諧共振的情形。

3.1 超諧共振幅頻特性方程

設ω0與3ω的差別為ε的同階小量，即3ω=ω0+εσ，σ為調諧參數，為了消除式（10）中的久期項，必須使：

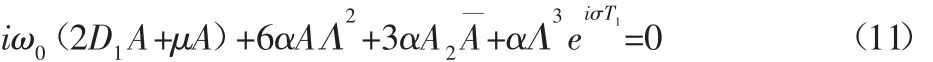
令 A＝a（t）eiθ（t）/2，其中 a（t）和 θ（t）是均為時間變量 t的實函數，將其代入式（11），整理后分離方程的實部、虛部，便可得到冷連軋機振動系統在極坐標下的平均方程：

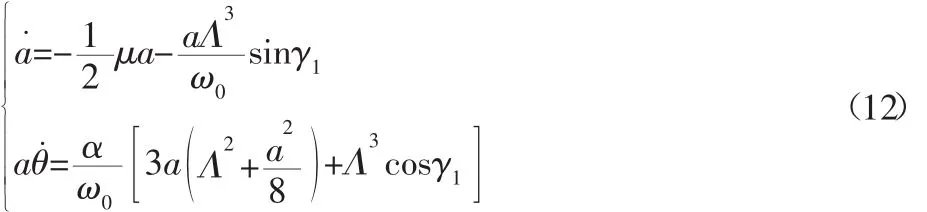
式中：γ1=σT1-θ，對于穩態響應有a˙＝θ˙=0，消去式（12）中的 θ可得動態軋制力下冷軋機系統超諧振動的幅頻特性響應方程為：

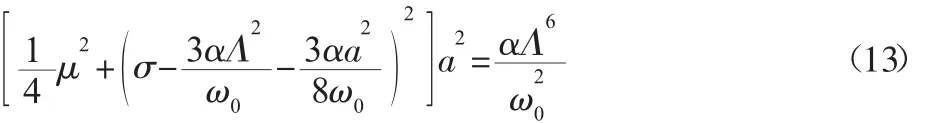
3.2 亞諧共振幅頻特性方程

設ω與3ω0的差別為ε的同階小量，即ω＝3ω0+εσ，σ為調諧參數，為了消除式（10）中的久期項，必須使：

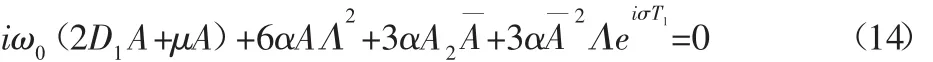
令 A=a（t）eiθ（t）/2，其中 a（t）和 θ（t）是皆為 t的實函數，將其代入式（14），并分離實部與虛部，可得到系統極坐標下的平均方程。

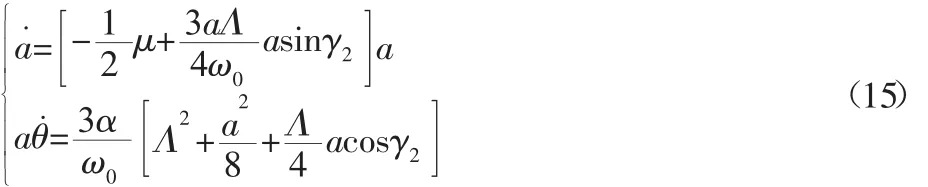
式（5）中 γ2=σT1-3θ，對于穩態響應有a˙＝θ˙=0，消去式（15）中的θ可得動態軋制力下冷軋機系統亞諧振動的幅頻特性響應方程為：

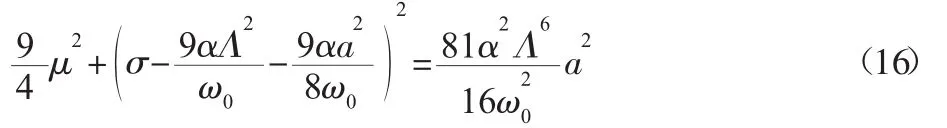
4 超亞諧共振特性分析

以某鋼廠1780型冷連軋機的軋制參數為例，取如下近似值進行仿真計算，分別為：α=2.320，μ=1.225，ω=1.21，F=0.832。

不同軋制參數變化時的冷連軋機超諧共振幅頻特性曲線，如圖3～圖5所示。由圖3可知，隨著F的增大，冷連軋機的振動區域、振動幅值變化較為微弱，可知外激力變化對系統的影響較小，這是由于動態軋制力適時調節，使軋機系統受到的外激力始終保持合適量值，從而避免軋機的劇烈振動，從而驗證了動態軋制力這一概念的有效性。圖4中，隨著線性阻尼μ的增大，系統的振動幅值不斷減小，同時振動區域也不斷縮小，直至系統無振動現象發生，獲得平穩運行，利于生產出高質量、高精度軋制產品。描繪了非線性剛度變化下的系統的超諧共振現象，如圖6所示。隨著參數的增大，共振區域和振幅同時增大，可見，動態剛度系數與動態軋制力組成的非線性參數項的波動對軋機系統的振動影響較大，在實際軋制過程中，要注意控制好這兩項參數的量值，以保證冷連軋機的平穩運行。

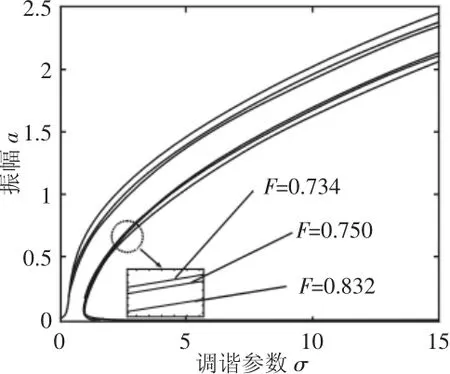
圖3 外激力變化下的超諧共振幅頻響應曲線Fig.3 The Curve of Super-Harmonic Vibration Amplitude-Frequency with Disturb Force

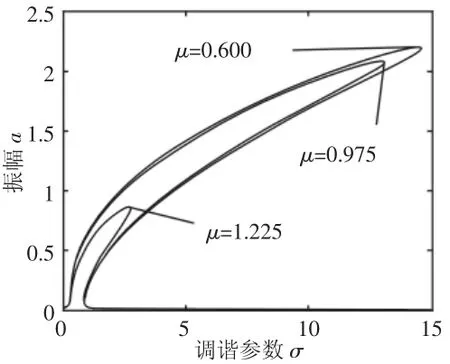
圖4 線性阻尼變化下的超諧共振幅頻響應曲線 Fig.4 The Curve of Super-Harmonic Vibration Amplitude-Frequency with Linear Damping

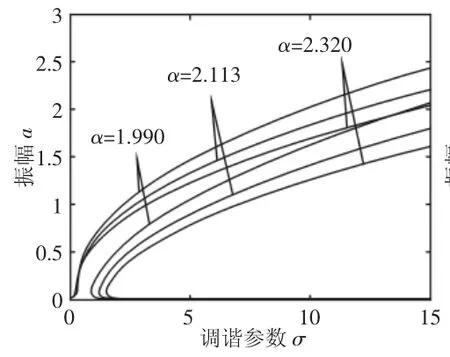
圖5 非線性剛度變化下的超諧共振幅頻響應曲線Fig.5 The Curve of Super-Harmonic Vibration Amplitude-Frequency with Nonlinear Stiffness

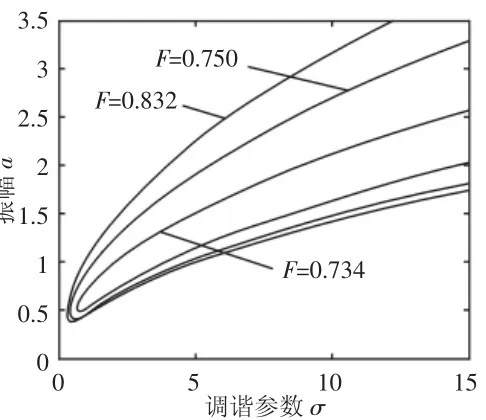
圖6 外激力變化下的亞諧共振幅頻響應曲線 Fig.6 The Curve of Sub-Harmonic Vibration Amplitude-Frequency with Disturb Force

描繪了含動態變化量的外激力、線性阻尼、非線性剛度發生改變時，冷連軋機出現亞諧共振現象的相應特性，如圖6～圖8所示。

圖6中，隨著外激力F的減小，振動幅值減小，共振區域縮小，但變化量較為微小，可見外激力對超諧、亞諧共振的影響一致。圖7中，隨著輥系間阻尼系數的減小，系統的振動幅值不斷增大，同時共振區域也不斷增大，但振動曲線的彎曲程度依然保持不變，即無跳躍現象發生，系統較為穩定。圖8給出了非線性剛度變化下的亞諧共振幅頻特性，隨著α的減小，振幅和共振區域隨之增大，且減小到一定值后，將出現跳躍和突變，使系統發生失穩。

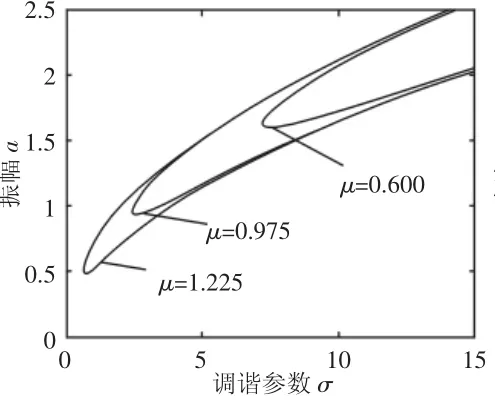
圖7 線性阻尼變化下的亞諧共振幅頻響應曲線Fig.7 The Curve of Sub-Harmonic Vibration Amplitude-Frequency with Linear Damping

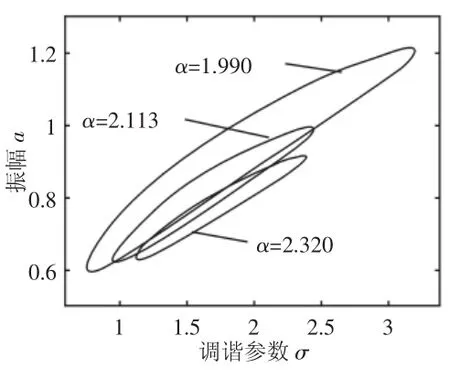
圖8 非線性剛度變化下的亞諧共振幅頻響應曲線Fig.8 The Curve of Sub-Harmonic Vibration Amplitude-Frequency with Nonlinear Stiffness

5 結語

（1）在引入較為接近實際軋制過程中存在動態軋制力的基礎之上，建立了含機械結構、工藝參數以及周期性外激力的冷連軋機非線性振動動力學模型，使軋機振動模型更進一步接近實際振動狀態，豐富了軋機振動模型。應用精度較高的多尺度法，得到了基于動態軋制力下的冷連軋機超諧共振和亞諧共振幅頻特性方程。（2）以冷連軋機振動參數為例，仿真分析了不同軋制參數變化下的冷連軋機超諧、亞諧振動特性，從幅值、共振區域大小、骨干曲線偏移程度等方面給出了抑制軋機振動的措施與參數區域，為軋機平穩運行提供了理論參考。