正則化的加權不完全魯棒主成分分析方法及其在無線傳感器網絡節點軌跡擬合中的應用

孫莞格，夏克文* ，蘭 璞

(1.河北工業大學電子信息工程學院，天津300401; 2.河北省大數據計算重點實驗室(河北工業大學)，天津300401)

(*通信作者電子郵箱19289037@qq.com)

0 引言

無線傳感器網絡(Wireless Sensor Network，WSN)是大量無線傳感器通過自組織的方式而組成的無線網絡［1－2］。在復雜多變的應用環境中，移動無線傳感器網絡需要根據節點的實際移動情況對數據進行采集分析，傳感節點的位置和軌跡信息多次發送會增加網絡的能量消耗。傳感器節點自身的能量有限的，怎樣才能延長WSN的運行時間，是WSN的重點研究問題。

無線傳感器網絡節點的軌跡擬合方法有很多，目前比較普遍的分類方法有基于頻繁路徑的軌跡擬合、基于馬爾可夫模型的軌跡擬合、基于Kalman濾波的軌跡擬合和基于線性回歸的軌跡擬合。這些方法在軌跡擬合方面各具優勢，但仍存在一些問題:前兩種方法計算量大、算法運行時間長［3］;后兩種方法耗時少，但在節點移動軌跡的轉折處或者當數據出現嚴重缺失時出現了失真［4］。

近幾 年，低 秩 矩 陣 恢 復 技 術［5］(Low Rank Matrix Recovery，LRMR)將向量的稀疏表示模型擴展到低秩矩陣中，使它成為繼壓縮感知之后又一個有潛力的處理大規模數據的信號處理方法。低秩矩陣恢復包括魯棒主成分分析(Robust Principal Component Analysis，RPCA)和矩陣補全(Matrix Completion，MC)。馮緒等［6］將矩陣補全應用到無線傳感器網絡節點的軌跡擬合當中，采用稀疏矩陣奇異值分解方法 (Sparsity Rank Singular Value Decomposition，SRSVD)方法把原問題松弛為非凸優化問題，可將目標函數簡化為兩個矩陣的F范數之和，在降低數據采樣比例的情況下仍能有效地對移動軌跡進行恢復。魯寧等［7］對求解魯棒主成分分析的嚴格增廣拉格朗日(Exact Augmented Lagrange Multiplier，EALM)算法進行了粗尋優和細尋優的結合，提出了半精確增廣拉格朗日(Semi-Exact Augmented Lagrange Multiplier，SEALM)算法，提高了求解速度。然而SRSVD方法對稀疏噪聲敏感，SEALM算法在采樣比例小時能準確地擬合。此外，這兩種方法都需要假設不存在高斯噪聲，該假設往往不能嚴格符合實際情況。

為使整個系統在存在高斯噪聲時仍能有效且穩定，本文先將基于魯棒主成分分析和矩陣補全的不完全魯棒主成分分析(Incomplete Robust Principal Component Analysis，IRPCA)方法應用于節點的移動軌跡擬合;再在IRPCA的基礎上進行改進，分別對低秩矩陣和稀疏矩陣進行加權，然后將高斯噪聲矩陣的F范數作為正則項，最后應用于節點的移動軌跡擬合。

1 WSN系統模型

設無線傳感器網絡中有W個節點，每個傳感器節點在相同的時間間隔移動N次，而且要在每次移動之后記錄節點當前的坐標信息。很明顯，隨著節點的不斷移動，要傳輸和存儲的坐標信息不斷增加，無線傳感器網絡系統所消耗的能量也在迅速增多，因為所有節點的坐標信息都要存儲。如果可以通過采樣降低坐標信息的傳輸量，再通過特定的恢復算法對未采樣節點的坐標信息進行恢復，就能夠很大程度地降低坐標信息的傳輸量，從而減少整個系統的能量消耗。

為此，用坐標信息矩陣表示模型［6－7］，如式(1)所示，其中設矩陣X為2W×N階的節點位置信息矩陣，即:

可以很容易地發現，當節點在勻速移動時，矩陣X擁有秩為2，因此該矩陣是一個低秩矩陣。但這僅僅是理想情況，在現實情境中，節點不一定可以以一個固定的速率移動，通常在此處認為它是有規律性的，所以可以判斷出來矩陣X含有低秩性［8］。

為了對節點坐標信息矩陣進行稀疏處理，對矩陣X根據節點的位置進行采樣分析，形成采樣矩陣T，如式(2)與式(3)所示:

令D是經過采樣后測量得到的節點位置信息矩陣，如式(4)所示:

其中“.×”表示矩陣之間的點乘。

在WSN中，可以在真實測量中獲取矩陣D，其中矩陣D只擁有并不完全的節點坐標信息。通過D恢復出原始完整的坐標信息矩陣X就可使用低秩矩陣恢復算法，主要是矩陣補全方法和魯棒主成分分析方法。

1)矩陣補全方法(MC)［9］:當數據矩陣D含缺失元素時，可根據矩陣的低秩結構來恢復矩陣的全部元素。矩陣補全可描述為矩陣核范數最優化問題:

其中:矩陣A為待求解低秩矩陣;Ω為矩陣D采樣元素對應的下標 集 合;PΩ(·) 為 正 交 投 影 算 子; ［PΩ(M)］ij=

對于優化問題式(5)，則可以通過增廣拉格朗日算法解出原始低秩矩陣，比如文獻［6］將矩陣補全應用到無線傳感器網絡節點的軌跡擬合當中，通過SRSVD方法對非凸優化問題進行松弛，把矩陣的秩松弛到矩陣的F范數，并轉化為非約束優化問題，在降低數據采樣比例的情況下仍能有效地對移動軌跡進行擬合。

2)魯棒主成分分析方法(RPCA)［10－11］: 已知矩陣 D，并且D=A+E，其中A和E未知，但先驗信息A是低秩矩陣，E是稀疏矩陣且非零元素可任意大。為刻畫矩陣A的低秩性和矩陣E的稀疏性，可以極小化矩陣A的核范數和矩陣E的l1范數來構造最優化問題:

其中:‖X‖1等于矩陣X所有元素絕對值的和;‖X‖*等于矩陣X所有奇異值的和;λ是低秩矩陣和稀疏矩陣的折中因子。

對于優化問題式(6)，可以通過增廣拉格朗日算法交替更新A和E，即可恢復出原始低秩矩陣。文獻［7］在求解RPCA的EALM算法中對單一低秩矩陣和噪聲矩陣作局部粗尋優，對恢復矩陣元素作全局細尋優，提出了SEALM算法，加快了求解速度。

上述兩種模型均存在各自的缺點，比如SRSVD方法不能準確地處理存在大量稀疏噪聲的情形，EALM算法不能處理采樣比例小的情況。為了彌補兩種模型的不足，使之能夠處理存在大量稀疏噪聲且有大量元素缺失(即采樣比例小)的情況，文獻［12］把RPCA和MC進行了結合，提出了不完全魯棒主成分分析(Incomplete RPCA，IRPCA):

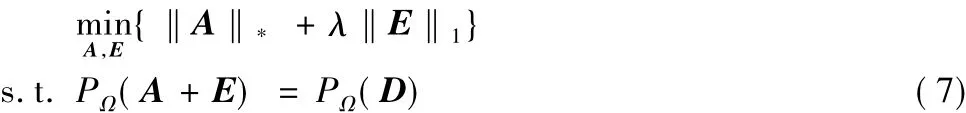
然而實際工作中往往存在高斯噪聲，上述方法均不能有效地抑制高斯噪聲，本文的工作先將IRPCA應用到無線傳感器網絡軌跡擬合，再假設當存在高斯噪聲時，如何改進算法才能有效地通過D恢復出原始完整的坐標信息矩陣X，然后進行軌跡擬合。

2 正則化的加權IRPCA方法

2.1 正則化的加權IRPCA模型的提出

標準核范數平等地對待所有的奇異值，為了更好地刻畫低秩矩陣的低秩性，可對低秩矩陣的奇異值進行加權，較大的奇異值通常包含了較多的信息，應該分配較小的權值以減小閾值收縮幅度，較小的奇異值應該分配較大的權值來增大閾值收縮幅度。同樣地，標準l1范數平等地對待所有的矩陣元素，為了更好地描述稀疏矩陣的稀疏性，對于較大的矩陣元素應該用較小的權值來降低其影響，對于較小的矩陣元素應該用較大的權值提高其影響［13］。為此提出加權的不完全魯棒主成分分析(Weighted IRPCA，WIRPCA)的數學模型:

考慮到在實際環境中往往存在高斯噪聲，用F范數刻畫高斯噪聲作為目標函數的正則項，可對高斯噪聲有較強的抑制作用，擬合效果更加準確和穩定。為此提出正則化的加權不完全魯棒主成分分析(Regularized WIRPCA，RWIRPCA)的數學模型:

2.2 數學模型的求解

式(9)可變形為:

為了變形求解的需要，通過引入n1×n2維實矩陣變量M，模型式(10)可重新表示為:

為求解式(11)改進的RWIRPCA模型，首先要考慮權重ωA和ωE的取值。由于權重的取值與被加權部分成反比［14］，即ωA的取值與低秩矩陣A的奇異值成反比，且ωE的取值與稀疏矩陣E的元素成反比。RWIRPCA的權值更新算法步驟如算法1所示。

算法1 權值更新算法步驟。

輸入 觀測矩陣 D ∈ Rn1×n2，采樣集合 Ω，參數 λ，τ，μ，εA，εE;

輸出 最優解A，E，Z，M。

2) 交替迭代更新矩陣A，E，Z，M。

4) 若迭代收斂或i達到最大迭代次數，輸出最優解A，E，Z，M。

在確定了權值ωA和ωE后，在式(11)中，ωA和ωE相當于常數，接下來可采用非嚴格拉格朗日乘子法(Inexact Augmented Lagrange Multipliers，IALM)對步驟2進行求解，在求解之前先引入兩個定理。

定理1 軟閾值算子［15］:設 G是n1×n2維實矩陣，則優化問題的最優解是X*=Sε(G)，第(i，j) 元素為 max(|gij|－ ε，0)sgn(gij)，其中ε＞0。

定理2 奇異值收縮算子［16］:優化問題min

X{ε‖X‖*+，具有閉解 X*=Dε(G)，其中 Dε(G)=USε(Σ)VT，UΣVT是矩陣G的奇異值分解結果。

采用IALM求解式(11)，其增廣拉格朗日函數為:

其中:μ＞0為懲罰參數;Y∈Rn1×n2為增廣拉格朗日乘子矩陣。

由交替方向乘子法可知，式(12)應用變量交替更新的方式進行迭代求解，其具體過程為:

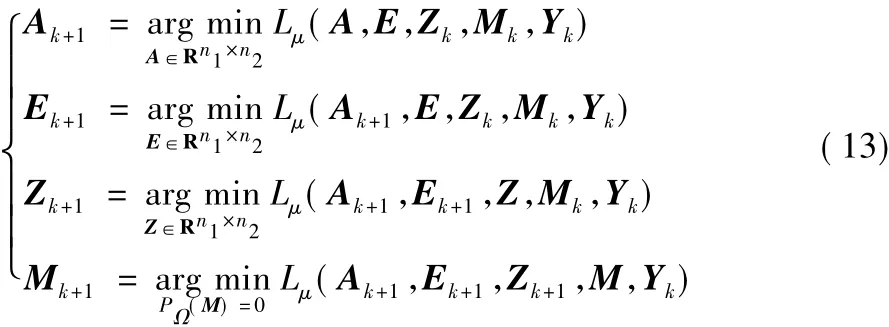
固定 E，Z，M，更新 A:

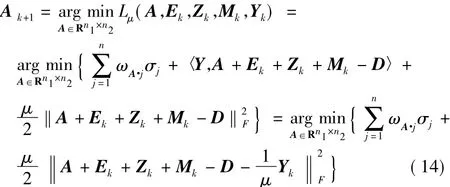
由定理2推理得:

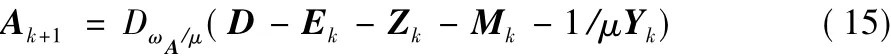
固定 A，Z，M，更新 E:

由定理1推理得:

固定 A，E，M，更新 Z:

對式(18)求導并令導數為0，得:

易得:

固定 A，E，Z，更新 M:

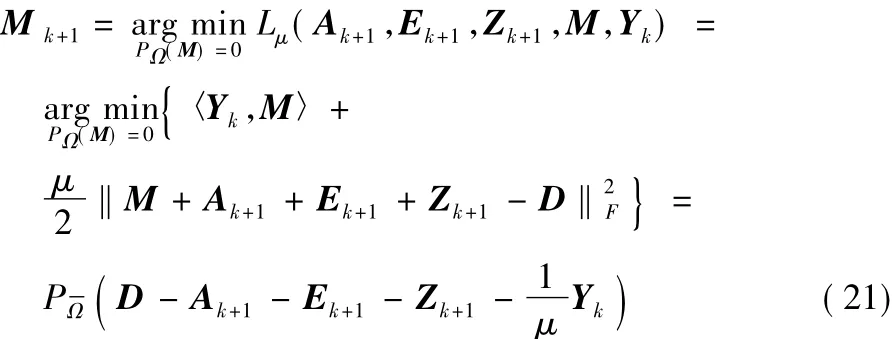
其中Ω表示Ω的補集。

最后更新Y:

按照上述步驟進行交替更新，迭代收斂后可得到式(11)的最優解。算法2給出了IALM算法求解RWIRPCA的步驟。

算法2 IALM算法求解RWIRPCA模型。

輸入 觀測矩陣 D ∈ Rn1×n2，采樣集合 Ω，參數 λ，τ，μ，ωA，ωE;

輸出 最優解A，E，Z，M。

3 實驗結果及分析

本實驗使用Matlab R2014b進行仿真分析，運行環境基于Windows10操作系統平臺，內存8.00 GB，處理器為Intel Core i5 CPU，主頻參數為2.40 Ghz。在式(1)中的位置信息矩陣X中包含了任意節點在任意次移動后的橫縱坐標信息，令(xi，j，yi，j) 作為節點 i在發生了第 j次移動后獲得的橫縱坐標，(^xi，j，^yi，j)為求解得到的估計坐標，坐標信息矩陣估計值 ^X可以提供此節點使用恢復算法得到的橫縱坐標，則可定義矩陣X與^X之間的均方根誤差如式(23)所示:

式中n為觀測次數。

具體實驗流程如圖1所示。

為考察改進的RWIRPCA方法在不同情形下的性能，設計了3組不同的實驗。實驗1考察RWIRPCA方法在采樣比例小且稀疏噪聲大的條件下的擬合效果，實驗2考察RWIRPCA方法在高斯噪聲條件下的擬合效果，實驗3考察RWIRPCA方法在稀疏和高斯混合噪聲條件下的擬合效果。

3.1 實驗1:稀疏噪聲與采樣比例實驗

本實驗假設坐標信息矩陣數據僅包含稀疏噪聲，稀疏噪聲大小為5000 dB～10 000 dB隨機產生，稀疏噪聲比例分別設定為0%、5%、20%這3種。當稀疏噪聲比例分別設定為0%、5%、20%時，圖2顯示了在對原始坐標矩陣進行不同比例采樣情況下 SRSVD方法、SEALM方法、IRPCA方法和RWIRPCA方法擬合誤差的變化情況

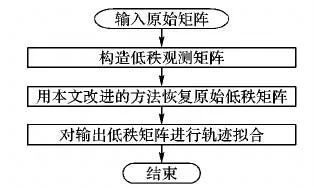
圖1 實驗流程Fig.1 Experimental process

圖2 不同稀疏噪聲比例時，節點軌跡擬合誤差對比Fig.2 Comparison of node trajectory fitting error under different sparse noise ratio

由圖2可以明顯看出，SRSVD在稀疏噪聲條件下效果較差，即使當采樣比例高達80%時擬合誤差仍在0.11以上。SEALM在采樣比例較小時也就是有大量元素缺失時效果較差，即使當稀疏噪聲比例為0時擬合誤差仍在0.20以上。而對于IRPCA和RWIRPCA在稀疏噪聲大且采樣比例較小時仍能取得比較穩定的擬合效果，尤其是RWIRPCA與其他3種方法相比，體現了高度的優越性。

3.2 實驗2:高斯噪聲實驗

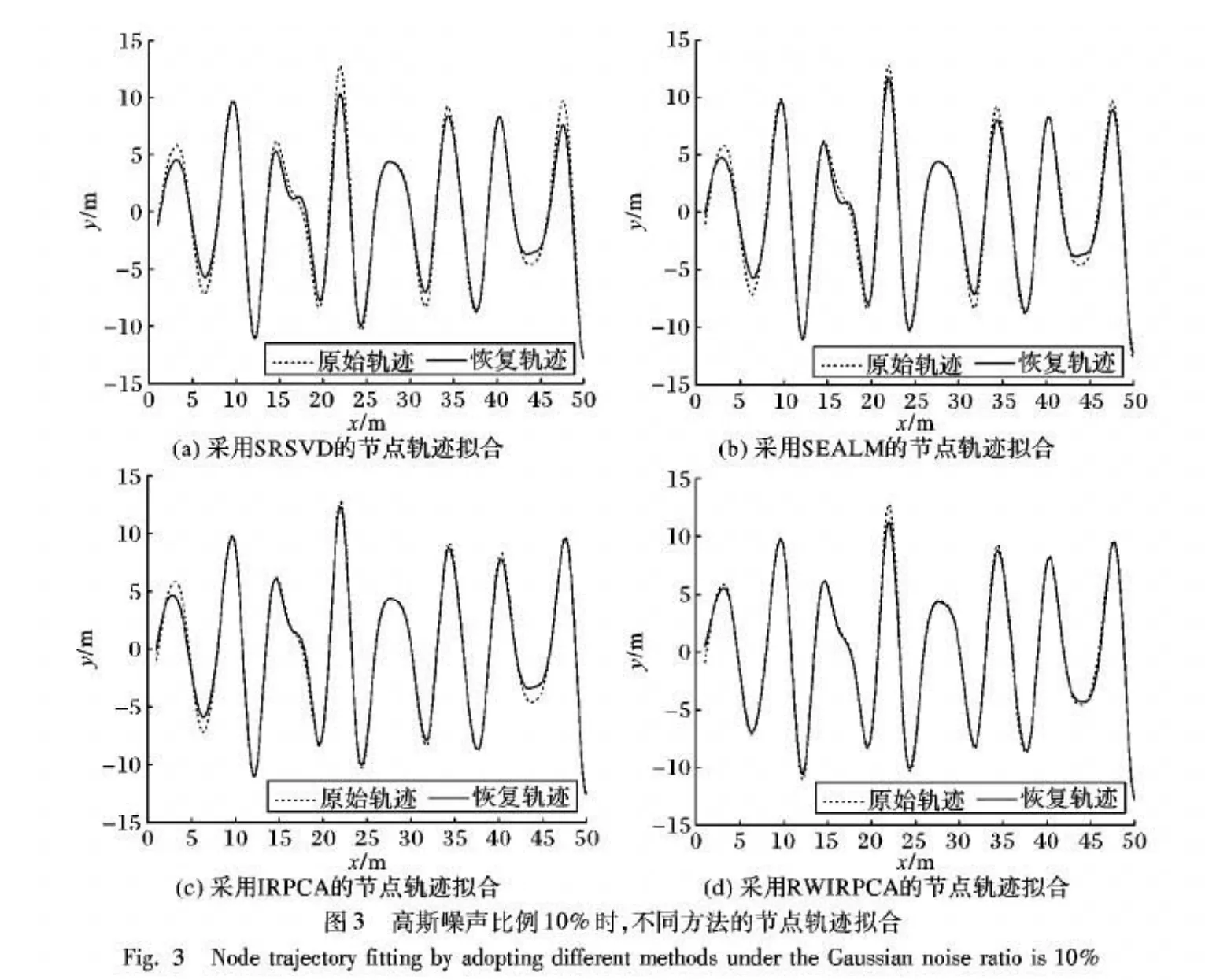
圖4 高斯噪聲比例50%時，不同方法的節點軌跡擬合Fig.4 Node trajectory fitting by adopting different methods under the Gaussian noise ratio is 50%

本實驗假設坐標信息矩陣數據僅包含高斯噪聲，設置其均值為0，標準差為100。在噪聲比例為10%、20%、30%、40%、50%分別采用SRSVD方法、SEALM方法、IRPCA方法和RWIRPCA方法分別進行移動WSN節點軌跡擬合。當噪聲比例為10%和50%時，通過仿真圖來表示第一個移動節點的運行軌跡。圖中節點移動次數為100，網絡覆蓋區域為(0，－15)～(50，15)，其擬合仿真圖形分別如圖3～4所示，圖中x與y分別代表該節點移動的橫坐標與縱坐標。

由圖3～4可以明顯看出，當噪聲比較小時(如高斯噪聲比例為10%)，方法改進前后的擬合效果差距不明顯，但隨著高斯噪聲比例增大到50%時，SRSVD、SEALM、IRPCA出現了明顯的失真，而改進后的RWIRPCA擬合效果仍然保持相對穩定。

為了進一步分析對比采用 SRSVD、SEALM、IRPCA和RWIRPCA優化WSN節點軌跡擬合問題的效果，對仿真實驗的效果通過表格和圖示的方式進行展示與分析。在不同噪聲比例下，4種方法的優化效果比較如表1所示。

從表1中不同的誤差以及運行時間可以看出，SEALM用時最長，SRSVD擬合誤差最大。在IRPCA和RWIRPCA運行時間相近的情況下，就擬合誤差來說，RWIRPCA要比IRPCA低，擬合效果更好。尤其隨著噪聲比例不斷增長RWIRPCA的擬合效果依然優于IRPCA，RWIRPCA的優勢更加明顯;當噪聲比例不斷增大到50%時，IRPCA的擬合誤差高達0.17 m，而RWIRPCA的擬合效果依然保持穩定。從而可知，當外界存在高斯噪聲時，改進的RWIRPCA可以提高移動節點擬合的準確性，從而提高整個無線傳感器網絡的穩定性。

表1 不同高斯噪聲比例時采用不同方法的擬合效果比較Tab.1 Comparison of trajectory fitting results by adopting different methods under different Gaussian noise ratio

3.3 實驗3:混合噪聲實驗

本實驗假設坐標信息矩陣數據包含稀疏噪聲和高斯噪聲，稀疏噪聲大小由5000 dB～10000 dB隨機產生，高斯噪聲均值為0，標準差為100。不同大小混合噪聲比例情況下分別采用IRPCA方法和改進的RWIRPCA方法進行移動WSN節點軌跡擬合誤差的變化情況如圖5所示。

圖5 不同混合噪聲比例時軌跡擬合誤差對比Fig.5 Comparison of trajectory fitting error under different mixed noise ratio

由圖5可以看出，當坐標信息矩陣數據包含不同程度大小的混合噪聲時，與 SRSVD、SEALM、IRPCA相比，改進的RWIRPCA有更低的擬合誤差，擬合效果更好。當混合噪聲逐漸增大時，SRSVD、SEALM、IRPCA的擬合誤差迅速上升，而RWIRPCA的擬合誤差依然保持相對穩定，具有更準確的擬合效果。可見當稀疏噪聲和高斯噪聲同時存在時，RWIRPCA具有更高的擬合精度，在實際應用中更具優勢。

4 結語

在無線傳感器網絡軌跡擬合中，為了降低信息的傳輸量，減少無線傳感器網絡的能量消耗，采用LRMR是切實可行的，然而目前使用的LRMR還存在對噪聲敏感、大量元素缺失時擬合精度差等問題，為此需研究改進的LRMR模型方法。

為此，本文提出了一種改進的正則化加權IRPCA方法，即在IRPCA基礎上矩陣先進行范數加權，然后加入噪聲矩陣的F范數作為正則項。不同比例的稀疏噪聲、高斯噪聲和混合噪聲的詳細實驗與結果對比表明IRPCA和RWIRPCA都可處理采樣比例小且稀疏噪聲大的情況，而RWIRPCA在擬合效果上更具優勢。尤其當存在高斯噪聲或混合噪聲時，RWIRPCA的優勢更加明顯，在擬合效果和誤差上遠遠優于SRSVD、SEALM和IRPCA，將其應用到無線傳感器網絡節點軌跡的擬合當中可以更方便地管理移動節點，減少頻繁傳輸節點的位置和軌跡信息帶來的能量消耗，從而使整個無線傳感器網絡系統更加穩定、更加節能。