基于能力譜法的橋墩橫向抗震性能評價

臧 博

（山西省交通科學研究院，山西 太原 030006）

0 引言

傳統的抗震設計采用基于結構承載能力的方法，例如89抗震規范[1]，其設計理念為“一水平設防，一階段設計”，即只進行彈性抗震設計。為了應對較強的地震，采取加大構件截面和增加配筋的手段以提高其抗力。截面越大，剛度就越強，對于大部分結構來說，其后果就是地震力進一步增大，如此就陷入了惡性循環。

近年來，有學者提出基于性能的抗震設計思想[2]。公路橋梁抗震設計細則[3]的“兩水平設防，兩階段設計”理念，也體現了這種思想。在第二階段抗震設計（延性抗震設計）中引入了“能力保護設計”概念，并且在求取排架墩橫向位移時推薦使用非線性靜力分析法（Pushover）。

Pushover結合能力譜法可以簡單方便地評估結構抗震性能。能力譜最初是由Freeman等人提出，經過不斷改進，現已作為美國應用技術委員會推薦的抗震性能評估方法[4]。該方法在建筑結構中已經得到廣泛應用，而在橋梁結構中應用還比較少。本文采用Pushover和能力譜法，結合工程實例進行橫向抗震性能研究。

1 Pushover基本原理

Pushover是一種靜力彈塑性分析方法，其基本思路是逐步增大對結構施加的側向荷載，使結構直至倒塌或者達到目標變形狀態，用以研究結構在非線性狀態下的性能，考察其變形能力能否滿足要求。

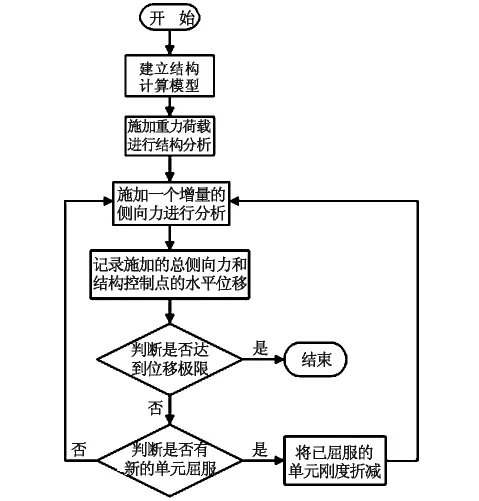
圖1 Pushover分析流程圖

1.1 基本假定

對于以第一振型為主的常規結構，可用等效單自由度體系對結構進行模擬，同時假定結構的形狀向量{Φ}保持不變。

1.2 側向荷載分布模式

采用Pushover方法評價橋梁結構的抗震能力時，應對結構采取合理的側向荷載分布模式。為精確地得到結構地震響應，通常采用與結構的第一振型相似的分布模式，主要有如圖2中幾種形式。

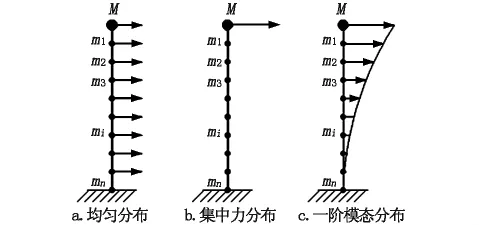
圖2 Pushover加載模式

在實際運用過程中，可以采取均勻分布模式來估計結構地震反應的上限，采取集中力分布模式來估計結構反應的下限[5]。

2 能力譜法

單純地推倒分析并不能得到地震響應值，還需要結合能力譜法以確定結構在指定地震強度下的反應值。本文使用能力譜法，即將地震需求曲線和結構能力曲線繪制在同一坐標系，以評估結構的地震響應。

由于能力曲線一般采用荷載-位移格式，而需求曲線（阻尼比5%的彈性反應譜）一般采用擬加速度-周期格式，二者無法直接比較。需要通過一定的方式轉換為統一的AD格式，即能力譜和需求譜，二者的交點即為性能點。

2.1 能力譜的轉換

由Pushover得到結構的底部剪力-頂部位移曲線（Vb，u），按照式（1）、式（2）轉換為能力譜（Sd、Sa）：

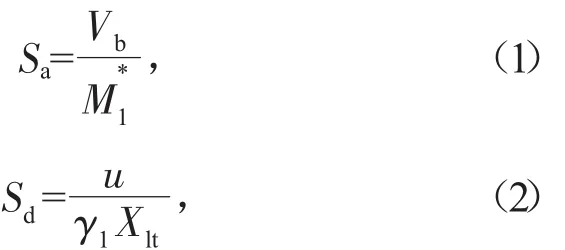
2.2 需求譜的建立

規范一般給出的是阻尼比5%的彈性反應譜（T，Sa），按照式（3）轉換為需求譜（Sd、Sa）：

本文采用延性比法折減彈性需求譜以得到彈塑性需求譜，具體參數參照文獻[6]推薦的Vindic關系模型：

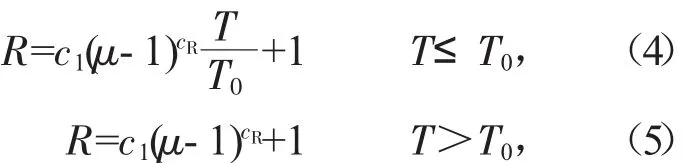
式中：Tg是特征周期；c1、c2、cR、cT等參數取決于結構的滯回性能和阻尼比，參數取值見表1。

表1 Vindic模型參數

按照上述方法，結合本橋的地震動參數（Tg=0.45 s，Ⅱ類場地），將公路橋梁抗震細則規定的E2地震設計反應譜轉換為需求譜，如圖3所示。

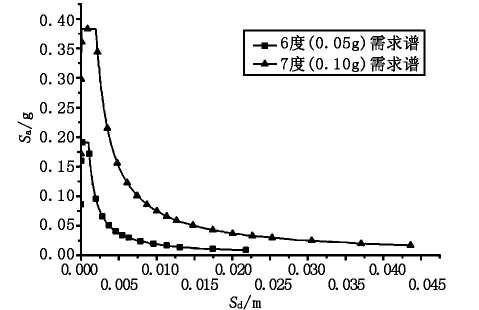
圖3 橋位處不同烈度的需求譜曲線

2.3 求取性能點

ATC-40中給出了計算目標位移的迭代計算方法，具體如下：

a）假設譜位移 Di=(Te，ζ)，其中 Te是結構的基本周期，ζ是阻尼比，取0.05。

b）根據能力譜屈服位移Dy，計算延性系數μ=Di/Dy。由μ計算得到等效阻尼比ζeq。

c）根據等效阻尼比ζeq，將彈性反應譜折算作為需求譜。并將Pushover分析所得能力譜與需求譜相疊加，交點處對應的位移即為譜位移Dj。

d）若Di、Dj誤差不超過5%，則目標位移等于Di。否則令 Di=Dj，重復 b）～d）。

3 算例分析

3.1 計算分析模型

晉蒙黃河大橋引橋采用三柱式橋墩，本文選用其中一個具有代表性的橋墩：蓋梁高2.2 m，墩凈高21 m，柱徑1.6 m，樁徑1.8 m，墩柱采用C35混凝土，樁基采用C30混凝土，縱筋采用32Φ28 mm，箍筋選用φ10@100/150 mm。采用Midas軟件進行計算Pushover分析，蓋梁、系梁、墩柱、樁基均用梁單元模擬，樁側土體等效為土彈簧，彈簧的剛度通過“m法”計算，墩柱上下端設置塑性鉸。計算模型如圖4所示。

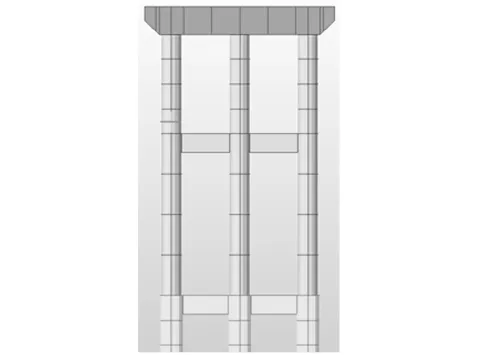
圖4 計算分析模型

3.2 Pushover分析能力曲線

本文在1.2節所述的側向力加載模式中，選擇集中力分布、均勻分布、一階模態分布3種模式，對結構進行Pushover分析，以使分析結果盡可能地接近真實地震響應。將得到的底部剪力-頂部位移曲線，結合動力特性分析得到的基本振型、參與質量、參與系數，按2.1節所述的方法轉換為能力譜。如圖5所示。

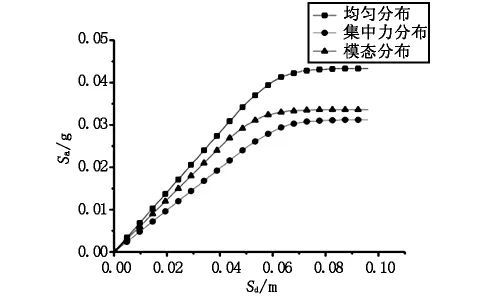
圖5 橋墩不同加載模式下的能力譜曲線

由圖5可以看出，在本文所采用的3種加載模式下，結構的能力譜曲線變化趨勢較為一致。其中，集中力分布和一階模態分布的譜加速度較為接近（也即屈服剪力較為接近），均勻分布和集中力分布的譜位移較為接近（也即屈服位移較為接近）。

3.3 性能評價

按照2.3節的迭代方法求得的能力譜與需求譜的交點，就是結構在于地震作用下的性能點，意味著結構的最大非線性承載力和最大位移。該點在目標性能控制范圍內，則表示該結構能夠滿足性能要求。將不同加載模式下能力譜與需求譜的交點列于表2，并給出對應的墩底剪力和墩頂位移。

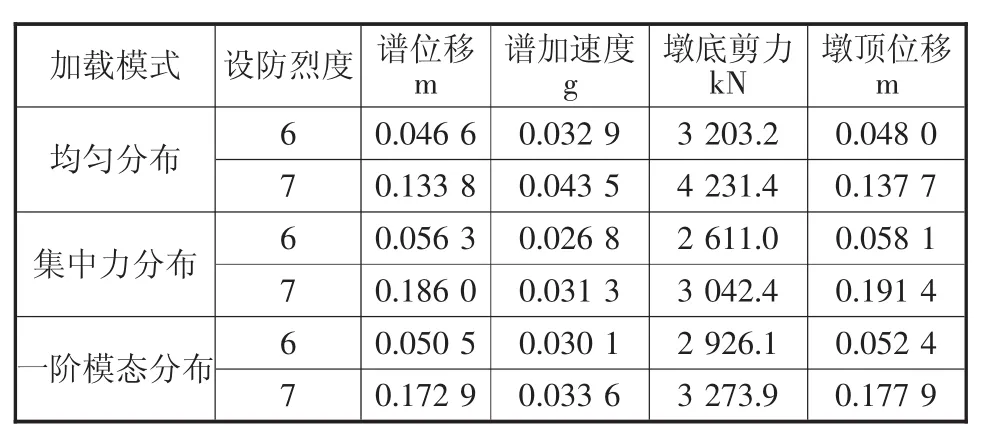
表2 橋墩橫向響應值（規范反應譜）

需求譜曲線與各加載模式下的能力譜曲線均存在交點，表明結構可以抵抗6度、7度設防地震強度，且結構在6度設防地震烈度下處于彈性狀態。從表2中的剪力、位移來看，在6度設防地震烈度下，各加載模式下的墩底剪力和墩頂位移相差不多；而7度設防地震烈度下，集中力分布和一階模態分布下的墩底剪力和墩頂位移較為接近。

4 結論與展望

本文介紹了Pushover分析的基本原理和應用方法，采用能力譜法評價了實際工程中橋墩結構的抗震性能。分析結果表明：

a）均勻分布、集中力分布兩種側向力加載方式可以估計結構能力譜的上、下限。

b）算例結構可以抵抗6度、7度設防地震強度，且在6度設防地震烈度下結構處于彈性范圍內。

由于篇幅所限，文中僅對結構一個方向的抗震性能進行了簡單評價，而實際地震運動則是多維的、往復的，如何將Pushover分析方法推廣到多維地震下結構抗震性能評價中，將是一個值得研究的課題。