機車轉子非線性系統的動力學分析
楊 柳, 楊紹普, 楊月婷
(1.北京交通大學 機械工程學院,北京 100044;2.石家莊鐵道大學 機械工程學院,石家莊 050043)
工程中受復雜激勵作用下,機車雙轉子傳動系統動態分析是機車運行狀態和疲勞強度的關鍵。尤其是在機車高速運行中,出現的軸承及齒輪故障會對機車運行帶來很大的安全隱患。所以如何準確建立非線性轉子動態模型及檢測轉子的振動成為分析的關鍵。
機車雙轉子系統由輪對齒輪、軸承及主、從轉軸組成。最初,Jeffcott轉子系統,經常被用作研究大型柔性轉子結構模型,系統穩定性、臨界轉速和動態特性[1-3]。Jeffcott[4]最早提出并分析了轉子動力學單自由度模型。并研究了在超臨界運行時,轉子具有自動定心現象。之后,Cveticanin[5]建立了Jeffcott 轉子的二階撓度函數的非線性微分方程,并對Jeffcott轉軸進行了穩定性分析。Ishida等[6]利用Jeffcott轉子模型,出現2倍轉頻時,分析系統非線性分岔特性及內共振現象。隨著工業發展,對稱轉子系統軸-齒輪-軸承耦合系統分析是成為研究重點[7]。轉子系統的特性研究主要從以下幾個方面,首先,對柔性轉子穩定性及臨界轉速的研究。其次,不平衡質點對幅值和相位角的影響。Dimentberg[8]是第一個給出簡支撐邊界條件下,考慮轉軸質量,轉子齒輪耦合系統的動態方程。魏靜等[9]建立高速機車齒輪傳動系統彎扭耦合多自由度動力學模型,定量分析了齒輪內部激勵、齒面間隙、軸承游隙等參數等對高速機車齒輪傳動系統的影響。Eshleman等[10]研究了軸承黏彈性條件下,彈性轉軸的臨界轉速求解及幅值響應分析。唐進元等[11]建立了含齒側間隙和徑向間隙的動力學模型,著重分析研究了齒輪系統的混沌和分岔現象。竇唯等[12]針對實際高速齒輪轉子系統,建立了考慮齒輪嚙合及扭轉共同作用的彎扭耦合非線性振動模型,研究了偏心量、齒輪嚙合剛度等參數對系統振動響應的影響規律。Luczko[13]建立鐵木辛柯模型,分析了軸轉子動力學響應。Shiau等[14]求解了復合支撐條件下,旋轉軸的臨界轉速。而對于雙轉子系統的動力學的研究,主要從利用有限元模方法分析雙轉子軸承系統,求解其臨界轉速及模態變形[15-16]。其中,Gupta等[17]采用傳遞矩陣法計算雙轉子系統的臨界轉速和振型, 分析軸承剛度和阻尼系統響應。
以上文獻研究可以看出,現有轉子動力學模型大多數只是考慮轉子質量的影響,而忽略了支撐軸承、嚙合剛度等非線性因素的影響,對考慮齒輪-轉軸-軸承傳動系統的非線性振動模型的較少。本文在前人基礎上,研究了復合邊界條件下,考慮轉軸質量的動力學模型,并綜合針對軸承、輪軌激勵、齒輪嚙合剛度的基礎上,建立了傳動系統的非線性雙轉子動力學模型,求解了其臨界轉速,不同轉速下固有頻率、輪軌接觸力及齒輪剛度等非線性參量變化對傳動系統動力學特性的影響。
1 動力學模型
考慮隨機輪軌激勵,輪對剛性支撐,軸承-齒輪嚙合剛度等條件下,機車非線性雙轉子軸的動力學模型,如圖1所示。
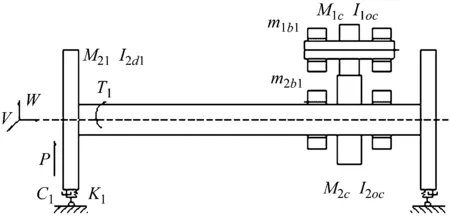
圖1 機車轉子軸模型
轉子系統非線性動力學模型如圖1所示,在該模型中,假設兩輪對彈性支撐,考慮軸承及齒輪等參數的影響。圖1中:T1為轉子扭矩;m1,m2為軸承及M2c,M1c大小齒輪質量;M2i為左右輪對質量。Ω為輸入轉動角速度;I1j,I2d2,I2oc,I1oc分別為軸箱軸承、輪對、大小齒輪轉動慣量;c,k(t)分別為輪齒嚙合阻尼、剛度;w1,v1,w2,v2分別為主、從動軸橫向及其縱向彎曲位移變形量;θ1,θ2分別為主、從動扭轉位移變形量;I1o,I2o分別為主、從動軸極轉動慣量;I1d,I2d分別為主、從動軸轉動慣量;A1,A2分別為主、從動軸截面面積;E,G分別為彈性模量、剪切模量。
建立系統非線性動力學模型,綜合考慮轉子質量及其轉動慣量,齒輪及輪對的集中質量和轉動慣量在復合邊界支撐下系統動能及勢能。
轉子動能
齒輪動能
(3)
輪對動能
(4)
系統勢能
(5)
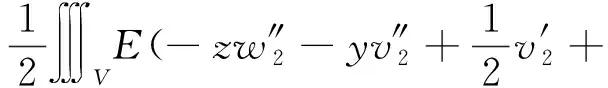
(6)
系統嚙合剛度及其阻尼作用能量
(7)
式中:K(t)為齒輪嚙合剛度;Cc齒輪嚙合阻尼系數;r1,r2為主從動齒輪的基圓半徑。
邊界軸承
軸承剛度、及阻尼剛度對系統影響
(10)
式中:K1b,K2b為主從動軸支撐軸承剛度;c1b,c2b為主從動軸支撐軸承阻尼系數;l1,l2為主動軸及從動軸長度。
外力勢能
(11)
機車垂向平面內,車輛與軌道之間的耦合作用下, 通過輪軌接觸實現運動。輪軌垂向作用力由著名的赫茲非線性接觸理論[18]
式中:G為輪軌接觸常數;δw2(t)為輪軌相對變形量,選取軌道變形量為零;P(t)外載荷。
根據Hamilton最小勢能原理

(12)
將式(1)~式(11)代入得主動輪軸動態方程
mΩ2(ezsinΩt-eycosΩt)
(13)
Kc[δ(x1c)(w1(x,t)+r1θ1)-
δ(x2c)(w2(x,t)-r2θ2)-e(t)]=
mΩ2(ezcosΩt-eysinΩt)
(14)
-Teδ(xe)-r1K(t)[δ(x1c)(w1(x,t)+r1θ1)-
δ(x2c)(w2(x,t)-r2θ2)-e(t)]
(15)
從動輪軸動態方程
(16)
-Tfδ(xr)-r2K0[δ(x1c)(w1(x,t)+r1θ1)-
δ(x2c)(w2(x,t)-r2θ2)-e(t)]
(17)
K0[δ(x1c)(w1(x,t)+r1θ1)-
δ(x2c)(w2(x,t)-r2θ2)-e]=
mΩ2(ezcosΩt-eysinΩt)+δ(xk)P(t)
(18)
式中:P(t)為輪軌激勵;e為偏心距;K(t)為齒輪嚙合剛度,利用Fourier級數展開嚙合剛度為
K(t)=k0+a1cosΩt+b1sinΩt
(19)
邊界條件
主傳動動軸承支撐下
(20)
(21)
從動傳動軸簡支撐下
(22)
(23)
2 動態方程化簡
將上列公式代入式(13)~式(23)。
主動輪軸動態方程
(24)
(25)
δ(x2c)(w2(x,t)-r2θ2)-e]
(26)
方程系數
從動輪軸動態方程
(27)
(28)
-T負載δ(xr)+T′[δ(x1c)(w1(x,t)+r1θ1)-
δ(x2c)(w2(x,t)-r2θ2)-e(t)]
(29)
方程系數
邊界條件
主傳動軸簡支撐下
(30)
(31)
從動輪傳動軸邊界
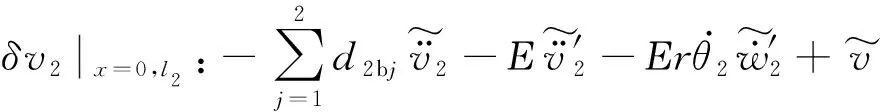
(32)
(33)
方程系數
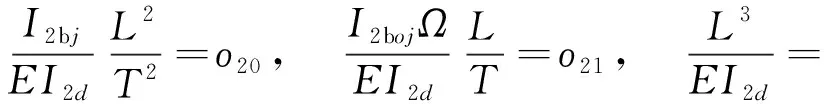
3 臨界轉速及固有頻率
令方程
z1(x,t)=φ1(x)eiωti+φ1(x)eiωt
z2(x,t)=φ2(x)eiωti+φ2(x)eiωt,θ1(x,t)=ψ(x)eiω1t
代入式(24)~式(29),其中ε項為零。
主動輪軸模態方程
(34)
滿足的邊界條件
(35)
從動輪軸模態方程
(36)
滿足的邊界條件
(37)
由式(34)得,主動軸模態方程的通解
(38)
(39)
其中系數為
(40)
其中,主動軸扭轉角邊界條件可知
(41)
將式(38),式(40)代入主動軸彎曲模態邊界條件式(35)中,其中:c1,c2,c3,c4為任意常數項,滿足
(42)
式(42)detΔ=0是關于ω的超越方程,有無窮多個解,求解其方程根問題,不能簡單利用迭代求解,本文采用區間分段法,求解超越非線性方程根問題。如圖2所示,其中,Ω的取值將不直接影響固有頻率的大小,主動軸前三階臨界轉速42, 258,577。
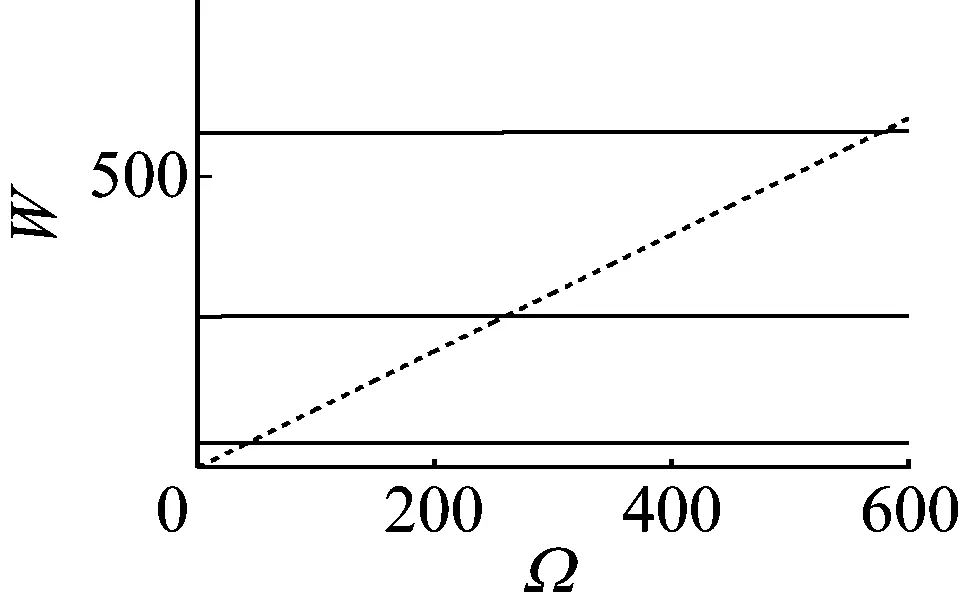
圖2 機車主動軸臨界轉速
由式(36)得,從動軸模態方程的通解
(43)
(44)
其中,
(45)
由從動軸扭轉角邊界條件可知
(46)
將式(43)、式(45)代入從動軸彎曲模態邊界條件式(37)中,求取c21,c22,c23,c24方程矩陣detΔ2=0,式中是關于ω的超越方程,有無窮多個解,采用與上式同一解法。其中,系統參數選定下,轉速Ω改變,轉子系統固有頻率的大小如圖3。圖中數值結果表明,低價固有頻率的大小受轉速影響較小。隨轉速Ω的增大高階固有頻率緩慢增加。系統前三階臨界轉速值為:12.6,43.8,86.5。
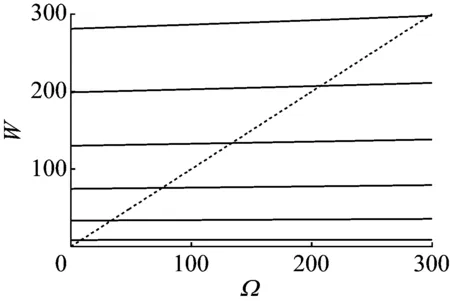
圖3 機車從動軸臨界轉速
當Ω=ω臨界轉速發生時,求取系統機車前三階模態,如圖4~圖6所示,主動軸耦合模態值相對較小,從動軸耦合模態值變化明顯。低階模態值較大,隨著模態階數增加,模態值減小。
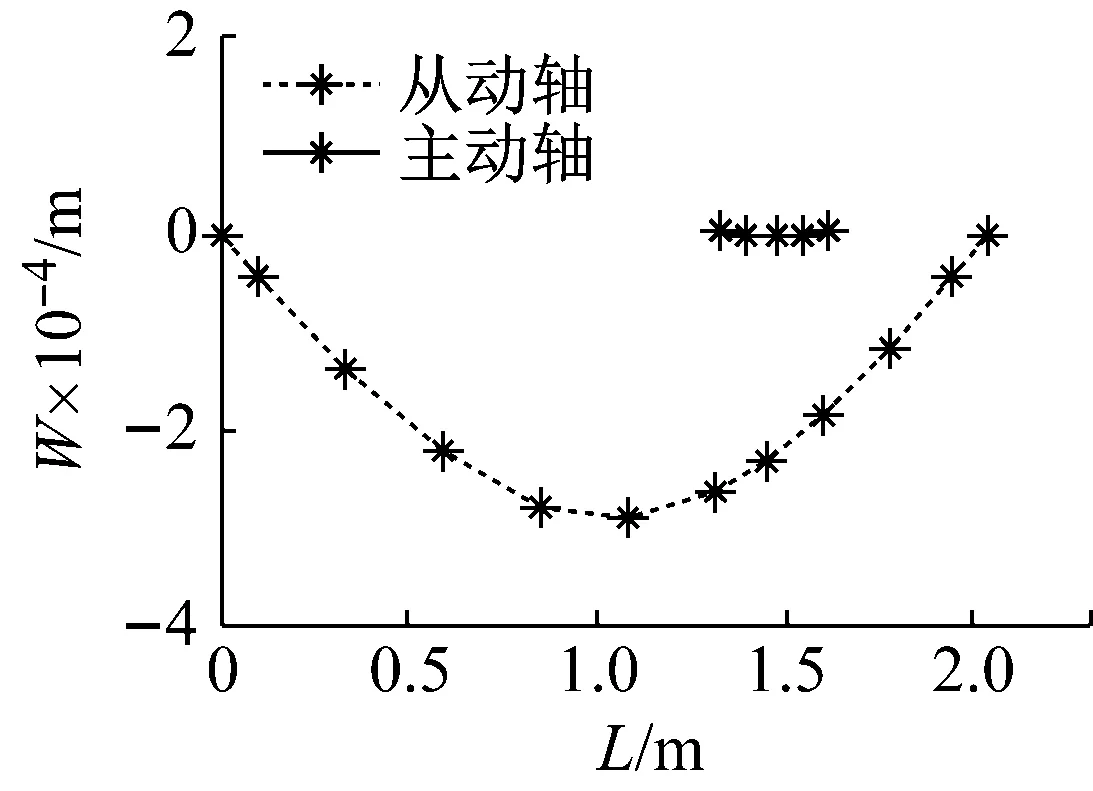
圖4 一階模態分析

圖5 二階模態分析
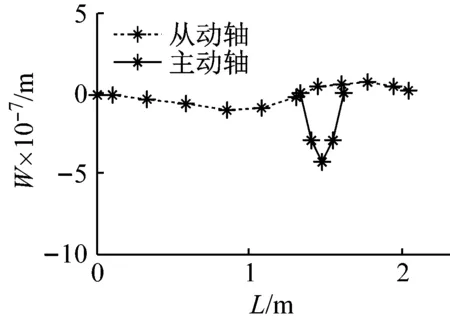
圖6 三階模態分析
4 系統方程化簡
利用Galerkin方法,離散非線性偏微分方程,試探函數選取前一階模態形函數。
令方程
(47)
代入式(24)~式(29)中,方程微分方程中乘以φ1(x),φ1(x),并在區間內積分得
系統主動軸動態方程簡化為
Fr+Ff
(48)
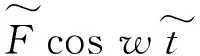
(49)
(50)
系數如下所示
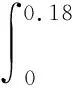
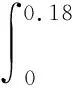
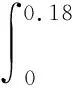
χ6=β1cη14
系統從動軸動態方程簡化為
(51)
(52)
(53)
系數如下所示
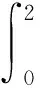
5 數值分析
5.1 時頻響應
機車轉子系統中齒輪嚙合和軸承支撐都是非線性影響因素,整個系統為較復雜的非線性多維方程,因此不必要進行解析求解,在此通過MR-K線性迭代法求解非線性機車雙轉子系統。本文根據機車CRH輪對轉子作為研究對象,給定系統參數:支撐軸系長度為L=2 000 mm,軸截面外徑R=200 mm,內徑為:r=55 mm,車輪質量m=305 kg,集中慣性質量Io1=18.75 kg·m2,齒輪模數ma=6 mm,齒數z1=34,z2=84,齒寬b=70 mm,齒輪的平均嚙合剛度Km。
機車轉子受齒輪嚙合剛度及軸承剛度阻尼、軌道激勵作用下,系統響應和頻域分析分別如圖7~圖12所示。取Ω=ω時,圖7時間幅值響應可知,主軸轉子縱向振動較小,振動頻率成分較多。幅頻響應可知,頻率f1=2.1 Hz及f2=4 Hz時,出現較大的主軸縱向峰值變化。其中,f1為系統一階固有頻率值,而f2為嚙合頻率。圖中,f3=8.3 Hz及f4=9.2 Hz二倍周期頻率值時幅值出現較大變化。圖8時間幅值響應可知,主軸轉子橫向振動較大,齒輪嚙合剛度影響下,響應峰值變化較明顯。幅頻響應中,系統頻率f1及f2時,出現明顯主軸橫向峰值變化。圖9時間幅值響應可知,從動軸轉子縱向振動較小,振動比較單一。幅頻響應圖中,頻率f5=1.2時,受輪軌隨機激勵作用,幅值有明顯變化。圖10時間幅值響應可知,受嚙合剛度影響下,系統從動軸轉子橫向振動較大。幅頻響應圖中,固有頻率f1時,響應幅值較大。圖11響應可知,主動軸扭轉角頻率成分較多,響應變化較大。圖12從動軸扭轉轉子橫向振動較大。幅頻響應圖中,齒輪嚙合頻率f2時,響應幅值較大。
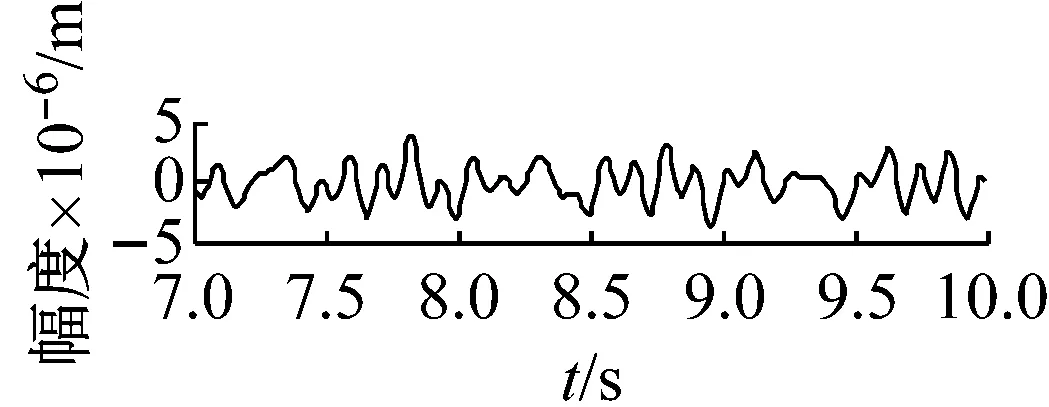
(a) 主動軸v向時程響應
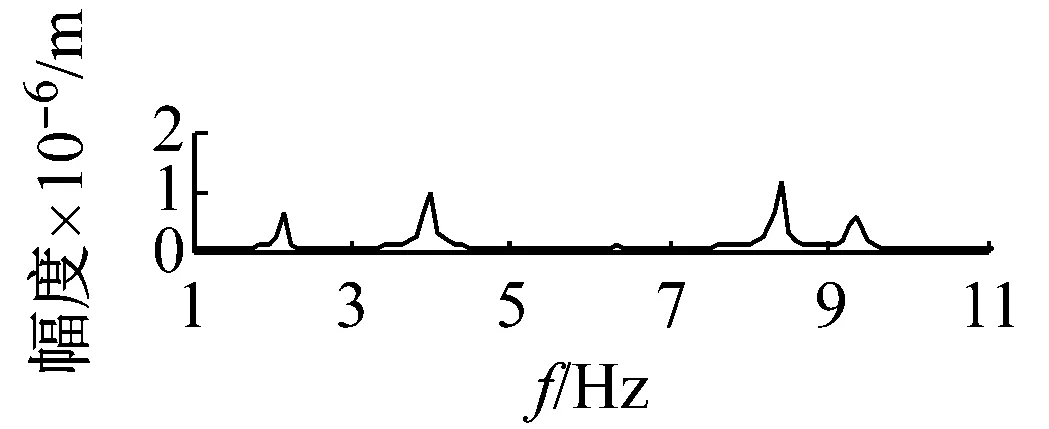
(b) 主動軸v向的頻譜圖
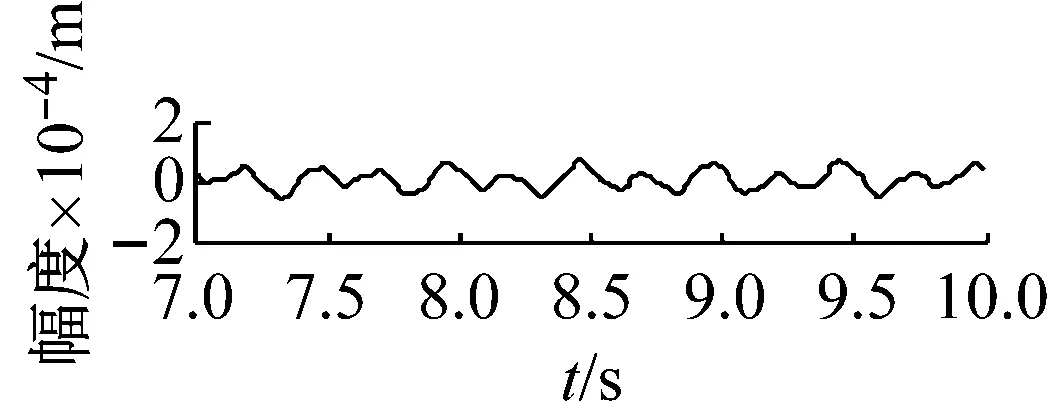
(a) 主動軸w向時程響應
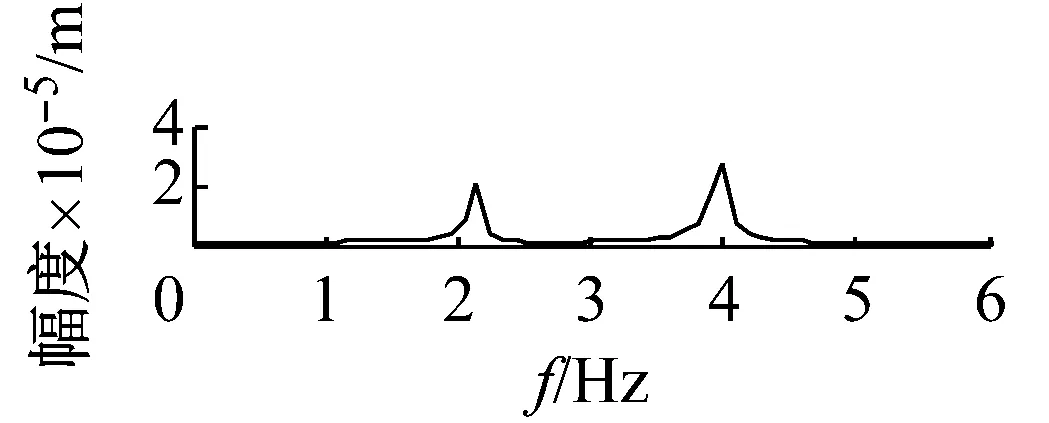
(b) 主動軸w向的頻譜圖
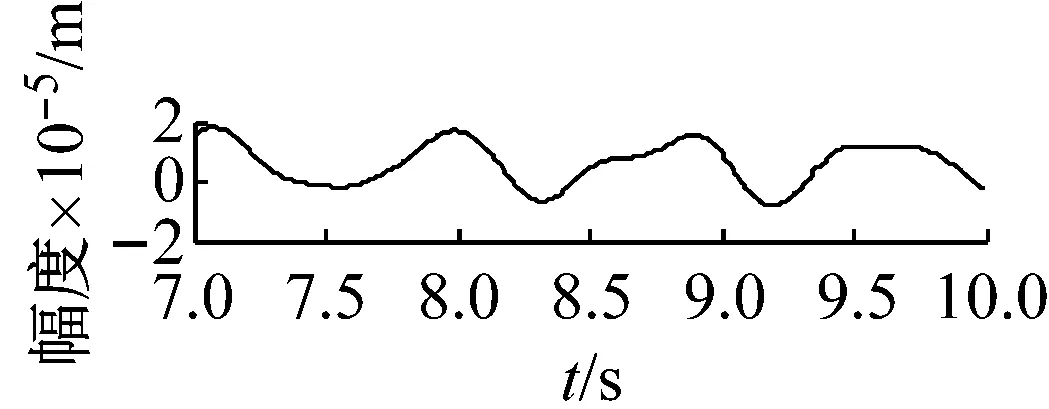
(a) 從動軸v向的時程響應
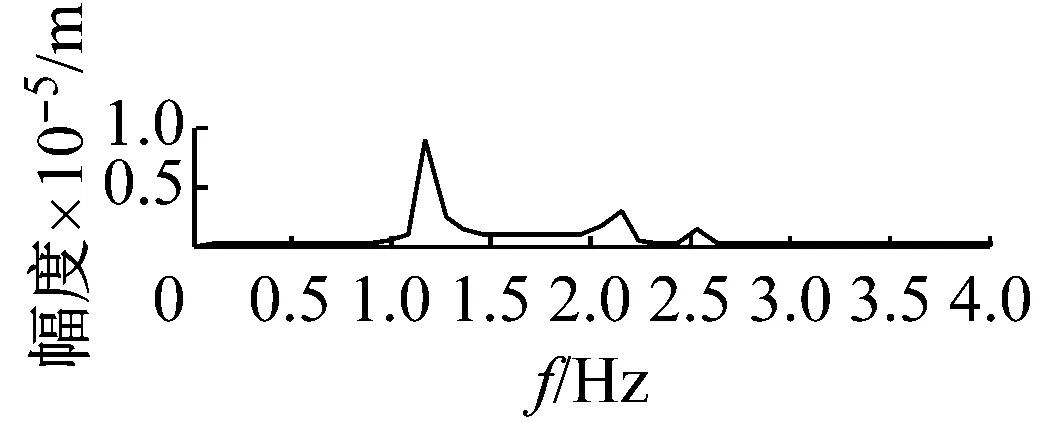
(b) 從動軸v向的頻譜圖
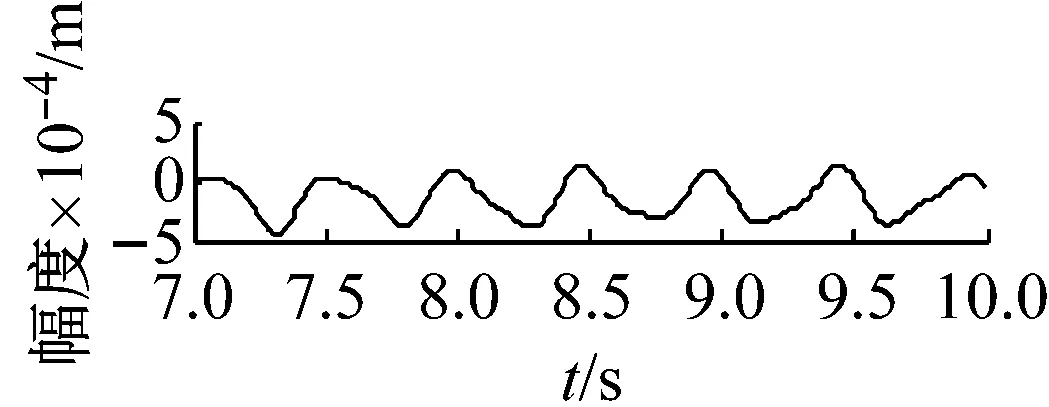
(a) 從動軸w向的時程響應
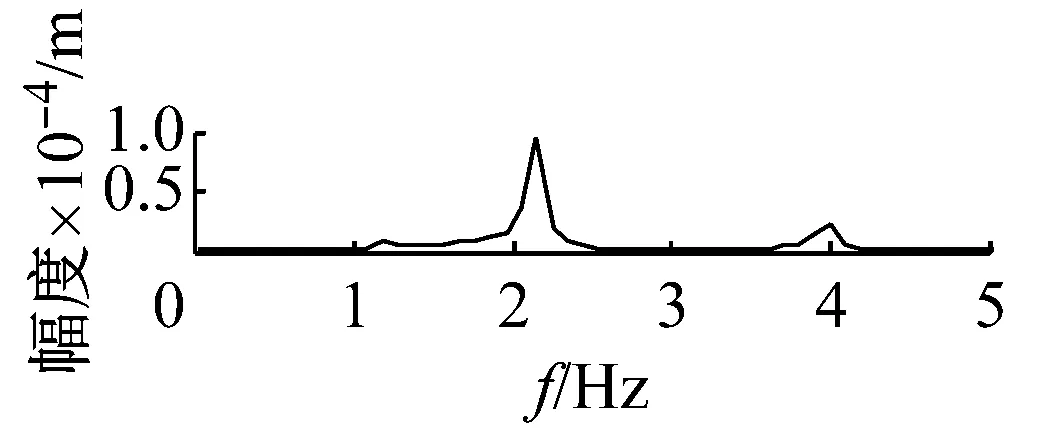
(b) 從動軸w向的頻譜圖
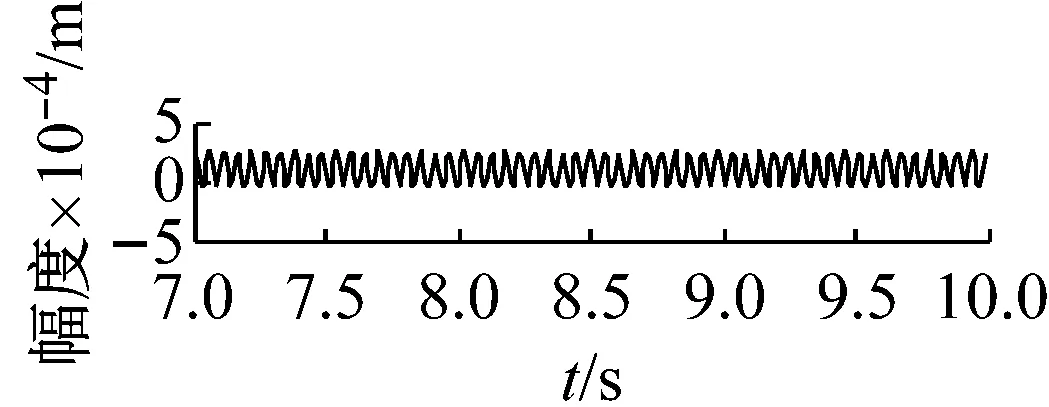
(a) 主動軸扭轉角時程響應
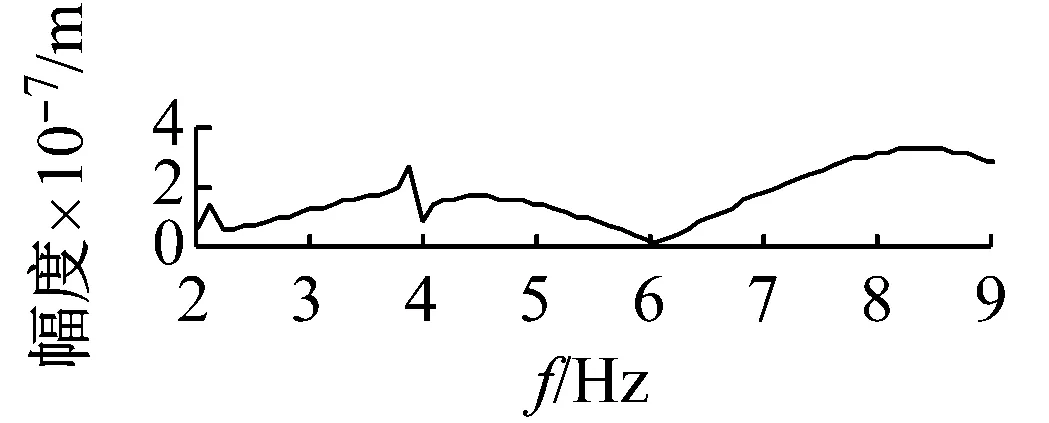
(b) 主動軸扭轉角的頻譜圖
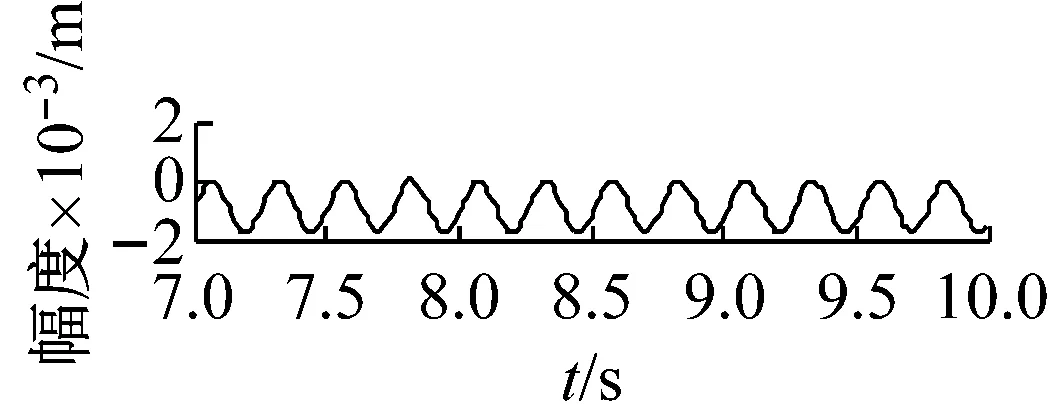
(a) 從動軸扭轉角時程響應
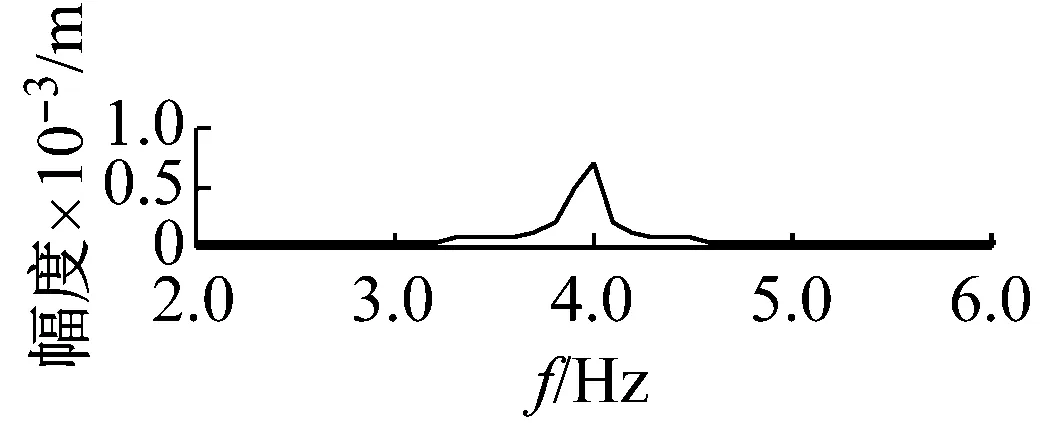
(b) 從動軸扭轉角的頻譜圖
5.2 參數影響及幅頻響應
機車在齒面磨損及點蝕破壞下,齒面均勻磨損變化較小,點蝕面更容易引起嚙合剛度的變化。由其早期齒面磨損對嚙合剛度影響不大,產生的振動激勵很小。這里,選取齒面產生12%的點蝕時,嚙合剛度變化約為6%[19]。圖13和圖14中,由于點蝕作用下齒輪嚙合剛度增大,系統一階固有頻率右移,主動軸響應值增大。圖15和圖16中,點蝕減小,從動軸縱向響應向右移、幅值較小,橫向幅值變大。圖17和圖18中,點蝕導致主動軸固有頻率處出現較大變化,對從動軸振動影響較小。
由圖19中可知,式(53)中輪軌激勵P的增加,主軸轉子的幅值開始呈速減小趨勢,達到一定值時系統幅值受輪軌激勵影響較小。圖20中,當輪對磨損及扁疤時,輪軌激勵P的增加,從動軸橫向幅值減小,輪軌接觸較為平緩,隨著輪軌激勵的不斷增加,橫向幅值逐漸增大。
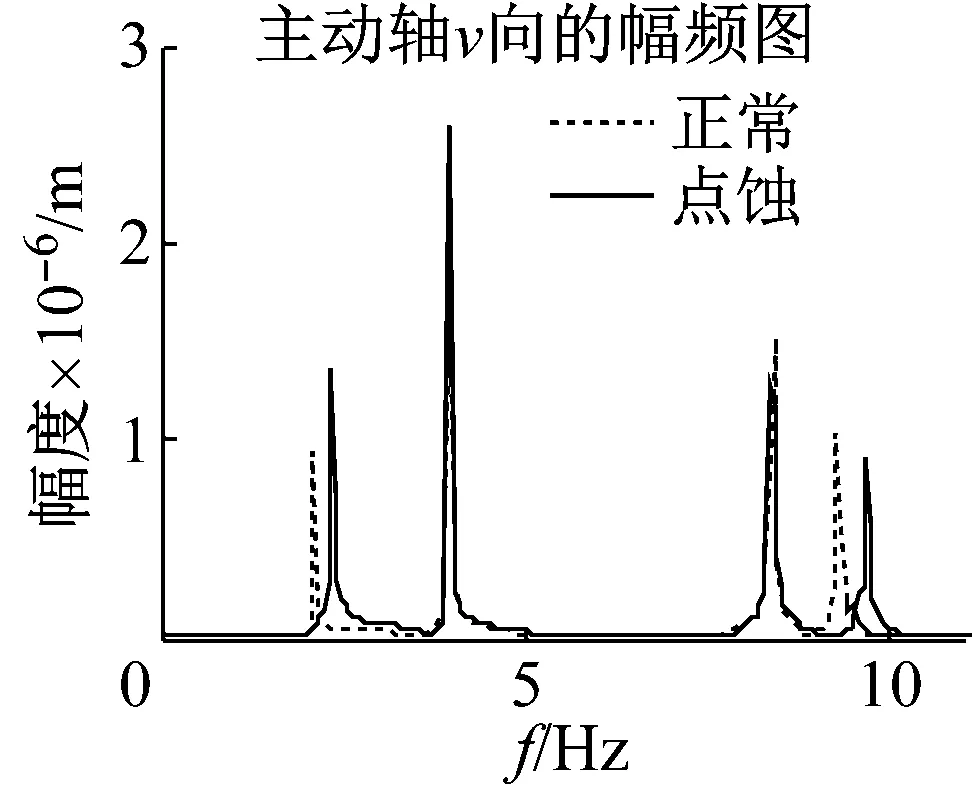
圖13 幅頻響應
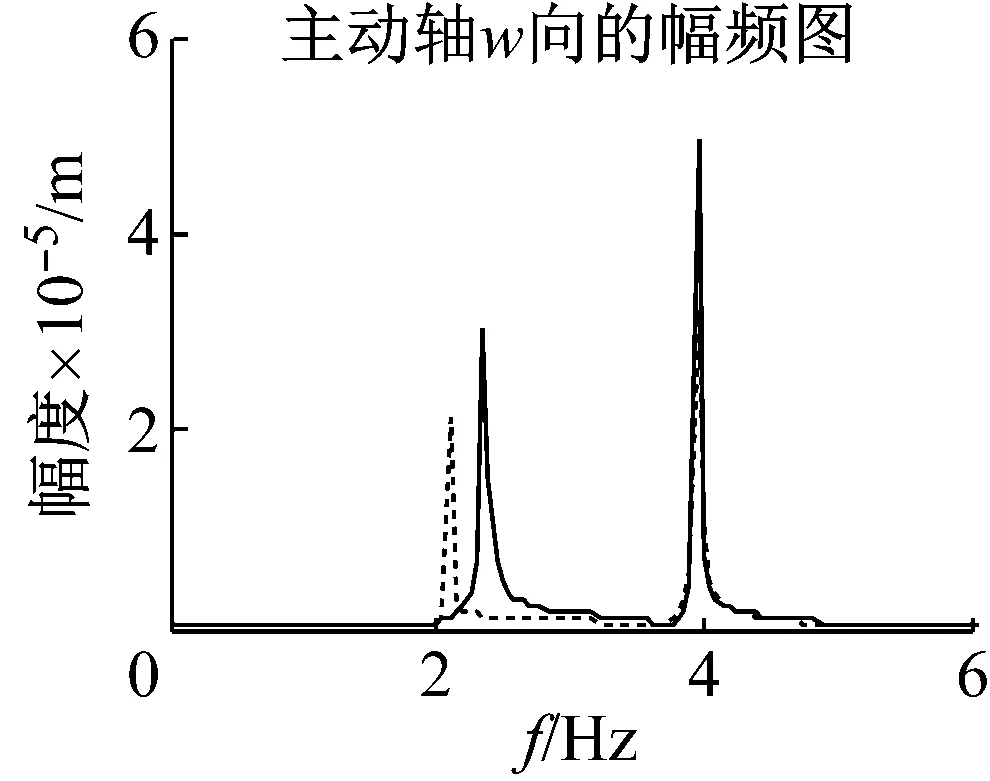
圖14 幅頻響應
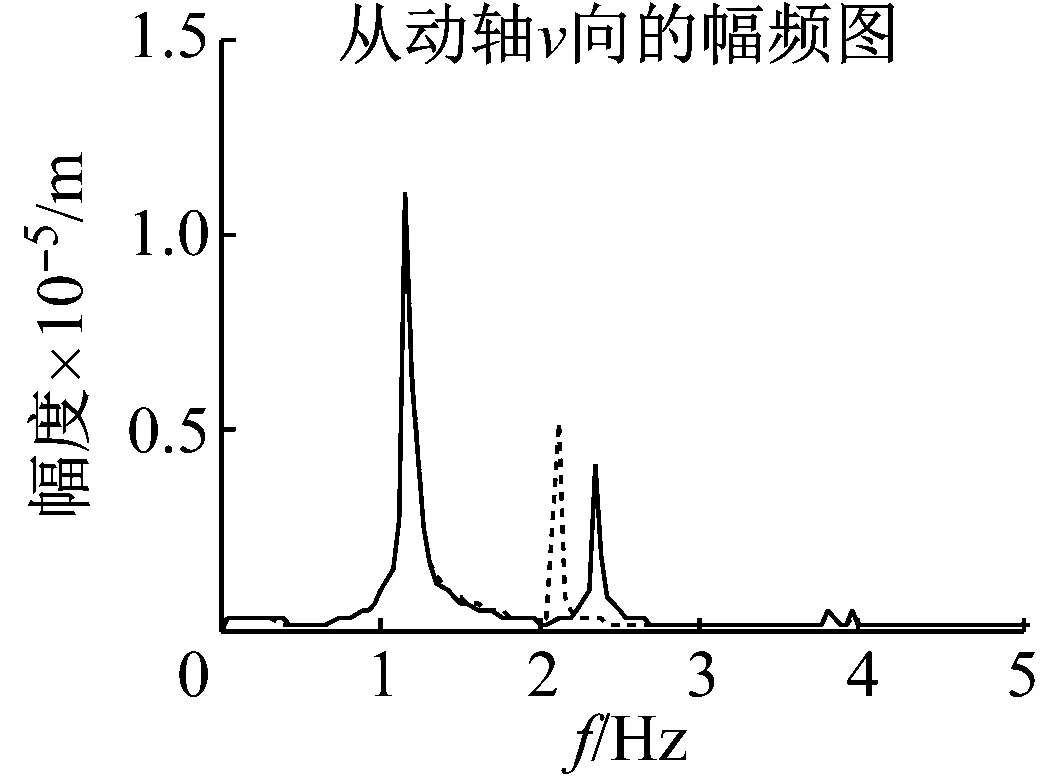
圖15 幅頻響應
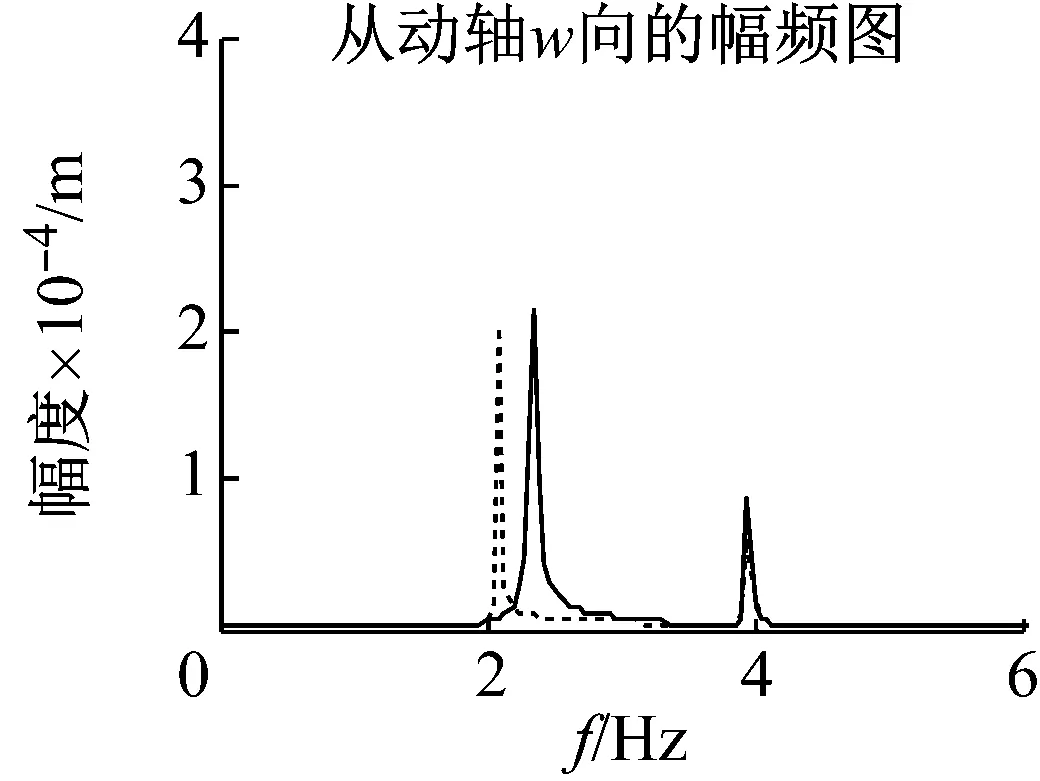
圖16 幅頻響應
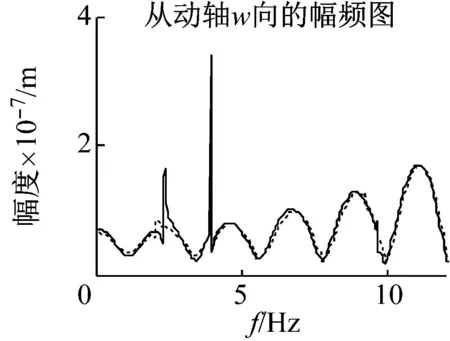
圖17 幅頻響應
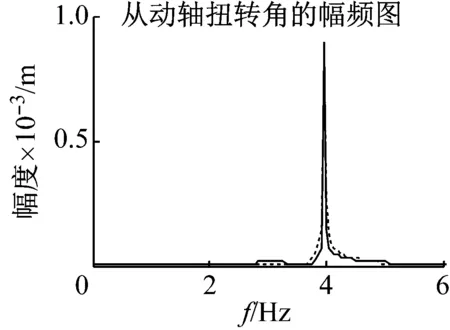
圖18 幅頻響應

圖19 輪軌激勵影響Fig.19 Wheel-rail excitation圖20 輪軌激勵影響Fig.20 Wheel-rail excitation
6 結 論
本文建立了連續質量軸轉子傳動系統彎扭耦合動力學模型,考慮了非線性齒輪嚙合剛度及輪軌接觸的影響。求解系統在復雜邊界條件下,轉子臨界轉速大小。計算與分析,得出轉子系統彎扭耦合的非線性振動特征及系統振動響應規律。
(1) 建立了連續轉子模型,能更好的分析輪對、軸、齒輪之間的相互關系及影響。
(2) 復合邊界條件下,精確求解轉子系統固有頻率方程,及其耦合模態值。
(3) 受齒輪嚙合剛度下,傳動系統縱向橫向彎曲幅值變化較為顯著,扭轉角在其耦合頻率幅值較大。點蝕作用下,一階固有頻率右移,主動軸響應值增大。
(4) 輪軌激勵P接觸耦合作用下,輪軌接觸力增大,從動軸橫向彎曲變化顯著。
總上,機車連續質量軸轉子系統模型,不同于傳統Jeffcott模型,對鐵路機車傳動系統動力學分析及齒輪軸承等故障分析提供了很好的動力學模型。

