讓學(xué)生“做”數(shù)學(xué)

劉金波

建構(gòu)主義認(rèn)知理論認(rèn)為，學(xué)習(xí)不應(yīng)被看成是對(duì)教師所講授的知識(shí)的被動(dòng)接受，而是學(xué)習(xí)者以自身已有的知識(shí)和經(jīng)驗(yàn)為基礎(chǔ)的主動(dòng)建構(gòu)活動(dòng)。數(shù)學(xué)學(xué)習(xí)更應(yīng)如此，因?yàn)閿?shù)學(xué)具有抽象性，學(xué)生理解起來不那么容易。為此，數(shù)學(xué)教學(xué)可通過典型例子的分析和學(xué)生的自主探索活動(dòng)，使學(xué)生理解數(shù)學(xué)知識(shí)形成的過程，體會(huì)其中蘊(yùn)含的思想方法，追尋數(shù)學(xué)發(fā)展的歷史足跡，把數(shù)學(xué)的學(xué)術(shù)形態(tài)轉(zhuǎn)化為學(xué)生易于接受的教育形態(tài)。這也就是我們所說的“做”數(shù)學(xué)，即數(shù)學(xué)教學(xué)形式由灌輸變?yōu)橹鲃?dòng)建構(gòu)。

例如，教學(xué)四邊形內(nèi)角和的度數(shù)時(shí)，教師首先提問：三角形內(nèi)角和為180毅，那么四邊形內(nèi)角和會(huì)是多少度？學(xué)生在獨(dú)立探索的基礎(chǔ)上分組交流與研討，并匯總解決問題的方法。

方法一：用量角器量出四個(gè)角的度數(shù)，然后把四個(gè)角加起來，發(fā)現(xiàn)內(nèi)角和是360毅。

方法二：用兩個(gè)相同的三角形紙板拼成一個(gè)四邊形，發(fā)現(xiàn)兩個(gè)三角形內(nèi)角和相加是360毅。

接下來，教師在方法二的基礎(chǔ)上引導(dǎo)學(xué)生利用作輔助線的方法，連結(jié)四邊形的對(duì)角線，把一個(gè)四邊形轉(zhuǎn)化成兩個(gè)三角形。小組交流后，學(xué)生運(yùn)用幾何畫板演示并驗(yàn)證得到的方法。

得到四邊形的內(nèi)角和是360毅之后，學(xué)生們又認(rèn)真地討論起五邊形、六邊形的內(nèi)角和。類比四邊形的討論方法，學(xué)生最終得出五邊形的內(nèi)角和是540毅，六邊形的內(nèi)角和是720毅。

這樣教學(xué)，學(xué)生在探究問題的過程中發(fā)現(xiàn)知識(shí)，經(jīng)歷數(shù)學(xué)知識(shí)的形成過程，從而得出結(jié)論，完成“做”數(shù)學(xué)的過程。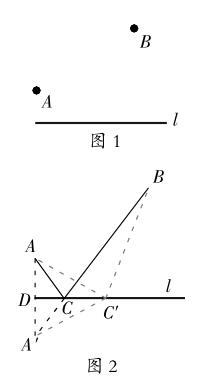

讓學(xué)生“做”數(shù)學(xué)，還包括學(xué)生會(huì)應(yīng)用數(shù)學(xué)知識(shí)解決實(shí)際問題。也就是說，我們既要讓學(xué)生知道數(shù)學(xué)知識(shí)從哪里來，又會(huì)到哪里去，即數(shù)學(xué)知識(shí)的應(yīng)用過程。因此，在數(shù)學(xué)教學(xué)中，教師還應(yīng)指導(dǎo)學(xué)生用數(shù)學(xué)的觀點(diǎn)觀察社會(huì)、思考問題，培養(yǎng)學(xué)生應(yīng)用數(shù)學(xué)的意識(shí)，真正做到學(xué)以致用。

例如，在復(fù)習(xí)軸對(duì)稱的知識(shí)時(shí)，教師不妨提出數(shù)學(xué)名題———將軍飲馬問題。

唐朝詩人李頎的詩《古從軍行》開頭兩句說：“白日登山望烽火，黃昏飲馬傍交河。”詩中隱含著一個(gè)有趣的數(shù)學(xué)問題。

如圖1所示，詩中將軍在觀望烽火之后從山腳下的A點(diǎn)出發(fā)，走到河邊飲馬后再回到B點(diǎn)宿營(yíng)。請(qǐng)問怎樣走才能使總的路程最短？

解決這個(gè)問題并不難，但要用到今天所學(xué)的軸對(duì)稱知識(shí)。如圖2所示，從A點(diǎn)出發(fā)向河岸引垂線，垂足為D，取A點(diǎn)關(guān)于河岸的對(duì)稱點(diǎn)A憶，連結(jié)A憶B，與河岸線l相交于C，則C點(diǎn)就是飲馬的地方。將軍只要從A點(diǎn)出發(fā)，沿直線走到C點(diǎn)，飲馬之后，再由C點(diǎn)沿直線走到B點(diǎn)，所走的路程就是最短的。

因?yàn)槿绻麑④娫诤舆叺牧硗馊我稽c(diǎn)C憶飲馬，所走的路程就是AC憶+C憶B，但是，AC憶+C憶B=A憶C憶+ C憶B>A憶B=A憶C+CB=AC+CB。

可見，在C點(diǎn)外任何一點(diǎn)C憶飲馬，所走的路程都要遠(yuǎn)一些。

這有幾點(diǎn)需要說明：（1）由作法可知，河流l相當(dāng)于線段AA憶的中垂線，所以AD=A憶D。（2）由上一條知：將軍走的路程就是AC+CB，就等于A憶C+ CB，而兩點(diǎn)確定一條直線，所以C點(diǎn)為最優(yōu)。這樣就將軸對(duì)稱知識(shí)用活了。

（作者單位：岳陽縣榮家灣鎮(zhèn)城關(guān)中心學(xué)校）