基于數值仿真的泵閥變剛度彈簧設計與優化

董世民，朱 葛

(燕山大學機械工程學院，秦皇島066004)

0 引 言

往復泵是一種通用的水力機械設備，在國民經濟的各個領域均得到了廣泛應用。泵閥是往復泵的重要部件，往復泵泵閥主要采用自動錐形閥結構。彈簧是自動錐形閥的重要組成部分，彈簧的主要作用是平衡慣性力，降低閥盤的落座速度與滯后高度，但是也降低了閥盤升程，增大了閥隙間的水頭損失，降低了吸入性能，因此彈簧對往復泵的工作性能影響明顯。國內外的許多專家學者在泵閥的工作理論、設計計算和應用方面進行了大量的研究工作[1-9]：阿道爾夫于1968年建立了泵閥運動規律的二階非線性常微分方程；針對阿道爾夫所建立泵閥運動微分方程在泵閥開啟瞬間存在奇點的問題，董世民等[7]綜合考慮流體可壓縮性與魏氏效應對泵筒與閥隙液體連續流方程的影響，建立了適用范圍更廣的泵閥運動規律仿真模型；基于泵閥運動規律的數值仿真方法，張慢來等[10-13]分析了彈簧剛度與預緊力對于泵閥運動特性的影響；鄭淑娟等[14-19]基于CFD流場可視化技術仿真分析了閥隙流場與閥出流特性；Pei等[20]基于臺架模擬試驗系統測試了泵閥運動規律。

彈簧剛度與預緊力等泵閥結構參數對泵閥動力特性有顯著影響，但目前的研究[10-19]僅限于單因素的仿真分析，基于優化設計理論的泵閥結構參數優化設計方法的研究尚不深入。例如，吳亮等[21-22]基于泵閥最大升程、最大滯后高度與落座沖擊速度的簡化解析模型給出了泵閥結構參數的簡化計算方法。目前，基于流體動力學仿真的優化設計技術已經廣泛應用流體機械結構的優化設計[23-26]。

目前往復泵錐閥結構與運動規律的研究都是針對定剛度彈簧的泵閥結構。結合非線性彈簧技術在改善機械系統動態特性領域的實際應用，筆者設計了變剛度系數彈簧的泵閥結構，以達到改善泵閥動力特性與泵吸入特性的目的。本文在建立變剛度彈簧泵閥運動規律仿真模型的基礎上，仿真分析變剛度彈簧對泵閥動力特性與泵吸入性能的綜合影響，進而建立基于系統動力仿真的變剛度彈簧參數的優化設計方法。

1 泵閥運動規律數學模型的建立

液缸內壓力過低時會引起液缸內出現明顯的空化現象，降低泵的充滿系數，同時泵出口處的流量脈動和壓力脈動大幅增加[27-29]，因此本文以吸入閥為研究對象，建立泵閥運動規律的數學模型，重點研究閥隙間的水頭損失和閥盤運動特性。為便于研究，做如下簡化和假設：1）忽略液體在液缸內流動時的沿程阻力損失；2）忽略連桿、活塞以及液缸等元件的彈性變形；3）假設液缸內的液體密度與壓力與液缸內的位置無關。

圖1與圖2分別為往復泵工作原理示意圖與往復泵錐閥結構示意圖。

1.1 閥盤運動微分方程

往復泵在吸液過程中，活塞由左死點向右運動，液缸內液體膨脹，壓力開始降低，當內外壓差足以克服彈簧預緊力與閥盤重力時，吸入閥開啟，此時閥盤分別受到以下幾個力的作用：閥盤下部與上部液體壓差作用下產生的舉升力、閥盤自身重力、彈簧彈力、液體對閥盤的水力阻力以及閥盤導向爪與閥座之間的摩擦力（摩擦力的作用方向與閥盤的運動速度方向相反），閥盤的運動微分方程為

式中 ms為閥盤質量，kg；p為液缸內液體壓力，Pa；ps為吸入管內吸入閥口處的液體壓力，Pa；fs為閥盤面積，m2；g為重力加速度，m/s2；k為彈簧剛度，N/m；h為閥盤升程，m；h0為彈簧預緊量，m；λ1為阻力系數；Rm為閥座對閥盤導向爪的摩擦力，N；sign(h)為符號函數，當h≥0時，sign(h)=1；當 h＜0時，sign(h)= -1；t為時間，s。

圖1 往復泵的工作原理圖Fig.1 Working principle diagram of reciprocating pump

圖2 自動錐形閥結構圖Fig.2 Structure diagram of automatic cone valve

目前，往復泵錐閥采用定剛度系數彈簧。若彈簧剛度系數隨彈簧變形量的變化而變化，則彈簧是變剛度系數彈簧。設彈簧剛度與彈簧變形量之間的函數關系為

式（1）中液體對閥盤的水力阻力、閥座對閥盤導向爪的摩擦力一般較小，忽略這兩項力的影響，吸入閥運動微分方程簡化為

1.2 泵閥閥隙連續流方程

根據單位時間內泵缸內流體質量的增量 dM1應等于經過泵閥閥隙流入泵缸的流體質量 dM2,即可建立流體連續性方程

其中單位時間內泵缸內流體質量的增量 dM1為

式中Fp為液缸內圓面積，m2；ρ為t時刻液缸內液體的密度，kg/m3；Vs為t時刻閥盤、閥隙與閥座所形成的空間體積且Vs=fsh，m3；xp為t時刻活塞的位移，m；x0為余隙長度，即將余隙容積轉化為橫截面為Fp的圓柱體所對應的長度，m。

液缸內的液體密度與壓力之間的函數關系為

式中ρ0為液缸內液體在標準下的密度，kg/m3；C0為液體的壓縮系數；p0為標準壓力，Pa。

活塞運動位移xp與速度vp可由式（7）、（8）確定。

式中λ為連桿比，其中λ=R/l；R為曲柄半徑，m；l為連桿長度，m。

單位時間內經過閥隙流入液缸內的液體質量為式中 μ 為流量系數；εs為系數，εs=±1；ρxs為經過閥隙流動液體的密度，kg/m3；fxs為閥隙的過流面積，m2。

當 Ps-P≥0 時，εs=1，ρxs=ρs（液體在吸入壓力 ps條件下的密度）；Ps-P＜0 時，εs=﹣1，ρxs=ρ。

其中閥隙的過流面積有

綜上推導可有

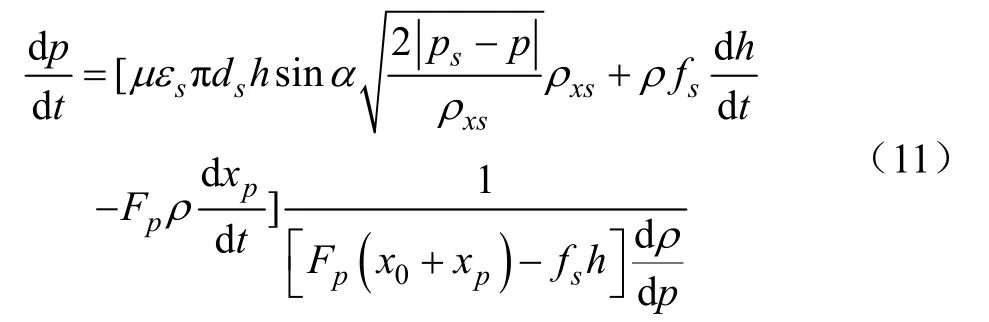
1.3 吸入閥運動初始條件的確定

由于滯后角的存在，活塞運動到左死點時，排出閥并未關閉，閥盤還存在一定的滯后高度，當排出閥關閉時，活塞由左死點向右走過的距離為xod,曲柄轉過的對應角度為ψod（排出閥的滯后關閉角）。隨著柱塞的繼續運動，泵缸內的壓強開始逐漸降低。當閥盤的上下壓差Δp產生的舉升力足以克服閥盤的重力與彈簧預緊力時，吸入閥開啟，由此可推導出泵閥的開啟壓差與開啟壓力為

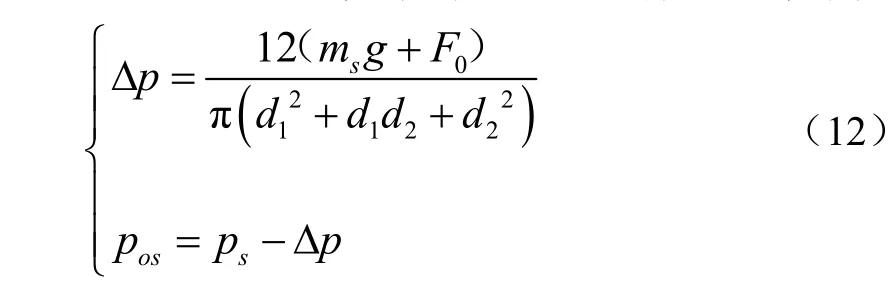
式中F0為彈簧預緊力，N；pos為吸入閥開啟瞬間對應的缸內壓力，Pa。

而彈簧預緊力F0與彈簧預壓量h0滿足如下的函數關系為

式中f(h0)是彈簧變形量為h0時對應的彈簧剛度。

根據泵缸內液體質量守恒可求得吸入閥打開瞬時的活塞位移xos為

式中 ρd為液體在排出壓力 Pd下的密度，kg/m3；ρos為液體在排出壓力pos下的密度，kg/m3。

根據活塞位移可求得吸入閥打開時刻ost滿足

式中tos為閥盤開啟瞬時對應的時間，s。吸入閥運動的初始條件為

1.4 吸入閥運動規律的數學模型

根據上述建立的吸入閥運動微分方程、泵閥連續流方程以及初始條件，建立了描述吸入閥運動規律的數學模型，可以寫成如下的一階常微分方程組

式中 x1為液缸內液體壓力，Pa；x2為泵閥升程，m；x3為閥盤的運動速度，m/s。

根據液缸內液體瞬時壓力的仿真結果，計算吸入閥吸液過程中閥隙間的最大水頭損失為

2 泵閥運動規律的仿真計算

2.1 仿真模型精度驗證

根據上述建立的彈簧變剛度系數條件下泵閥運動規律的數學模型，本文采用龍格—庫塔法建立了泵閥運動規律的仿真模型，并基于Matlab開發了泵閥運動規律仿真程序。為了驗證仿真模型的計算精度，利用該程序對油田3NB-1300型鉆井往復泵進行了仿真試驗，該泵的仿真試驗參數為：沖程0.254 m，液缸直徑0.170 m，鉆井液密度1 100 kg/m3，閥盤質量為4.0 kg，彈簧為普通圓柱螺旋彈簧，剛度系數7 500 N/m，預緊力230 N。

仿真過程中，給定工況參數：排出壓力Pd為0.16 MPa，吸入壓力Ps為0.13 MPa，沖次為74 min-1。根據式（12）、（14）以及（15）求出吸入閥開啟瞬間對應的液缸內壓力Pos等初始條件，代入上述建立的泵閥運動規律仿真程序，得到該泵沖次為74 min-1時的閥盤升程、運動速度以及液缸內壓力隨曲柄轉角變化規律的仿真曲線，結果如圖3所示。

實際測量過程中，使3NB-1300型鉆井往復泵在相同工況條件下運轉，使用半導體應變片壓力傳感器測定液缸內與吸入管內壓力，采用閥位移傳感器測量閥盤位移，使用自制的測死點裝置獲得柱塞左、右死點位置，得到吸入閥開啟過程中不同轉角下閥盤升程的實測結果[7]，與仿真結果對比如圖3所示。

圖3 74 min-1沖次閥盤升程、運動速度與液缸內壓力曲線Fig.3 Curve of valve disc lift, movement velocity and pressure in liquid cylinder under stroke frequency of 74 min-1

為了進一步驗證不同工況條件下仿真模型的計算精度，僅改變沖次參數，分別提取不同沖次下閥盤最大升程仿真結果與實測結果[7]進行對比，如表1所示。

表1 泵閥最大升程仿真結果與實測結果對比Table 1 Comparison between simulation results and measured results about maximum lift

由圖3可見，泵閥升程的仿真曲線與實測結果比較吻合，仿真誤差小于±8%；對比表1中的仿真結果與實測結果，泵閥的最大升程仿真誤差小于±10%，說明上述建立的描述泵閥運動規律的仿真模型基本滿足工程實際的精度要求。

2.2 不同彈簧類型泵閥運動規律及吸入性能仿真對比

2.2.1 定剛度系數彈簧仿真試驗

圖 4為使用定剛度系數彈簧時，不同預緊力與剛度組合條件下閥隙間最大水頭損失、滯后高度與閥盤落座速度的仿真圖像。

圖4 定剛度系數彈簧時泵閥性能仿真結果圖4 Simulation results of pump valve performance under constant stiffness coefficient condition

由圖4可以得出以下結論：

1）對于定剛度系數彈簧，吸液過程中閥隙間最大水頭損失隨預緊力與剛度的增大而增大，閥盤落座速度與滯后高度隨預緊力與剛度的增大而減小；

2）在所有仿真實例中當F0=100 N，k=1 000 N/m時，流體流經閥隙的最大水頭損失最小，僅為1.372 2 m，但此時閥盤的落座速度與滯后關閉高度達到最大；相反當F0=300 N，k=100 000 N/m時，閥盤的落座速度與滯后高度最小，但閥隙最大水頭損失最大，達到9.590 9 m。

綜上可以看出，閥隙間水頭損失與落座速度以及滯后高度的變化趨勢相互矛盾，即對于定剛度系數彈簧，很難通過單純的調節剛度與預緊力的方式達到既降低水頭損失又降低落座速度與滯后高度的目的。

2.2.2 變剛度系數彈簧仿真試驗

當泵閥采用變剛度彈簧時，吸入過程中液缸內的最低吸入壓力、泵閥最大升程、泵閥滯后高度以及泵閥落座沖擊速度都是彈簧剛度函數的函數，即都是彈簧剛度函數的泛函。為便于仿真分析以及優化及建模，將彈簧剛度函數式（2）簡化為

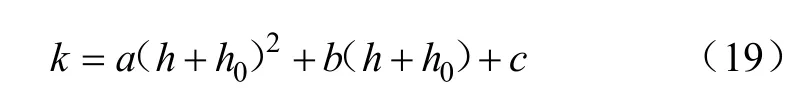
式中a，b，c為常數。

彈簧恢復力與變形量之間的關系可分為以下 3種類型：直線型、漸增型、漸減型。式（19）中，取系數a，b，c的不同組合便可以得到不同類型的彈簧。以下對比仿真不同類型彈簧泵閥的運動參數與閥隙水頭損失。仿真計算的彈簧類型以及有關系數見表2，仿真結果如圖5所示。

表2 不同彈簧類型仿真參數Table 2 Simulation parameters of different spring types

圖5 不同彈簧類型泵閥性能對比Fig.5 Pump valve performance comparison among different spring type

通過以上對不同類型彈簧的仿真試驗可以看出： 1）閥盤的落座速度與滯后高度一定時，對比閥隙間的水頭損失，漸減型彈簧的最大水頭損失最小，吸入性能最好，且在泵閥開啟后，漸減型彈簧的水頭損失穩定，對于減小液缸內的壓力波動也具有一定的作用；2）發現漸減型彈簧的閥盤開啟過程中速度較大，開啟后的最大升程最大，升程曲線與坐標軸所夾面積最大，有利于降低整個吸液過程中總的水頭損失。

3 泵閥變剛度系數彈簧參數優化

由上述仿真結果可知，變剛度系數彈簧對于改善往復泵的工作性能確有一定的作用，下面將基于仿真優化的思想對變剛度彈簧系數進行優化設計。

3.1 設計變量

根據式（19）確定的彈簧剛度與變形量之間的對應函數關系，其中系數a，b，c對于剛度的變化趨勢影響明顯。此外，常剛度系數彈簧的剛度近似認為恒定，預緊量確定后，預緊力在整個工作過程中不變，但是在變剛度系數條件下，隨著彈簧剛度的變化，預緊力部分也隨之發生變化，因此對變剛度彈簧進行優化設計時，選取了式（19）中的系數a，b，c以及彈簧的預緊量h0進行優化。

3.2 目標函數

在吸入條件不變的情況下，即吸入口壓力恒定時，流體流經閥隙時的水頭損失越大，缸內的壓力越低，當缸內壓力低于流體的空氣分離壓力或飽和蒸氣壓時，就有可能引發空化，使往復泵的充滿系數降低，影響往復泵的工作性能。因此本次優化選取吸入閥閥隙間的最大水頭損失為目標函數。

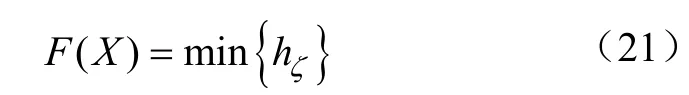
3.3 約束條件

泵閥的質量和它的關閉速度會形成機械動能，在泵閥關閉的瞬間會對閥座造成沖擊，由于泵閥經常處于啟閉交替地工作狀態，啟閉比較頻繁，因此，在泵閥設計中除了要滿足靜壓下的強度校核，還要特別注意泵閥的關閉速度。根據阿道爾夫無沖擊理論，當閥盤的落座速度小于允許關閉速度時，就可近似認為不產生沖擊，即對閥盤的使用壽命影響不明顯[30]。所以，控制閥盤的允許關閉速度對泵閥設計至關重要，其中泵閥的允許關閉速度是根據阿道爾夫的試驗結果最終確定的，即

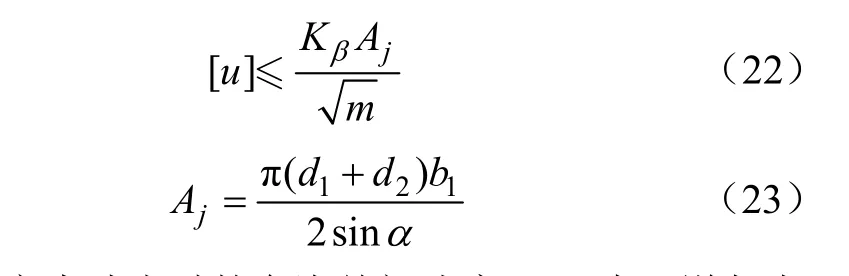
式中[u]為不產生沖擊時的允許關閉速度；Kβ為阿道爾夫試驗系數；Aj閥盤與閥座接觸面積；m閥盤質量；d1為閥盤直徑；d2為閥座孔直徑；α為閥盤錐角；b1為閥座壁厚。

此外，彈簧預緊量、預緊力以及閥盤升程最大時的彈簧力必須為正值因此約束條件即為

綜合上述目標函數和約束條件，基于數值仿真的變剛度彈簧參數優化設計數學模型為

3.4 仿真與優化實例

使用2.1中的仿真參數，計算[u]時，取阿道爾夫試驗系數 Kβ=1.30，b1=0.5 cm,由式（23）計算出 Aj=20.2 cm2，由式（22）可以計算出泵閥的允許關閉速度[u]=10.1 cm/s。調用仿真優化程序，采用遺傳算法與模式搜索綜合的智能優化算法進行求解，將優化結果與傳統設計方案中的常剛度系數彈簧進行對比，對比結果如表 3所示，圖 6為優化后的變剛度彈簧與定剛度彈簧泵閥性能對比曲線。

表3 變剛度系數彈簧優化結果與定剛度系數彈簧性能對比Table 3 Comparison of variable stiffness spring optimization results constant stiffness coefficient spring

由以上的仿真曲線可以看出，在限定閥盤的落座速度滿足無沖擊條件時，優化后閥隙間的水頭損失明顯降低，其中最大水頭損失遠低于定剛度系數彈簧。由表 3可以看出，與使用傳統設計方法確定的定剛度系數彈簧泵閥相比，使用變剛度系數彈簧后，閥隙間最大水頭損失降低幅度達到了20.85%，即液缸內壓力得到顯著提升，對于避免液缸內流體發生空化，提高往復泵的吸入性能具有重要意義。

圖6 優化后泵閥性能對比Fig.6 Pump valve performance comparison after optimization

4 結論與討論

本文建立了彈簧變剛度系數條件下泵閥運動規律的數學模型，分別比較了定剛度系數彈簧與變剛度系數彈簧對泵閥性能的影響，并提出了基于數值仿真的變剛度系數彈簧參數優化方法，對變剛度系數彈簧進行了優化設計，得到如下結論：

1）漸減型變剛度系數彈簧可以在不增加落座速度與滯后關閉高度的同時，降低閥隙間的最大水頭損失，提高往復泵的吸入性能。

2）優化后，在滿足無沖擊條件下，閥隙間最大水頭損失降低了20.85%，說明變剛度系數彈簧在往復泵泵閥上的應用具有一定的工程實際意義。

針對優化后變剛度系數彈簧與定剛度系數彈簧對泵閥性能的影響，本文僅就數值仿真結果進行了初步對比，具體試驗驗證部分還需進一步完善。